2. 南京信息工程大学 江苏省大数据分析技术重点实验室, 江苏 南京 210044
2. Jiangsu Key Laboratory of Big Data Analysis Technology/B-DAT, Nanjing University of Information Science & Technology, Nanjing 210044, China
属性约简是Rough集理论中的核心问题之一,也是知识获取的关键步骤。目前,许多学者已提出了一些有效的属性约简算法[1-4],如基于正区域的属性约简算法、基于差别矩阵的属性约简算法、基于信息熵的属性约简算法等,但这些算法都是针对静态的决策表,不适合处理动态的信息系统。现实世界是不断变化的,数据会源源不断地添加到原始决策表中,一般不希望将原有的决策表和新产生的增量数据整合成一个新的决策表进行属性约简,因为这样会对原有数据不断地进行重复的计算。因此,如何利用原决策表中所含的信息并结合增量数据来进行属性约简成为粗糙集理论新的挑战。
数据的动态变化主要有3种情况:1)属性集保持不变而对象不断增加[5-8];2)对象集保持不变而属性集不断增加[9];3)对象集和属性集同时增加[10]。本文着重研究第1种情况的增量式属性约简问题,尤其研究适合大规模数据集的约简问题。文献[5]提出了基于正区域的属性约简增量式更新算法,提高了属性约简算法效率;文献[6]提出了基于差别矩阵的属性约简增量式更新算法;文献[7]提出了不使用可辨识矩阵的增量式核更新算法以及属性约简算法;文献[8]针对现有增量式属性约简算法中存在的约简传承性差以及不完备现象,提出了基于标记可辨识矩阵的增量式属性约简算法。然而,这些算法不适宜解决每次增加批量对象的问题。文献[11]提出了面向成组对象集的3种增量式信息熵属性约简算法;文献[12]充分利用先前约简中信息和计数排序算法快速更新批量对象的约简,降低计算复杂度;文献[13-14]探讨了混合属性约简算法以及利用MapReduce进行面向大规模数据集的属性约简方法。
为提高增量式学习算法效率[15]和约简传承性,本文构建了面向成组对象的增量式属性约简算法,利用原始决策表的一个候选约简来快速地更新新增决策表的约简,这样既提高了约简的传承性,又有效地利用了原有知识,提高了增量式学习算法效率。
1 粗糙集概念下面简要介绍本文主要用到的一些Rough集的基本概念[1, 9, 11, 13-14]。
定义1 四元组S=<U,C∪D,V,f>是一个决策表,其中U={x1,x2,…,xn}表示对象的非空有限集合,称为论域;C表示条件属性的非空有限集,D表示决策属性的非空有限集,C∩D=Ø;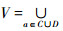
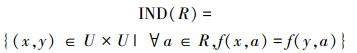 |
关系IND(R)构成了U的一个划分,用U/IND(R)表示,简记为U/R。U/R中的任何元素[x]R={y| ∀a∈R,f(x,a)=f(y,a)}称为等价类。不失一般性,假设决策表S仅有一个决策属性D={d},其决策属性值映射为1,2,…,k,由D导出的U上划分记为U/D={D1,D2,…,Dk},其中,Di={x∈U| f(x,D)=i},i=1,2,…,k。
定义2 在决策表S=<U,C∪D,V,f>中,对于每个决策类Di∈U/D和不可区分关系A⊆C,Di的下近似集与上近似集分别可以由A的基本集定义如下:
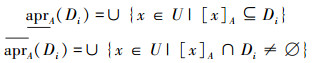 |
定义3 在决策表S=<U,C,D,V,f>中,∀A⊆C,正区域POSA(D)和边界域BNDA(D)定义为
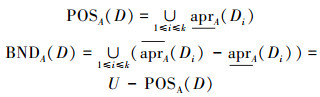 |
定义4 在决策表S中,一个属性集Red⊆C是C的D-约简,如果
1)POSRed(D)=POSC(D);
2)∀a∈Red,POSRed-{a}(D)≠POSRed(D)。
定义5 在决策表S中,A⊆C,∀c∈A,在正区域下属性c重要性定义为
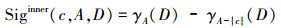 |
式中: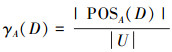
定义6 在决策表S中,A⊆C,∀c∈C-A,在正区域下属性c重要性定义为
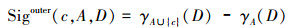 |
定义7 设Red为决策表S的候选属性约简,NewRed为新增样本之后的新约简,则单次增量式约简的传承率(inheritance rate,IR)定义为
 |
假设进行了w次增量式约简,则平均传承率(inheritance rate average,IRA)定义为
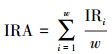 |
在约简过程中,传承率越高则约简集的变化越小,对原始规则集的影响将越小。如果传承率为1,说明新增的对象不影响原始的规则集;如果传承率为0,则新的约简集与原来的约简集完全不同,这时需全部更新所有规则。
2 面向成组对象集的增量式属性约简算法给定决策表S=<U,C∪D,V,f>,一个约简Red⊆C。新对象y加入到决策表S中,U′=U∪{y},将此时的新决策表标记为S′。一种最简单的属性约简增量式更新算法是直接计算S′的约简。显然,这种方法的属性约简效率比较低下,因为需要重复计算原始决策表S中的等价类。为此,如何在已有的约简Red的基础上快速更新约简则成为本文主要研究内容。为此,如何在已有的约简Red的基础上快速更新约简则成为本文主要研究内容。为方便讨论,假设U/Red={X1,X2,…,Xm},U/C={X′1,X′2,…,X′t},用POSRedU表示决策表S由约简Red导出的正区域,用BNDRedU表示决策表S由约简Red导出的边界域,即U-POSRedU。
当新对象y加入到S中,主要分为两类情况:
1)y无法用Red区分,当且仅当∃x∈U使得∀a∈Red[f(x,a)=f(y,a)];
2)y可以用Red区分,当且仅当∀x∈U使得∃a∈Red[f(x,a)≠f(y,a)]。
对于第2种情况,显然POSRedU′= POSRedU∪{y},则Red是新决策表S′的约简。对于第1种情况,还不能完全判断出正区域的变化,需要对上述情况进一步细分,分为以下4种情况。
①若∃Xi∈BNDCU[y∈Xi],则POSRedU′= POSCU′;
②若∃Xi∈POSCU[y∈Xi],分为2种情况:a) ∀x∈Xi[f(x,d)=f(y,d)],则POSRedU′= POSRedU∪ {y},而POSCU′=POSCU∪ {y},即POSRedU′=POSCU′;b)∃x∈Xi [f(x,d)≠f(y,d)],则POSCU′= POSCU - Xi,而POSRedU′= POSRedU - Xi,则POSCU′=POSRedU′。总之,POSRedU′= POSCU′。
③若[y]C∉U/C∧[y]Red∈U/Red,若∃x∈POSRedU使得∀z∈[x]Red[f(z,d)=f(y,d)],则POSRedU′= POSRedU∪{y} ,而POSCU′= POSCU∪{y},则POSRedU′=POSCU′;
④当[y]C∉U/C∧[y]Red∈U/Red,若∃x∈POSRedU使得∃z∈[x]Red [f(x,d)≠f(y,d)],则POSRedU′=POSRedU- [x]Red,而POSCU′=POSCU∪{y},即POSRedU′≠ POSCU′。
根据上述分析,可以得出以下定理。
定理1 给定决策表S和新增对象y,Red是决策表S的约简,若∃Xi∈BNDCU[y∈Xi],则Red是新决策表S′的约简。
证明 若Red为决策表S的约简,则POSRedU=POSCU。又∃Xi∈BNDCU[y∈Xi],则POSCU′=POSCU和POSRedU′=POSRedU,从而POSCU′=POSRedU′,故Red为决策表S′的约简。
定理2 给定决策表S和新增对象y,Red是决策表S的约简,若∃Xi∈POSCU[y∈Xi]且∀z∈Xi[∀a∈Red[f(z,a)=f(y,a)]⇒f(z,d)=f(y,d)],则Red是新决策表S′的约简。
证明 若Red为决策表S的约简,则POSRedU=POSCU。又∃Xi∈POSRedU[y∈Xi]且∀z∈Xi[∀a∈Red[f(z,a)=f(y,a)⇒f(z,d)=f(y,d)],则POSCU′=POSCU∪{y}和POSRedU′=POSRedU∪ {y},从而 POSRedU′= POSCU′,故Red为决策表S′的约简。
定理3 给定决策表S和新增对象y,Red是决策表S的约简,y∉U/C∧y∈U/Red,若∃z∈Xi[f(z,Red)=f(y,Red)]∧f(z,d)≠f(y,d),则Red不是决策表S′的约简。
证明 若Red为决策表S的约简,则POSRedU=POSCU。又y∉U/C,则POSCU′=POSCU∪{y}。[y]Red∈U/Red,若∃z∈Xi[f(x,Red)=f(y,Red)] ∧f(x,d)≠f(y,d),显然POSRedU′≠ POSRedU∪{y},故Red不是决策表S′的约简。
下面给出面向单个对象的增量式属性约简算法,如算法1所示。
算法1 面向单个对象的增量式属性约简算法
输入 一个决策表,S;一个新增对象,y;一个约简,RedU;
输出 一个新的约简,RedU∪{y}。
1)A=RedU;
2)计算U/A={A1,A2,…,Ar},U/C={X1,X2,…,Xt},计算POSCU和POSAU//y属于旧的正区域
3)如果y∈POSCU,则转到9);//y属于旧的边界域
4)如果y∈BNDCU,则转到9);//y属于新的正区域对象
5)如果y∉U/A,则转到9);否则A′h=Ah∪{y};
6)判断A′h 一致性,若A′h中对象的决策一致,则转到9);//y与其他对象在A属性集上产生冲突
7)While (|POSAA′h|≠|POSCA′h|)
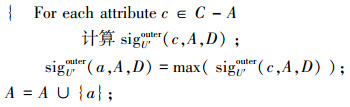 |
8) For each attribute c∈A
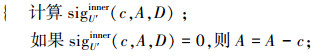 |
9)RedU∪{y}=A,输出RedU∪{y}。
复杂度分析 算法的时间复杂度主要集中在2)、7)和8)。利用文献[13]中计数排序算法和简化决策表处理方式,2)的时间复杂度为O(|C||U|),7)的时间复杂度为O(|C||U|),8)的最坏时间复杂度为O(|C|2(|U/C|+1)),故整个算法时间复杂度为max(O(|C||U|),O(|C|2(|U/C|+1)),空间复杂度为O(|U|)。
若每次只增加一个对象,使用算法1来计算约简,其计算效率较差。为此,本文主要考虑当每次增加一批对象时如何进行属性约简。给定一个决策表S,A⊆C,U/A={A1,A2,…,Ar}。假设U△是新增的对象集,U△/A={A1△,A2△,…,Ar′△},那么(U∪U△)/A={A′1,A′2,…,A′h,Ah+1,…,Ar,Ah+1△,…,Ar′△},其中A′i=Ai∪Ai△(i=1,2,…,h)。当成批增加对象时,我们主要考虑U∪U△中A不能区分的对象集,进一步说就是考虑A′i中对象集以及Ah+1△,…,Ar′△中C能够区分而A不能区分的对象集。下面给出面向成组对象集的增量式属性约简算法,如算法2所示。
算法2 面向成组对象集的增量式属性约简算法(GIAR)
输入 一个决策表,S;一个候选约简,RedU;新增对象集,U△;
输出 一个新的约简,RedU∪U△。
1)A=RedU,U′bnd=Ø;
2)计算 U/A={A1,A2,…,Ar},U△/A={A1△,A2△,…,Ar′△}和(U∪U△)/A={A′1,A′2,…,A′h,Ah+1,…,Ar,Ah+1△,…,Ar′△};
3)U/C={X1,X2,…,Xt},U△/C={X1△ ,X2△,…,Xt′△}和(U∪U△)/C={X′1,X′2,…,X′h′,Xh′+1,…,Xr,Xh′+1△,…,Xt′△};
4)如果h=0 和h′=0,转5;
5)计算POSAU△和POSCU△,如果POSAU△=POSCU△,转到10);否则转到6)。//新增对象集中约简不能区分的矛盾对象
6)U′bnd=UΔ - POSAU△;
7)for i=1 to h {如果A′i不一致,则U′bnd=U′bnd∪A′i;}//累加同一等价类中约简不能区分的矛盾对象
8)计算POSAU′bnd和POSCU′bnd;
9)While (|POSAU′bnd| ≠|POSCU′bnd|)
 |
//若这样的属性有多个,则任选一个;A=A ∪ {a};}
10)For each attribute c∈A
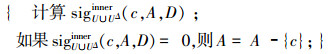 |
11)RedU∪U△=A,输出RedU∪U△。
复杂度分析 算法的时间复杂度主要集中在2)、3)、9)和10)。利用文献[13]中计数排序算法和简化决策表处理方式,2)的时间复杂度为O(|A||U∪UΔ|),3)的时间复杂度为O(|C||U∪UΔ|),9)的时间复杂度为O(|C||U′bnd|),10)的最坏时间复杂度为O(|C|2|[U∪UΔ]/C|),故整个算法时间复杂度为max(O(|C||U′bnd|),O(|C|2|[U∪UΔ]/C|)),空间复杂度为O(|U∪UΔ|)。
例1 表 1给出一个决策表S和新增对象集U△,决策表S包含3个约简{c2c1}、{c2c3}和{c3c4},分别计算约简的变化情况,如表 2所示。
| U | c1 | c2 | c3 | c4 | d | U△ | c1 | c2 | c3 | c4 | d |
| x1 | 1 | 0 | 1 | 0 | 2 | y1 | 2 | 1 | 0 | 0 | 1 |
| x2 | 0 | 1 | 0 | 1 | 2 | y2 | 1 | 0 | 1 | 0 | 4 |
| x3 | 1 | 1 | 1 | 1 | 3 | y3 | 0 | 1 | 0 | 1 | 2 |
| x4 | 1 | 0 | 1 | 0 | 1 | y4 | 0 | 2 | 1 | 1 | 1 |
| x5 | 0 | 2 | 2 | 1 | 2 | y5 | 0 | 1 | 1 | 1 | 2 |
| x6 | 1 | 2 | 0 | 0 | 2 | y6 | 0 | 1 | 1 | 2 | 1 |
| NewObject | Case | RedU | RedU′ | IR | RedU | RedU′ | IR | RedU | RedU′ | IR |
| 21001 | 1) | c2c1 | c2c1 | 1 | c2c3 | c2c1 | 0.5 | c3c4 | c3c4c1 | 1 |
| 10104 | ① | c2c1 | c2c1 | 1 | c2c3 | c2c3 | 1 | c3c4 | c3c4 | 1 |
| 01012 | ② | c2c1 | c2c1 | 1 | c2c3 | c2c3 | 1 | c3c4 | c3c4 | 1 |
| 02111 | ② | c2c1 | c2c1 | 1 | c2c3 | c2c3 | 1 | c3c4 | c3c4c1 | 1 |
| 01112 | ③ | c2c1 | c2c1 | 1 | c2c3 | c2c1 | 0.5 | c3c4 | c3c4c1 | 1 |
| 01121 | ④ | c2c1 | c2c1c3 | 1 | c2c3 | c2c3c1 | 1 | c3c4 | c3c4 | 1 |
| 合计 | 平均传承率 | 1 | 平均传承率 | 0.83 | 平均传承率 | 1 | ||||
3 实验验证
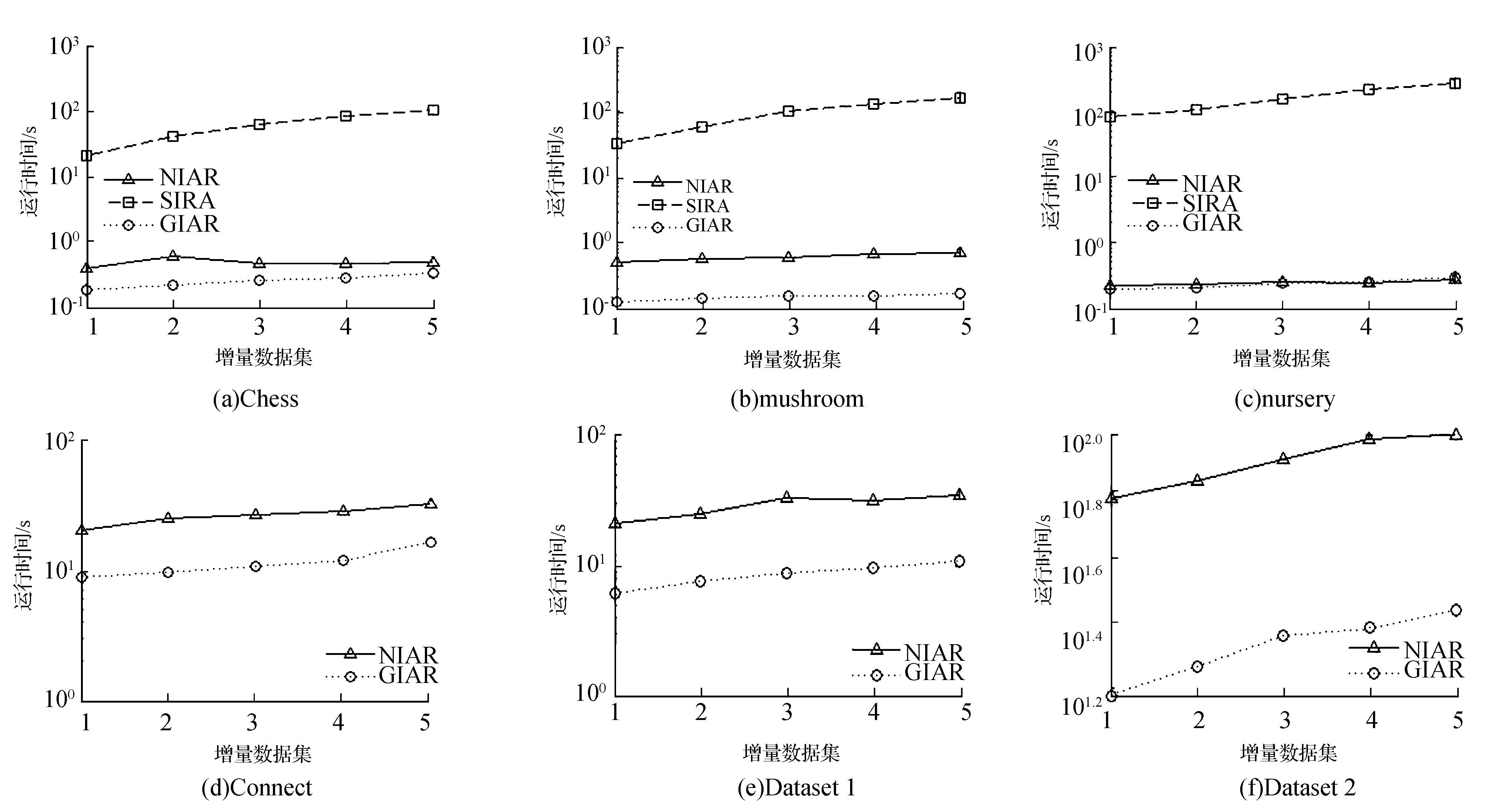
为了评价所提出的增量式约简算法效率和约简传承性,使用Windows 7操作系统,2.4GHz处理器和16GB内存的计算机和Visual C#2012实现了相关实验。由于所提出的约简算法和经典的约简算法仅能够处理离散型属性,先采用Rosetta软件(http://www.lcb.uu.se/tools/rosetta)填充缺省值,并将数值型属性连续值离散化;然后,分别在4个来自UCI Repository机器学习公共数据集和2个人工数据集进行实验。每个数据集仅有1个决策属性。人工数据集Dataset1每个属性值为1~5;而人工数据集Dataset2每个属性值为1~9。表 3描述了6个数据集特性。原始数据集的50%作为基本数据集,剩下50%数据集的20%、40%、60%、80%和100%作为5个增量数据集,非增量式属性约简算法(NIAR)、面向单个属性的增量式属性约简算法(SIAR)和面向成组数据集的属性增量式约简算法(GIAR)实验结果如图 1所示。
|
| 图 1 增量式约简算法和非增量式约简算法运行时间比较 Fig. 1 Comparison of incremental and non-incremental Reduction algorithms on running time |
| 序号 | 数据集 | 对象数 | 属性个数 | 类别数 |
| 1 | Chess | 3 196 | 36 | 2 |
| 2 | mushroom | 8 124 | 22 | 2 |
| 3 | nursery | 12 960 | 9 | 5 |
| 4 | Connect | 67 557 | 42 | 3 |
| 5 | Dataset1 | 200 000 | 30 | 5 |
| 6 | Dataset2 | 500 000 | 30 | 9 |
由于面向单个属性的增量式约简算法(SIAR)对大规模数据集运行时间太长,图 1(e)-(f)未标出。从图 1可以看出,SIAR算法比GIAR算法运行时间更长,而GIAR算法的运行时间明显少于NIAR算法,特别对于较大数据集,算法的效果越明显。实验结果表明,所提出的面向成组对象集的增量式约简算法是可行的。
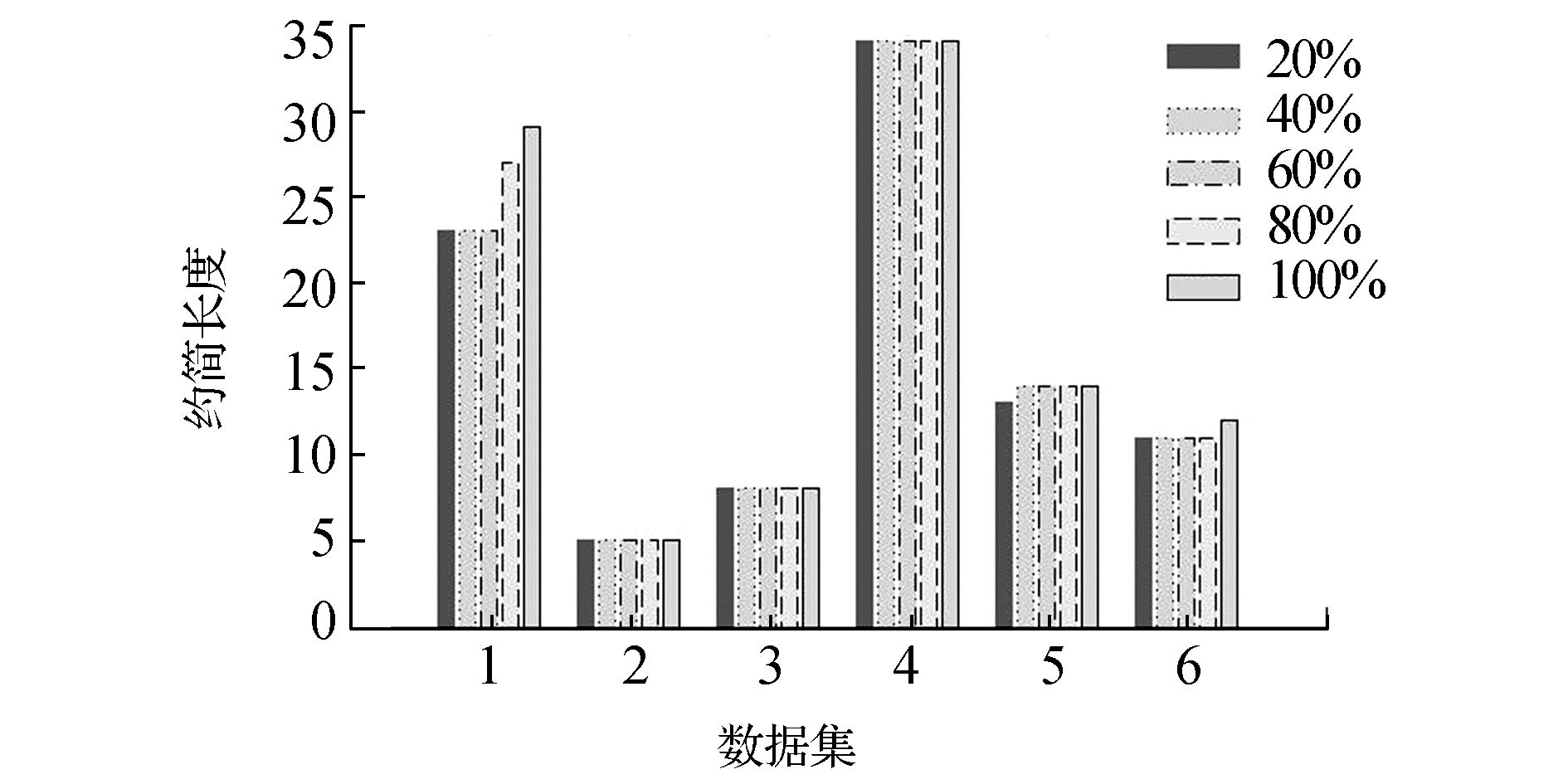
下面比较约简长度与约简的传承性。图 2给出了6个数据集在不同增长比例下的约简长度。在4个数据集上,约简不变,则只需要生成新增数据集的规则,原始规则集不必重新生成,而在另外两个数据集上,约简长度稍微增长,这主要因为新增对象与原始数据集引起冲突,需要另外的属性集来细分原始对象,这时除了生成新规则集外,还需要修改部分原始规则。
|
| 图 2 约简长度比较 Fig. 2 Comparison of Reduct length |
表 4给出了约简的传承性。从表 4可以看出,利用先前约简中信息所得到的新约简结果变化不大,约简传承性较好。
| % | |||||
| 数据集 | 20% | 40% | 60% | 80% | 100% |
| Chess | 100 | 100 | 95.45 | 95.45 | 95.45 |
| mushroom | 100 | 100 | 100 | 100 | 100 |
| nursery | 100 | 100 | 100 | 100 | 100 |
| Connect | 100 | 100 | 100 | 100 | 100 |
| Dataset1 | 100 | 100 | 100 | 100 | 100 |
| Dataset2 | 100 | 100 | 90.9 | 90.9 | 100 |
4 结论
在数据挖掘中,属性约简仅仅是数据预处理中一个过程,挖掘规则才是最终的输出。因此,充分利用先前约简中信息不仅能够快速得到约简,而且更容易地利用已有知识进行规则更新。本文所提出的面向成组对象集的增量式约简方法就是充分利用先前约简中信息来快速更新约简,不仅具有较高的约简传承率,而且可以快速进行增量式学习,具有良好的实用性。作者下一步将利用MapReduce进一步研究大规模数据集增量式属性约简方法。
| [1] | PAWLAK Z. Rough sets[J]. International journal of computer & information sciences , 1982, 11 (5) : 341-356 |
| [2] | SKOWRON A, RAUSZER C. The discernibility matrices and functions in information systems[M]//SLOWINSKI R. Intelligent Decision Support, Handbook of Applications and Advances of the Rough Sets Theory. Netherlands:Springer, 1992:311-362. |
| [3] | 苗夺谦, 胡桂荣. 知识约简的一种启发式算法[J]. 计算机研究与发展 , 1999, 36 (6) : 681-684 MIAO Duoqian, HU Guirong. A heuristic algorithm for reduction of knowledge[J]. Journal of computer research and development , 1999, 36 (6) : 681-684 |
| [4] | 王国胤, 于洪, 杨大春. 基于条件信息熵的决策表约简[J]. 计算机学报 , 2002, 25 (7) : 759-766 WANG Guoyin, YU Hong, YANG Dachun. Decision table reduction based on conditional information entropy[J]. Chinese journal of computers , 2002, 25 (7) : 759-766 |
| [5] | HU Feng, WANG Guoyin, HUANG Hai, et al. Incremental attribute reduction based on elementary sets[M]//SLEZAK D, WANG Guoyin, SZCZUKA M, et al. Proceedings of the 10th International Conference on Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. Berlin Heidelberg:Springer, 2005:185-193. |
| [6] | 杨明. 一种基于改进差别矩阵的属性约简增量式更新算法[J]. 计算机学报 , 2007, 30 (5) : 815-822 YANG Ming. An incremental updating algorithm for attribute reduction based on improved discernibility matrix[J]. Chinese journal of computers , 2007, 30 (5) : 815-822 |
| [7] | 冯少荣, 张东站. 一种高效的增量式属性约简算法[J]. 控制与决策 , 2011, 26 (4) : 495-500 FENG Shaorong, ZHANG Dongzhan. Effective incremental algorithm for attribute reduction[J]. Control and decision , 2011, 26 (4) : 495-500 |
| [8] | 尹林子, 阳春华, 王晓丽, 等. 基于标记可辨识矩阵的增量式属性约简算法[J]. 自动化学报 , 2014, 40 (3) : 397-404 YIN Linzi, YANG Chunhua, WANG Xiaoli, et al. An incremental algorithm for attribute reduction based on labeled discernibility matrix[J]. Acta automatica sinica , 2014, 40 (3) : 397-404 |
| [9] | SHU Wenhao, SHEN Hong. Updating attribute reduction in incomplete decision systems with the variation of attribute set[J]. International journal of approximate reasoning , 2014, 55 (3) : 867-884 DOI:10.1016/j.ijar.2013.09.015 |
| [10] | CHEN Hongmei, LI Tianrui, LUO Chuan, et al. A Decision-theoretic rough set approach for dynamic data mining[J]. IEEE transactions on fuzzy systems , 2015, 23 (6) : 1958-1970 DOI:10.1109/TFUZZ.2014.2387877 |
| [11] | LIANG Jiye, WANG Feng, DANG Chuangyin, et al. A group incremental approach to feature selection applying rough set technique[J]. IEEE transactions on knowledge and data engineering , 2014, 26 (2) : 294-308 DOI:10.1109/TKDE.2012.146 |
| [12] | QIAN Jin, YE Feiyue, LV Ping. An incremental attribute reduction algorithm in decision table[C]//Proceedings of the 7th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD). Yantai, China:IEEE, 2010, 4:1848-1852. |
| [13] | QIAN Jin, MIAO Duoqian, ZHANG Zehua, et al. Hybrid approaches to attribute reduction based on indiscernibility and discernibility relations[J]. International journal of approximate reasoning , 2011, 52 (2) : 212-230 DOI:10.1016/j.ijar.2010.07.011 |
| [14] | QIAN Jin, MIAO Duoqian, ZHANG Zehua, et al. Parallel attribute reduction algorithms using MapReduce[J]. Information sciences , 2014, 279 : 671-690 DOI:10.1016/j.ins.2014.04.019 |
| [15] | 康向平, 苗夺谦. 一种基于概念格的集值信息系统中的知识获取方法[J]. 智能系统学报 , 2016, 11 (3) : 287-293 KANG Xiangping, MIAO Duoqian. A knowledge acquisition method based on concept latticein set-valued information systems[J]. CAAI transactions on intelligent systems , 2016, 11 (3) : 287-293 |



