网络信息传播是人类借助网络传递或交流信息的社会性行为,目的是使信息得以广泛散发、吸收和利用。网络信息传播作为一种信息传播活动有其发展、变化的动态规律,并且与网络信息传播群体的行为紧密相关。网络信息传播群体是通过网络信息将网络中具有交互关系的个体联系在一起形成一种新型的网络虚拟群体,具有相同行为的个体构建出同一类型的单群体。根据信息传播行为的不同,可将网络信息传播群体分为信息发送单群体和信息接收单群体。
网络信息传播具有以下两个重要特性:
1) 网络信息传播具有流动性。网络信息的传播者将所拥有的信息发送给信息接收者,本轮信息传播过程完成后,信息传播并没有终止,而是信息的接收者瞬间又成为信息的拥有者,开始下一轮信息传播过程,网络信息传播在这种循环往复的过程中进行;
2) 网络信息传播具有主体性。信息传播个体具有主动的行为,传播个体的行为选择机制影响着信息传播过程。在网络信息传播过程中,传播主体追求传播效用,即网络中拥有信息的个体为了实现某种自身的利益诉求,采取能够获取更多收益的信息发送策略,例如发送真实信息或对信息进行加工处理形成失真信息进行发送。对于信息的接收者又会对接收到的信息进行策略选择,例如对接收到的信息进行直接转发或者加工后转发。网络信息传播过程中的策略选择,使传播主体之间形成了互动关系,产生了信息传播者之间的行为博弈,并促成了信息传播群体的行为演化。
在网络信息传播的研究中,为了能够更真实地反映行为主体的多样性和复杂性,并且可以为宏观调控群体行为提供理论依据,需要对网络信息传播群体的动态行为进行抽象和分析。演化博弈论[1]以具有有限理性的参与人群体为研究对象,把博弈理论分析和动态演化过程分析结合起来。在方法论上,它不同于经典博弈论将重点放在静态的均衡,而强调的是一种动态的均衡,关注群体行为的动态演化过程。
本文构造了符合网络信息传播特性的演化博弈模型,克服了使用其他模型存在的非主体性问题。由于网络信息传播具有流动性的特点,在研究过程中将信息接收单群体同样作为信息发送单群体来看待,仅形成同一类的信息传播者单群体。网络信息传播群体中的个体发送真实信息和发送失真信息获得不同收益的行为关系在本文中使用构建的演化博弈模型来描述和分析,个体在寻求自身利益的交互过程中相互制约,最终形成群体行为的平衡点。
在研究演化稳定策略ESS(evolutionary stable strategies)的同时,也需要对群体行为的动态演化过程进行刻画,从动力学角度分析稳定均衡。在网络信息传播群体中,信息的传播和信息传播群体行为的选择都遵从某种规律的动力学。本文采用属于收益正性动态的复制者动态[2]模型来刻画网络群体行为的动力学机制,即所有超出平均收益的纯策略都具有正的增长率,而所有低于平均收益的纯策略都具有负的增长率。
本文的主要贡献在于将演化博弈论应用到分析网络信息传播单群体行为的研究中。通过对网络信息传播单群体中随机个体的交互博弈分析,描述信息传播群体行为的动态演化过程以及动态均衡下的策略选择,并为下一步的信息传播多群体间的行为研究打下理论基础。为了建立形式化的演化博弈模型并为下一步的模拟实验打下基础,本文将网络环境中的真实信息传播个体用多Agent系统[3]中的Agent进行模拟,来帮助分析网络信息传播群体的行为决策。通过对用户的行为规律进行深入挖掘分析,从而为进一步网络信息预测和控制[4]的研究和应用打下基础。
1 研究机制及方法 1.1 演化博弈论演化博弈理论是一种适合解决网络中动态博弈问题的方法。在网络信息传播的应用背景下,使用演化博弈[5]相对经典博弈来对信息传播行为进行研究,具有以下优势:
1) 经典博弈要求参与者具有绝对理性,包括目标理性和过程理性。参与者以追求收益最大化为目的,并可以准确无误地选择最优反应策略。完全理性在现实中很难满足,尤其是当应用环境和决策问题较复杂时,参与者存在很大的理性局限,从而对参与者的决策和行为选择方式会产生很大影响。因此,在网络信息传播的应用背景下,采用有限理性的演化博弈进行分析更加适用。
2) 经典博弈是一种静态博弈,能够使个体在瞬间获取最优结果从而达到静态均衡。在网络信息传播的大平台下,由于信息具有流动性,信息在网络中的广泛传播需要一定的时间阶段,且不可忽略,同时个体的信息传播行为随时间和交互次数进行动态调整从而达到动态均衡。因此,在网络信息传播的应用背景下,采用能够体现动态特性的演化博弈进行分析更加适用。
3) 经典博弈主要关注参与者的个体行为。在网络大环境中,个体行为并不能对整个网络产生足够的影响,能对网络信息传播产生严重影响的是群体行为,并且群体行为的变化是一个长期动态调整的过程。因此,在网络信息传播的应用背景下,采用研究群体行为的演化博弈进行分析更加适用。
4) 在网络信息传播的应用背景下,信息传播个体之间随机地发生交互,个体间进行的是多次博弈,且两次遇到相同个体的概率很小,因此采用演化博弈对传播行为进行研究可以避免经典博弈理论中个体记忆的概念,具有更简洁的理论框架,因此更适合应用到网络信息传播群体行为的研究中。
1.2 复制者动态学习模型演化博弈论的有限理性体现在参与者的学习能力上,参与者的行为选择可以依据前人的经验、学习与模仿他人行为,在博弈过程中通过动态学习寻找较好的策略。选择动态模拟演化博弈中参与者的学习和决策过程,来刻画有限理性下的决策机制和群体行为的动态演化。演化博弈基本的选择动态如式(1)所示。
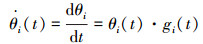 |
(1) |
式中:θi(t)表示在t时刻选择策略i的个体在群体中所占的比例;函数gi(t)表示具体的选择过程,不同的学习选择机制对应不同的函数。
复制者动态是针对学习速度较慢的成员组成的大群体进行随机配对反复博弈时采用的选择动态,能用来描述单群体策略的动态调整过程[6],如式2所示,θi的增长率是选择策略si的效用ut(si)与群体平均效用ut差的严格增函数,体现在成功的策略由于其高收益而在群体中不断采纳[7]。同时复制者动态能够描述没有明显结构的无限人口中的各种策略的占有率随着时间的变化[8]。
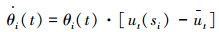 |
(2) |
由于在网络信息传播过程中,网络上的每个点都可以成为信息传播的参与者且数量巨大,因此本文对网络信息传播群体进行演化博弈分析时采用复制者动态学习模型是适用的。
1.3 有限理性Agent为了利于形式化建模和分析,以及为下一步的模拟实验奠定基础,可以用具有有限理性[9]和学习能力的Agent来模拟演化博弈模型中的参与者。在演化博弈研究中,参与者只需要具有有限理性和学习能力,智能体Agent正好符合这一特性。Agent的理性在于多Agent交互时,能够在多个可能策略选择间做出合理的选择。在多Agent系统中,Agent不是孤立存在的,但Agent的资源和能力却是有限的,Agent的行为必须满足某种理性[10],但很难满足逻辑理性和效用理性[11]。同时,Agent具有学习能力,因此Agent是有限理性而不是完全理性的。
本文在网络信息传播背景下,使用Agent来模拟有限理性的真实信息传播者是合理的。
2 建立模型 2.1 前提条件本文基于Agent的网络信息传播群体行为的演化博弈分析的前提如下。
1) 进行的是网络信息传播单群体的行为演化分析,这种分析思路符合网络信息流动性的特点。
2) 是从全局进行考察,网络上的每个人都可以作为信息的传播者。在进行信息传播时,信息传播者的策略分为对所拥有信息进行真实发送,或者对信息进行加工处理成失真信息后发送。
3) 在演化博弈分析时,不考虑决策环境中的不确定性对策略选择的影响,因此群体行为的动态演化过程是一种无突变的选择学习[12]。
4) 用Agent群体模拟信息发送群体,群体中的每一个信息传播个体用一个Agent个体表示。
5) 以网络信息传播为研究背景,网络中信息传播者群体庞大,因此用来进行行为模拟的Agent群体中的个体都属于同一类单群体,且数量足够大并混合均匀,即群体中任意两个个体等可能地进行随机博弈。
2.2 演化博弈模型的形式化定义网络信息传播中,Agent个体的适应性是指它和群体中一个随机相遇的Agent互动得到的预期收益。群体中任意两个Agent相遇进行博弈的收益矩阵,如图 1所示,s1表示发送真实信息,s2表示发送失真信息。由于进行的是单群体博弈分析,因此建立的收益矩阵是对称的。

|
| 图 1 群体中两个Agent交互时的收益矩阵(B>A>C) Fig. 1 Pay-off matrix of two interactive Agents (B>A>C) |
网络背景下,之所以存在发送失真信息的策略,是因为网络信息传播者具有主体性且信息本身具有不确定性,因此存在发送失真信息会带来更多收益的可能性。在图 1矩阵中,B > A对应现实中的情景是通过发送某些虚假信息或通过造谣来达到信息真假难辨的目的从而获利,博弈双方策略不同时,发送失真信息获得的收益大于发送真实信息获得的收益。C < A对应现实中的情景是如果博弈双方都发送虚假信息会导致社会不信任的出现,从而小于双方都发送真实信息的收益。为了方便计算,将C取值为B/2。
定义1 六元组〈N, S, U, P, E, S*〉为网络信息传播中,用多Agent模拟的信息传播群体的演化博弈模型,其中
1) N={Agent1, Agent2, ..., Agentn}为Agent同类群体,Agent群体中的任何一个Agenti都可以发送信息。
2) 因为N是同一群体,因此N中的每一个Agenti都有相同的策略备选项集S={s1, s2},其中s1和s2都表示纯策略。该模型中,s1表示发送真实信息,s2表示发送失真信息。
3) U={U1, U2,…, Un},Ui是Agenti的收益函数,Ui(sj1, sj2)表示在纯策略组合(sj1, sj2)之下Agenti的收益值,sj1∈S,sj2∈S。表 1为Agent1、Agent2交互双方策略组合的收益函数列表。
| Agent1的收益函数 | Agent2的收益函数 |
| U1(s1, s1)=A | U2(s1, s1)=A |
| U1(s1, s2)=A | U2(s1, s2)=B |
| U1(s2, s1)=B | U2(s2, s1)=A |
| U1(s2, s2)=B/2 | U2(s2, s2)=B/2 |
4) P是混合策略集,是将策略备选项集的空间从有限纯策略集S扩展到S的概率分布空间。
P={p1, p2, …, pn}
式中:Pi是Agenti的混合策略概率, 即Agenti采用以Pi发送真实信息,以1-pi发送失真信息的混合策略,且0 < pi < 1。
5) E(si)是Agenti采取策略si的期望收益函数,si∈S,i=1, 2。
6) S*为建立的演化博弈模型的演化稳定策略(ESS)的集合。若存在s*∈P,对于所有的s∈P且s≠s*,满足E(s*)>E(s),则s*为演化博弈模型的ESS,即s*∈S*,s*可以是演化稳定纯策略,也可以是演化稳定混合策略。
3 群体行为的演化博弈分析 3.1 群体中个体行为的经典博弈分析因为网络信息传播个体行为对网络信息传播群体行为的涌现趋势和演化结果有重要的影响,即网络群体行为的形成是离不开群体内的个体行为。因此,对于个体信息传播行为进行建模、分析和预测也是网络信息群体行为研究中的重要内容。
结合图 1中的收益矩阵进行完全信息静态博弈分析,博弈双方的策略组合(s1, s2)和(s2, s1)为纯策略纳什均衡,并且是非严格对称纳什均衡。
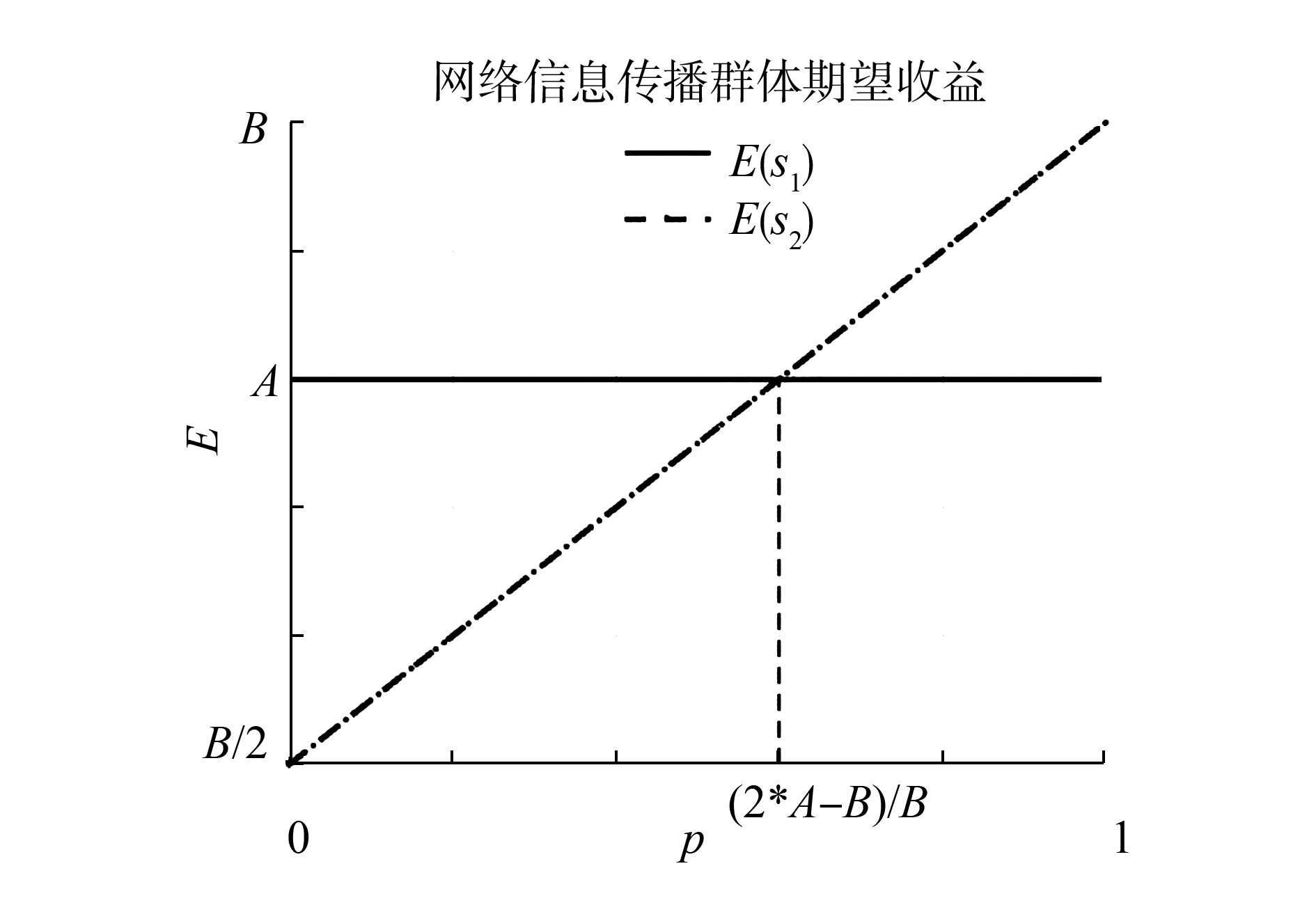
将随机因素引入到参与者Agent的行为选择中,Agent以p(0 < p < 1)概率发送真实信息,以1-p概率发送失真信息。Agent发送真实信息和发送失真信息的期望收益如式(3)所示,收益曲线如图 2。
|
| 图 2 个体Agent的收益曲线图 Fig. 2 Pay-off diagram of individual Agent |
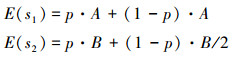 |
(3) |
对于Agent群体中的个体来说,在静态博弈下通过式(4)的求解过程,获知Agent以概率p=(2A-B)/B发送真实信息,以概率1-(2A-B)/B发送失真信息是混合策略纳什均衡,并且是对称混合纳什均衡。
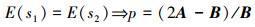 |
(4) |
定义2 演化稳定策略[9]。策略T以x占比入侵策略S,表示总体中有x占比的群体采用策略T,1-x占比的群体采用策略S,其中x是一个小于1的正数。假设存在一个正数y,当任何其他策略T以任何x < y的程度入侵策略S时,采用策略S的个体适应性严格高于采用策略T的个体适应性,则称策略S是演化稳定的。策略T和S是纯策略时,策略S是演化稳定纯策略。如果T和S中存在随机因素,是两种不同概率的策略组合时,策略S是演化稳定混合策略。
演化稳定策略是演化博弈的静态均衡,根据建立的网络信息传播群体的演化博弈模型,结合定义2进行模型演化稳定策略的分析,具体过程如下。
1) 分析发送真实信息的策略是否是ESS,即判断以x占比发送失真信息的群体入侵以1-x占比发送真实信息的群体时,期望收益E(s1)是否大于期望收益E(s2)、E(s1)和E(s2)如式5所示。
 |
(5) |
如果E(s1)>E(s2),则需要满足条件x>2(B-A)/B,如果不满足该条件,即x < 2(B-A)/B,则E(s1) < E(s2),因此群体发送真实信息的策略不是ESS。
2) 分析发送失真信息的策略是否是ESS,即判断以x占比发送真实信息的群体来入侵以1-x占比发送失真信息的群体时,期望收益E(s2)是否大于期望收益E(s1),E(s2)和E(s1)如式6所示。
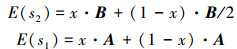 |
(6) |
如果E(s2)>E(s1),则需要满足条件x>(2A-B)/B,如果不满足该条件,即x < (2A-B)/B,则E(s2) < E(s1),因此群体发送失真信息的策略不是ESS。
3) 分析混合策略是否是ESS
1-x占比的群体以p概率发送真实信息,以1-p概率发送失真信息。x占比的群体以q概率(q≠p)发送真实信息,以1-q概率发送失真信息来入侵。如果采取混合策略p的期望收益大于采取混合策略q的期望收益,即E(p)>E(q)时,则p是演化稳定混合策略。
用F(p, q)表示采取策略p的个体Agent与采取策略q的个体Agent交互时,采取p策略的个体Agent的期望收益。采取p和q策略的期望收益计算过程如式7所示。
 |
(7) |
性质1 对所有的q≠p来说,如果E(p)>E(q),则p策略是演化稳定策略,需要满足以下两个条件之一[9]:
1) F(p, p)>F(q, p),则采取p策略是强演化稳定策略;
2) F(p, p)=F(q, p)且F(p, q)>F(q, q),则采取p策略是弱演化稳定策略。
从3.1节可知,静态博弈模型存在对称混合纳什均衡,因此结合性质1来验证以概率p=(2A-B)/B发送真实信息以概率1-p发送失真信息的混合策略是否是弱演化稳定策略,验证过程如下:
验证1 建立的演化博弈模型不存在强演化稳定策略。
从3.1小节可获知,以概率p=(2A-B)/B发送真实信息,以概率1-p发送失真信息是混合策略纳什均衡,并且是对称混合纳什均衡。因为在p < (2A-B)/B或p > (2A-B)/B时,会得到F(p, p)和F(q, p)相反的比较结果。此结果也验证了如果演化稳定策略不是纯策略,那混合策略只可能是弱演化稳定策略。
验证2 混合纳什均衡策略是否是演化博弈模型的弱演化稳定策略。
当p=(2A-B)/B时,q无论为何值时,都存在式8和式9结果。
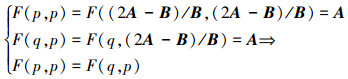 |
(8) |
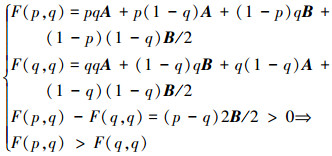 |
(9) |
因此p=(2A-B)/B是弱演化稳定策略。
对于给出的演化博弈模型来说,不存在演化稳定纯策略,但存在演化稳定混合策略,即群体中的个体对于已经拥有的信息,采用p=(2A-B)/B概率发送真实信息以1-p概率发送失真信息的混合策略,会在整个网络信息传播的大环境中生存并稳定下去。通过演化稳定策略可以来预测在网络信息传播中,最终群体传播者的行为策略。
3.3 复制者动态分析演化稳定策略属于静态的均衡概念,但无法刻画群体行为的动态演化过程,动态的稳定均衡与具体的演化过程有关,以下通过复制者动态来描述群体行为的选择过程,从而分析均衡的动态稳定性。
在网络信息传播群体中,群体中采取发送真实信息策略的比例为x,发送失真信息策略的比例为1-x。发送真实信息群体的收益为U1,发送失真信息群体的收益为U2,U表示发送信息群体的平均收益,如式(10)所示。不同行为群体的收益随比例x的变化曲线如图 3所示。群体选择的复制动态方程如式(11)所示。

|
| 图 3 Agent群体收益曲线图 Fig. 3 Pay-off diagram of Agent population |
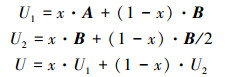 |
(10) |
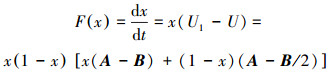 |
(11) |
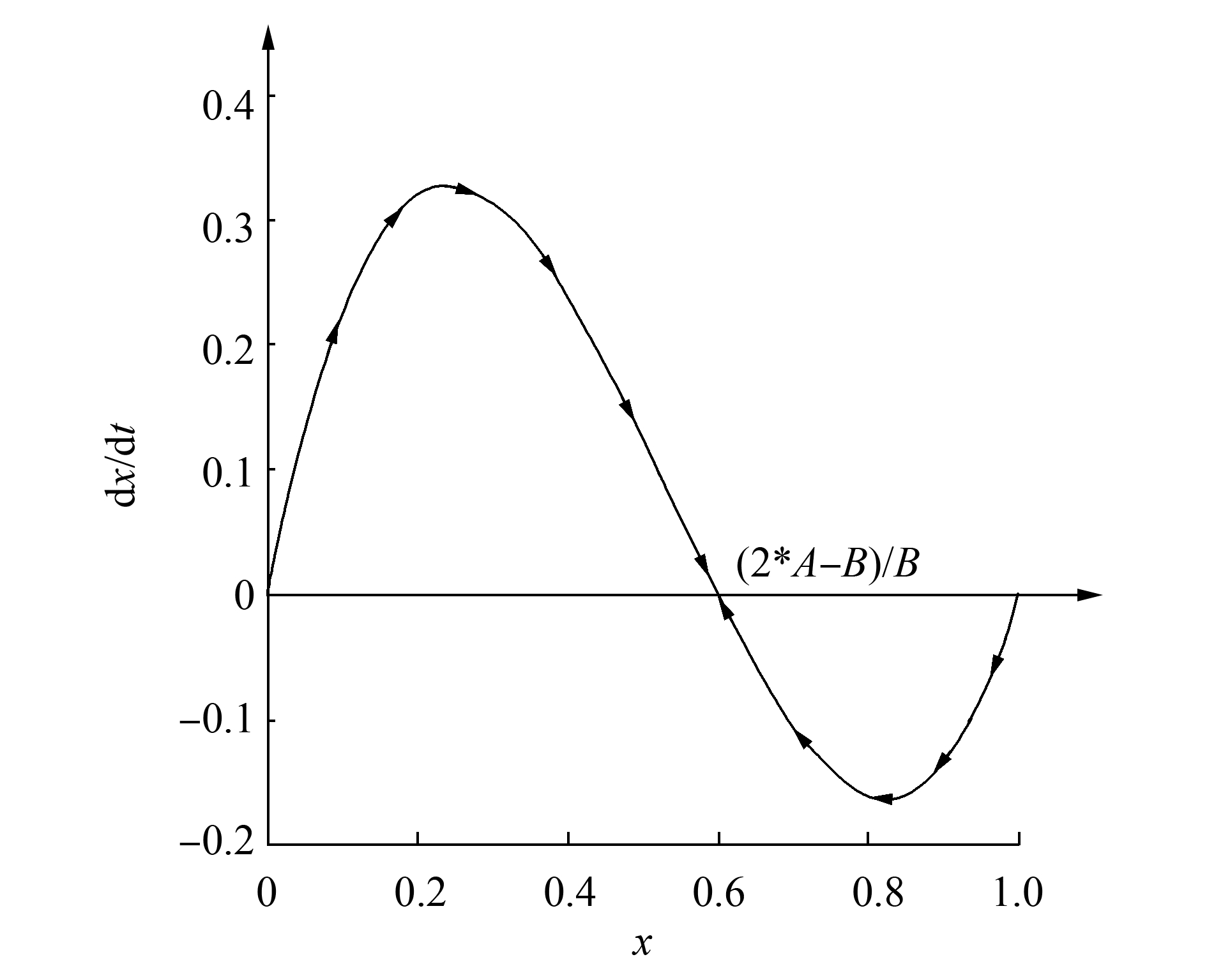
当F(x)=0时,复制动态稳定状态为:x*=0,x*=1,x*=(2A-B)/B。复制动态相位图如图 4所示,描述随着时间的推移网络信息传播群体行为的演化过程。根据微分方程的稳定性定理,一个稳定状态必须对微小扰动具有稳健性才能称为进化稳定策略。对于稳定状态x*,当F′(x*) < 0时,x*才为演化稳定策略ESS。对于3个动态稳定点,只有x*=(2A-B)/B对应F′(x*) < 0,因此x*=(2A-B)/B是演化博弈模型的演化稳定策略。
|
| 图 4 Agent群体复制者动态相位图 Fig. 4 Replicator dynamics phase diagram of Agent population |
定义3 静止点。如果群体结构一旦处于点s*,且群体结构一直稳定在这个点,那么群体结构s*就是一个静止点[9]。
x*=0,x*=1,x*=(2A-B)/B都是网络信息传播群体的静止点。但复制者动态要想达到静止点,必须要求该静止点具有局部稳定性,具有局部稳定的静止点称为吸引子。
定义4 吸引子[9]。如果当群体结构一开始接近点s*,且最终群体结构会走向s*,那么这个静止点s*就是一个吸引子,即群体结构收敛到吸引子。
从网络信息传播群体复制者动态相位图上可以看出,全部采取传播失真信息的Agent群体结构(x*=0),和全部采取传播真实信息的Agent群体结构(x*=1)是两个静止点但不是吸引子。采取发送真实信息Agent的比例x*=(2A-B)/B是一个吸引子。除了x*=0和x*=1两个静止点,其他区域都是吸引子x*=(2A-B)/B的吸引域。在吸引域内,采取发送真实信息策略的群体比例x最终会稳定在动态均衡点x*=(2A-B)/B上,使整个群体结构处于稳定状态。
3.4 演化稳定策略与复制者动态之间的关系复制者动态产生的动态均衡与演化稳定策略有很强的关联性。通过演化稳定策略可以刻画稳定群体的行为,描述演化博弈的静态均衡。演化稳定策略可以是纯策略也可以混合策略,强调群体中个体行为的选择。通过复制者动态可以刻画群体行为的选择过程,可以分析演化博弈的动态均衡(吸引子),即处于稳定状态下的群体结构。复制者动态强调群体行为的选择,选择仅限于纯策略。针对同一个演化博弈模型分析得到的演化稳定策略中的概率值,与通过复制者动态分析得到的稳定群体结构中吸引子上对应的比例数值是相等的。
在已构建的演化博弈模型中,存在一个弱演化稳定策略,即群体中的所有个体都以p=(2A-B)/B概率发送真实信息,以1-p概率发送失真信息,使整个群体行为处于稳定状态。针对演化博弈模型构建的复制者动态,x=(2A-B)/B比例的群体发送真实消息,1-x比例的群体发送失真消息,将使整个群体结构处于稳定状态。
4 相关工作与比较网络信息传播的研究可以从网络信息传播个体行为、单群体行为和群体间行为三方面进行[12]。网络信息传播个体的行为对网络信息传播群体行为的涌现和演化结果有重要影响,对个体行为进行分析和预测是网络群体行为研究中的重要内容。作者在文献[13]中,使用经典博弈论对网络信息传播个体的行为进行了建模和分析。本文使用演化博弈论对网络信息传播单群体的行为进行建模和分析。而网络信息传播多群体间的行为研究将作为下一步的工作内容。
文献[14]关注危机信息在网络上传播的动力学研究。文献[15]关注具有竞争性的信息在网络上传播的演化分析。文献[14-15]都强调被传播的网络信息具有某一特殊性,而本文中被传播的网络信息更具有一般性。文献[16-17]中建立的观点交互模型主要描述网络信息传播者间交互规则在用户观点上的演化过程,而本文主要描述网络信息传播群体在行为选择上的演化过程。文献[18]是对网络群体事件的演化博弈分析,主要关注政府和网民行为的演化过程。文献[19]是对网络谣言传播行为的分析,主要关注谣言发送者与政府或谣言发送者与网民的行为博弈。文献[20]关注不同网络拓扑结构对网络群体行为产生不同演化趋势的影响。文献[15-20]和本文的研究虽然都是使用演化博弈模型来进行建模分析,但应用的背景问题不同。文献[21]模拟信息传播过程的各个不同阶段,将信息传播个体的知识结构等因素引入到博弈模型中,从而研究信息传播个体自身的特性因素对个体传播行为的影响。而本文研究信息传播群体的行为而非个体的行为,并且在演化模型中并未考虑群体的知识结构等因素对适应性的影响。将群体的特性因素引入模型进行分析研究可以作为下一步研究的内容。
文献[22]使用基于传染病传播机制的信息传播模型来建模网络信息传播过程。许多研究者认为复杂网络上的信息传播与传染病在人群中的扩散具有相似性。经典的网络信息传播模型是SIR(Susceptible-Infected-Recovered)模型及其改进模型[23]。虽然SIR模型能很好地体现网络信息传播具有流动性的特性,但不能体现网络信息传播具有主体性的特性。因为在SIR模型中,将用户行为默认为自动转发行为,即将接收到的信息直接转发,而现实中的信息转发常伴随对信息进行加工处理而非直接转发,该过程受传播者主体性的影响,传播者会根据自身的期望收益来进行策略选择,而在SIR模型中却无法体现传播者的利益诉求。另外,对SIR模型的研究常结合具体的网络类型[24],例如随机网络、小世界网络、无标度网络等,而缺乏在一般网络上的分析研究。
演化博弈模型作为研究网络信息传播行为的强有力工具,与SIR及其扩展模型、Markov随机模型、随机Petri网模型相比,其优越性表现在通过它能很好地刻画个体和群体在与其他个体或群体交互过程中,行为随时间、环境、经验和学习等因素的动态演化。本文建立的演化博弈模型不仅考虑了信息传播流动性的特点,而且将信息发送者和信息接收者统归于信息传播者大类上,并把信息传播者的偏好和利益诉求考虑其中,克服了SIR模型不能体现传播主体性的问题,更加符合网络信息传播的现实情形。
本文采用Agent来模拟有限理性的信息传播者和为建立的演化博弈模型进行形式化定义也是本文的创新之处。结合多Agent技术进行网络信息传播群体行为的研究不仅可以提供一种理论分析的工具和视角,关注群体传播行为的抽象,而且可以为基于实证数据[25]的仿真实验奠定基础。
5 结论本文以网络信息传播为背景,将演化博弈论作为主要分析工具,同时结合多Agent技术对网络信息传播者群体行为进行模拟,采用复制者动态对群体行为到达均衡解的动态演化过程进行建模。通过计算群体行为达到稳定状态时的吸引子,可以分析和探讨演化稳定策略与复制者动态的吸引子之间的关系,并可以验证在网络信息传播的背景下,针对信息传播群体的行为,复制者动态产生的结果与演化稳定策略有很强的关联性,同时可以揭示网络信息传播群体的行为规律。在下一阶段的研究中,可以从以下几个研究内容和方法出发:
1) 采取基于智能优化算法的学习、神经网络的学习、最优反映学习、信念学习[26]等决策机制来分析演化过程;
2) 考虑到群体行为具有随机性的特点,将随机性动态演化与演化博弈过程相结合,建立随机演化博弈模型[27],从而解决确定性演化博弈模型存在的问题;
3) 考虑到网络的拓扑结构会影响群体行为的演化趋势[28],针对不同类型的复杂网络开展信息传播群体行为的演化博弈分析[29]。
| [1] | SELTEN R. Evolutionary stability in extensive two-person games[J]. Mathematical social sciences , 1983, 5 (3) : 269-363 DOI:10.1016/0165-4896(83)90012-4 |
| [2] | CRESSMAN R. Dynamic stability in symmetric extensive form games[J]. International journal of game theory , 1997, 26 (4) : 525-547 DOI:10.1007/BF01813889 |
| [3] | DIAZ B A. Agent based models on social interaction and demographic behaviour[D]. Wien:Vienna University of Technology, 2010:1-93. |
| [4] | EASLEY D, KLEINBERG J. Networks, crowds, and markets:reasoning about a highly connected world[M]. Cambridge: Cambridge University Press, 2010 : 1 -744. |
| [5] | SCATA M, DI STEFANO A, LA CORTE A, et al. Combining evolutionary game theory and network theory to analyze human cooperation patterns[J]. Chaos, solitons & fractals , 2016, 91 : 17-24 |
| [6] | 王先甲, 全吉, 刘伟兵. 有限理性下的演化博弈与合作机制研究[J]. 系统工程理论与实践 , 2011, 31 (S1) : 82-93 WANG Xianjia, QUAN Ji, LIU Weibing. Study on evolutionary games and cooperation mechanism within the framework of bounded rationality[J]. Systems engineering-theory & practice , 2011, 31 (S1) : 82-93 |
| [7] | BLOEMBERGEN D, CALISKANELLI I, TUYLS K. Learning in networked interactions:a replicator dynamics approach[M]//HEADLEAND C J, TEAHAN W J, CENYDD L A. Artificial Life and Intelligent Agents. Switzerland:Springer, 2015:44-58. |
| [8] | HOFBAUER J, SIGMUND K. Evolutionary game dynamics[J]. Bulletin of the American mathematical society , 2003, 40 (4) : 479-519 DOI:10.1090/S0273-0979-03-00988-1 |
| [9] | HARRINGTON JR J E. Game, strategies, and decision making[M]. New York: Worth Publishers, 2008 : 1 -540. |
| [10] | 蒋建国, 张国富, 夏娜, 等. 一种基于理性Agent的任务求解联盟形成策略[J]. 自动化学报 , 2008, 34 (4) : 478-481 JIANG Jianguo, ZHANG Guofu, XIA Na, et al. A task oriented coalition formation strategy based on rational agents[J]. Acta automatica sinica , 2008, 34 (4) : 478-481 |
| [11] | 程显毅, 石纯一. Agent社会理性的研究[J]. 软件学报 , 2001, 12 (12) : 1825-1829 CHENG Xianyi, SHI Chunyi. Research on the socially rationality of agent[J]. Journal of software , 2001, 12 (12) : 1825-1829 |
| [12] | 王元卓, 于建业, 邱雯, 等. 网络群体行为的演化博弈模型与分析方法[J]. 计算机学报 , 2015, 38 (2) : 282-300 WANG Yuanzhuo, YU Jianye, QIU Wen, et al. Evolutionary game model and analysis methods for network group behavior[J]. Chinese journal of computers , 2015, 38 (2) : 282-300 |
| [13] | 郭艳燕, 童向荣, 刘其成, 等. 基于博弈论的网络信息传播模型的研究[J]. 计算机科学 , 2014, 41 (3) : 238-244 GUO Yanyan, TONG Xiangrong, LIU Qicheng, et al. The models of network information propagation based on the game theory[J]. Computer science , 2014, 41 (3) : 238-244 |
| [14] | 张乐.危机信息传播的社会网络结构和传播动力学研究[D].合肥:中国科学技术大学, 2009:1-90. ZHANG Le. Research on social network structure and dynamics of crisis information dissemination[D]. Hefei:University of Science and Technology of China, 2009:1-90. |
| [15] | YU Jianye, WANG Yuanzhuo, LI Jingyuan, et al. Analysis of competitive information dissemination in social network based on evolutionary game model[C]//Proceedings of the 2012 Second International Conference on Cloud and Green Computing. Xiangtan, China:IEEE, 2012:748-753. |
| [16] | SOBKOWICZ P. Modelling opinion formation with physics tools:call for closer link with reality[J]. Journal of artificial societies and social simulation , 2009, 12 (1) : 11 |
| [17] | CASTELLANO C, FORTUNATO S, LORETO V. Statistical physics of social dynamics[J]. Reviews of modern physics , 2009, 81 (2) : 591-646 DOI:10.1103/RevModPhys.81.591 |
| [18] | 肖人彬, 张耀峰. 网络群体事件信息传播的演化博弈分析[J]. 复杂系统与复杂性科学 , 2012, 9 (1) : 1-7 XIAO Renbin, ZHANG Yaofeng. Evolutionary game analysis of information spread in network mass events[J]. Complex systems and complexity science , 2012, 9 (1) : 1-7 |
| [19] | 张芳, 司光亚, 罗批. 谣言传播模型研究综述[J]. 复杂系统与复杂性科学 , 2009, 6 (4) : 1-11 ZHANG Fang, SI Guangya, LUO Pi. A survey for rumor propagation models[J]. Complex systems and complexity science , 2009, 6 (4) : 1-11 |
| [20] | SKYRMS B, PEMANTLE R. A dynamic model of social network formation[M]//GROSS T, SAYAMA H. Adaptive Networks. Berlin Heidelberg:Springer, 2009:231-251. |
| [21] | QIU Wen, WANG Yuanzhuo, YU Jianye. A game theoretical model of information dissemination in social network[C]//Proceedings of 2012 International Conference on Complex Systems. Agadir, Morocco:IEEE, 2012:1-6. |
| [22] | ANDERSON R M, MAY R M, ANDERSON B. Infectious diseases of humans:dynamics and control[M]. Oxford: Oxford University Press, 1992 : 1 -766. |
| [23] | ANTULOV-FANTULIN N, LANCIC A, STEFANCIC H, et al. FastSIR algorithm:a fast algorithm for the simulation of the epidemic spread in large networks by using the susceptible-infected-recovered compartment model[J]. Information sciences , 2013, 239 : 226-240 DOI:10.1016/j.ins.2013.03.036 |
| [24] | LLOYD A L, MAY R M. How viruses spread among computers and people[J]. Science , 2001, 292 (5520) : 1316-1317 DOI:10.1126/science.1061076 |
| [25] | KIESLING E, GüNTHER M, STUMMER C, et al. Agent-based simulation of innovation diffusion:a review[J]. Central European journal of operations research , 2012, 20 (2) : 183-230 DOI:10.1007/s10100-011-0210-y |
| [26] | 王先甲, 刘伟兵. 有限理性下的进化博弈与合作机制[J]. 上海理工大学学报 , 2011, 33 (6) : 679-686 WANG Xianjia, LIU Weibing. Evolutionary game and cooperation mechanisms based on bounded rationality[J]. Journal of university of Shanghai for science and technology , 2011, 33 (6) : 679-686 |
| [27] | GAO Xing, ZHONG Weijun, MEI Shue. Stochastic evolutionary game dynamics and their selection mechanisms[J]. Computational economics , 2013, 41 (2) : 233-247 DOI:10.1007/s10614-012-9320-4 |
| [28] | SKYRMS B, PEMANTLE R. A dynamic model of social network formation[M]//GROSS T, SAYAMA H. Adaptive Networks. Berlin Heidelberg:Springer, 2009:231-251. |
| [29] | 王龙, 伏锋, 陈小杰, 等. 复杂网络上的演化博弈[J]. 智能系统学报 , 2007, 2 (2) : 1-10 WANG Long, FU Feng, CHEN Xiaojie, et al. Evolutionary games on complex networks[J]. CAAI transactions on intelligent systems , 2007, 2 (2) : 1-10 |



