2. 河北省计算数学与应用重点实验室, 河北 石家庄 050024
2. Hebei Key Laboratory of Computational Mathematics and Applications, Shijiazhuang 050024, China
粗糙集理论由Pawlak[1]于1982年提出, 是一种有效处理模糊和不确定性知识的数学工具,其在机器学习、模式识别、决策分析和数据挖掘等领域得到广泛应用[2-5]。经典粗糙集理论基于等价关系定义集合的上、下近似, 然而随着现实世界中的数据在结构和形式上日益复杂化和多样化,经典粗糙集有时不再能满足实际问题的处理需求。为此众多学者从不同角度对经典粗糙集模型进行了扩展[5-8],提出了覆盖粗糙集、多粒度粗糙集、变精度粗糙集、概率粗糙集、模糊粗糙集等。其中,覆盖粗糙集是将经典粗糙集中的划分推广成更一般的覆盖,增强了其处理数据的能力[7, 9]。
从粒计算的角度来看,Pawlak粗糙集及推广形式都是基于单一二元关系,均可被称做单粒度粗糙集。然而,在许多实际应用中,需要由多个二元关系诱导出的多粒度结构对目标概念进行刻画。为此,钱宇华等[8, 10]提出了基于全域中多个等价关系的经典多粒度粗糙集模型。苗夺谦等[11]在覆盖近似空间中提出4种乐观多粒度覆盖粗糙集模型,其中集合的第一、二型近似分别基于论域中对象极小描述的交和并,集合的第三、四型近似分别基于论域中对象极大描述的交和并。
另一方面,Dempster-Shafer(DS)证据理论产生自20世纪60年代。Dempster[12]提出了集值映射的概念, 并定义了上、下概率。随后, Shafer[13]用信度函数对上、下概率重新进行诠释, 创立“证据的数学理论”。Dempster还定义了著名的Dempster证据组合规则, 该理论中的基本概念是信度函数, 包括信任函数和似然函数,并以此来度量知识的不确定性。与粗糙集理论相类似,证据理论也是一种处理不确定性的有力工具[14-16]。许多专家对粗糙集和证据理论之间的关系进行了研究和推广。姚一豫[17]指出可以用信任函数和似然函数对粗糙集中的上、下近似算子进行解读;吴伟志等[16]将信任结构与近似空间相结合,从证据理论的角度研究Pawlak粗糙集的知识约简;陈德刚等[18]在统一框架下对若干覆盖近似算子进行分类,基于粒和证据理论对这些覆盖粗糙近似算子进行度量,并且用信任函数和似然函数对邻域覆盖粗糙集中上、下近似算子进行了度量,进而建立了上述函数与邻域信息系统属性约简之间的关系[19]。
将证据理论与多粒度粗糙集模型相结合是目前的研究热点之一[20-21],谭安辉[22]基于证据理论刻画了不完备信息系统中多粒度粗糙集的数值属性,指出只有悲观多粒度粗糙集的数值属性可以由信任结构刻画,并构建了一种多粒度粗糙集的属性约简算法;林国平[14]结合证据理论和多粒度粗糙集,提出一种新的融合多源信息的方法。然而,上述研究都没有考虑过如何构建多粒度覆盖粗糙集的信任结构以及如何用证据理论刻画多粒度覆盖粗糙集的数值属性。基于上述启发,本文首先在苗夺谦等[11]提出的4种乐观多粒度覆盖粗糙集模型的基础上定义4种悲观多粒度覆盖粗糙集模型,然后基于证据理论给出多粒度覆盖粗糙集的信任结构。通过集合的交运算和关系划分函数建立多粒度覆盖与单粒度划分之间的关系,进而建立了多粒度覆盖粗糙集和证据理论之间联系。
1 相关概念 1.1 Pawlak粗糙集相关概念定义1 令S=(U, C∪D, Va, f)是信息系统[1],其中U={x1, x2, x3, …, xn}是非空有限对象集,称为论域;C是条件属性集,D是决策属性集,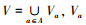
∀B⊆C决定一个二元不可辨识关系[1]RB,定义为
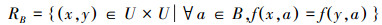 |
显然,RB是集合U上的等价关系,对于B⊆C,关系RB产生U的一个划分U/RB={[x]B|x∈U},即[x]B={y∈U|(x, y)∈RB}。
定义2 令S=(U, R)为近似空间,R是U上的等价关系,∀X⊆U, 称R(X)和R(X)为X关于R的上、下近似[1],如果
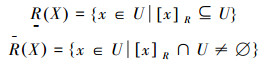 |
若R(X)≠R(X),称X为粗糙集[1],否则称X为可定义集[1]。
1.2 覆盖粗糙集相关概念定义3 令U为论域,C是U的一族子集。如果ø∉C且∪C=U,则称C是U的一个覆盖[23];称序对(U, C)是覆盖近似空间[23]。
定义4 令(U, C)为覆盖近似空间,其中C={C1, C2, …, Cp}。∀X⊆U, 称R(X)和R(X)为X关于C的上、下近似[23], 如果
 |
定义5 令(U, C)为覆盖近似空间,∀x∈U,集合mdC(x)和MDC(x)分别称x关于C的极小描述和极大描述[11],如果
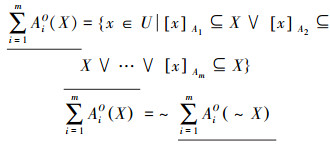 |
下面简要给出多粒度粗糙集的两种模型,即乐观多粒度粗糙集和悲观多粒度粗糙集。
定义6 令S=(U, A)是信息系统,A是属性集合,A1, A2, …, Am⊆A, 其中m是自然数。∀X⊆U, X关于A1, A2, …, Am的乐观多粒度上、下近似[8, 10]为
 |
式中~X=U-X。
定义7 令S=(U, A)是信息系统,A是属性集合,A1, A2, …, Am⊆A, 其中m是自然数。∀X⊆U, X关于A1, A2, …, Am的悲观多粒度上、下近似[8, 10]为
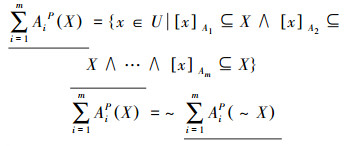 |
式中~X=U-X。
2.4 证据理论相关概念定义8 令U为论域,2U是U的全体子集,集函数m:2U→0, 1称为概率指派函数[22],即mass函数,如果
1) m(ø)=0;
2) ∑X⊆Um(X)=1。
若m(X)≠0, 则称X为m的焦元。
定义9 令U为论域,m:2U→[0, 1]是一个基本概率指派函数。集函数Bel:2U→[0, 1]称为U上的信任函数[19],如果Bel(X)=∑X′⊆Xm(X′), ∀X⊆2U。集函数Pl:2U→[0, 1]称为U上的似然函数[19],如果
基于相同的概率指派函数,信任函数和似然函数是对偶的,即Bel(X)=~Pl(~X), 其中~X=U-X。
信任函数满足下列性质:
1) Bel(ø)=0;
2) Bel(U)=1;
3) 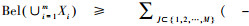
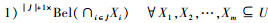
本节选取苗夺谦等[11]提出的4种乐观多粒度覆盖粗糙集模型。上述模型基于论域中极小描述或极大描述的交或并定义。
谭安辉等[22]指出,在信息系统中,集合的悲观多粒度近似可以由信度函数刻画,但是集合的乐观多粒度近似一般不具备这种特性。因而本文首先基于苗夺谦等[11]提出的4种乐观多粒度覆盖粗糙集模型定义悲观多粒度覆盖粗糙集模型。
对于给定的近似空间

定义10 令
 |
定义11 令
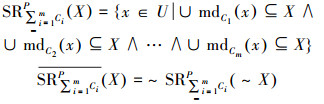 |
x的极大描述包含近似空间中所有与x相关的对象,当讨论近似空间
定义12 令
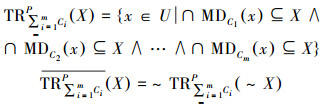 |
定义13 令
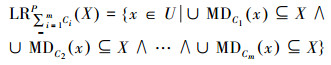 |
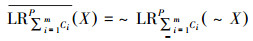 |
显然,如果C是U上的一族划分,上述4种多粒度覆盖粗糙集模型将退化为经典悲观多粒度粗糙集模型。因此,上述4种模型是对经典多粒度粗糙集模型的推广,并且也是粗糙集模型和覆盖粗糙集模型的推广。
3 MGCRS与证据理论之间联系本节讨论证据理论和多粒度覆盖粗糙集之间的联系。由于基于信任结构所导出的信任函数和似然函数是度量多粒度覆盖粗糙集中上、下近似的基础,因此首先给出上述4种类型悲观多粒度覆盖粗糙集模型相应的信任函数和似然函数来度量集合的上、下近似(记作∇_j, ∇j(j=1, 2, 3, 4)。
下面假设P是一个平均概率分布,即∀X⊆U, P(x)=|X|×|U|-1, |·|是集合的势。
定义14 令S=(U, A)为信息系统,C={C1, C2, …, Cm}是U上一族覆盖,∀x∈U, 用∇ij(x)(i=1, 2, …, m; j=1, 2, 3, 4)分别表示∩mdci(x)、∪mdci(x)、∩MDci(x)、∪MDci(x), 称∇j(x)=∪{∇ij(x)|i=1, 2, …, m; j=1, 2, 3, 4}为x关于覆盖族C的多元覆盖。
∀X⊆U,x∈U,X在上述4种悲观多粒度覆盖粗糙集模型中上、下近似的定义分别基于论域中x极小描述或极大描述的交或并所得x的相关元。因为X定义于多粒度环境中,所以无论x的极小描述还是x的极大描述均同时与覆盖C1, C2, …, Cm相关。即∀j∈{1, 2, 3, 4}如果集合{(∇ij(x))i=1, 2, …, m}中所有元均为X子集,则x属于∇_jX, 如果至少存在一个∇ij(x)与X相交不为空,则x属于∇j(X)。鉴于此, ∀x∈U, 本文对集族{∇ij(x)|i=1, 2, …, m}取并集后得∇j(x),∇j(x)是论域U上一个单粒度覆盖,从而悲观多粒度覆盖粗糙集转化为单粒度覆盖粗糙集。进一步,定理1借助关系划分函数,将覆盖与划分建立联系,将覆盖粗糙集转化为经典粗糙集,进而在定理2中得出证据理论与多粒度悲观覆盖粗糙集之间联系。
定理1 令U为论域,C为U上覆盖,∀x∈U, j∈{1, 2, 3, 4}, 定义关系划分函数fj:C→U, fj(X)={x∈U|X=∇j(x), j=1, 2, 3, 4}, ∀x∈U, 则fj(X)是U上的一个划分。
证明 ∀j∈{1, 2, 3, 4}, 首先须证,∀X, X′⊆U, X≠X′, 有fj(X)∩fj(X′)≠ø成立。
假设,∃x∈U, 使x∈fj(X)∩fj(X′),则有∇j(x)=X=X′成立,与X≠X′矛盾。∴∀X, X′⊆U, X≠X′, fj(X)∩fj(X′)=ø成立。
其次须证,有U=∪X⊆Ufj(X)成立。
∀x∈U,有x∈fj(∇j(x)),∇j(x)≠ø, ∇j(x)⊆U, 则∪X⊆Ufj(X)=U成立。
由划分定义知,fj(X)为U上划分。
定理2 令S=(U, A)为信息系统,C={C1, C2, …, Cm}是U上一族覆盖。∀X⊆U, x∈U, 概率指派函数m:2U→[0, 1]定义如下:
 |
式中:∇j*={∇j(x)|x∈U, j=1, 2, 3, 4},则U上相应的信任函数Bel∇jX和似然函数Pl∇jX为
 |
证明 ∀j=1, 2, 3, 4
1) ∀X⊆U, 显然有U=∪∑X⊆Uf(X)。则
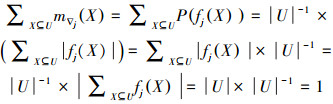 |
2)下证Bel∇j(X)=P(∇_j(X))
 |
进一步,可证∇j(x)⊆X
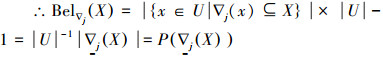 |
同理可证,Pl∇j(X)=P(∇j(X))。
其中, j=1, 2, 3, 4代表用相应信度函数分别刻画4种多粒度覆盖粗糙集的近似。
下面用例子进一步解释其具体含义。
例1 考虑一个房子的评价问题。设U={x1, x2, …, x6}是6所房子的集合,令A={公摊面积,颜色,价格,环境}是属性集合,B={购买意见}是决策集合。“公摊面积”的属性值是{较大,普通,较小},“颜色”的属性值是{优,良,差},“价格”的属性值是{高,中,低},“环境”的属性值是{安静,较吵,很吵},“购买意见”的决策值是{支持,中立,反对}。有3个专家{甲,乙,丙}对6所房子进行评价,他们的评价结果互相独立。评价结果列于表 1。
| U | 公摊面积 | 颜色 | 价格 | 环境 | 购买意见 |
| x1 | {较大,普通} | {优} | {高} | {安静} | {支持,中立} |
| x2 | {较大,普通} | {良} | {高,中,低} | {安静,较吵} | {支持,中立,反对} |
| x3 | {较大,普通} | {优,良} | {中,低} | {较吵,很吵} | {中立,反对} |
| x4 | {普通} | {差} | {低} | {很吵} | {中立} |
| x5 | {普通} | {差} | {中} | {很吵} | {反对} |
| x6 | {普通,较小} | {优,良} | {高,低} | {很吵} | {支持,反对} |
由属性集A诱导出的一族覆盖C={Ci, i=1, 2,…, 4}和等价关系R={Ri, i=1, 2,…, 4}及由决策集B诱导出覆盖的C5,如下:C1={{x1, x2, x3}, {x1, x2, x3, x4, x5, x6}, {x6}}, C2={{x1, x3, x6}, {x2, x3, x6},{x4, x5}},C3={{x1, x2, x6}, {x2, x3, x5},{x2, x3, x4, x6}}, C4={{x1, x2}, {x2, x3},{x3, x4, x5, x6}}, C5={{x1, x2, x6}, {x1, x2, x3, x4}, {x2, x3, x5, x6}}, R1={{x1, x2, x3},{x4, x5}, {x6}}, R2={{x1}, {x2}, {x3, x6},{x4, x5}}, R3={{x1}, {x2}, {x3}, {x4}, {x5}, {x6}}, R4={{x1}, {x2}, {x3}, {x4, x5, x6}}
选定专家决策D1={x1, x2, x6}, 用信任函数和似然函数刻画决策D1在经典悲观多粒度粗糙集模型和四型悲观多粒度覆盖粗糙集模型中的信任区间及不确定性,为用户做购买决定提供不同参考意见。
1) 对∀xt∈U, t∈{1, 2,…, 6}。
①∇i1(xt)=∩mdCi(xt), i∈1, 2, 3, 4。
 |
②∇1(xt)=∪{∇i1(xt)|i=1, 2, …, m},则
 |
 |
是关于覆盖族C的多粒度覆盖。
③由关系划分函数知,{x1, x2, x3, x6}=f1(∇1(x1)=∇1(x2)=∇1(x3)), f1(∇1(x4))=(∇1(x5))=U, f1(∇1(x6))=U-{x1}, 所以{{x1, x2, x3}, {x4, x5}, {x6}}是U上一个划分。
根据第1型模型知,∇_1(D1)={{x6}}, ∇1(D1)={{x6}, x1, {x2, x3}}。U上焦元为{{x1, x2, x3}, {x4, x5}, {x6}}, 其概率指派函数值分别为m({x6})=6-1,m({x1, x2, x3})=2-1, m({x4, x5})=3-1。
相应的信任函数和似然函数值为,Bel∇1(D1)=P(∇_1(D1))=6-1, Pl∇1(X)=P(∇1(X))=2×3-1。则专家决策D1在第一型悲观多粒度覆盖粗糙集模型中的信任区间为[6-1, 2×3-1],其不确定性为2×3-1-6-1=2-1。R中,D1的近似集为ø、U, 则相应信任区间为[0, 1]
显然,本文所提出的模型相较于经典多粒度粗糙集模型,更具实际应用价值。
2) j=2, 3, 4时,分别有∇i1(x)=∪mdci(x), ∩MDci(x), ∪MDci(x), i∈{1, 2, 3, 4}。计算过程与1)相似,本文不再一一计算。
4 结论经过上述讨论,本文得出以下结论:
1) 通过对现有多粒度覆盖粗糙集模型进行分析,构造了4种悲观多粒度覆盖粗糙集模型,以使其能够与证据理论更好地结合;
2) 基于集合的交、并运算和关系划分函数,实现了悲观多粒度覆盖粗糙集到单粒度多元覆盖粗糙集再到单粒度经典粗糙集的转化,进而实现简化上述4种模型的目的;
3) 结合证据理论,刻画了上述模型的近似及其不确定性。
在后续研究中,可以进一步给出基于信任函数和似然函数的多粒度覆盖粗糙集属性约简算法。
| [1] | PALAWK Z. Rough set[J]. International journal of computer & information sciences , 1982, 11 (5) : 341-356 |
| [2] | CHEN Degang, KWONG S, HE Qiang, et al. Geometrical interpretation and applications of membership functions with fuzzy rough sets[J]. Fuzzy sets and systems , 2012, 193 : 122-135 DOI:10.1016/j.fss.2011.07.011 |
| [3] | LIANG Jiye, CHIN K S, Dang Chuangyin, et al. A new method for measuring uncertainty and fuzziness in rough set theory[J]. International journal of general systems , 2002, 31 (4) : 331-342 DOI:10.1080/0308107021000013635 |
| [4] | LIANG Jiye, WANG Feng, DANG Chaungyin, et al. A group incremental approach to feature selection applying rough set technique[J]. IEEE transactions on knowledge and data engineering , 2014, 26 (2) : 294-308 DOI:10.1109/TKDE.2012.146 |
| [5] | TAN Anhui, LI Jinjin, LIN Guoping. Extended results on the relationship between information systems[J]. Information sciences , 2015, 290 : 156-173 DOI:10.1016/j.ins.2014.08.038 |
| [6] | BONIKOWSKI Z, BRYNIARSKI E, WYBRANIEC-SKARDOWSKA U. Extensions and intentions in the rough set theory[J]. Information sciences , 1998, 107 (1/2/3/4) : 149-167 |
| [7] | FENG Tao, MI Jusheng, WU Weizhi. Covering-based generalized rough fuzzy sets[M]//WANG Guoying, PETERS J F, SKOWRON A, et al. Rough Sets and Knowledge Technology. Berlin Heidelberg:Springer, 2006:208-215. |
| [8] | QIAN Y H, LIANG J Y. Rough set method based on multi-granulations[C]//Proceedings of the 5th IEEE International Conference on Cognitive Informatics. Beijing:IEEE, 2006:297-304. |
| [9] | 徐伟华, 刘士虎, 张文修. 一般二元关系下信息系统知识的粒度描述[J]. 计算机工程与应用 , 2011, 47 (18) : 40-44 XU Weihua, LIU Shihu, ZHANG Wenxiu. Granularity representation of knowledge in information system based on general binary-relation[J]. Computer engineering and applications , 2011, 47 (18) : 40-44 |
| [10] | QIAN Yuhua, LIANG Jiye, YAO Yiyu, et al. MGRS:a multi-granulation rough set[J]. Information sciences , 2010, 180 (6) : 949-970 DOI:10.1016/j.ins.2009.11.023 |
| [11] | LIU Caihui, MIAO Duoqian, QIAN Jin. On multi-granulation covering rough sets[J]. International journal of approximate reasoning , 2014, 55 (6) : 1404-1418 DOI:10.1016/j.ijar.2014.01.002 |
| [12] | DEMPSTER A P. Upper and lower probability inferences based on a sample from a finite univariate population[J]. Biometrika , 1967, 54 (3/4) : 515-528 DOI:10.2307/2335042 |
| [13] | SHAFER G. A mathematical theory of evidence[J]. Technometrics , 1978, 20 (1) : 242 |
| [14] | LIN Guoping, LIANG Jiye, QIAN Yuhua. An information fusion approach by combining multigranulation rough sets and evidence theory[J]. Information sciences , 2015, 314 : 184-199 DOI:10.1016/j.ins.2015.03.051 |
| [15] | 林国平. 覆盖广义粗糙集与信任函数[J]. 漳州师范学院学报:自然科学版 , 2010 (2) : 1-4 LIN Guoping. Connections between covering generization rough set and dempster-shafer theory of evidence[J]. Journal of Zhangzhou normal university:natural science , 2010 (2) : 1-4 |
| [16] | WU Weizhi, MI Jushneg. Knowledge reduction in incomplete information systems based on dempster-shafer theory of evidence[M]//WANG Guoying, PETERS J F, SKOWRON A, et al. Rough Sets and Knowledge Technology. Berlin Heidelberg:Springer, 2006:254-261. |
| [17] | YAO Y Y, LINGRAS P J. Interpretations of belief functions in the theory of rough sets[J]. Information sciences , 1998, 104 (1/2) : 81-106 |
| [18] | CHEN Degang, ZHANG Xiaoxia, LI Wanlu. On measurements of covering rough sets based on granules and evidence theory[J]. Information sciences , 2015, 317 : 329-348 DOI:10.1016/j.ins.2015.04.051 |
| [19] | CHEN Degang, LI Wanlu, ZHANG Xiao, et al. Evidence-theory-based numerical algorithms of attribute reduction with neighborhood-covering rough sets[J]. International journal of approximate reasoning , 2014, 55 (3) : 908-923 DOI:10.1016/j.ijar.2013.10.003 |
| [20] | WU Weizhi, LEUNG Y, ZHANG Wenxiu. Connections between rough set theory and Dempster-Shafer theory of evidence[J]. International journal of general systems , 2002, 31 (4) : 405-430 DOI:10.1080/0308107021000013626 |
| [21] | 吴伟志, 米据生, 李同军. 无限论域中的粗糙近似空间与信任结构[J]. 计算机研究与发展 , 2012, 49 (2) : 327-336 WU Weizhi, MI Jusheng, LI Tongjun. Rough approximation spaces and belief structures in infinite universes of discourse[J]. Journal of computer research and development , 2012, 49 (2) : 327-336 |
| [22] | TAN Anhui, WU Weizhi, LI Jinjin, et al. Evidence-theory-based numerical characterization of multi-granulation rough sets in incomplete information systems[J]. Fuzzy sets and systems , 2016, 294 : 18-35 DOI:10.1016/j.fss.2015.08.016 |
| [23] | ZAKOWSKI B W. Approximations in the space (u, π)[J]. Demonstratio mathematica , 1983, 16 (3) : 761-769 |



