粗糙集理论[1-2]最早由波兰数学家Pawlak于1982年提出,是数据分析的一种数学工具,是经典集合论的一种推广形式,其主要思想是在保持分类不变的情况下,经过属性约简推出问题的决策准则。目前,国内对粗糙集的理论基础及应用[3-4]研究取得了很大的进步,许多学者已在该领域出版了相应的专著,同时也发表了数百篇的论文。当然粗糙集的应用[5-6]不仅仅是限制在知识理论方面,它也在人工智能、故障检测、数据挖掘、地震预报、数据分析、模式识别、智能信息处理等领域得到了普遍的应用。众所周知,粗糙集理论的核心问题之一就是知识约简[7-9]。约简就是知识库中所描述的知识的属性并不都是同等重要的,甚至有些属性是多余的。所谓知识约简,就是从知识库中去掉一些不重要的属性,使得知识得以简化, 又不丢失其主要信息。
在粗糙集理论中,信息系统[10]是对知识进行表达的重要工具。常常因为信息系统的复杂性和不确定性,事物的属性值难以用精确的数值来表达,而是采用模糊区间形式[11-12]表示,本文就这一问题引进了一种优势关系[13-15],在此基础上建立不协调的区间值模糊决策序信息系统[15]。在不协调的区间值模糊序信息系统中引进了部分一致约简[16]的函数,得到部分一致约简的判定定理以及辨识属性集和辨识矩阵, 提供了不协调的区间值模糊序信息系统的部分一致约简的具体方法, 同时通过例子验证此方法的有效性, 丰富了区间值模糊决策序信息系统中的粗糙集方法。
1 基于区间值模糊的决策序信息系统决策信息系统是既有条件属性又有决策属性的一种特殊信息系统。决策信息系统主要是研究条件属性和决策属性之间的关系问题。为了便于理解,下面先给出一些基本概念。
定义1[15] 称一个四元组I=(U, AT∪DT, F, G)为一个决策信息系统,其中I=(U, AT, F)是信息系统,AT称为条件属性集,DT称为目标属性集,其中:U是有限对象集,U={x1, x2, …, xn};
AT是有限条件属性集,AT={a1, a2, …, ap};
DT是有限决策属性集,DT={d1, d2, …, dq};
F是U与AT的关系集,其中F={f:U→Va, a∈DT},Va为a的有限值域;
G是U与DT的关系集,其中G={g:U→Vd, d∈DT},Vd为d的有限值域。
设I=(U, AT∪DT, F, G)为一个决策信息系统,若对任意f∈F,a∈AT和xi∈U都有
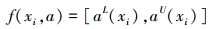 |
则称I=(U, AT, F)为区间值模糊信息系统,I=(U, AT∪DT, F, G)为区间值模糊决策信息系统。其中:aL(xi), aU(xi)∈[0,1]并且有aL(xi)≤aU(xi),f(xi, a)是xi在属性a下的属性值范围(区间数)。特别地,当aL(xi)≡aU(xi)的时候,f(xi, a)就退化成了一个模糊数。因此区间值模糊信息系统是一般形式,单值模糊信息系统是其特殊形式。
设I=(U, AT, F)为区间值模糊信息系统。对任意的a∈AT,在区间值模糊信息系统中可对属性值进行比较,定义
 |
式中:“≤”和“≥”可在区间值模糊信息系统中分别构建一个递增的偏序和一个递减的偏序。如果区间值模糊信息系统中属性的值域为递增的或者递减的偏序,那么称该属性是区间值模糊信息系统中的一个准则。本文中只考虑由递增偏序构成的优势关系的情景,递减的偏序情形可以类似地得到相同的结论。
定义2 设I=(U, AT∪DT, F, G)为区间值模糊决策信息系统,若I中所有条件属性都是准则,则称I是区间值模糊决策序信息系统,记作I≥。称I≥=(U, AT, F)为区间值模糊序信息系统。
在区间值模糊序信息系统中,设a∈AT为准则,存在优势关系“≥a”,“xj≥axi”表示xj关于准则a优于xi。设A⊆AT是准则集,那么xj≥Axi
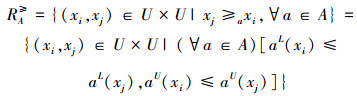 |
由区间值模糊优势关系RA≥诱导的[xi]A≥为
 |
称为区间值模糊优势类,简称为优势类。用U/RA≥={[x]A≥|x∈U}表示论域U上由区间值模糊优势关系RA≥诱导的区间值模糊优势类全体。一般地,U/RA≥中的优势类不一定构成U上的一个划分,而是仅仅构成U上的一个覆盖。
定义3 设I≥=(U, AT∪d, F, G)为区间值模糊决策序信息系统,如果RAT≥⊆RDT≥,则称该区间值模糊决策序信息系统是协调的,否则为不协调的。
本文仅仅考虑比不协调区间值模糊决策序信息系统。
2 区间值模糊决策序信息系统的部分一致约简我们已经知道了序信息系统中属性约简理论定义的部分一致函数,下面将给出区间值模糊序信息系统中的部分一致函数的定义方式。
定义4 设I≥=(U, AT∪{d}, F, G)为区间值模糊单决策序信息系统。对于任意的A⊆AT,x∈U,记
 |
我们称δA(x)为论域U上关于准则集A的部分一致函数。
定义5 [15]设α=(a1, a2, …, an)和β=(b1, b2, …, bn)为两个n维向量,若ai=bi(i=1, 2, …, n)称向量α等于向量β,记作α=β;若ai≤bi(i=1, 2, …, n)称向量α小于等于向量β,记作α≤β;否则如果存在某个i0, (i0∈{1, 2, …, n}),使得ai0>bi0,称向量α不小于等于向量β, 记作α≮β。
显然由以上定义可立即得到下面命题。
定理1 设I≥=(U, AT∪d, F, G)为区间值模糊决策序信息系统。对于任意的A⊆AT,
1) 对∀x∈U,当B⊆A时,有δB(x)⊆δA(x);
2) 对∀x, y∈U,当[y]A≥⊆[x]A≥时,有δA(x)⊆δA(y)。
定义6 设I≥=(U, AT∪d, F, G)为区间值模糊决策序信息系统。A⊆AT,对于任意的x∈U,如果有δA(x)=δAT(x),则称A是I≥中关于区间值模糊优势关系RAT≥的部分一致协调集,如果A的任何真子集均不是部分一致协调集,则称A是I≥中关于区间值模糊优势关系RAT≥的部分一致约简。
下面具体给出区间值模糊决策序信息系统的部分一致约简的判定定理。
定理2 设I≥=(U, AT∪d, F, G)为区间值模糊决策序信息系统,A⊆AT,则A是部分一致协调集当且仅当对∀x, y∈U, 若δAT(x)∩δA(y)≠δAT(y),则[x]A≥∩[y]A≥≠[y]A≥。
证明 必要性。反证法。假设当δAT(x)∩δAT(y)≠δAT(x)时有[x]A≥∩[y]A≥≠[y]A≥不成立,此时[x]A≥∩[y]A≥=[y]A≥则有[y]A≥⊆[x]A≥,由定理1可知δA(x)⊆δA(y)。由A是部分一致协调集得δAT(x)⊆δAT(y),即有δAT(x)∩δAT(y)=δAT(x),矛盾。必要性成立。
充分性。由定理1知δA(x)⊆δAT(x),只证δAT(x)⊆δA(x)即可。对∀x, y∈U,如果δAT(x)∩δAT(y)≠δAT(x),则[x]A≥∩[y]A≥≠[y]A≥。因此对∀x, y∈U,若[x]A≥∩[y]A≥=[y]A≥,则δAT(x)∩δAT(y)=δAT(x),即[y]A≥⊆[x]A≥成立推出δAT(x)⊆δAT(y)成立。
任取Dk∈δAT(x),需证[x]A≥⊆Dk。不妨设y∈[x]A≥,则有[y]A≥⊆[x]A≥,可得δAT(x)⊆δAT(y)。因此Dk∈δAT(y),即[y]AT≥⊆Dk,于是y∈Dk,由y的任意性可得[x]A≥⊆Dk从而σAT(x)⊆σA(x)成立,充分性得证。
3 区间值模糊决策序信息系统的部分一致约简方法第3节中给出了不协调的区间值模糊决策序信息系统的部分一致协调集,这是判断准则集是否协调的理论所在,这节介绍部分一致约简的方法,先给出辨识属性集以及辨识属性矩阵的相关概念。
定义7 设I≥=(U, AT∪d, F, G)为区间值模糊序信息系统,记
 |
称Dis≥ATδ(xi, xj)为I≥中xi, xj关于区间值模糊优势关系RAT≥的部分一致可辨识属性集。记
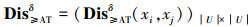 |
称Dis≥ATδ为I≥中xi, xj关于区间值模糊优势关系RAT≥的部分一致可辨识矩阵。特别地,对任意xi, xj∈U有
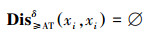 |
定理3 设I≥=(U, AT∪d, F, G)为区间值模糊决策序信息系统,A⊆AT,A是部分一致协调集当且仅当对任意(x, y)∈D≥ATδ都有A∩Dis≥ATδ(x, y)≠Ø。
证明 必要性。对任意(x, y)∈D≥ATδ,有σAT(y)⊂σAT(x),则σAT(x)∩σAT(y)≠σAT(x)。因A是部分一致协调集,由定理2得[x]A≥∩[y]A≥≠[y]A≥,因此[x]A≥与[y]A≥的关系有3种情况:
1) [x]A≥⊂[y]A≥;
2) I≥=(U, AT∪d, F, G);
3) [x]A≥∩[y]A≥⊂[x]A≥且[x]A≥∩[y]A≥⊂[y]A≥。
下证3种情况下均有A∩Dis≥ATδ(x, y)≠Ø成立。
1) 如果[x]A≥⊂[y]A≥则至少存在一个z∈[y]A≥,但z∉[x]A≥,由z∉[x]A≥可知,至少存在一个a∈A,使得f(x, a)>f(y, a)。因为z∈[y]A≥, 所以f(y, a)≤f(z, a)。于是得到f(x, a)>f(y, a), 因此a∈Dis≤ATδ(x, y),即有A∩Dis≤ATδ(x, y)≠Ø。
2) 如果[x]A≥∩[y]A≥=Ø,必然至少存在一个a∈A使得f(x, a)>f(y, a),即A∩Dis≤ATδ(x, y)≠Ø。否则,若对于所有的a∈A都有f(x, a)≤f(y, a),则y∈[x]A≥,与[x]A≥∩[y]A≥=Ø矛盾。
3) 如果[x]A≥∩[y]A≥⊂[x]A≥且[x]A≥∩[y]A≥⊂[y]A≥,证明与(1)相同。因为此时也至少存在一个z∈[y]A≥,但是z∉[x]A≥。由此必要性即证。
充分性。如果对所有的(x, y)∈Dis≤ATδ有A∩Dis≤ATδ(x, y)≠Ø,则必定存在a∈A并且有a∈Dis≤ATδ(x, y),故有f(x, a)>f(y, a),所以y∉[x]A≥。因此xB≥∩yB≥≠yB≥。另外,由(x, y)∈Dis≤ATδ,得δAT(x)⊃δAT(y),于是δAT(x)∩δAT(y)≠δAT(x)。当δAT(x)∩δAT(y)≠δAT(x)时有[x]A≥∩[y]A≥≠[y]A≥。由定理2知A是部分一致协调集,充分性得证。
定义8 设I≥=(U, AT∪d, F, G)为区间值模糊决策序信息系统,部分一致可辨识矩阵为Dis≥ATδ。称
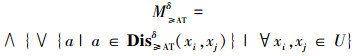 |
为该区间值模糊决策序信息系统的部分一致可辨识公式。
定理4 设Ø为区间值模糊决策序信息系统,部分一致可辨识公式M≤ATδ的极小析取范式为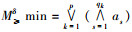
实例分析 设I≥=(U, AT∪d, F, G)为区间值模糊序决策信息系统,U={x1, x2, …, x6}为论域,代表 6个投资对象,A={a1, a2, a3},分别代表着市场风险、技术风险、管理风险,d为决策属性,表示风险,其中3表示“高”,2表示“中”,1表示“低”,统计数据如表 1所示。
| U | a1 | a2 | a3 | d |
| x1 | [0.1, 0.3] | [0.2, 0.3] | [0.1, 0.4] | 3 |
| x2 | [0.3, 0.5] | [0.2, 0.6] | [0.2, 0.8] | 2 |
| x3 | [0.1, 0.5] | [0.1, 0.4] | [0.2, 0.7] | 1 |
| x4 | [0.2, 0.7] | [0.1, 0.5] | [0.3, 0.7] | 2 |
| x5 | [0.3, 0.6] | [0.3, 0.7] | [0.2, 0.9] | 3 |
| x6 | [0.3, 0.9] | [0.2, 0.7] | [0.3, 0.8] | 1 |
由表 1可得到
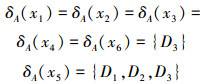 |
显然,RA≥Rd≥。因此该区间值模糊序决策信息系统是不协调的。
对于表 1给出的关于风险投资的区间值模糊序决策信息系统,求部分一致约简。
情形1 利用定义6求解。
在该系统中记
 |
由部分一致函数δA(x)定义可得
 |
当取B={a2, a3}时,容易验证对于∀x∈U有:[x]A≥=[x]B≥,因此有δB(x)=δA(x)。故B={a2, a3}是部分一致协调集。
当取B′={a1, a3}有
 |
 |
于是
 |
因此对于∀x∈U有δB′(x)=δA(x)。B′={a1, a3}是部分一致协调集。
当取B″={a1, a2}时有
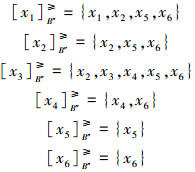 |
则有
 |
对于∀x∈U有δB″(x)=δA(x)。故B″={a1, a2}也是部分一致协调集。
进一步可以计算{a2、a3}均是部分一致协调集,并且可以计算出,{a1}不是部分一致协调集。因此该区间值模糊决策序信息系统有两个部分一致约简,即{a2}和{a3}。
情形2 利用定理3求解。
可以计算该信息系统的部分一致可辨识矩阵如表 2所示。
| Dis≥Aμ | x1 | x2 | x3 | x4 | x5 | x6 |
| x1 | Ø | Ø | Ø | Ø | Ø | Ø |
| x2 | Ø | Ø | Ø | Ø | Ø | Ø |
| x3 | Ø | Ø | Ø | Ø | Ø | Ø |
| x4 | Ø | Ø | Ø | Ø | Ø | Ø |
| x5 | A | A | A | A | Ø | a2, a3 |
| x6 | Ø | Ø | Ø | Ø | Ø | Ø |
由定义8可得
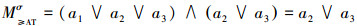 |
因此{a2}和{a3}是该区间值模糊决策序信息系统的所有部分一致约简。
上述情形1和情形2所求得的结果是一致的,显然在该决策问题中技术和管理风险因子是对象的肯定决策不变的属性。两种求解方法不同,所费的时间不一样。从求解过程来看,情形1过程较复杂,相对情形2时间较少,因此在求部分一致约简时,利用情形2求解具有明显的时间优势。
5 结论本文针对区间值模糊序决策信息系统的条件属性与决策属性的不协调性,着重研究了改系统的部分一致约简。主要取得如下结论:
1) 通过分析部分一致约简的性质得到了对应的判定定理;
2) 在上述基础上建立了辨识矩阵,给出了获取部分一致约简的具体方法,并且用两种情形对实例进行了对比分析。
3) 通过比较可以知道,本文对部分一致约简进行了更精确地刻画,可以简化在时间上的求解过程。
| [1] | PAWLAK Z. Rough sets:theoretical aspects of reasoning about data[M]. Boston: Kluwer Academic Publishers, 1991 . |
| [2] | PAWLAK Z, GRZYMALA-BUSSE J, SLOWINSKI R, et al. Rough sets[J]. Communications of the ACM , 1995, 38 (11) : 89-95 |
| [3] | 王珏, 苗夺谦, 周育健. 关于Rough Set理论与应用的综述[J]. 模式识别与人工智能 , 1996, 9 (4) : 337-344 WANG Jue, MIAO Duoqian, ZHOU Yujian. Rough set theory and its application:a survey[J]. Pattern recognition and artificial intelligence , 1996, 9 (4) : 337-344 |
| [4] | 苗夺谦, 王珏. 基于粗糙集的多变量决策树构造方法[J]. 软件学报 , 1997, 8 (6) : 425-431 MIAO Duoqian, WANG Jue. Rough sets based approach for multivariate decision tree construction[J]. Journal of software , 1997, 8 (6) : 425-431 |
| [5] | 张小红, 裴道武, 代建华. 模糊数学与Rough集理论[M]. 北京: 清华大学出版社, 2013 . ZHANG Xiaohong, PEI Daowu, DAI Jianhua. Fuzzy mathematics and the rough set theory[M]. Beijing: Tsinghua University Press, 2013 . |
| [6] | 徐伟华, 张先韬, 王巧荣. 序信息系统中变精度粗糙集属性约简的MATLAB实现[J]. 重庆理工大学学报:自然科学版 , 2013, 27 (1) : 107-115 XU Weihua, ZHANG Xiantao, WANG Qiaorong. Experimental computing on attribute reduction by Matlab in dominance-based variable precision rough set[J]. Journal of Chongqing university of technology:natural science , 2013, 27 (1) : 107-115 |
| [7] | 张文修, 米据生, 吴伟志. 不协调目标信息系统的知识约简[J]. 计算机学报 , 2003, 26 (1) : 12-18 ZHANG Wenxiu, MI Jusheng, WU Weizhi. Knowledge reductions in inconsistent information systems[J]. Chinese journal of computers , 2003, 26 (1) : 12-18 |
| [8] | 徐伟华, 张文修. 基于优势关系下不协调目标信息系统的知识约简[J]. 计算机科学 , 2006, 33 (2) : 182-184 XU Weihua, ZHANG Wenxiu. Knowledge reductions in inconsistent information systems based on dominance relations[J]. Computer science , 2006, 33 (2) : 182-184 |
| [9] | 韦碧鹏, 吕跃进, 李金海. 优势关系下粗糙集模型的属性约简[J]. 智能系统学报 , 2014, 9 (2) : 251-258 WEI Bipeng, LV Yuejin, LI Jinhai. attribute reduction based on the rough set model under α dominance relation[J]. CAAI transactions on intelligent systems , 2014, 9 (2) : 251-258 |
| [10] | 张文修, 梁怡, 吴伟志. 信息系统与知识发现[M]. 北京: 科学出版社, 2003 . ZHANG Wenxiu, LIANG Yi, WU Weizhi. Information system and knowledge discovery[M]. Beijing: Science Press, 2003 . |
| [11] | 张楠, 苗夺谦, 岳晓冬. 区间值信息系统的知识约简[J]. 计算机研究与发展 , 2010, 47 (8) : 1362-1371 ZHANG Nan, MIAO Duoqian, YUE Xiaodong. Approaches to knowledge reduction in interval-valued information system[J]. Journal of computer research and development , 2010, 47 (8) : 1362-1371 |
| [12] | 于莹莹, 曾雪兰, 孙兴星. 优势关系下的区间值信息系统及其属性约简[J]. 计算机工程与应用 , 2011, 47 (35) : 122-124 YU Yingying, ZENG Xuelan, SUN Xingxing. Interval-valued information system based on dominance relation and its attribute reduction[J]. Computer engineering and applications , 2011, 47 (35) : 122-124 |
| [13] | GRECO S, MATARAZZO B, SLOWINSKI R. Rough approximation of a preference relation by dominance relations[J]. European journal of operational research , 1999, 117 (1) : 63-83 DOI:10.1016/S0377-2217(98)00127-1 |
| [14] | 徐伟华, 张文修. 基于优势关系下的协调近似空间[J]. 计算机科学 , 2005, 32 (9) : 164-165 XU Weihua, ZHANG Wenxiu. Consistent approximation spaces based on dominance relations[J]. Computer science , 2005, 32 (9) : 164-165 |
| [15] | 徐伟华. 序信息系统与粗糙集[M]. 北京: 科学出版社, 2013 . XU Weihua. Ordered information systems and rough sets theory[M]. Beijing: Science Press, 2013 . |
| [16] | 徐伟华, 张晓燕, 张文修. 优势关系下不协调目标信息系统的部分一致约简[J]. 模糊系统与数学 , 2009, 23 (6) : 155-161 XU Weihua, ZHANG Xiaoyan, ZHANG Wenxiu. Partially consistent reduction in inconsistent information systems based on dominance relations[J]. Fuzzy systems and mathemATics , 2009, 23 (6) : 155-161 |



