利用测得的动态数据进行结构损伤识别是结构健康监测的重要环节,传感器位置的选择对损伤识别结果有重要影响[1],现存的一些损伤识别方法在进行振动测试时,一般根据工程经验在结构上均匀布置传感器[2],或采用分步式的布置方式测量模型全部节点上的动态响应[3],需要测点较多,测试方案复杂。传感器优化布置就是将传感器布置在结构信息最丰富的位置,用尽量少的传感器获得尽可能多的结构状态信息,以便在噪声环境下准确识别结构参数,及时发现结构损伤。
进行传感器优化布置时,首先要确定传感器优化布置的准则,其次设计相适应的优化算法。目前常用的优化准则有模态保证准则[4]、模态动能法[5-6],模型缩减法[7]、Fisher信息准则[8]等。李东升等[9]对上述方法进行了综述,并分析了不同方法之间数学本质上的内在联系与差异。其中,基于Fisher信息矩阵的传感器优化布置策略在现今发展较为成熟,通过最大化Fisher信息矩阵的某一范数实现传感器位置的优化。Kammer[10]将信息阵准则应用于结构模态识别的传感器布置问题,提出了有效独立法,通过最大化信息阵的行列式来逐步消除对目标模态向量线性无关贡献最小的自由度。Kammer等[11]还提出了三维方向的有效独立法,实现了对多维传感器的优化布置;Yi等[12]结合有效独立法和模态保证准则提出了一种新的多维传感器优化布置准则,并引入狼群算法提高了计算效率;Castro等[13]将有效独立法应用到木结构中,在考虑材料参数的不确定性的情况下实现了传感器位置的优化;为了准确测量结构的中频振动特性,Nimityongskul等[14]对结构频响函数进行主成分分析得到主方向,以各主方向对应的频率响应作为估计目标,构造Fisher信息矩阵,实现了基于频率响应的有效独立法;Friswell等[15]证明了当布置较多数量的传感器时,采用有效独立法得到的传感器布置方案会出现测点局部聚集现象,从而不能保证目标模态的线性无关性;为了避免测点聚集产生的信息冗余问题,Li等[16]采用K-均值聚类算法,根据动态特性的相似程度对结构自由度进行归类,在每一类中分别确定传感器位置,得到空间分布较为合理的传感器布置方案。
在对损伤参数识别的传感器优化布置问题中,最大化Fisher信息矩阵的行列式得到的传感器优化测点集中于损伤参数敏感区,可以有效判定是否发生损伤,但空间距离较近的候选测点往往会提供重复的信息,测点集中产生信息冗余,不利于损伤定位[17]。为此,以反映信息独立程度的距离系数对候选自由度的Fisher信息矩阵进行加权修正,以修正后的有效Fisher信息阵行列式最大化为目标,采用逐步累加的方法确定传感器测点。采用该方法对一个16自由度剪切型弹簧质量模型进行传感器优化布置,并与传统Fisher信息准则下的传感器配置结果进行对比分析。
1 传感器优化布置问题的数学模型对于一个具有Nd个自由度的线性结构模型,其运动微分方程可以表示为
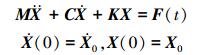 |
(1) |
式中:M, C, K∈RNd×Nd分别为质量矩阵、阻尼矩阵和刚度矩阵;
 |
(2) |
假设能够获得全部Nd个自由度上的结构响应:
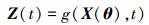 |
(3) |
式中:Z(t)∈RNd为测得响应,函数g(·) 表示测量过程。由于损伤识别的目的是准确识别结构损伤参数的变化,取式 (3) 的变分形式:
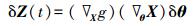 |
(4) |
式中: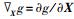
考虑噪声的影响,则有
 |
(5) |
式中:误差向量ε(t)∈RNd包含了测量噪声和模型误差,一般假定为方差为σ2的高斯白噪声,即ε~N(0, σ2INd)。
传感器优化布置就是以包含尽量多的损伤信息为条件,从结构模型的全部Nd个自由度中选择N0个位置作为传感器测点,这N0个位置的时程响应要对损伤的变化足够敏感。其选择过程表示为
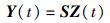 |
(6) |
式中:Y(t)∈为RN0个传感器的测量输出, S∈RN0×Nd为测量矩阵,是模型全部自由度到测量自由度的映射。用由0和1组成的Nd维向量p作为传感器布置向量,若p的第j个元素为1,表示在第j个自由度布置传感器,否则在该自由度不安装传感器, 则有
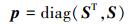 |
(7) |
对式 (6) 求差分后代入式 (5),可得
 |
(8) |
当测量函数gi(·) 与Xi成线性关系时,式 (8) 又可简化为
 |
(9) |
假定可以获得结构损伤参数的无偏估计量,根据Cramer-Rao不等式则有
 |
(10) |
式中: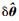
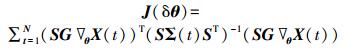 |
(11) |
式中:Σ(t) 为噪声ε(t) 的协方差矩阵。当测得的数据就是结构的响应时,G=INd,式 (11) 可简化为
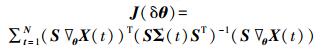 |
(12) |
达到Cramer-Rao下界的无偏估计量称为有效估计量,即式 (10) 的不等式变为等式:
 |
(13) |
由式 (13) 可以看出,最大化Fisher信息矩阵将使得估计误差的协方差矩阵最小化[8]。因此,传感器优化布置的目标就是选择适当的S,使得Fisher信息阵的某一种范数最大化,从而使结构损伤参数的估计误差尽可能小。
2.2 Fisher信息矩阵的计算从式 (12) 可以看出,Fisher信息矩阵计算的关键在于求得雅可比矩阵∇θX(t),即结构响应对损伤参数的灵敏度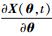
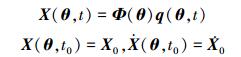 |
(14) |
式中:X0、
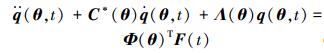 |
(15) |
式中:C*(θ)=diag (2ξ1ω1, 2ξ2ω2, …, 2ξNdωNd) 为模态阻尼矩阵;ξ1, ξ2, …, ξNd为阻尼比;Λ(θ)=diag (ω21, ω22, …, ωNd2), ω1, ω2, …, ωNd为模态固有频率。
式 (14) 两边对θ求偏导,得到
 |
(16) |
定义
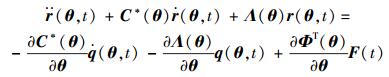 |
(17) |
假定初始条件r(θ,t0)=0, 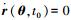

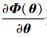
考虑结构全部自由度对应的Fisher信息矩阵:
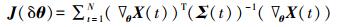 |
(18) |
令ai(t) 为雅可比矩阵∇θX(t) 的第i行,由于Σ(t) 为对角阵,可将Fisher信息矩阵表达为各个自由度贡献之和的形式,即
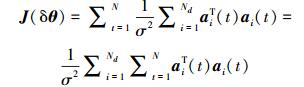 |
(19) |
式中σ2是一个常数,不会影响传感器优化布置结果,所以规定第k个自由度对应的Fisher信息矩阵为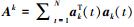
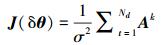 |
(20) |
如果有两个自由度所对应的Fisher信息矩阵是非常相似的,那么测量这两个自由度上的结构响应与仅测量其中一个自由度得到的信息量是基本相同的,即使这两个自由度对于结构损伤参数的估计都有很大的贡献。
采用欧氏距离来度量两个测点之间的信息阵的相似性[19]。根据定义,n维向量x=(x1, x2, …, xn) 和y=(y1, y2, …, yn) 之间的欧氏距离为d(x, y)= 
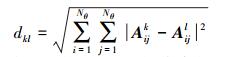 |
(21) |
式中信息矩阵的维数Nθ即为损伤参数θ中元素的数目。为了方便引入权重系数,对欧氏距离做标准化处理
 |
(22) |
式中:dmax为一组候选测点中最大的欧氏距离。
若用s表示已经选择的传感器测点集合,定义待选测点k对应的Fisher信息矩阵的距离系数为
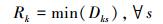 |
(23) |
利用Rk加权式 (20) 中的Fisher信息阵,得到新的有效信息阵, 即
 |
(24) |
以距离系数修正的有效Fisher信息矩阵范数最大化为目标的传感器布置准则,称为传感器优化布置的距离系数-Fisher信息准则。
4 距离系数-Fisher信息准则下的传感器优化布置算法本文以常用的行列式作为待优化的范数形式,采用逐步累加的方法[20]来实现距离系数-Fisher信息准则下的传感器优化布置,以得到同时满足损伤参数可识别和避免信息冗余的测点布置方案,从测量的Nd个自由度中选择N0个位置布设传感器,具体步骤如下。
1) 分别计算每个候选自由度对应的Fisher信息矩阵的行列式,记录行列式值最大的候选自由度,作为第一个测点位置。
2) 假设已经确定了m个测点位置,且m < N0,此时还剩余Nd-m个候选自由度。
①根据式 (21) 分别计算第m个测点与剩余Nd-m个候选自由度的信息阵之间的欧氏距离dkn,下标k表示第k个候选自由度,记录Nd-m个距离中的最大值dmax,并由式 (22) 得到标准化的欧氏距离Dkm。
②当m=1时,只有一个已选测点,所以Rk=Dk1;当m>1时,为保证式 (23) 成立,比较Rk和Dkm,若Dkm < Rk,则更新Rk=Dkm,否则Rk不变。
③将第k个候选自由度增加到已选测点集合中,计算该m+1个测点所对应的有效信息阵的行列式,计算公式为
 |
(25) |
遍历Nd-m个候选自由度,记录使Tkm+1最大的候选自由度作为第m+1个测点。
3) 重复2),确定剩余传感器布置位置,直至确定全部N0个测点位置,得到基于距离系数-Fisher信息准则的传感器优化布置方案。
5 数值算例以图 1所示的16自由度剪切型弹簧-质量模型为研究对象,将每个弹簧刚度的变化作为待识别参数。以位移传感器为例,分别运用传统Fisher信息准则和距离系数-Fisher信息准则进行传感器优化布置。

|
| 图 1 16自由度剪切型弹簧—质量模型 Fig. 1 16 DOFs shear type spring-mass model |
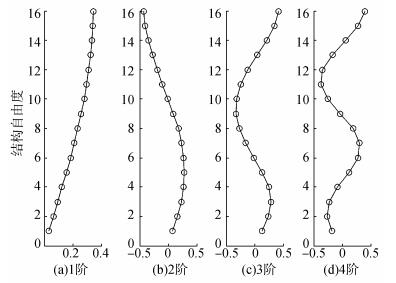
模型结构参数:m1~m4=5 kg,m5~m8=4 kg,m9~m12=3 kg,m13~m16=2 kg; k5~k8=700 N/m,k9~k12=600 N/m,k13~k16=500 N/m; 采用比例阻尼,各阶模态阻尼比均为0.02。图 2所示为模型前4阶振型。
|
| 图 2 模型前四阶振型 Fig. 2 First 4 mode shapes of the spring-mass model |
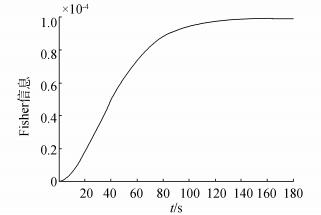
在试验之前,结构所受激励是未知的。由于可以利用自由振动响应重构结构的参数信息,因此通过在初始条件x16=0, 
|
| 图 3 δK1的Fisher信息 Fig. 3 Fisher information of δK1 |
求得结构响应对损伤参数的灵敏度矩阵∇θX(t)是计算Fisher信息矩阵的关键,可通过2.2节介绍的方法实现。在实际工程中,结构自由度数目巨大,为了提高计算效率,可选取振型灵敏度系数大的部分模态进行求解。
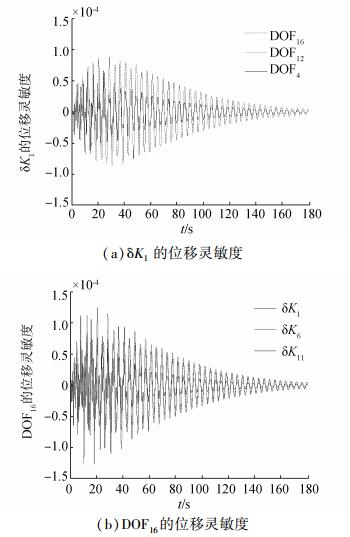
图 4(a)为自由度4、12、16上的位移响应对损伤参数δK1的灵敏度,可以看出,越靠近悬臂顶端的自由度,其位移响应对δK1越敏感,这一结论对其余损伤参数依然成立。图 4(b)显示了第16自由度上的位移响应对δK1、δK6、δK11的灵敏度,可见,损伤参数越靠近悬臂根部,第16自由度上的位移响应对其越敏感,悬臂的其他自由度位移变化也满足这一规律。
|
| 图 4 结构位移响应对损伤参数的灵敏度 Fig. 4 Sensitivity of structural displacements with respect to damage parameters |
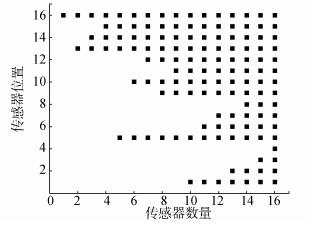
为方便分析,假定噪声协方差矩阵Σ=INd。采用逐步累加的方法[20],使Fisher信息矩阵的行列式最大化,得到基于传统Fisher信息准则的传感器优化布置方案如图 5所示。
|
| 图 5 基于传统Fisher信息准则的传感器优化布置方案 Fig. 5 Scheme of optimal sensor placement based on traditional Fisher information criterion |
Fisher信息矩阵包含结构响应对损伤参数的灵敏度信息,最大化Fisher信息阵的行列式得到的传感器测点满足对损伤参数的敏感性要求。在图 5中,测点分布于结构响应对损伤参数的敏感区,从而能够最大程度上发现损伤的发生,但测点在悬臂顶端聚集,并不满足损伤参数可观性的要求,即不利于损伤定位。根据工程经验,在实际布设传感器时,力求将传感器分散布置,避免局部过分集中现象[17]。
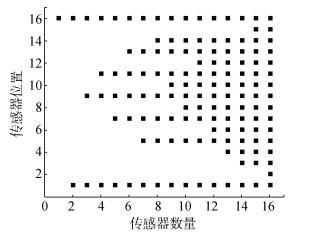
运用基于距离系数-Fisher信息准则的传感器布置方法,得到的传感器布置方案如图 6所示。
|
| 图 6 基于距离系数-Fisher信息准则的传感器优化布置方案 Fig. 6 Scheme of optimal sensor placement based on distance coefficient-Fisher information criterion |
由图 6可以看出,其测点分布更加分散,大部分测点位于悬臂上半部分对损伤参数较敏感的区域。当传感器数目较少时,测点之间能够保持一定的距离,避免了信息冗余问题,同时符合实际工程经验。
综上所述,基于距离系数-Fisher信息准则得到的传感器测点满足结构响应对损伤参数敏感性的要求,同时保证不同测点间的信息相互独立。
6 结论基于传统Fisher信息准则,采用距离系数修正Fisher信息矩阵,得到距离系数-Fisher信息准则。以一个16自由度剪切型弹簧-质量模型作为算例,比较分析传统Fisher信息准则和距离系数-Fisher信息准则下的传感器优化布置结果,得出以下结论:
1) Fisher信息准则通过使Fisher信息矩阵的范数最大化,使得估计误差的协方差矩阵最小,即最小化结构损伤参数的估计误差。
2) 基于传统Fisher信息准则的传感器布置方案中,测点聚集在结构响应对损伤参数的敏感区,产生信息冗余。
3) 基于距离系数-Fisher信息准则得出的传感器布置方案空间分布更加合理,测点大部分位于结构响应对损伤参数的敏感区,同时相互之间保持一定的距离,避免了信息冗余问题,在能够判定损伤发生的同时,有利于损伤定位。
4) 需要进一步深入研究,比较本文方法与其他传感器优化布置方法对实际结构的损伤识别效果。
| [1] | SHADAN F, KHOSHNOUDIAN F, ESFANDIARI A. A frequency response-based structural damage identification using model updating method[J]. Structural control & health monitoring, 2016, 23(2): 286-302. |
| [2] | 胡焕. 基于频响函数的动力学模型修正方法研究[D]. 上海: 上海交通大学, 2010. HU Huan. Investigation of dynamics model updating method based on FRF[D]. Shanghai: Shanghai Jiao Tong University, 2010. |
| [3] | 卢洋. 基于频响函数模式置信准则的桥梁损伤动力识别方法研究[D]. 北京: 北京交通大学, 2014. LU Yang. Study on dynamic identification method for bridge damage based on signature assuerance cretrion of frequency response functions[D]. Beijing: Beijing Jiaotong University, 2014. |
| [4] | HE Can, XING Jianchun, LI Juelong, et al. A new optimal sensor placement strategy based on modified modal assurance criterion and improved adaptive genetic algorithm for structural health monitoring[J]. Mathematical problems in engineering, 2015, 2015: 1-10. |
| [5] | DEBNATH N, DUTTA A, DEB S K. Placement of sensors in operational modal analysis for truss bridges[J]. Mechanical systems and signal processing, 2012, 31: 196-216. DOI:10.1016/j.ymssp.2012.04.006. |
| [6] | YI T H, WANG X, LI H N. Optimal placement of triaxial accelerometers using modal kinetic energy method[J]. Applied mechanics and materials, 2012, 166-169: 1583-1586. DOI:10.4028/www.scientific.net/AMM.166-169. |
| [7] |
伊廷华, 李宏男, 顾明. 基于模型缩聚的广州新电视塔传感器优化布置研究[J].
工程力学, 2012, 29 (3): 55-61.
YI Tinghua, LI Hongnan, GU Ming. Research on optimal sensor placement of Guangzhou new TV tower based on model reduction[J]. Engineering mechanics, 2012, 29(3): 55-61. |
| [8] | UDWADIA F E. Methodology for optimum sensor locations for parameter identification in dynamic systems[J]. Journal of engineering mechanics, 1994, 120(2): 368-390. DOI:10.1061/(ASCE)0733-9399(1994)120:2(368). |
| [9] |
李东升, 张莹, 任亮, 等. 结构健康监测中的传感器布置方法及评价准则[J].
力学进展, 2011, 41 (1): 39-50.
LI Dongsheng, ZHANG Ying, REN Liang, et al. Sensor deployment for structural health monitoring and their evaluation[J]. Advances in mechanics, 2011, 41(1): 39-50. |
| [10] | KAMMER D C. Sensor placement for on-orbit modal identification and correlation of large space structures[J]. Journal of guidance, control, and dynamics, 1991, 14(2): 251-259. DOI:10.2514/3.20635. |
| [11] | KAMMER D C, TINKER M L. Optimal placement of triaxial accelerometers for modal vibration tests[J]. Mechanical systems and signal processing, 2004, 18(1): 29-41. DOI:10.1016/S0888-3270(03)00017-7. |
| [12] | YI Tinghua, LI Hongnan, WANG Chuanwei. Multiaxial sensor placement optimization in structural health monitoring using distributed wolf algorithm[J]. Structural control & health monitoring, 2016, 23(4): 719-734. |
| [13] | CASTRO-TRIGUERO R, SAAVEDRA FLORES E I, DIAZDELAO F A, et al. Optimal sensor placement in timber structures by means of a multi-scale approach with material uncertainty[J]. Structural control & health monitoring, 2014, 21(12): 1437-1452. |
| [14] | NIMITYONGSKUL S, KAMMER D C. Frequency response based sensor placement for the mid-frequency range[J]. Mechanical systems and signal processing, 2009, 23(4): 1169-1179. DOI:10.1016/j.ymssp.2008.11.006. |
| [15] | FRISWELL M I, CASTRO-TRIGUERO R. Clustering of sensor locations using the effective independence method[J]. AIAA journal, 2015, 53(5): 1388-1391. DOI:10.2514/1.J053503. |
| [16] | LI Shiqi, ZHANG Heng, LIU Shiping, et al. Optimal sensor placement using FRFs-based clustering method[J]. Journal of sound and vibration, 2016, 385: 69-80. DOI:10.1016/j.jsv.2016.09.004. |
| [17] | 李宾宾. 基于信息论的结构健康监测传感器优化布置[D]. 大连: 大连理工大学, 2012. LI Binbin. Information theoretic optimal sensor placement in structural health monitoring[D]. Dalian: Dalian University of Technology, 2012. |
| [18] |
周述美, 鲍跃全, 李惠. 基于子结构灵敏度分析的传感器优化布置[J].
地震工程与工程振动, 2014, 34 (4): 242-247.
ZHOU Shumei, BAO Yuequan, LI Hui. Optimal sensor placement based on substructure sensitivity analysis[J]. Earthquake engineering and engineering dynamic, 2014, 34(4): 242-247. |
| [19] | 白雪. 聚类分析中的相似性度量及其应用研究[D]. 北京: 北京交通大学, 2012. BAI Xue. Similarity measures in cluster analysis and its applications[D]. Beijing: Beijing Jiaotong University, 2012. |
| [20] |
何龙军, 练继建, 马斌, 等. 基于距离系数-有效独立法的大型空间结构传感器优化布置[J].
振动与冲击, 2013, 32 (16): 13-18.
HE Longjun, LIAN Jijian, MA Bin, et al. Optimal sensor placement for large space structures based on distance coefficient-effective independence method[J]. Journal of vibration and shock, 2013, 32(16): 13-18. |



