近年来,基于事件驱动的方法在多智能体研究中得到广泛关注[1-3]。在事件驱动的思想中,智能体可以根据测量误差间歇性的更新状态,减少通信次数和计算量。文献[4]首次在多智能体系统的协作中运用事件驱动的策略,并设计了基于事件驱动机制的状态反馈控制器。随后,文献[5-7]将基于事件驱动的控制器扩展到非线性系统,以及复杂网络等领域。但是,目前事件驱动与强化学习的结合还相对不足[8-9],并主要集中在对多智能体的控制器设计上,较少有学者关注其在学习策略层的应用。在现有的多智能体强化学习算法中,由于智能体携带的通信设备和微处理器性能有限,其学习过程中通常存在两个问题:1) 智能体间的信息交互需占用较大的通信带宽;2) 在学习的试错和迭代过程中,消耗了大量的计算资源。以上问题都将减少智能体的工作时间,或增加设计上的复杂性。本文区别于传统的多智能体学习算法,侧重于事件驱动在多智能体学习策略层的研究,首先从自触发和联合触发两个方面定义触发函数,然后在分布式马尔可夫模型中设计了基于事件驱动的多智能体强化学习算法,最后对算法的收敛性进行了论证。
1 问题描述 1.1 分布式马尔可夫模型考虑一个分布式马尔可夫模型 (decentralized markov decision processes, DEC-MDPs),是由一个五元组〈I, {S}, {Ai}, P, R〉构成的,其中,I表示有限的智能体集合;{S}表示一个有限的系统状态集合;{Ai}表示智能体i可采取的动作的集合;P表示系统的转移;R表示回报函数。DEC-MDPs与多智能体的马尔可夫模型 (multi agent-MDPs, M-MDPs) 的唯一区别在于,在M-MDPs中系统的全局信息被所有智能体完全获得,而在DEC-MDPs中,每一个智能体仅具有局部的观测,或者说是全局信息的一个子集,当所有的子集放在一起求并集时,这些局部信息能够合成一个完整的全局信息,在完全通信的情况下,DEC-MDPs可以被简化为M-MDPs模型。求解DEC-MDPs的目的是找到一个联合策略
文献[11]提出了一类通过引入期望的延时回报,求解无完全信息的MDPs类问题的方法,称为Q-学习 (Q-learning)。Q-学习是一种模型无关的强化学习方法,通过对状态-动作对的值函数进行估计,以求得最优策略。Q-学习算法的基本形式如下:
 |
式中:Q*(s, a) 表示智能体在状态s下采用动作a所获得的奖赏折扣总和;γ为折扣因子;P(s, a, s′) 表示概率函数;最优策略为智能体在状态s下选用Q值最大的策略。Q-学习存在的最大问题为,智能体需要通过试错的方式找到最优策略,这样的方式使得Q-学习需要考虑所有的可能策略,从而需要消耗大量计算资源。
2 触发规则设计在事件驱动思想中,智能体把从环境中得到的观测误差作为重要的评判标准,当它超过一个预设的阈值时事件被触发,智能体更新状态并计算联合策略,而事件触发的关键在于对触发函数的设计。
2.1 自事件触发设计DEC-MDPs模型中,每一个智能体通过独立的观测获取局部信息,然后广播到全队,所以每一个智能体首先需要自触发设计。在时刻t,当每一个智能体观测结束后,其根据上一刻观测与当前观测的变化率,进行一次自触发过程,智能体用自触发方式来判断是否需要广播自身的观测信息。智能体i从t-1时刻到t时刻的观测变化率定义为
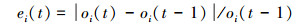 |
(1) |
式中:oi(t) 为在t时刻的观测值。定义0 < e < 1为自事件触发函数阈值,当智能体i观测信息的变化率ei(t) 大于e时进行通信。此时,不一定所有的智能体都被驱动,没有采集到新观测信息的智能体仅接收信息。在自事件触发过程,智能体无需每一时刻进行通信,因此减少智能体的通信消耗。
2.2 联合事件触发设计联合事件触发的对象是智能体团队,考虑的是一个联合观测的变化情况。假设在时刻t智能体团队获得当前的联合观测O (t)=(O1(t), O2(t), …, On(t))。此时,智能体团队从t-1时刻到t时刻的联合观测变化率定义为
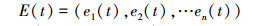 |
(2) |
式中:ei(t)=oi(t)-oi(t-1)/oi(t-1)。
利用方差计算两个时刻的误差偏移程度,令联合观测变化率期望为
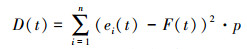 |
(3) |
式中:p=1/n为ei(t) 的分布律,令
 |
(4) |
定义0 < G < 1为团队的联合事件触发函数阈值,当H(t) 大于G时,认为智能体团队的状态已经发生较大改变,需要对Q值表进行遍历,并计算一个新的联合策略,否则智能体直接延用上一刻的联合策略。
自事件触发和联合事件触发的区别在于:
1) 自事件触发的对象是单个智能体,对应的事件由智能体自身的观测变化率所触发,触发后的行动为进行广播式通信,自事件触发的目的是为了减少通信资源消耗;而联合事件触发针对的是智能体团队的联合观测变化率,触发后的行动是计算联合策略,目的在于减少计算资源消耗。
2) 当单个智能体的观测发生变化时,并不一定导致团队的联合观测变化率发生较大改变。即当环境整体发生变化时,虽然每一个智能体的观测都发生了变化,但对联合观测而言,所有智能体在两个时刻的变化率相对无变化,所以制定的联合策略可能无明显变化,此时也认为智能体团队不需要被触发。比如在机器人足球问题中,t-1时刻机器人团队的联合策略为,机器人A带球行动且其他队友跑位行动。到t时刻后,机器人A和其他机器人的观测 (双方机器人的站位和距离) 都发生了较大变化,机器人团队在通过广播通信获得全局观测信息后,根据观测信息进行判断,两个时刻双方机器人的相对站位和相对距离可能无大变化。此时,如果团队计算新的联合策略,也将是机器人A带球且其他队友跑位,与t-1时刻的联合策略相同。所以,认为团队在t时刻无需计算新的联合策略,可以直接使用上一刻的策略。图 1为事件触发流程图。

|
| 图 1 事件触发流程图 Fig. 1 The flow chart of event-triggered |
本节介绍了基于事件驱动的强化学习算法,以及对事件驱动下计算资源消耗进行了分析,同时对算法的收敛性进行了论证。
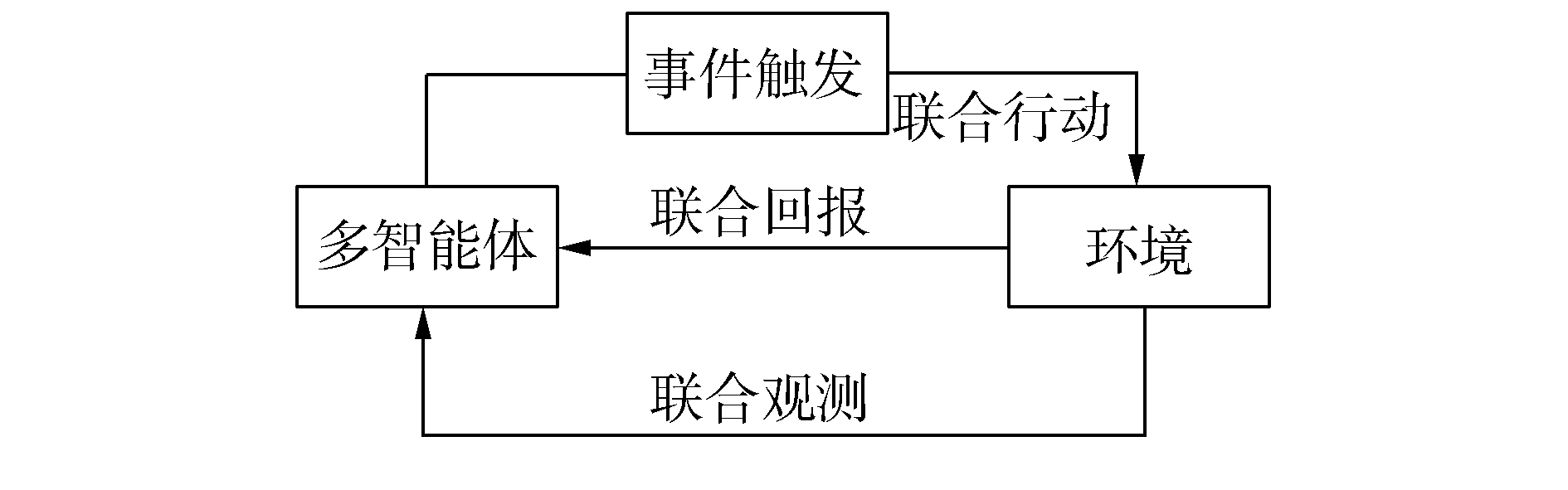
3.1 基于事件驱动的强化学习设计在完全通信情况下,DEC-MDPs被简化为M-MDPs模型, 所以直接考虑基于事件驱动的多智能体马尔可夫模型 (event-triggered M-MDPs),其由一个六元组〈I, {S}, {Ai}, P, R, e〉构成,其中e表示事件触发函数,当团队的触发函数大于阈值时,团队被触发并执行联合行动策略,同时发生状态转移,转移函数为P={st+1|st, a, e}。基于事件驱动的强化学习过程不同于经典的强化学习,如图 2所示,智能体需要首先根据触发函数来判断事件是否被触发,如果被触发才执行一个联合行动并影响环境。
|
| 图 2 基于事件驱动的强化学习框架 Fig. 2 The frame of reinforcement learning with event-triggered |
强化学习的目的是找到一个策略使团队获得最大的奖励信号。如果在所有状态下,策略π的期望回报值都大于或等于策略π′的,那么称之为最优策略。最优策略可能有多个,都将其称作最优策略,记π*,而最优策略对应的状态-联合动作对 (s, 
基于事件驱动的Q-学习算法,类似于经典Q-学习,均是不去估计环境模型,而是直接优化一个可迭代计算的Q函数。区别在于,经典Q-学习中,智能体在每一个时刻都需要对Q值进行迭代计算,而基于事件驱动的Q-学习,仅在智能体被触发的情况下,Q值才进行迭代计算。此时,定义Q函数为在状态st时被触发并执行联合动作
 |
(5) |
对于任意一个策略和下一个状态,在状态s的值和后继状态值之间存在如下关系:
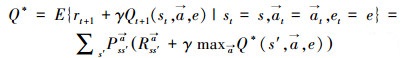 |
(6) |
式 (6) 为贝尔曼公式,它表示了当前状态和其后继状态之间的联系。图 3表示了强化学习中Q值迭代与状态转移的回溯关系。图 3(a)中,每一个实心点表示一个状态-联合动作对,每一个空心点表示一个状态,智能体从一个状态-联合动作对出发,依次到达下一个状态。在图 3(b)中,智能体团队在st+1状态下得到最优策略 (st +1, 


|
| 图 3 两种方式回溯图 Fig. 3 The backtracking of two methods |
根据贝尔曼迭代,Q值逐渐收敛到一个最优Q值,在传统的强化学习中,每一个学习步智能体都需要通过查表方式找到最大的Q值,其迭代表达式为
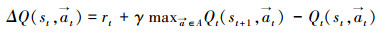 |
(7) |
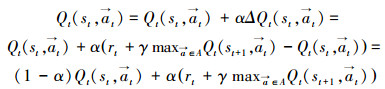 |
(8) |
事件驱动的思路则不同,当智能体没有被触发情况下,将直接选用上一个Q值作为当前的Q值,在基于事件驱动的Q-学习中,Q值迭代过程可以表示为
 |
(9) |
式中k表示上次触发时刻和当前时刻的差值。
3.2 计算资源消耗Q-学习中的计算资源消耗,主要体现在智能体需要对所有策略进行试错。从决策树角度看,树根和树枝对应着智能体团队的状态与观测,其在每一次观测后,根据不同的观测都会转移到不同的下一刻状态,即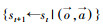


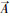
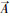
对于基于事件驱动的决策树,在智能体不被驱动的树层中,下一刻状态将直接等于当前状态,即st+1=st,状态转移概率为
 |
状态转移概率Pr=1意味着,此时整棵决策树中不被驱动的树层不生成树枝,进而也减少下一层中树枝对应的树根。同理,不生成新的树枝,智能体也无需对当前树层里所有的Q值进行遍历。上述例子中,假设t步中存在k次不被驱动,那么在t步学习过程中, 遍历Q值的次数为 (ni×m i)×(t-k) 次。
3.3 算法收敛性分析智能体每次的策略评估,即策略迭代,都是从前一个策略的值函数开始。在事件驱动的强化学习中,智能体只有在观测信息变化情况下,才更新信念空间并进行策略评估,否则直接使用上一时刻的策略。假设在t时刻,智能体没有被事件所触发,那么智能体在t时刻不参与式 (9) 的迭代,直接使用t-1时刻迭代后的Q值。此时,在达到最优策略的过程中,Q值的迭代计算过程由每一时刻都计算,减少为事件触发时刻才计算。
 |
(10) |
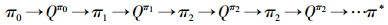 |
(11) |
如图 4(a)和式 (10) 所示,Q值从初始到收敛至最优Q*的过程,是一个渐进收敛的过程,Q值通过迭代,从t-1时间到t时刻逐渐接近最优;如图 4(b)和式 (11) 所示,在智能体不被驱动的情况下,Q值不进行迭代,在t-1时刻直接使用t时刻的Q值,减少了Q值的迭代计算。

|
| 图 4 两种方式策略迭代 Fig. 4 Policy iteration of two methods |
推论1 基于事件驱动的Q-学习算法,不会影响算法的收敛性。
引理1 收敛引理[12]。令χ为一个任意的集合,假设B是χ中一个空间有界的集合,即B(χ), T:B(χ)→B(χ)。v*为T的一个固定点,令τ=(T0, T1, …) 为来自F0(v*) 的初值,τ在v*点逼近T,假设F0为τ中一个不变式。令V0∈F0(v*),定义Vt+1=Tt(Vt, Vt)。如果存在随机函数0≤Ft(x)≤1和0≤Gt(x)≤1以概率1满足以下条件,那么在B(χ) 中Vt以概率1收敛到v*:
1) 对所有的U1和U2∈F0, 对所有的x∈χ,
 |
(12) |
2) 对所有的U和V∈F0, 对所有的x∈χ,
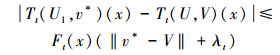 |
(13) |
式中:当t→∞时,λt以概率1收敛到0。
3) 对所有的k>0, 当t→∞时,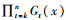
4) 当t→∞时,存在0≤γ < 1对所有的x∈X有
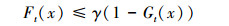 |
(14) |
证明 在事件驱动的强化学习中,令T=(T0, T1, …, Tk, Tk+1=Tk, Tt, …) 为一个动作序列,表示智能体执行行动后从当前状态到下一个状态的映射,其中 (…Tk, Tk+1…) 指当智能体在没有被事件驱动的情况下智能体的第Tk+1个行动等于第Tk个行动,同时,迭代过程为
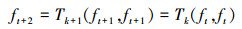 |
(15) |
令V, U0, V0∈B(χ),Ut+1=Tt(Ut, V),Vt+1=Tt(Vt, v*),δt(x)=|Ut(x)-Vt(x)|。根据收敛引理有
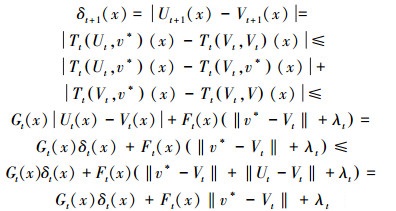 |
(16) |
在满足条件1) 和2) 的情况下,虽然基于事件驱动的动作序列T中有相同的动作Tk=Tk+1,但仍然满足李普西斯条件,所以不会影响Q-学习的收敛,证毕。
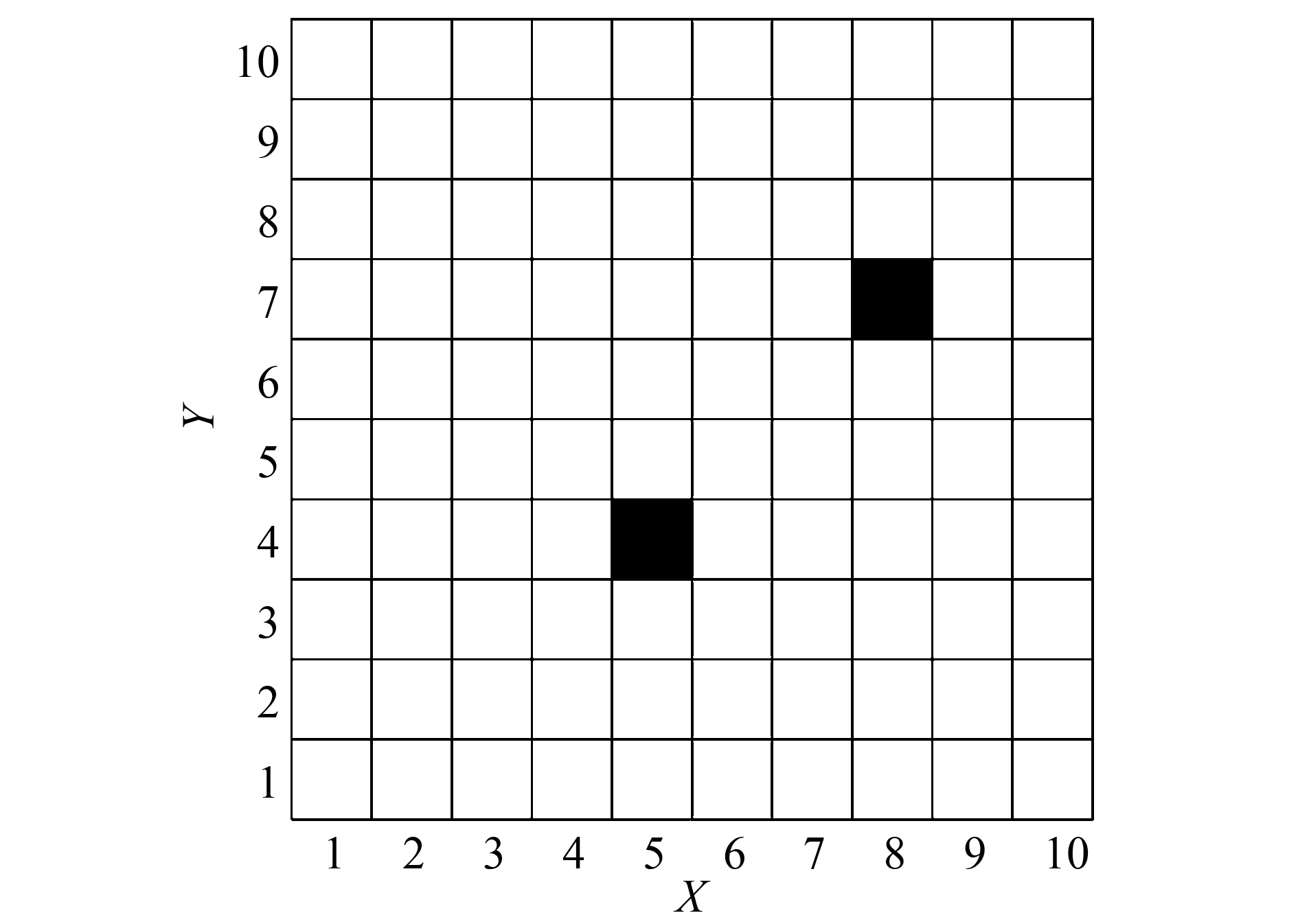
4 仿真结果及分析考虑一个多智能体覆盖问题,2个智能体随机出现在一个大小为10×10的格子世界中,如图 5所示。每一个智能体都有上下左右4个行动,且观测范围为自身周围一圈共8个格子,观测到的格子分为“没走过”“走过”和“障碍物”3个状态,分别对应着30、-5和-10的回报值,世界的边界对智能体作为障碍物;且每一个智能体可以进行广播式通信。在这个场景中,每一个智能体获得的是一个局部观测,当它们进行广播通信后,对于整个世界,获得的仍然是一个局部的观测。但考虑到对整个世界的全局观测需要极大的计算量,所以实验设定每一时刻当两个智能体通信后,所获得的信息对它们而言是一个全局观测。
|
| 图 5 多智能体覆盖问题 Fig. 5 The coverage problem of multi-agent |
智能体团队的任务为尽快走完所有的格子,即完成对格子世界的覆盖,当走过的格子超过90%以上,认为此次覆盖任务成功,当智能体在1 000步仍不能完成90%的覆盖时,认为此次任务失败。其中定义学习率为0.6,折扣因子为0.2。
图 6比较了事件驱动与传统Q-学习任务成功率,可以看出两种算法成功率一致,但是由于Q值迭代次数减少,使得事件驱动Q-学习的收敛速度变慢。

|
| 图 6 事件驱动与传统Q-学习的成功率 Fig. 6 The success rate of event-triggered Q and classical Q |
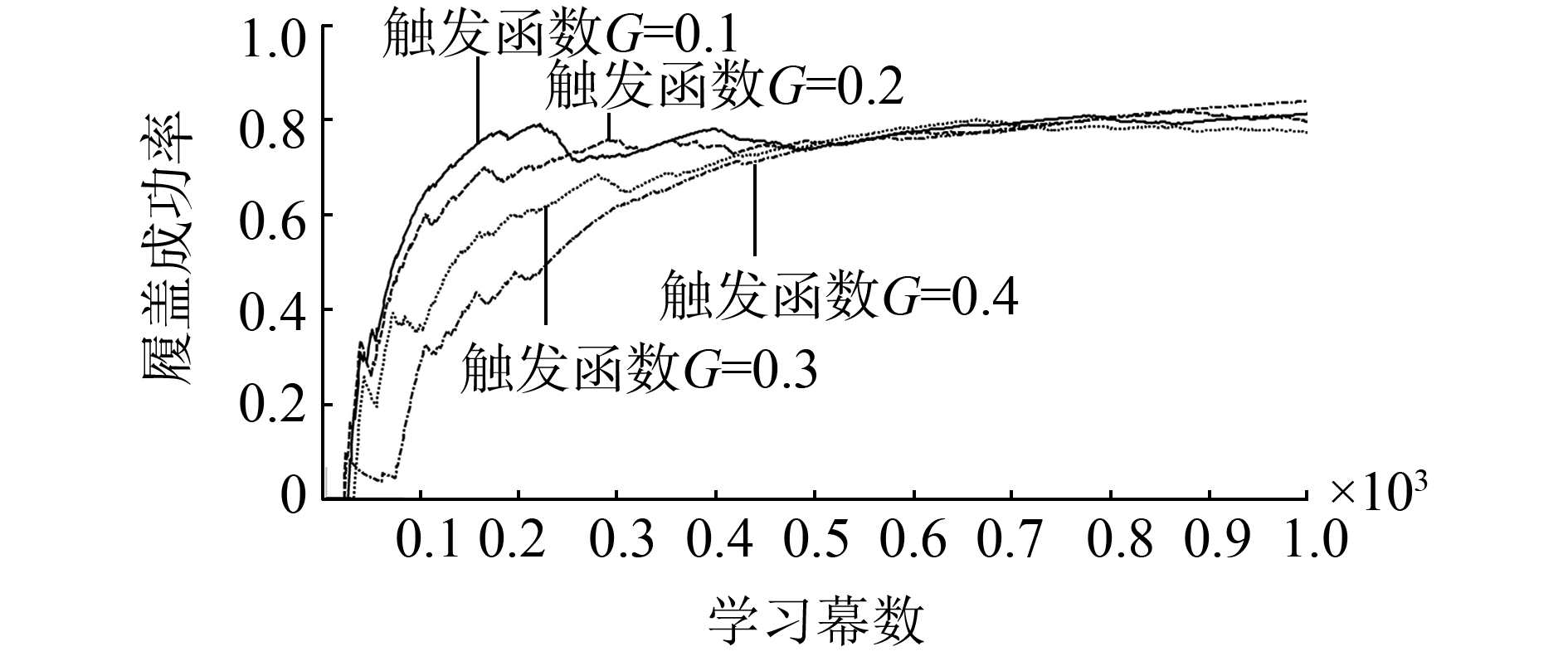
图 7说明了联合触发函数与算法收敛速度的关系,可以看出联合触发函数选取越小,算法收敛性越慢。因为联合触发函数越小,事件触发的次数就越少,从而导致Q值迭代次数减少,收敛速度变慢。
|
| 图 7 联合触发函数与收敛速度 Fig. 7 The joint event-triggered function and convergence speed |
在学习过程中,智能体团队在每一步需要遍历Q值数量为 (38×4)2≈229.3次,由表 1可以看出,随着学习步数的增加,事件驱动将大量减小Q值的遍历次数,继而减少计算资源占用,相比较传统的Q-学习存在明显的优势。
| 步数 | Q-学习 | 事件驱动Q-学习 | 减少总遍历次数 |
| 50 | ≈229.3×50 | ≈229.3×42 | ≈232.3 |
| 100 | ≈229.3×100 | ≈229.3×79 | ≈233.6 |
| 200 | ≈229.3×200 | ≈229.3×153 | ≈234.9 |
| 300 | ≈229.3×300 | ≈229.3×221 | ≈235.6 |
| 500 | ≈229.3×500 | ≈229.3×386 | ≈236.2 |
表 2比较了在一次成功的任务中,事件驱动与传统Q-学习的通信次数。可以看出,事件驱动减少了智能体间的通信次数。同时与表 1比较,可以看出自事件触发和联合事件触发次数的区别。
| 步数 | Q-学习 | 事件驱动Q-学习 | 减少通信次数 |
| 50 | 50 | 45 | 5 |
| 100 | 100 | 89 | 11 |
| 200 | 200 | 172 | 28 |
| 300 | 300 | 258 | 42 |
| 500 | 500 | 410 | 90 |
5 结束语
本文提出了一种基于事件驱动的多智能体强化学习算法,侧重于多智能体在学习策略层的事件驱动研究。智能体在与环境的交互中,可以根据观测的变化来触发通信和学习过程。在相同时间内,采用事件驱动可以降低数据传输次数,节约通信资源;同时,智能体不需要每一时刻进行试错和迭代,进而减少计算资源。最后,对算法的收敛性进行了论证,仿真结果表明事件驱动可以在学习过程中减少一定的通信次数和策略遍历次数,进而缓解通信和计算资源消耗。进一步工作主要基于现有的研究, 将事件驱动的思想应用于不同类的强化学习方法中,并结合事件驱动的特点设计更合理的触发函数。
| [1] | ZHU Wei, JIANG ZhongPing, FENG Gang. Event-based consensus of multi-agent systems with general linear models[J]. Automatica, 2014, 50(2): 552-558. DOI:10.1016/j.automatica.2013.11.023. |
| [2] | FAN Yuan, FENG Gang, WANG Yong, et al. Distributed event-triggered control of multi-agent systems with combinational measurements[J]. Automatica, 2013, 49(2): 671-675. DOI:10.1016/j.automatica.2012.11.010. |
| [3] | WANG Xiaofeng, LEMMON M D. Event-triggering in distributed networked control systems[J]. IEEE transactions on automatic control, 2011, 56(3): 586-601. DOI:10.1109/TAC.2010.2057951. |
| [4] | TABUADA P. Event-triggered real-time scheduling of stabilizing control tasks[J]. IEEE transactions on automatic control, 2007, 52(9): 1680-1685. DOI:10.1109/TAC.2007.904277. |
| [5] | ZOU Lei, WANG Zidong, GAO Huijun, et al. Event-triggered state estimation for complex networks with mixed time delays via sampled data information: the continuous-time case[J]. IEEE transactions on cybernetics, 2015, 45(12): 2804-2815. DOI:10.1109/TCYB.2014.2386781. |
| [6] | SAHOO A, XU Hao, JAGANNATHAN S. Adaptive neural network-based event-triggered control of single-input single-output nonlinear discrete-time systems[J]. IEEE transactions on neural networks and learning systems, 2016, 27(1): 151-164. DOI:10.1109/TNNLS.2015.2472290. |
| [7] | HU Wenfeng, LIU Lu, FENG Gang. Consensus of linear multi-agent systems by distributed event-triggered strategy[J]. IEEE transactions on cybernetics, 2016, 46(1): 148-157. DOI:10.1109/TCYB.2015.2398892. |
| [8] | ZHONG Xiangnan, NI Zhen, HE Haibo, et al. Event-triggered reinforcement learning approach for unknown nonlinear continuous-time system[C]//Proceedings of 2014 International Joint Conference on Neural Networks. Beijing, China, 2014: 3677-3684. |
| [9] | XU Hao, JAGANNATHAN S. Near optimal event-triggered control of nonlinear continuous-time systems using input and output data[C]//Proceedings of the 11th World Congress on Intelligent Control and Automation. Shenyang, China, 2014: 1799-1804. |
| [10] | BERNSTEIN D S, GIVAN R, IMMERMAN N, et al. The complexity of decentralized control of Markov decision processes[J]. Mathematics of operations research, 2002, 27(4): 819-840. DOI:10.1287/moor.27.4.819.297. |
| [11] | WATKINS C J C H, DAYAN P. Q-learning[J]. Machine learning, 1992, 8(3/4): 279-292. DOI:10.1023/A:1022676722315. |
| [12] | SZEPESVÁRI C, LITTMAN M L. A unified analysis of value-function-based reinforcement-learning algorithms[J]. Neural computation, 1999, 11(8): 2017-2060. DOI:10.1162/089976699300016070. |



