2. 山西大学 计算智能与中文信息处理教育部重点实验室, 山西 太原 030006
2. Key Laboratory of Computation Intelligence and Chinese Information Processing, Ministry of Education, Shanxi University, Taiyuan 030006, China
近年来,对各种复杂网络的研究是许多领域的研究热点之一[1,2,3],如生物网络、社交网络、电子邮件网络、引文网络等已成为众多学者的主要研究对象。大量研究表明,复杂网络中存在着一种普遍特征——社区结构[4]。复杂网络中社区发现[5]不仅有助于深入研究整个网络的拓扑结构、功能模块以及动力学特性,同时在生物蛋白质的性能与互作用的分析[6]、社会组织结构的网络分析[7]、搜索引擎[8]及推荐系统[9]等方面均有广泛的应用前景,因此具有十分重要的理论意义和应用价值。
目前,社区发现算法的研究主要分为基于图划分的聚类算法[10, 11]、基于谱分析的聚类算法[12]、基于层次的聚类算法[13]和基于密度的聚类算法[14]等。其中基于密度的聚类算法通过搜索网络中稠密子图[15]能较好地发现网络中的功能模块,因此在社区发现中得到了广泛应用。2005年,Palla等[16]提出派系过滤算法(clique percolation method,CPM),首先挖掘网络中结点数大于k的所有派系(完全图),然后将重叠结点大于k-1的派系合并得到k派系社区。2006年,Saito等[17]提出k-dense子图结构,通过寻找网络中的k-dense结构进行社区检测。2009年,Sun等[18]以CPM为基础,通过改进寻找派系的方法提高算法效率,提出迭代派系过滤算法(iterative-clique percolation method,ICPM)。2010年,Liu等[19]提出基于极大团的聚类算法(clustering-based on maximal cliques,CMC),通过搜索网络中的所有极大团,并依据相互连接度合并重叠率较高的极大团得到网络的社区结构。由于这些算法要搜索网络中的相对稠密子图来进行聚类,当网络中存在包含大量结点的稀疏子图时,这些结点可能最终成为未聚类结点,造成了聚类结果的不完全覆盖。这些未聚类结点构成的稀疏子图可能具有某种功能,或者与某些稠密子图共同行使功能,因此需要对网络中的部分未聚类结点进行进一步分析,判断其是否属于某一社区或形成新的社区。
针对基于密度算法中大量未聚类结点问题,提出一种基于稠密子图的社区发现算法(community detection based on dense subgraphs,BDSG)。首先通过搜索网络中的相对稠密子图得到中心社区;对于未聚类结点,定义了结点 v对社区C的归属度b(v,C)来度量结点和社区的连接倾向程度;基于归属度,给出一种中心社区扩展策略 (core community extended strategy,CE),对未聚类结点进一步处理。BDSG算法中,一个结点可能属于多个社区,是一种软聚类方法。通过在空手道俱乐部、海豚社交网络、大学生足球网络、电子邮件网络和合作网络 5个真实网络上与CPM、k-dense算法进行比较,评估和分析BDSG算法在未聚类结点分配和社区模块性等方面的性能表现。基于归属度的中心社区扩展策略也将应用在CPM、k-dense等基于密度的图聚类算法中,对未聚类结点进一步处理,以提高聚类有效性。
1 背景知识通常,一个复杂网络可以表示为图G=V,E,其中顶点集V=v1,v2,…,vn,n=V;边集E中每条边ei,j对应V中一对顶点(vi,vj)之间的连接关系,m=|E|。顶点v的邻域NGv=u|v,u∈E,表示图G中与顶点v相邻的顶点集合,简记为Nv。结点v的度记为kv。除非特别指明,以下仅考虑简单无向图,因此kv=|Nv|。令UVG,用UG表示G的结点子集U的导出子图,在不发生混淆时,记为U。记顶点子集U在G中的邻域为NG(U)={u|u∈NGx∧x∈U}。
在复杂网络中,图G的密度[20]记为 ${{D}_{G}}\in \frac{m}{n(n-1)/2}$。可以看出,DG∈0,1,当DG越趋近于1,图G中的边数越多;当DG=1时,图G为完全图。
结点vk的点介数[21]Bvk可以用来度量结点vk在网络G中的重要性。如果一对结点(vi,vj)间共有Lvi,vj条不同的最短路径,其中有Lvi,vjvk条经过结点vk,那么结点vk对结点对(vi,vj)的贡献为Lvi,vjvk/Lvi,vj。定义结点vk的点介数Bvk:
| \[B\left( {{v}_{k}} \right)=\sum\limits_{i=1}^{n}{\sum\limits_{j=i+1}^{n}{\frac{{{L}_{vi,vj}}\left( vk \right)}{{{L}_{vi,vj}}}}}\] | (1) |
通常一个结点的点介数越大,则该结点对网络结构的影响越大。点介数是网络中结点重要性度量指标之一。
2 结点对社区的归属度定义基于密度的图聚类算法中可能存在大量不属于任何已有社区的未聚类结点,为了将这些结点聚类到合适的社区,需要定义未聚类结点和社区的关联强度,称为结点 v对于社区C的 归属度b(v,C)。归属度的定义对聚类结果的影响至关重要,结点v对于社区C的归属度越大,则结点v属于社区C的可能性越大。
Cui等[22]基于结点v与社区C关联边数定义了结点v对于社区C的归属度${{b}_{p}}\left( v,C \right)=\frac{\left| {{N}_{v}}\cap c \right|}{{{k}_{v}}}$,其中Nv∩C=u|v,u∈E,u∈C表示结点v在社区C中相邻点的集合,kv是结点v的度。然而结点v与社区C的关联强度不仅与关联边数有关,也和社区C中v的相邻点在C中的重要性关系密切。
如图 1所示,当前聚类结果得到两个社区C1(▲)和C2(■),其余结点为未聚类结点。考虑结点v9,可得bp(v9,C1)=bp(v9,C2),Nv9∩C1=v33,v34,且Nv9∩C2=v1,v3。此时,社区C1中与结点v9相邻结点的点介数比例为$\frac{\sum\nolimits_{u\in \left\{ {{v}_{33}},{{v}_{34}} \right\}}{B\left( u \right)}}{\sum\nolimits_{w\in {{c}_{1}}}{B\left( w \right)}}=0.95$,而社区C2中与结点v9相邻结点的点介数比例为$\frac{\sum\nolimits_{u\in \left\{ {{v}_{1}},{{v}_{3}} \right\}}{B\left( u \right)}}{\sum\nolimits_{w\in {{c}_{2}}}{B\left( w \right)}}=0.83$。由于结点v9在C1中的相邻点在网络中重要性更高,可以认为v9更倾向归属于社区C1。
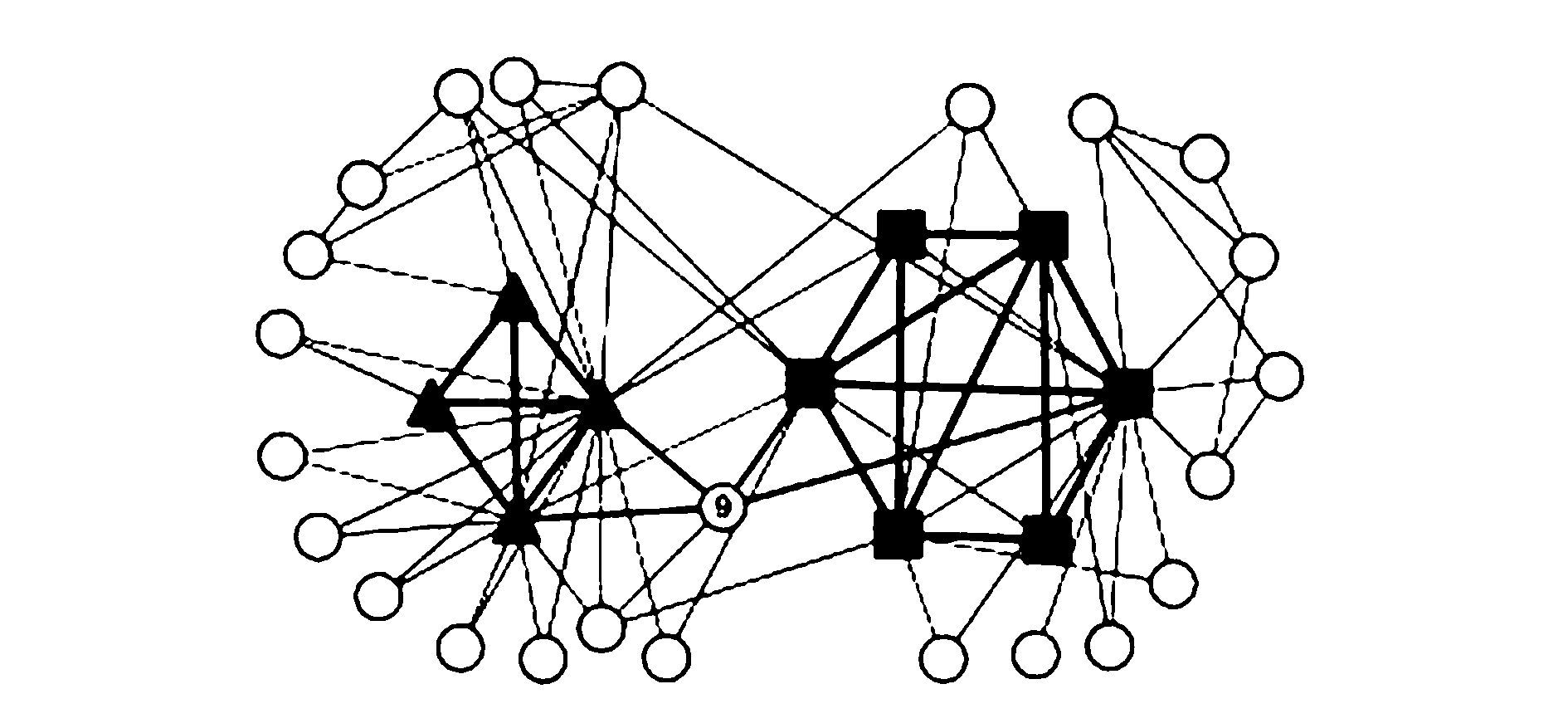
|
| 图 1 空手道俱乐部中未聚类结点分析 Fig. 1 The analysis of subordinate vertices in zacharys karate club |
因此,度量未聚类结点和已有社区的归属度,需要综合考虑该结点与一个社区关联边数以及社区内该结点的相邻结点的重要性。为了更准确地表示未聚类结点和社区的关系,首先给出结点v对社区C的归属度定义:
\[b\left( v,c \right)=\alpha \times \frac{\left| {{N}_{v}}\cap C \right|}{{{k}_{v}}}+\left( 1-\alpha \right)\times \frac{\sum\nolimits_{ui\in {{N}_{v}}\bigcap c}{B\left( {{v}_{j}} \right)}}{\sum\nolimits_{vj\in c}{B\left( {{v}_{j}} \right)}}\]
(2)
| 数据集 | 未聚类节点 | Q | ||
| α=0.8 | α=1 | α=0.8 | α=1 | |
| 空手道 俱乐部 | 1 | 3 | 0.820 5 | 0.717 9 |
| 海豚 社交网络 | 0 | 1 | 0.773 5 | 0.761 0 |
| 大学生
足球网络 | 0 | 0 | 0.639 0 | 0.615 0 |
|
电子
邮件网络 | 34 | 41 | 0.722 4 | 0.715 1 |
| 合作网络 | 657 | 661 | 0.782 8 | 0.647 3 |
基于稠密子图的社区发现算法(BDSG)主要由2部分构成:首先通过搜索网络中大于指定密度阈值d的稠密子图得到网络中心社区,确定聚类个数k,不属于任何一个中心社区的结点为未聚类结点;根据式(2)计算未聚类结点与已有社区的归属度,将一些未聚类结点划分到归属度大于指定阈值的社区中,对当前中心社区进行扩展;更新剩余未聚类结点的归属度,若网络中所有未聚类结点对任意社区的归属度都小于设定阈值,则算法结束。
3.1 确定聚类个数首先,寻找网络中的子图密度大于指定阈值 d的所有稠密子图。图 2给出了d=0.9时,算法得到的4个稠密子图,分别记为U1、U2、U3和U4。
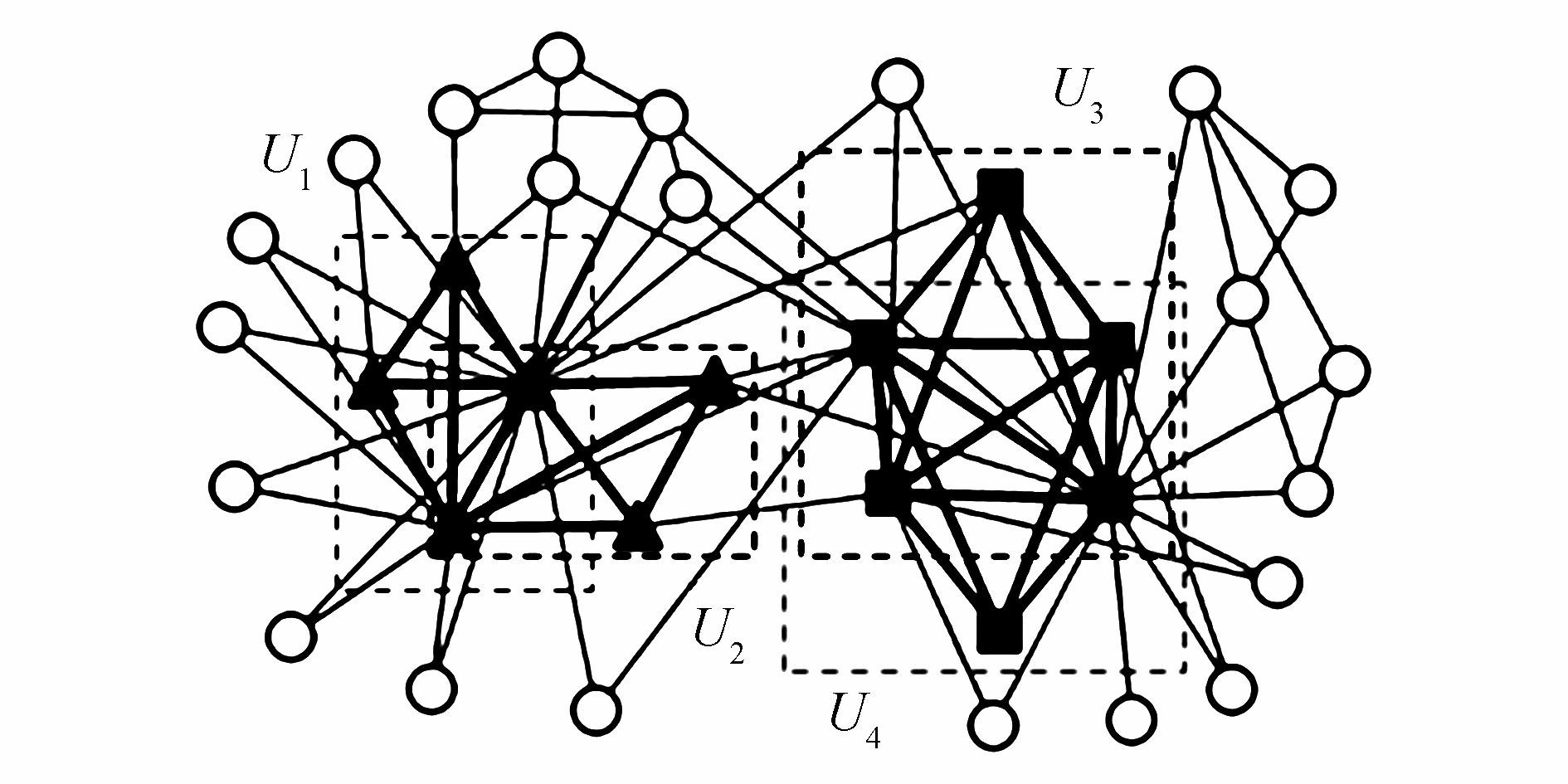
|
| 图 2 BDSG算法在空手道俱乐部中得到的稠密子图 Fig. 2 The dense subgraphs in zacharys karate club obtained by BDSG |
然后,建立子图重叠矩阵
M,其中元素Mi,i=|V(Ui)|表示子图Ui中的顶点个数。元素Mi,i=VUi∩VUj,i≠j,表示子图Ui和Uj的公共顶点数。对2个不同稠密子图,若Mi,i>
$\frac{\min \left( \left| {{U}_{i}} \right|,\left| {{U}_{j}} \right| \right)}{2}
$,则合并2个子图为一个新社区U′=[V(Ui)∪VUj]G,此过程迭代进行,直到不产生新的社区。得到的社区称为初始中心社区,社区个数k为算法的聚类个数。图 2中4个稠密子图的重叠矩阵表示为
\[M=\left\{ \begin{align}
& 4200 \\
& 2400 \\
& 0054 \\
& 0045 \\
\end{align} \right\}\]
算法确定了聚类个数和初始中心社区数之后,不属于任何中心社区的结点就是未聚类结点。由于初始中心社区寻找过程中关注于网络中相对稠密的子图,网络中存在大量未聚类结点,需要设计合理的中心社区扩展策略,对未聚类结点进一步处理。
3.2 中心社区扩展策略设聚类个数为k,当前中心社区分别为C1,C2,…,Ck,则当前未聚类结点集合$T=V\left( G \right)-U_{i=1}^{k}V\left( {{C}_{i}} \right)$。根据式(2)给出的结点对社区的归属度定义,计算T中结点与中心社区Ci的归属度,并对相关中心社区进行扩展,具体过程如算法1。
算法1 中心社区扩展算法 (core community extended strategy,CE)
输入 图G=V,E,聚类个数k,初始中心社区集合C0=C10,C20,…,Ck0,其中Ci0V。
输出 社区集合C=C1,C2,…,Ck。
1)令集合T0=VG-∪i=1kVCi0,β0=0.7,t=0。
2)令t=t+1,对每个社区C>1(t-1),C2(t-1),…,Ck(t-1),执行下列操作:
①Cit=Ci(t-1)(1≤i≤k),NGi(Ct-1)={u|u∈NG(x)∧x∈Ci(t-1)}。
②对任意元素v∈T∩NGCi(t-1)1≤i≤k,如果b(v,C i(t-1))≥βt-1,则Cit=Cit∪v。
③令βt=βt-1-0.1,Tt=VG-∪i=1kVCit,若βt≥0.3,且Tt≠,返回步骤2)。
3) 结束,输出社区集合C=C1t,C2t,…,Ckt。
图 3给出了BDSG算法在空手道俱乐部数据集上的聚类结果,共得到2个社区,空白结点表示未聚类结点。
4 实验与结果分析为了分析研究BDSG算法在真实网络中社区发现的有效性,将BDSG算法分别应用于空手道俱乐部(Karate)[23]、海豚社交网络(Dolphin)[24]、大学生足球网络(Football)[25]、电子邮件网络(Email)[26]和合作网络(NetScience)[27] 等5个数据集。实验所用计算机配置为Inter Core i5 CPU 2.5 GHz,6 GB内存,Windows 7操作系统。程序采用java编程语言并在Eclipse环境下运行。依经验选择密度阈值 d=0.9,调节参数α=0.8。
图 3~5分别给出了本文BDSG算法在空手道俱乐部、海豚社交网络和大学生足球网络的聚类结果。表 2给出了BDSG算法与CPM、k-dense算法分别在聚类个数、未聚类结点数、社区模块性(Q)[28]以及运行时间等方面的比较结果。
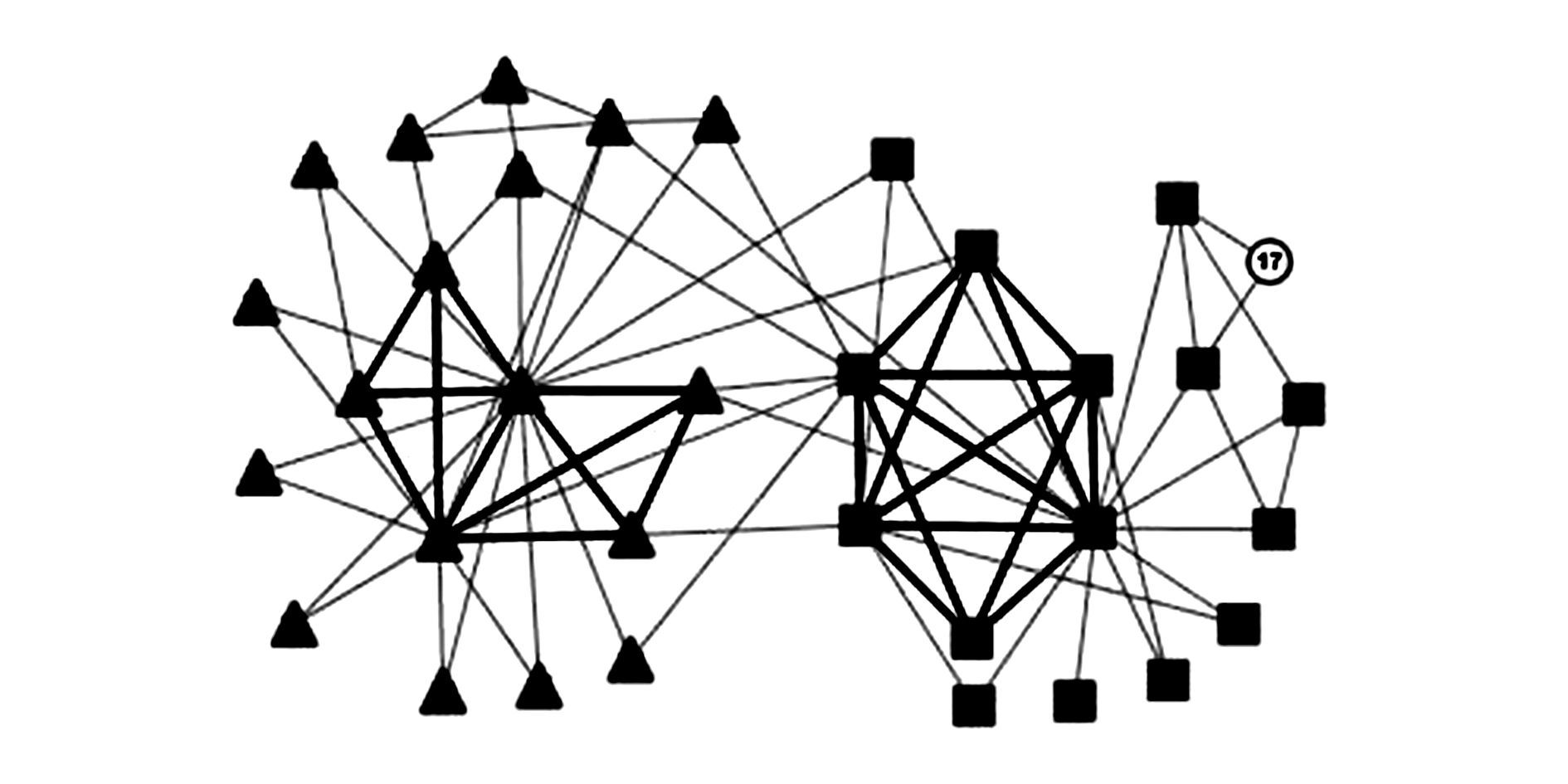
|
| 图 3 BDSG算法在空手道俱乐部得到的聚类结果 Fig. 3 Clustering results on zacharys karate club obtained by BDSG |
|
| 图 4 BDSG算法在海豚社交网络上得到的聚类结果 Fig. 4 Clustering results on dolphins social network obtained by BDSG |
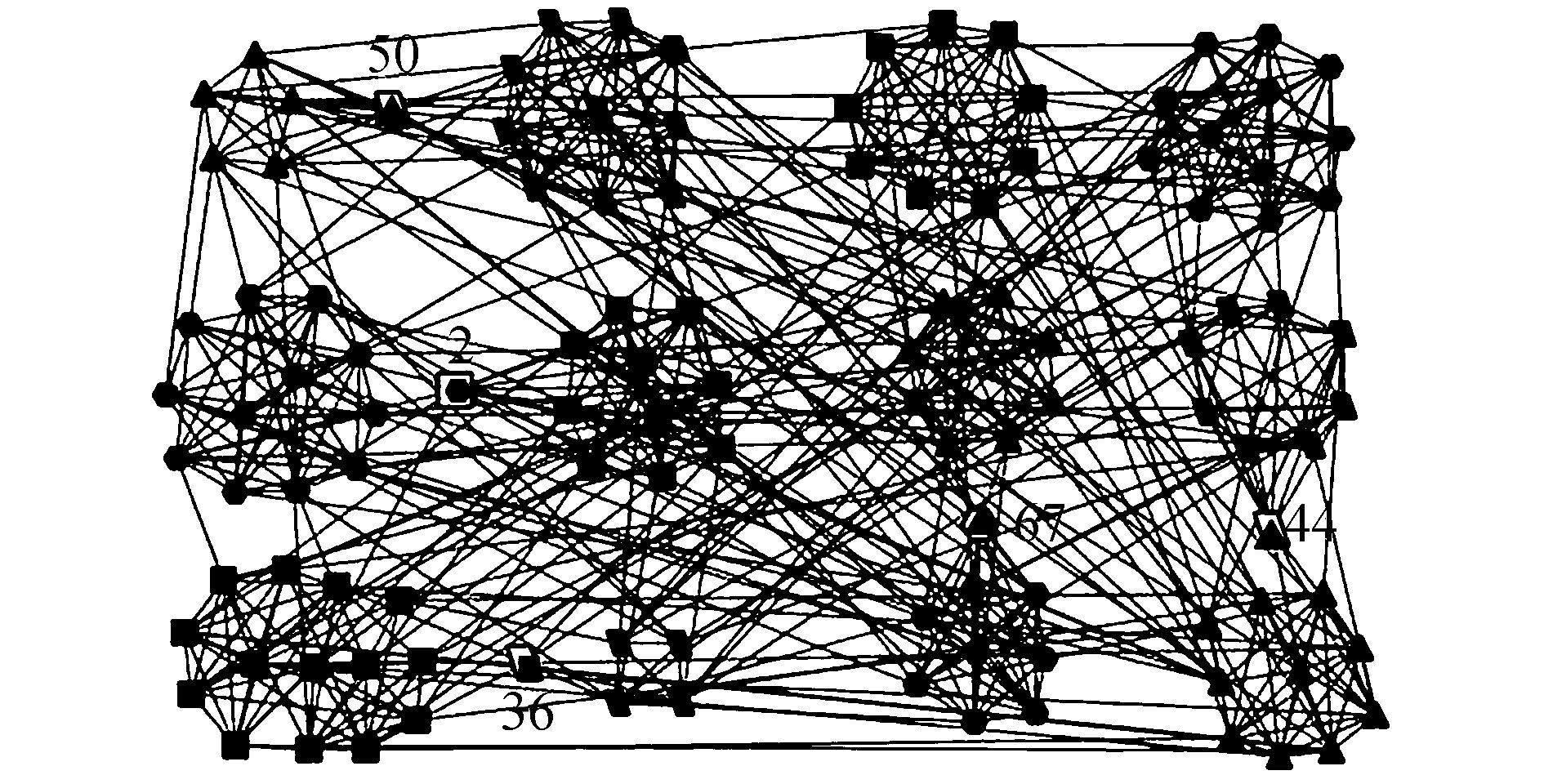
|
| 图 5 BDSG算法在大学生足球网络上得到的聚类结果 Fig. 5 Clustering results on college football network obtained by BDSG |
| 数据集 | 顶点数 | 边数 | 原始社区个数 | 算法 | 聚类个数 | 未聚类节点数 | Q | 运行时间/ms |
| 空手道 俱乐部 | 34 | 78 | 2 | BDSG | 2 | 1 | 0.820 5 | 93 |
| CPM | 3 | 22 | 0.192 3 | 87 | ||||
| k-dense | 2 | 22 | 0.294 8 | 129 | ||||
| CPM+CE | 3 | 3 | 0.410 2 | 117 | ||||
| k-dense+CE | 2 | 1 | 0.820 5 | 165 | ||||
| 海豚社交网络 | 62 | 159 | 2 | BDSG | 4 | 0 | 0.773 5 | 149 |
| CPM | 4 | 34 | 0.408 8 | 175 | ||||
| k-dense | 4 | 34 | 0408 8 | 568 | ||||
| CPM+CE | 4 | 16 | 0.591 1 | 202 | ||||
| k-dense+CE | 4 | 16 | 0.591 1 | 599 | ||||
| 大学生足球网络 | 115 | 613 | 12 | BDSG | 12 | 0 | 0.639 0 | 480 |
| CPM | 13 | 2 | 0.595 1 | 920 | ||||
| k-dense | 12 | 2 | 0.637 0 | 1 860 | ||||
| CPM+CE | 13 | 0 | 0.601 0 | 1 028 | ||||
| k-dense+CE | 12 | 0 | 0.648 0 | 1 986 | ||||
| 电子邮件网络 | 1 133 | 5 451 | — | BDSG | 28 | 34 | 0.722 4 | 60 797 |
| CPM | 55 | 562 | 0.268 7 | 592 410 | ||||
| k-dense | 6 | 558 | 0.251 7 | 55 240 | ||||
| CPM+CE | 55 | 341 | 0.289 7 | 601 835 | ||||
| k-dense+CE | 6 | 14 | 0.503 4 | 63 938 | ||||
| 合作网络 | 1 589 | 2 742 | — | BDSG | 134 | 657 | 0.782 8 | 21 273 |
| CPM | 159 | 843 | 0.520 1 | 97 161 | ||||
| k-dense | 91 | 843 | 0.730 5 | 15 352 | ||||
| CPM+CE | 159 | 688 | 0.567 5 | 120 927 | ||||
| k-dense+CE | 91 | 790 | 0.763 1 | 23 451 |
实验结果表明BDSG算法在这些网络数据上均具有较好的性能表现。BDSG算法在空手道俱乐部和大学生足球网络上所得到社区个数与网络实际的社区个数相同,而电子邮件网络和合作网络缺乏原始社区个数信息,无法进行比较;海豚社交网络和大学生足球网络中,BDSG算法所用时间明显少于CPM与k-dense算法;在电子邮件网络和合作网络中,BDSG运行时间比k-dense算法慢,但最终未聚类结点数少于k-dense算法;在这些实验数据集上,本算法所产生的未聚类结点个数明显较少、社区模块性较高。
此外,本文给出的中心社区扩展算法也可应用于CPM、k-dense等算法以处理未聚类节点,提高聚类性能。实验结果(见表 2)表明CPM与k-dense算法的聚类有效性均显著提高。在空手道俱乐部、海豚社交网络、电子邮件网络和合作网络中,在CPM与k-dense算法运行时间略有增大的情况下,CE算法的加入使得其未聚类结点个数降幅较大,社区模块性具有较为明显的提高。同时CPM与k-dense算法在加入扩展策略CE之后与BDSG算法相比,BDSG算法在未聚类结点数以及社区模块性方面优势依然较为明显。
综上所述,BDSG算法在空手道俱乐部、海豚社交网络、大学生足球网络、电子邮件网络和合作网络等数据集上,与CPM、k-dense算法相比运行时间较短、未聚类结点个数较少、社区模块性较高,具有良好的聚类性能。同时,中心社区扩展算法可以有效地提高CPM、k-dense算法的聚类性能,该算法也可用于其他非结点完全覆盖算法。
5 结束语本文提出一种基于稠密子图的图聚类算法BDSG,解决了基于密度算法中大量未聚类结点问题。通过搜索网络中的相对稠密子图得到中心社区;通过定义结点对社区的归属度来度量结点和社区连接倾向性,进而给出一种中心社区扩展策略对中心社区外结点进行聚类。通过与CPM、k-dense算法在 5个真实网络数据集上进行分析比较,结果表明 ,BDSG算法在未聚类结点个数、模块性及运行时间方面均表现出较好的性能。同时中心社区扩展策略与其他算法相结合,对提高CPM、k-dense等算法的聚类性能具有一定的适用性。
| [1] | FORTUNATO S. Community detection in graphs[J]. Physics reports, 2010, 486(3/4/5): 75-174. |
| [2] | NEPUSZ T, YU Haiyuan, PACCANARO A. Detecting overlapping protein complexes in protein-protein interaction networks[J]. Nature methods, 2012, 9(5): 471-472. |
| [3] | DEYLAMI H A, ASADPOUR M. Link prediction in social networks using hierarchical community detection[C]//Proceedings of the 7th conference on information and knowledge technology. Urmia, Iran, 2015: 1-5. |
| [4] | SCHAEFFER S E. Graph clustering[J]. Computer science review, 2007, 1(1): 27-64. |
| [5] | 杨博, 刘大有, LIU Jiming, 等. 复杂网络聚类方法[J]. 软件学报, 2009, 20(1): 54-66. |
| [6] | 冀俊忠, 刘志军, 刘红欣, 等. 蛋白质相互作用网络功能模块检测的研究综述[J]. 自动化学报, 2014, 40(4): 577-593. |
| [7] | PALLA G, BARABáSI A L, VICSEK T. Quantifying social group evolution[J]. Nature, 2007, 446(7136): 664-667. |
| [8] | SIDIROPOULOS A, PALLIS G, KATSAROS D, et al. Prefetching in content distribution networks via web communities identification and outsourcing[J]. World wide web, 2008, 11(1): 39-70. |
| [9] | 陈克寒, 韩盼盼, 吴健. 基于用户聚类的异构社交网络推荐算法[J]. 计算机学报, 2013, 36(2): 349-359. |
| [10] | FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976. |
| [11] | NEWMAN M E J. Community detection and graph partitioning[J]. Europhysics letters, 2013, 103(2): 28003. |
| [12] | NEWMAN M E J. Spectral methods for community detection and graph partitioning[J]. Physical review E, 2013, 88(4): 042822. |
| [13] | LIN Chuncheng, KANG Jiarong, CHEN J Y. An integer programming approach and visual analysis for detecting hierarchical community structures in social networks[J]. Information sciences, 2015, 299: 296-311. |
| [14] | REN Jun, WANG Jianxin, LI Min, et al. Identifying protein complexes based on density and modularity in protein-protein interaction network[J]. BMC systems biology, 2013, 7(S4): S12. |
| [15] | LI Xiaoli, FOO C S, NG S K. Discovering protein complexes in dense reliable neighborhoods of protein interaction networks[C]//Proceedings of the computational systems bioinformatics conference. San Diego, USA, 2007, 6: 157-168. |
| [16] | PALLA G, DERéNYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435: 814-818. |
| [17] | SAITO K, YAMADA T, KAZAMA K. Extracting communities from complex networks by the k-dense method[J]. IEICE transactions on fundamentals of electronics, communications and computer sciences, 2008, E91-A(11): 3304-3311. |
| [18] | SUN Penggang, GAO Lin. Fast algorithms for detecting overlapping functional modules in protein-protein interaction networks[C]//Proceedings of the IEEE computational intelligence in bioinformatics and computational biology. Nashville, TN, USA, 2009: 247-254. |
| [19] | LIU Guimei, WONG L, CHUA H N. Complex discovery from weighted PPI networks[J]. Bioinformatics, 2009, 25(15): 1891-1897. |
| [20] | BADER G D, HOGUE C W V. An automated method for finding molecular complexes in large protein interaction networks[J]. BMC bioinformatics, 2003, 4(1): 2. |
| [21] | FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41. |
| [22] | CUI Yaizu, WANG Xingyuan, EUSTACE J. Detecting community structure via the maximal sub-graphs and belonging degrees in complex networks[J]. Physica A: statistical mechanics and its applications, 2014, 416: 198-207. |
| [23] | ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of anthropological research, 1977, 33(4): 452-473. |
| [24] | LUSSEAU D, SCHNEIDER K, BOISSEAU O J, et al. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations: Can geographic isolation explain this unique trait[J]. Behavioral ecology and sociobiology, 2003, 54(4): 396-405. |
| [25] | NEWMAN M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical review E, 2006, 74(3): 036104. |
| [26] | GUIMERà R, DANON L, DíAZ-GUILERA A, et al. Self-similar community structure in a network of human interactions[J]. Physical review E, 2003, 68(6): 065103. |
| [27] | NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical review E, 2004, 69(2): 026113. |
| [28] | SHEN Huawei, CHENG Xueqi, CAI Kai, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A: statistical mechanics and its applications, 2009, 388(8): 1706-1712. |



