2. 中山大学 数据科学与计算机学院, 广东 广州 510006;
3. 广东省信息安全技术重点实验室, 广东 广州 510006
2. School of Data and Computer Science, Sun Yat-sen University, Guangzhou 510006, China;
3. Guangdong Key Laboratory of Information Security Technology, Guangzhou 510006, China
聚类集成(clustering ensemble)的目标是融合多个聚类结果以得到一个更优的最终聚类结果[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]。每一个输入聚类称为一个聚类成员(ensemble member)或者基聚类(base clustering);聚类成员可以由不同聚类算法生成,或者由一个聚类方法在不同参数设定下生成。聚类成员的质量(或可靠度)是影响聚类集成性能的关键因素之一。然而,在无监督设定下,现有方法大多无法自动评估聚类成员可靠度并据此对其加权,从而容易受到低质量聚类成员(甚至病态聚类成员)的负面影响。近年来,部分研究者开始对此进行研究并提出了一些加权聚类集成的方法[8, 11],但是这些方法往往在集成效果和运算效率上仍有局限性。例如,文献[11]提出了一种基于非负矩阵分解的加权聚类集成方法,但该方法的非负矩阵分解过程运算负担非常大,基本无法应用于大数据集;文献[8]提出了一种基于归一化群体认可度指标的加权聚类集成方法,但较高的计算复杂度也是限制其更广泛应用的一个重要障碍。在当前聚类集成研究中,如何高效地对聚类成员的可靠度进行评估并加权集成,仍是一个非常具有挑战性的问题。
针对此问题,本文提出了一种基于二部图构造和决策加权机制的聚类集成算法。我们将每个聚类成员视作一个包含若干连接决策的集合。每个聚类成员的决策集合享有一个单位的可信度,该可信度由集合内的各个决策共同分享。进一步,我们根据每个聚类成员的每个决策分享得到的可信度进行加权,并将之整合至一个二部图模型,进而利用快速二部图分割算法将该图划分为若干块以得到最终聚类结果。我们将本文方法及多个对比方法在8个实际数据集上进行实验分析,实验结果表明,本文方法相较于其他对比方法在聚类集成效果及运算效率上均表现出显著优势。
1 相关研究现有的聚类集成方法,主要可以分为3类:1)基于点对相似性的方法[4, 5];2)基于图分割的方法[1, 3];3)基于中心聚类的方法[2, 6]。
基于点对相似性的方法[4, 5]根据数据点与数据点之间在多个聚类成员中属于相同簇的频率来得到一个共联矩阵,并以该共联矩阵作为相似性矩阵,进而采用层次聚类方法得到最终聚类结果。文献[4]最早提出共联矩阵的概念,并提出了线索集聚聚类(evidence accumulation clustering,EAC)方法。文献[5]对EAC方法进行扩展,将簇的大小加入考虑,提出了概率集聚算法。
基于图分割的方法[1, 3]首先根据聚类集成信息构造一个图结构,再利用图分割算法将图划分为若干块,进而得到最终的聚类集成结果。文献[1]将聚类集成中的每一个簇视作一条超边,构造得到一个超图结构,进而可使用METIS算法[12]或Ncut算法[13]将其分割为若干块,以得到最终聚类结果。
基于中心聚类的方法[2, 6]将聚类集成问题建模为一个最优化问题,其优化目标是寻找一个与所有聚类成员的相似性最大化的聚类结果。中心聚类问题是一个NP难问题[14],因而在全局聚类空间寻找最优解对于较大的数据集是几乎不可行的。针对此问题,文献[2]将聚类表示为染色体,并提出利用遗传算法求得一个近似解。文献[6]提出一种基于2-D串编码的一致性度量,并利用0-1半正定规划来最大化此一致性度量,以得到中心聚类。
尽管国内外研究者已经提出了许多聚类集成算法[1, 2, 3, 4, 5, 6],但这些算法大都将各个聚类成员同等对待,缺乏对聚类成员进行可靠度估计及加权的能力,容易受低质量聚类成员(甚至病态聚类成员)的负面影响。针对此问题,近年来有研究者提出了一些解决方法[8, 11]。文献[11]提出了一种基于非负矩阵分解的加权聚类集成方法,在该方法的优化过程中,可对各聚类成员的可靠度进行估计并加权;但是,该方法的非负矩阵分解过程的耗时非常大,使其无法应用于较大数据集。文献[8]利用归一化群体认可度指标对各个聚类成员的可靠度进行估计,并进而提出了两个加权聚类集成算法;但是归一化群体认可度指标的计算复杂度较高,使其难以适用于大规模数据的聚类集成问题。在当前聚类集成研究中,如何有效地、高效地估计聚类成员可靠度并据此加权集成,进而提高聚类集成性能,仍是一个亟待解决的挑战性问题。
2 基于决策加权的聚类集成算法 2.1 问题建模
给定一个数据集X=x1,x2,…,xN,其中xi表示X中的第i个数据点,N表示X中数据点的个数。令Π表示一个包含M个聚类成员的集合,记作
Π=π1,π2,…,πM
πm=Cm1,Cm2,…,Cmnm
C=C1,C2,…,CNc
聚类集成的目标是将聚类集合Π中各聚类成员的信息融合得到一个更优、更鲁棒的聚类结果。根据输入信息的不同,聚类集成问题主要有2种不同的建模方式:第1种建模方式同时以聚类集合Π和数据集X作为输入信息[15, 16, 17];第2种建模方式则只以聚类集合Π为输入信息,而不需要访问数据集X中的数据特征[1 -10]。两种建模方式的区别就在于除聚类成员的信息之外是否可访问原始数据特征。在聚类集成研究中,第2种建模方式对原始数据的依赖度更低,亦被更广泛采用[1, 2, 3, 4, 5, 6, 7, 8, 9, 10];本文的聚类集成研究按照第2种建模方式进行,即以聚类集合Π为输入,不要求访问原始数据特征,依此得到最终聚类结果π*。
2.2 决策加权
在聚类集成问题中,每一个聚类成员可以视作是一个包含若干个连接决策的集合。如果数据点
xi和xj在聚类成员πm中被划分在同一个簇,那么我们称πm对xi和xj作出了一个连接决策,由此可得一个簇Cmk∈πm所作出的连接决策的数量为
#Decisions(Cmk)=$\frac{\left( 1-\left| C_{k}^{m} \right| \right)\left| C_{k}^{m} \right|}{2}$
#Decisions(πm)=$\sum\limits_{k=1}^{{{n}^{m}}}{{}}$#Decisions(Cmk)
(1)
每个聚类成员包含一定数量的连接决策;聚类成员的可靠度估计与加权问题,可视作是对聚类成员连接决策的可靠度估计与加权问题。我们在实例研究中发现,聚类成员的可靠度与其连接决策总数存在显著的负相关关系。
具体地,我们以MNIST数据集[18]为例。该数据集包含5 000个数据点。我们使用k均值聚类算法为该数据集生成100个聚类成员,每次生成均采用随机聚类个数及随机初始化。如果两个数据点xi
和xj在聚类成员πm中被划分在同一个簇,并且这两个数据点在MNIST数据集的真实类别中也属于同一个类,那么称聚类成员πm对数据点xi和xj作出了一个正确决策,并将πm作出的正确决策的数量记作
#CorrectDecisions(πm)。我们将聚类成员πm作出的所有连接决策中正确决策所占的比例,称为正确决策率,记作RatioCD
(πm),计算公式为
RatioCDπm=$\frac{\#CorrectDecisions\left( {{\pi }^{m}} \right)}{\#Decisions\left( {{\pi }^{m}} \right)}$
(2)
图 1显示了MNIST数据集的100个聚类成员的连接决策数与正确决策率之间的关系。对每一个聚类成员,根据式(1)计算其连接决策数,根据式(2)计算其正确决策率,从而在图 1中描出对应的坐标点。由图 1可以看到,聚类成员的连接决策数与其正确决策率存在显著的负相关关系。此实验结论的直观理解在于,若一个聚类成员作出的连接决策数量越小(即越稀有),则其正确率往往越高(即越宝贵);若其连接决策数量越大,则其决策出错的比例往往越高。当一个聚类成员将全体数据点都归入同一个簇时,其连接决策数达到最大值,此时该聚类成员的连接决策失去意义。

|
| 图 1 对于MNIST数据集,各聚类成员的连接决策数与正确决策率之间的关系 Fig. 1 The relation between #Decisions and RatioCD for the MNIST dataset |
一个聚类成员的正确决策率,是其对于数据点两两之间处于同一个簇的判断的正确比例,可视作该聚类成员的可靠度。由于聚类决策数与可靠度的负相关关系,为减小低可靠度决策的不良影响以提高聚类集成鲁棒性,一个可行策略是采取权值与聚类决策数负相关的加权集成方案。在本文中,我们对每个聚类成员分配一个单位的可信度,该可信度由聚类成员内的全体决策共同分享。那么,聚类成员
πm中每个连接决策分享到的可信度是1/#Decisions(πm)个单位。根据各个聚类成员中连接决策的平均可信度对其加权,则聚类成员πm的权值计算公式为
wπm=$\frac{\frac{1}{\#Decisions\left( {{\pi }^{m}} \right)}}{\sum\limits_{{}}^{{}}{_{k=1}^{M}}\frac{1}{\#Decisions\left( {{\pi }^{m}} \right)}}$
进而可得:
wπm=$\frac{1}{\#Decisions\left( {{\pi }^{m}} \right)\sum\limits_{{}}^{{}}{_{k=1}^{M}}\frac{1}{\#Decisions\left( {{\pi }^{m}} \right)}}$
(3)
$\sum\limits_{m=1}^{M}{w\left( {{\pi }^{m}} \right)}=1$
在聚类成员可靠度分析与权值分配的基础上,我们将进一步将聚类集成问题构造为一个二部图模型。在所构造的二部图模型中,聚类集合中各个聚类成员的簇与数据点同时作为节点。簇节点与簇节点之间不存在连接边;数据点节点与数据点节点之间亦不存在连接边。两个节点之间存在连接边,当且仅当其中一个节点是数据点节点,另一个节点是簇节点,并且该数据点位于该簇之内。边的权值由该簇所在的聚类成员的权值决定(见式(3))。由此,可得到一个二部图结构,其左部为数据点节点的集合,右部为簇节点的集合。我们将该二部图结构表示
为
G=(U,V,E)
${{e}_{ij}}=\left\{ \begin{matrix}
w\left( \pi \left( {{v}_{j}} \right) \right), & {{u}_{i}}\in X,{{v}_{j}}\in C,{{u}_{i}}\in {{v}_{j}} \\
0, & 否则 \\
\end{matrix} \right.$
接下来,利用图G的二部图结构,我们采用Tcut算法[19]将图G快速地分割为若干块,进而将每一块中数据点集合作为最终聚类的一个簇,由此可以得到最终聚类结果。
2.4 时间复杂度第2.3节所构造的二部图G包含有 N+Nc个节点,其中N是数据点个数,Nc是簇个数。如果使用经典的Ncut算法[19]对图G进行分割,其时间复杂度是O(k(N+Nc)3/2),其中k是图分割的块数。与之相比,本文采用的Tcut算法[19]可利用图 G的二部图结构,进行快速图分割,其时间复杂度是 O(kN+kNc3/2) ;考虑式(3)中权值计算的复杂度是ON,故本文总体算法的时间复杂度即是O(kN+kNc3/2)。由于在实际聚类问题中数据点个数N通常远大于簇个数Nc,因此使用 Tcut算法相当于可使时间复杂度由O(kN3/2)降低至O(kN)。当面对大数据集时,本文算法在运算效率上的优势尤其显著;在本文后续的对比实验中,本文聚类集成算法相比于现有算法的效率优势也得到了验证。
3 实验结果与分析在本节中,我们将在多个实际数据集中进行实验,与若干现有聚类集成算法进行对比分析,以验证本文方法的有效性及运算效率。
3.1 数据集本文的实验一共使用了8个实际数据集,分别是Glass、 Ecoli、 Image Segmentation(IS)、 MNIST、 ISOLET、 Pen Digits(PD)、 USPS以及Letter Recognition(LR)。其中,除MNIST数据集来自于文献[18]之外,其他7个数据集均来自于UCI机器学习数据仓库(UCI machine learning repository)[20]。所用的测试数据集的具体情况如表 1所示。
| 数据集 | 数据点数 | 维度 | 类别数 |
| Glass | 214 | 9 | 7 |
| Ecoli | 336 | 7 | 8 |
| IS | 2 310 | 19 | 7 |
| MNIST | 5 000 | 784 | 10 |
| ISOLET | 7 797 | 617 | 26 |
| PD | 10 992 | 16 | 10 |
| USPS | 11 000 | 256 | 10 |
| LR | 20 000 | 16 | 26 |
在本文实验中,我们首先需要生成一个包含若干聚类成员的聚类集合,以对比分析本文方法以及其他聚类集成方法的聚类效果。具体地,我们在每一次运行中使用k均值聚类算法生成M个聚类成员,每一个聚类成员的生成均采用随机初始化,并在区间[2,$\sqrt{N}$]中随机选取初始聚类个数k。对于每一个方法在每一个数据集上的实验,我们均运行10次(每次使用随机生成的聚类集合,如前所述),然后得到各个方法的平均性能得分,以实现客观公平的对比与分析。
我们将聚类成员个数M称为聚类集成规模;将数据集的数据点数N称为数据规模。在后续实验中,我们首先固定聚类集成规模M=10,接下来分别进行本文方法与聚类成员以及与其他聚类集成方法的对比实验,并进一步测试在不同聚类集成规模M下各个聚类集成方法的聚类表现。最后,将对比测试各个聚类集成方法的运算效率。在本文实验中,采用标准互信息量(normalized mutual information,NMI)[1]作为评价指标。NMI可根据两个聚类之间的互信息量来度量其相似性,是聚类研究中被广泛应用的一个评价指标。一个聚类结果(与真实聚类比较)的NMI值越大,则表示其聚类质量越好。
3.3 与聚类成员的对比实验
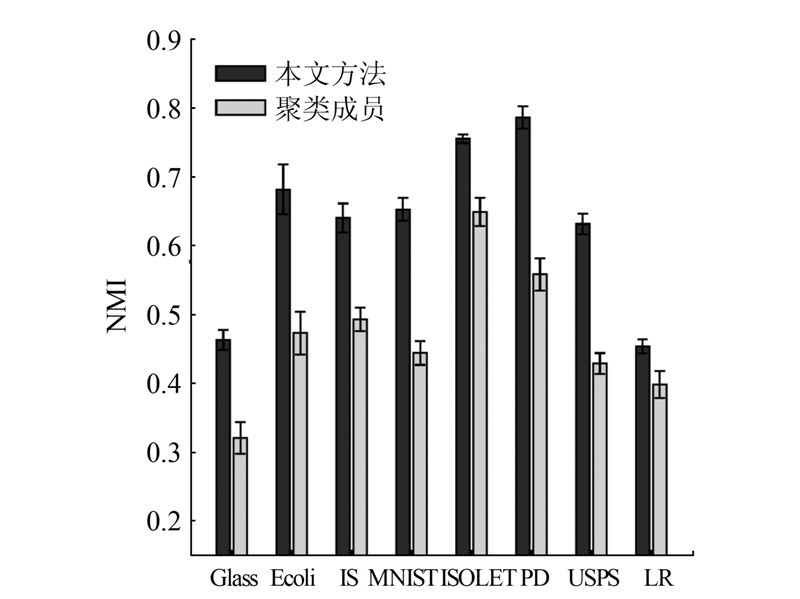
聚类集成的目标是融合多个聚类成员的信息以期得到一个更优聚类。在本节中,我们将本文方法的聚类集成结果,与聚类成员进行对比实验。在每个数据集上均测试10次;每次测试均随机生成一个包含M个聚类成员的聚类集合,然后在此聚类集合上运行本文算法以得到一个集成聚类结果。由此,得到本文方法在10次运行测试中的平均表现以及聚类成员的平均表现(以NMI度量)。如图 2所示。
|
| 图 2 本文方法与聚类成员的性能对比 Fig. 2 Comparison between our method and the base clusterings |
本文方法可取得比聚类成员更好的聚类结果;尤其是在Glass、Ecoli、 IS、MNIST、PD、USPS等数据集,本文方法相较聚类成员优势更显著。
3.4 聚类集成方法的对比实验本节将所提出方法与6个现有的聚类集成方法 进行对比实验。这6个对比方法分别是evidence accumulation clustering(EAC)[4]、hybrid bipartite graph formulation(HBGF)[3]、SimRank similarity based method(SRS)[21]、weighted connected triple based method(WCT)[22]、weighted evidence accumulation clustering(WEAC)[8]以及graph partitioning with multi-granularity link analysis(GP-MGLA)[8]。
在每一个数据集中,每个聚类集成方法均运行10次,每次运行根据第3.2节所述随机生成聚类成员,进而得到每个算法在每个数据集的平均NMI得分及其标准差。在表 2中,在每一个数据集中,最高NMI得分以粗体显示。如表 2所示,本文方法在8个数据集上均取得了优于其他聚类集成方法的聚类效果,特别是在Glass、MNIST和USPS数据集上,本文方法取得的平均NMI得分比其他方法高出10%左右。表 2的对比实验结果验证了本文方法在聚类集成效果上的优势。
| 测试方法 | Glass | Ecoli | IS | MNIST | ISOLET | PD | USPS | LR |
| 本文方法 |
|
|
|
|
|
| ||
| EAC [4] | 0.418 | 0.640 | 0.618 | 0.592 | 0.746 | 0.747 | 0.580 | 0.435 |
| HBGF [3] | 0.397 | 0.635 | 0.624 | 0.609 | 0.747 | 0.757 | 0.588 | 0.441 |
| SRS [21] | 0.423 | 0.632 | 0.623 | 0.594 | 0.747 | 0.755 | 0.593 | 0.436 |
| WCT [22] | 0.434 | 0.678 | 0.623 | 0.627 | 0.752 | 0.764 | 0.598 | 0.439 |
| WEAC [8] | 0.409 | 0.637 | 0.616 | 0.607 | 0.746 | 0.752 | 0.581 | 0.439 |
| GP-MGLA[8] | 0.399 | 0.640 | 0.634 | 0.624 | 0.747 | 0.758 | 0.602 | 0.441 |
接下来,我们进行本文方法与其他对比方法在不同聚类集成规模(即聚类成员个数)下的对比实验。当聚类集成规模由M=10增长到50时,各个聚类集成方法在10次运行中的平均NMI得分如图 3所示。在Ecoli数据集中,WCT方法取得了与本文方法基本相当的性能表现。除了Ecoli数据集之外,在其他7个数据集中,本文方法在不同聚类集成规模下的聚类表现均显著优于其他方法。图 3的实验结果验证了本文方法在不同聚类集成规模下表现出比其他聚类集成方法更好的鲁棒性。

|
| 图 3 各个方法的聚类集成性能 Fig. 3 The performances of different clustering ensemble methods with varying ensemble sizes |
在本节中,我们进行各个聚类集成方法的运行时间对比实验。所有实验均在MATLAB 2014b下运行,所使用的工作站配置具体如下:Windows Server 2008 R2 64位操作系统;英特尔八核心2.4 GHz中央处理器;96 GB内存。为求客观对比各个算法运行的CPU时间,所有实验均在单线程模式下运行。
为测试各个聚类集成算法在不同数据规模(即数据点个数)下的运行时间,本节实验在LR数据集的不同大小的子集上进行。LR数据集一共包含有2万个数据点;我们在实验中所测试的子集大小从0逐步增长至20 000。例如,当测试数据规模设定为N′∈0,20 000时,我们就随机从整个LR数据集中选取N ′个数据点进行实验,并记录各个测试方法在此数据规模上的运行时间。如图 4所示,当数据规模较小时,HBGF、EAC、WEAC以及本文方法均有较高运算效率。而当数据规模继续增长时,本文方法相对于其他方法的效率优势开始变大。对于整个LR数据集20 000个数据点的规模,本文方法仅需要6.19 s;除本文方法之外,其他对比方法之中最快的3个方法(HBGF、EAC和WEAC)则分别需要12.18、34.48和33.87 s的运算时间。图 4验证了本文方法的优势。

|
| 图 4 各个聚类集成方法在不同数据规模下的运行时间对比 Fig. 4 Execution time of different methods with varying data sizes |
为解决聚类集成研究中的聚类成员可靠度估计与加权问题,本文提出了一个基于二部图结构与决策加权机制的聚类集成方法。我们将每个聚类成员视作一个包含若干连接决策的集合,并为每个聚类成员的决策集合分配一个单位的可信度。该可信度由聚类成员内的各个决策共同分享。进一步地,我们提出基于可信度分享的决策加权机制,并将之整合至一个统一的二部图模型中。因其二部图结构,该图模型可利用Tcut算法进行快速分割,从而得到最终聚类集成结果。本文在8个实际数据集中进行了实验,将所提出方法与聚类成员以及6个现有方法进行了对比分析。实验结果验证了本文方法在聚类质量及运算效率上的显著优势。
| [1] | STREHL A, GHOSH J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. The journal of machine learning research, 2003, 3(3): 583-617. |
| [2] | CRISTOFOR D, SIMOVICI D. Finding median partitions using information-theoretical-based genetic algorithms[J]. Journal of universal computer science, 2002, 8(2): 153-172. |
| [3] | FERN X Z, BRODLEY C E. Solving cluster ensemble problems by bipartite graph partitioning[C]//Proceedings of the 21st International Conference on Machine Learning. New York, NY, USA, 2004. |
| [4] | FRED A L N, JAIN A K. Combining multiple clusterings using evidence accumulation[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(6): 835-850. |
| [5] | WANG Xi, YANG Chunyu, ZHOU Jie. Clustering aggregation by probability accumulation[J]. Pattern recognition, 2009, 42(5): 668-675. |
| [6] | SINGH V, MUKHERJEE L, PENG Jiming, et al. Ensemble clustering using semidefinite programming with applications[J]. Machine learning, 2010, 79(1/2): 177-200. |
| [7] | HUANG Dong, LAI Jianhuang, WANG Changdong. Exploiting the wisdom of crowd: a multi-granularity approach to clustering ensemble[C]//Proceedings of the 4th International Conference on Intelligence Science and Big Data Engineering. Beijing, China, 2013: 112-119. |
| [8] | HUANG Dong, LAI Jianhuang, WANG Changdong. Combining multiple clusterings via crowd agreement estimation and multi-granularity link analysis[J]. Neurocomputing, 2015, 170: 240-250. |
| [9] | HUANG Dong, LAI Jianhuang, WANG Changdong. Ensemble clustering using factor graph[J]. Pattern recognition, 2016, 50: 131-142. |
| [10] | HUANG Dong, LAI Jianhuang, WANG Changdong. Robust ensemble clustering using probability trajectories[J]. IEEE transactions on knowledge and data engineering, 2016, 28(5): 1312-1326. |
| [11] | LI Tao, DING C. Weighted consensus clustering[C]//Proceedings of the 2008 SIAM International Conference on Data mining. Auckland, New Zealand, 2008: 798-809. |
| [12] | KARYPIS G, KUMAR V. Multilevel k-way partitioning scheme for irregular graphs[J]. Journal of parallel and distributed computing, 1998, 48(1): 96-129. |
| [13] | NG A Y, JORDAN M I, WEISS Y. On spectral clustering: Analysis and an algorithm[C]//Advances in Neural Information Processing Systems. Vancouver, Canada, 2001. |
| [14] | TOPCHY A, JAIN A K, PUNCH W. Clustering ensembles: models of consensus and weak partitions[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(12): 1866-1881. |
| [15] | VEGA-PONS S, CORREA-MORRIS J, RUIZ-SHULCLOPER J. Weighted partition consensus via kernels[J]. Pattern recognition, 2010, 43(8): 2712-2724. |
| [16] | VEGA-PONS S, RUIZ-SHULCLOPER J, GUERRA-GANDóN A. Weighted association based methods for the combination of heterogeneous partitions[J]. Pattern recognition letters, 2011, 32(16): 2163-2170. |
| [17] | 徐森, 周天, 于化龙, 等. 一种基于矩阵低秩近似的聚类集成算法[J]. 电子学报, 2013, 41(6): 1219-1224.XU Sen, ZHOU Tian, YU Hualong, et al. Matrix low rank approximation-based cluster ensemble algorithm[J]. Acta electronica sinica, 2013, 41(6): 1219-1224. |
| [18] | LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. |
| [19] | LI Zhenguo, WU Xiaoming, CHANG S F. Segmentation using superpixels: a bipartite graph partitioning approach[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA, 2012: 789-796. |
| [20] | BACHE K, LICHMAN M. UCI machine learning repository[EB/OL]. (2013-04-04). http://archive.ics.uci.edu/ml. |
| [21] | IAM-ON N, BOONGOEN T, GARRETT S. Refining pairwise similarity matrix for cluster ensemble problem with cluster relations[C]//Proceedings of the 11th International Conference on Discovery Science. Budapest, Hungary, 2008: 222-233. |
| [22] | IAM-ON N, BOONGOEN T, GARRETT S, et al. A link-based approach to the cluster ensemble problem[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(12): 2396-2409. |



