蛋白质组学是研究细胞内表达的所有的蛋白质及其变化规律的一门新兴学科[1]。蛋白质组主要是指由一个基因组,或一个细胞组织表达的所有蛋白质。基因组基本是固定不变的,而蛋白质组却为动态的,具有时空性和可调节性,能反映出特定基因的表达时间、表达量以及蛋白质翻译后的加工修饰等信息。蛋白质组学的研究试图比较细胞在不同生理或病理条件下蛋白质表达的异同,从整体上研究细胞或组织内蛋白质的组成及其活动规律。 蛋白质组学的一个重要目标是能够快速准确地进行蛋白质鉴定,即确定一个样本中真实存在的蛋白质。只有鉴定到生物样品中真实表达的蛋白质,才能准确地对蛋白质进行定量以及推断出蛋白质之间相互作用关系(protein-protein interaction,PPI),为进一步的疾病标记物发现和新药开发提供有力的支持[2]。因此,蛋白质鉴定是蛋白质组学研究的基础,对整个领域的进一步发展和应用有着十分重要的意义。
在高通量蛋白质组学研究中,目前使用的主流技术是质谱分析法(MS)[3],即用电场和磁场将运动的离子按它们的质荷比分离后进行检测。同时,为了从混合物样本中分离出蛋白质和肽段以便深入研究,液相色谱技术(LC)也被引入蛋白质鉴定,最终形成了LC-MS技术[4]。在LC-MS的基础上,鸟枪法蛋白质组学是蛋白质鉴定最常用的策略[5]。鸟枪法蛋白质组学的基本流程如下:1)蛋白质样本通过酶切消化等生物实验获得肽段的混合物溶液;2)将所得混合物进行离子化并使用质谱仪进行串联质谱分析,从而得到一系列的串联质谱(MS/MS)数据;3)对串联谱图进行预处理后通过肽段鉴定和蛋白质推断得到样本中可能存在的肽段和蛋白质。其大体流程如图 1所示。

|
| 图 1 鸟枪法蛋白质组学的基本流程 Fig. 1 The entire workflow of shotgun proteomics |
到目前为止,研究人员已经提出许多成熟可用的蛋白质推断算法[6, 7, 8, 9, 10]。关于这些方法的细节以及蛋白质推断过程中所遇到的问题挑战,读者可以参阅最近的综述文章[11, 12, 13]。总体来说,可以把蛋白质推断问题的输入抽象成一个二分图,如图 2(a)所示,其中一侧是候选蛋白质集合,另一侧是鉴定肽集合。例如,ProteinPropphet[6]、 IDPicker[10]均使用标准二分图作为输入,通过建立不同的假设来设计模型和算法。在二分图模型中,由于输入被限制,所以无论算法多么完美,结果还是无法进一步完善。因此为了提高蛋白质鉴定的准确率,研究人员尝试引入一些额外信息。借用额外信息改变传统的蛋白质推断问题的输入,即在原来的标准二分图输入的基础上,加入额外信息,例如原始串联质谱和一级质谱、蛋白质相互作用网络、mRNA表达信息等。图 2(b)所示为引入质谱数据后的三层图模型。

|
| 图 2 标准的二分图和引入额外信息的图结构 Fig. 2 The standard bipartite graph and the graph when introducing extra information |
蛋白质推断问题的一个最大的挑战来自于肽段的退化,也称共享肽段问题,即一个鉴定肽段被多个候选蛋白质所共享。蛋白质推断算法的优劣主要取决于它是否能准确地找出哪些或者哪个蛋白质真正地产生共享的肽段。目前为止,研究人员已经开发出很多蛋白质推断算法,如ProteinProphet、MSBayesPro[9]和Fido[7]等。虽然这些算法使用多种不同的方式来解决肽段退化问题,但都存在着一些固有的缺陷。ProeinProphet使用一个类期望最大化的迭代过程来估计蛋白质存在的概率,该方法没有明确定义如何优化模型中计算蛋白质概率的公式。相反地,MSBayesPro、HSM[8] 和Fido都是从清晰准确的统计假设中推导出公式的,但是,这些方法获得最优解的过程是很费时的。
基于此,本文提出了一种基于概率图模型的方法来解决蛋白质推断问题。本文的主要着眼点放在两个问题上,一个是概率图模型在蛋白质推断问题上的应用,另一个是串联质谱数据对于蛋白质存在概率的影响。前者将蛋白质推断问题抽象成一个概率图模型的求解问题,鉴定到的肽段以及候选蛋白质都抽象为节点,候选蛋白质及其对应肽段之间的关系抽象为有向边,这样就可以抽象成一个有向的二部图;后者主要是考虑肽鉴定过程中谱与肽段之间指派的正确性的影响,也可称作肽段识别概率,是指鉴定肽在样本中存在的后验概率,作为本文概率图模型的输入。
1 基于概率图模型的蛋白质推断算法 1.1 算法介绍概率图模型是由图论和概率论结合而成的描述多元统计关系的有效模型[14],它为多个变量之间复杂的依赖关系的表示提供了统一的框架,具有紧凑有效、简洁直观的特点。其在计算机视觉、生物信息学、自然语言处理等领域都有广泛的应用。
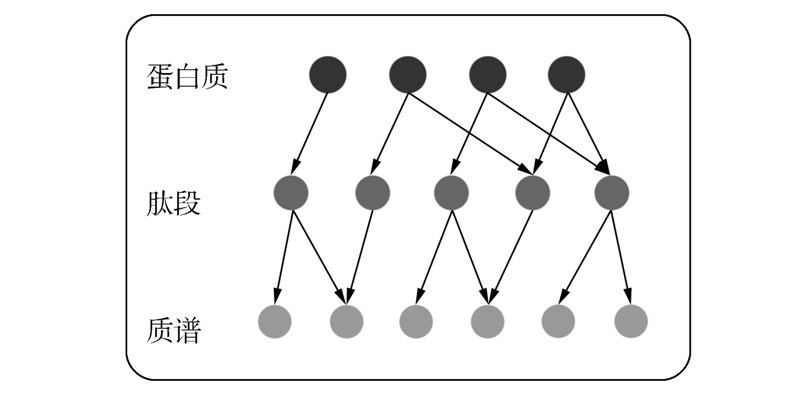
本文提出了基于概率图模型的蛋白质推断算法(PGMPi),该方法主要将概率图模型应用到蛋白质推断问题上,同时引入肽鉴定过程中谱与肽段之间指派的正确性的影响。由于蛋白质推断输入数据是一个二部图,一侧为候选蛋白质的集合,另一侧为肽段集合。本文将肽段以及候选蛋白质都抽象为节点,候选蛋白质及其对应肽段之间的关系抽象为有向边,这样就可以抽象成一个有向的二部图;同时考虑串联质谱数据对于蛋白质概率的影响,也将质谱数据抽象为节点,肽段和其对应谱图之间存在一个有向边,这样就得到一个三层的有向图结构,从而将蛋白质鉴定问题抽象为概率图求解问题,如图 3所示。
|
| 图 3 引入质谱信息的三层图结构 Fig. 3 The three-layer graph when introducing the MS/MS data |
本文算法基于有向图模型,也称为贝叶斯网络[15]。需明确的是,模型的目标是从候选蛋白质集合中找到真正存在于样本中的蛋白质子集。根据这一目标,本文首先给出了一个图中所有节点联合概率分布,即谱图、肽段及其对应候选蛋白质同时存在于样本中的概率。由于有向图采用乘积法则,对于x→y,联合概率分布为px,y)(=p(x)p(y|x)。其次对该联合概率分布提出一些基本假设,如蛋白质之间相互独立、每个鉴定肽打分之间相互独立等,并根据这些假设条件做简单的数学变换确定参数变量,之后根据联合概率分布给出蛋白质的后验概率公式,由于求解具有最大联合概率分布的候选蛋白质问题规模较大,暴力求解的代价十分昂贵,故本文采用了吉布斯抽样来获得具有最大后验的最优蛋白质配置。
相关符号及其定义在表 1中给了详细的说明。
| 符号 | 说明 |
| X | 候选蛋白质集合 |
| x1,x2,…,xm | 指示变量,如果xi=1,蛋白质i存在,否则为不存在 |
| Y | 鉴定得到的肽段集合 |
| y1,y2,…,yn | 指示变量,如果yj=1,肽段j存在,否则不存在 |
| S | 质谱仪产生的谱图信息对应的打分 |
| s1,s2,…,sn | 每个肽段j对应一个打分sj |
| Nj | 可以生成肽段j的候选蛋白质的集合 |
| Mi | 候选蛋白质i可以产生的肽段的集合 |
| Gi | 蛋白质i所存在组的蛋白质集合 |
| gj | 肽段j所存在组的肽段的集合 |
蛋白质、肽段以及质谱的联合概率公式为
P(X,Y,S)=P(x1,…,xm)·P(y1,…,yn|x1,…,xm)·
P(s1,…,sn|y1,…,yn)
(1)
1) 假设两个候选蛋白质之间相互独立:
P(x1,x2,…,xm)=$\prod\limits_{i=1}^{m}{{}}$p(xi)
(2)
2) 假设不同的蛋白质对于其对应鉴定肽的贡献是独立的;
P(y1,y2,…,yn|x1,x2,…,xm)=
$\prod\limits_{j}{{}}$[1-P(yj=1|x1,x2,…,xm)]1-yj·
P(jy=1|x1,x2,…,xm)yj=
$\prod\limits_{j}{{}}$[$\prod\limits_{i\in {{N}_{j}}}^{{}}{{}}$(1-α)xi]1-yj[1-$\prod\limits_{i\in {{N}_{j}}}^{{}}{{}}$(1-α)xi]yj
(3)
P(y1,y2,…,yn|x1,x2,…,xm)=$\prod\limits_{j}{{}}${(1-yj)[$\prod\limits_{i\in {{N}_{j}}}^{{}}{{}}$(1-α)xi]+yj[1-$\prod\limits_{i\in {{N}_{j}}}^{{}}{{}}$(1-α)xi]}
(4)
P(yj|x1,…,xm)=
(1-yj)[$\prod\limits_{i\in {{N}_{j}}}^{{}}{{}}$(1-α)xi]+yj[1-$\prod\limits_{i\in {{N}_{j}}}^{{}}{{}}$(1-α)xi]
(5)
3) 欲求得可能存在于样本中的蛋白质子集,需使得联合概率最大化。模型可以转化为寻找最大后验蛋白质配置的问题,对于每个蛋白质的后验概率:
P(xi|S)=$\frac{\sum\limits_{X:{{x}_{i}}=1}^{{}}{\prod\limits_{{{x}_{i}}}{p\left( {{x}_{i}} \right)}\prod\limits_{j\in {{M}_{i}}}{P\left( {{y}_{j}}\left| X \right. \right)\prod\limits_{j\in {{M}_{i}}}{P\left( {{y}_{j}}\left| {{s}_{j}} \right. \right)}}}}{\sum\limits_{X}^{{}}{\prod\limits_{{{x}_{i}}}{p\left( {{x}_{i}} \right)}\prod\limits_{j\in {{M}_{i}}}{P\left( {{y}_{j}}\left| X \right. \right)\prod\limits_{j\in {{M}_{i}}}{P\left( {{y}_{j}}\left| {{s}_{j}} \right. \right)}}}}$
(6)
4)根据以下规定,将蛋白质和肽段进行分组。
①在同一组中任意两个元素之间至少存在一条路径;
②除去组中的肽段之外,对于组中的蛋白质没有其他的肽段被鉴定到;
③没有其他的蛋白质可以生成组中的肽段。
P(xi|S)=$\frac{\sum\limits_{X:{{x}_{i}}=1}^{{}}{\prod\limits_{l:{{G}_{l}}={{G}_{l}}}{p\left( {{x}_{i}} \right)}\prod\limits_{j\in {{g}_{i}}={{G}_{i}}}{P\left( {{y}_{j}}\left| X \right. \right)\prod\limits_{j\in {{g}_{i}}={{G}_{i}}}{P\left( {{y}_{j}}\left| {{s}_{j}} \right. \right)}}}}{\sum\limits_{X}^{{}}{\prod\limits_{l:{{G}_{l}}={{G}_{l}}}{p\left( {{x}_{i}} \right)}\prod\limits_{j\in {{g}_{i}}={{G}_{i}}}{P\left( {{y}_{j}}\left| X \right. \right)\prod\limits_{j\in {{g}_{i}}={{G}_{i}}}{P\left( {{y}_{j}}\left| {{s}_{j}} \right. \right)}}}}$
(7)
模型的主要目标为寻找一个具有最大后验的蛋白质配置,也就是最大化每个蛋白质后验概率P(Xi|S),从而推断出真实存在于样本中的蛋白质集合。
1.3 模型求解给定蛋白质的配置图,以及肽段被正确识别的概率sj,在参数α确定的情况下,根据式(7)可直接计算出蛋白质的后验概率。但是这种暴力求解方法的时间复杂度为O(2m),由于图的规模较大,所以直接暴力求解的代价是十分昂贵的,故本文采用了吉布斯抽样[16]来获得具有最大后验的最优蛋白质配置。
吉布斯抽样是马尔可夫蒙特卡罗(Markov Chain monte Carlo,MCMC)算法中的特例,用来构造多变量概率分布的随机样本。考虑具有p(z)=p(z1,z2,…,zm)分布的样品集,并且给定一些符合马尔可夫性质的初始状态。吉布斯抽样的每一步骤都会根据剩余变量的当前状态值更新其中一个变量的状态值。也就是说,对于z的第i个组件zi 可以通过计算p(zi|z\i)得到,其中z\i表示除zi的所有组件。迭代这一过程在每一步使用一个转变函数来更新变量信息,直到收敛为止。
将该方法用于求解蛋白质推断问题,大大降低了求解模型(PGMPi)的时间复杂度,算法收敛所得的蛋白质后验概率即为该蛋白质真实存在于样本中的概率。需要说明的是,该方法所求的解为近似最优解,但可以通过改变收敛的判断标准来对近似解调优。
2 实验及结果评估为了验证本文提出的蛋白质推断算法PGMPi的表现,选取2个典型的蛋白质推断算法MSBayesPro,Fido在6个数据集上进行比较实验。
2.1 数据集本文选取了6个公开的数据集来验证PGMPi的表现:18 mixtures[17],Sigma49[18],Yeast[19],DME[20],HumanMD[21]和HumanEKC[19]。它们主要分为2类:有参考集的数据集和无参考集的数据集。前3个数据集都拥有相对应的蛋白质参考数据集,即预先知道的存在于样本中的蛋白质集合。另3个数据集则不拥有这样的参考集。关于这些数据集的更多细节详情请参见文献[22]。
本文采用广泛使用的目标-诱饵的策略来评估算法的表现。该策略的主要思想为:在包含所有目标蛋白质序列以及等量的诱饵蛋白质序列的混合蛋白质数据库中搜索串联质谱;当鉴定得到的蛋白质存在于蛋白质参考集或者来自于目标蛋白质数据库时,该蛋白质被认为是正确的鉴定结果。
2.2 参数设置实验使用的数据库搜索引擎为X!Tandem(v2010.10.01 .1 )[23],使用搜索引擎的默认参数并假设这些参数已经被最优化。对于18 mixtures,Sigma49和Yeast数据集,所有的二级质谱只搜索目标蛋白质数据库。对于DME,HumanMD和HumanEKC,二级质谱需要同时搜索目标和诱饵数据库。当数据库搜索引擎报告了肽段及其鉴定分数后,实验继续使用包含在TPP v4.5中的PeptideProphet[24]对鉴定结果做后续处理,得到肽段的鉴定概率。
本文将PGMPi和其他2个蛋白质推断算法MSBayesPro和Fido进行比较。这2个算法都明确地使用条件概率处理肽段退化问题而且它们的程序包是开源的。实验运行MSBayesPro和Fido算法时均使用默认参数。PGMPi是使用R语言进行实验求解的,该方法只有一个参数α,设定其取值范围为α∈[0.2,0.8],实验设置PGMPi的参数α=5。
2.3 实验结果本文通过生成曲线评估不同的蛋白质推断算法的表现。该曲线根据不同的q_value绘制正确发现的蛋白质鉴定物(TP)的个数。一个鉴定得到的蛋白质如果出现在相应的蛋白质参考集或者目标蛋白质数据库中,则认为被正确发现(TP);反之,则认为该蛋白质是错误发现的(FP)。给定某个概率阈值t,如果蛋白质概率值大于阈值t的蛋白质中有Tt个正确发现蛋白质和Ft个错误发现蛋白质,那么错误发现率(FDR)用如下方式计算:FDRt=Ft/(Tt+Ft)。相应的q_value定义为一个蛋白质被报告的最小FDR:qt=mini≤tFDRi:qt=mini≤tFDRi。然后,通过不断地改变概率阈值t生成最终的曲线。多个方法报告的排名最高的蛋白质拥有相同的分数1.0,这些蛋白质在输出文件中的排序是随机的。本文跳过这些具有相同概率的蛋白质,从下一个出现的拥有不同概率的蛋白质开始计算q_value。
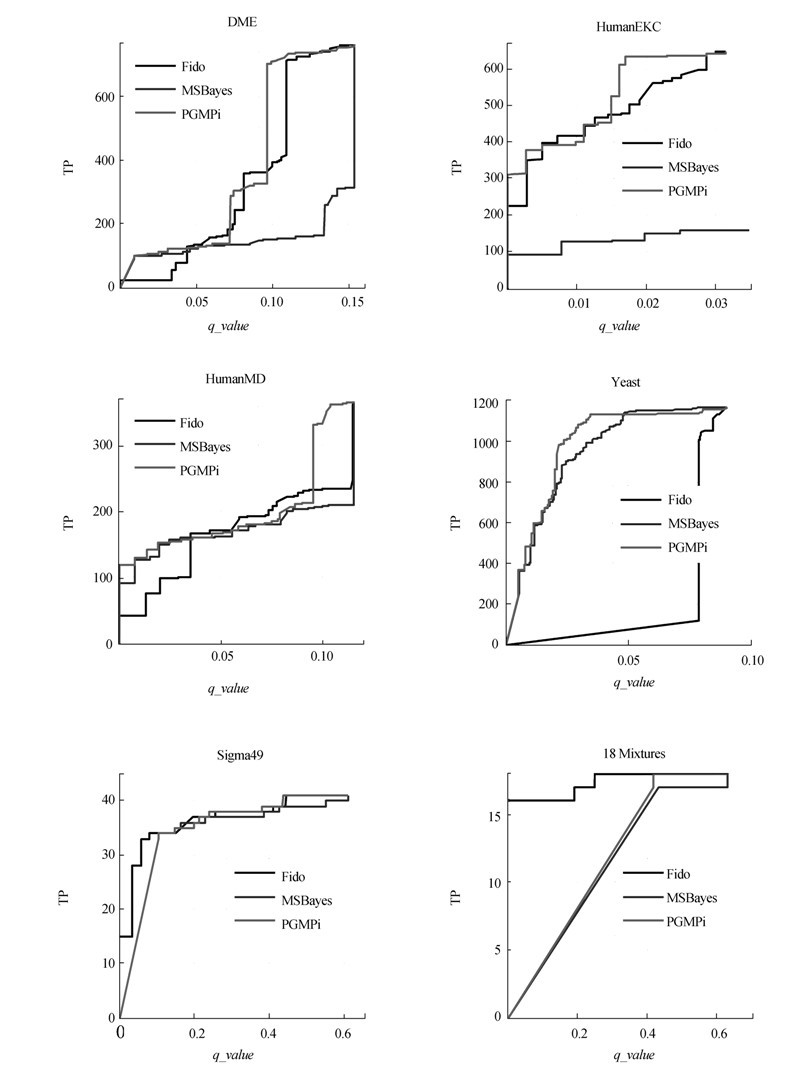
图 4所示为3种不同的蛋白质推断算法的在6个数据集上的推断结果评估曲线。一方面,这3个方法中没有一个能在所有数据集上都表现为最好。在6个数据集上,PGMPi是最稳定的并且没有最差的表现。总体来说,PGMPi在Yeast,DME,Sigma_49和HumanEKC数据集上几乎都是表现最好的(或者和其他方法的表现非常相近)。同时,PGMPi在18 mixtures数据集上表现次好。具体地说,在所有6个数据集上,PGMPi击败Fido 4次,击败MSBayesPro 5次。另一方面,当q_value等于0时(没有报告任何错误的蛋白质),PGMPi在HumanMD和HumanEKC数据集上能够报告最多的正确蛋白质。其他2个推断算法也能在某些数据集上有类似的表现但没有PGMPi多。具体的数据是:不报告任何错误的蛋白质时,Fido在一个数据集上报告最多的正确的蛋白质,而MSBayesPro在所有数据集都没有这样的表现。
|
| 图 4 3种不同蛋白质推断算法的推断结果 Fig. 4 Performance comparison among three different protein inference algorithms |
图 4绘制了3个蛋白质推断方法PGMPi、Fido和MSBayesPro在不同q_value下正确报告的蛋白质的个数。整体来说,PGMPi在6个数据集上表现比较稳定,尤其是在DME、HumanEKC及Yeast等3个数据集上都是表现最好的;在HumanMD和Sigma_49数据集上当q_value较小时,表现不是最优的,但随着q_value的增加,PGMPi较MSBayesPro和Fido而言都是最先达到最优的;18 mixtures中PGMPi是表现次优的。而Fido虽然在18 mixtures数据集中明显优于其他2个算法,但是在其他数据集中的表现都不是太理想,尤其是在Yeast数据集中的表现远远落后于其他2个算法,这也表明Fido在针对个别数据集来说可能会比较适合,模型相对来说不稳定。对于MSBayesPro,该算法在Sigma_49数据集上,当q_value较小时,相比于PGMPi和Fido有不太显著的优势,但随着q_value的增加就被PGMPi超过;在DME和HumanEKC两个数据集上MSBayesPro都显著弱于其他2个算法,表现相对较差,尤其是在HumanEKC数据集上,PGMPi和Fido都在q_value=0.03时可以全部鉴定出样品中存在的蛋白质,而对于MSBayesPro,当q_value=0.035时还是没能达到最优解,由于其效果较差,为了便于比较将q_value>0.035的部分去掉了;MSBayesPro只在Yeast以及Sigma_49这2个数据集上和表现最好的方法相比,没有明显的差异;总的来说,MSBayesPro在6个数据集中的表现相比于其他蛋白质推断方法不太稳定。
2.4 参数影响由于PGMPi只有一个参数,同MSBayesPro及Fido两个模型的对比实验是在α=0.5的情况下进行的,但其他参数对推断效果是否有明显的影响,即模型对参数是否是敏感的还未可知。所以本文对参数在各个数据集上的影响做了对比实验,以测试模型对参数的敏感度。
由于生物信息的多样性以及不确定性,导致同一模型对于相同参数在不同数据集的表现不一,同时同一模型不同参数对于结果也有着或多或少的影响。图 5报告的是PGMPi模型中不同参数在6个数据集上对于结果的影响,本文给定模型的参数取值区间为α∈[0.2,0.8],实验选取了0.2、0.3、0.5、0.7以及0.8等5个不同参数并绘制出在不同数据集上的结果对比图(如图 5 所示),可以看出该模型不同参数的设置对于结果的影响不是很明显,也就是说模型对于参数是不敏感的、相对稳定的。具体而言,在18 mixtures、Yeast以及Sigma49数据集上不同参数对于推断的结果几乎没有影响;在HumanEKC和HumanMD两个数据集上,可以看出,当参数α=0.2时,其结果相对来说较好,但整体来说相对稳定,波动不大;而对于DME数据集,参数对于其结果有着相对明显的影响,随着参数的增加,效果相对来说有些下降。总体来说,模型参数在5个数据集上表现相对稳定,而对于DME参数对于结果有着些许的影响,这是由于数据集的不同导致出现的差异,所以参数可能导致结果有些许的波动,但在可接受的范围内。因此该模型对参数是不敏感的、相对稳定的。关于参数α的取值范围,由于参数α表示的是某个候选蛋白质存在其对应的一个肽段被检测到的概率。理论上来说参数α的取值范围应为(0,1],但是实验证明当参数α=0.1时在某些数据集上就不能正确地推断蛋白质,其最后的结果中存在某些蛋白质的后验概率为无意义的数(NaN)。导致这种情况的原因,可能有2种情况:一种是由于生物样本酶解的过程产生的,酶解过程为生物过程,我们无法精确地测量,在这个过程中,蛋白质酶解的程度对于结果的预测也有着很大的影响,比如可能存在这样一种情况,就是某个蛋白质包含肽段j,但是酶解过程中将肽段水解成较小的氨基酸片段,这样就鉴定不到该肽段的存在,特别是在这个蛋白质只含有这一种肽段的情况下,就无法鉴定蛋白质的存在。另一种可能是由于数据集的不同,也就是产生数据集中候选蛋白质的生物组织的不同,蛋白质酶解所需的水解酶不一样,导致酶解效果以及酶解程度不同,对于蛋白质包含的肽段可能没有酶解出来,也可能酶解成更小的氨基酸片段。从而导致推断结果有误差,甚至出现无意义的数。综合各种情况,本文选取了一个比较合理的参数取值[0.2,0.8],实验结果表明,虽然对于参数的变化模型效果表现比较稳定,但是仍可以看出当参数α=0.2时,其推断结果会相对更好一些,也就是说候选蛋白质产生其对应的肽段的概率小于0.2,从这也侧面说明了生物酶解过程的随机性、不彻底性。

|
| 图 5 参数对于模型结果的影响 Fig. 5 The effect of the parameter on the identification performance |
蛋白质组学的一个重要目标是能够快速准确地进行蛋白质鉴定,即确定一个样本中真实存在的蛋白质,故蛋白质鉴定问题得到了许多研究人员的关注。本文将蛋白质推断问题抽象为概率图求解问题,并提出了一种基于概率图模型的方法(PGMPi)来解决蛋白质推断问题。该模型首先给出了质谱、肽段以及候选蛋白质的联合概率分布,根据给定的一些假设条件以及联合概率确定每个蛋白质的后验概率分布,从而将求解具有最大联合概率分布的候选蛋白质子集转化为寻找一个具有最大后验的蛋白质配置问题,最后采用吉布斯抽样来对模型进行求解,从而获得具有最大后验的最优蛋白质配置。实验结果表明,本文提出的PGMPi的推断表现不弱于其他蛋白质推断算法,并且同Fido和MSBayesPro相比,表现比较稳定。特别是,PGMPi只有一个参数,并且实验表明PGMPi在大多数数据集上对参数是不敏感的,不受参数设定的影响。
| [1] | ALTELAAR A F M, MUNOZ J, HECK A J R. Next-generation proteomics: towards an integrative view of proteome dynamics[J]. Nature reviews genetics, 2013, 14(1): 35-48. |
| [2] | NOBLE W S, MACCOSS M J. Computational and statistical analysis of protein mass spectrometry data[J]. PLoS comput biol, 2012, 8(1): e1002296-e1002296. |
| [3] | AEBERSOLD R, GOODLETT D R. Mass spectrometry in proteomics[J]. Chemical reviews, 2001, 101(2): 269-296. |
| [4] | PENG J, ELIAS J E, THOREEN C C, et al. Evaluation of multidimensional chromatography coupled with tandem mass spectrometry (LC/LC-MS/MS) for large-scale protein analysis: the yeast proteome[J]. Journal of proteome research, 2003, 2(1): 43-50. |
| [5] | HUNT D F, YATES J R, SHABANOWITZ J, et al. Protein sequencing by tandem mass spectrometry[J]. Proceedings of the national academy of sciences, 1986, 83(17): 6233-6237. |
| [6] | NESVIZHSKII A I, KELLER A, KOLKER E, et al. A statistical model for identifying proteins by tandem mass spectrometry[J]. Analytical chemistry, 2003, 75(17): 4646-4658. |
| [7] | SERANG O, MACCOSS M J, NOBLE W S. Efficient marginalization to compute protein posterior probabilities from shotgun mass spectrometry data[J]. Journal of proteome research, 2010, 9(10): 5346-5357. |
| [8] | SHEN C, WANG Z, SHANKAR G, et al. A hierarchical statistical model to assess the confidence of peptides and proteins inferred from tandem mass spectrometry[J]. Bioinformatics, 2008, 24(2): 202-208. |
| [9] | LI Y F, ARNOLD R J, LI Y, et al. A Bay esian approach to protein inference problem in shotgun proteomics[J]. Journal of computational biology, 2009, 16(8): 1183-1193. |
| [10] | MA Z Q, DASARI S, CHAMBERS M C, et al. IDPicker 2.0: Improved protein assembly with high discrimination peptide identification filtering[J]. Journal of proteome research, 2009, 8(8): 3872-3881. |
| [11] | CLAASSEN M. Inference and validation of protein identifications[J]. Molecular & cellular proteomics, 2012, 11(11): 1097-1104. |
| [12] | HUANG T, WANG J, YU W, et al. Protein inference: a review[J]. Briefings in bioinformatics, 2012, 13(5): 586-614. |
| [13] | LI Y F, RADIVOJAC P. Computational approaches to protein inference in shotgun proteomics[J]. BMC bioinformatics, 2012, 13: 1-17. |
| [14] | CHENG QIANG, CHEN FENG, DONG JIAN WU, et al. Variational approximate inference methods for graphical models[J]. Acta Automatica Sinica, 2012,38(11): 1721-1734(in Chinese).程强,陈峰,董建武等,概率图模型中的变分近似推理方法[J]. 自动化学报, 2012, 38(11): 1721-1734. |
| [15] | COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data[J]. Machine learning, 1992, 9(4): 309-347. |
| [16] | HASTIE T, TIBSHIRANI R, FRIEDMAN J, et al. The elements of statistical learning: data mining, inference and prediction[J]. The mathematical intelligencer, 2005, 27(2): 83-85. |
| [17] | BENJAMINI Y, HOCHBERG Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing[J]. Journal of the royal statistical society. series B (Methodological), 1995, 57(1): 289-300. |
| [18] | TABB D L, FERNANDO C G, CHAMBERS M C. MyriMatch: highly accurate tandem mass spectral peptide identification by multivariate hypergeometric analysis[J]. Journal of proteome research, 2007, 6(2): 654-661. |
| [19] | RAMAKRISHNAN S R, VOGEL C, KWON T, et al. Mining gene functional networks to improve mass-spectrometry-based protein identification[J]. Bioinformatics, 2009, 25(22): 2955-2961. |
| [20] | BRUNNER E, AHRENS C H, MOHANTY S, et al. A high-quality catalog of the Drosophila melanogaster proteome[J]. Nature biotechnology, 2007, 25(5): 576-583. |
| [21] | RAMAKRISHNAN S R, VOGEL C, PRINCE J T, et al. Integrating shotgun proteomics and mRNA expression data to improve protein identification[J]. Bioinformatics, 2009, 25(11): 1397-1403. |
| [22] | HUANG T, HE Z. A linear programming model for protein inference problem in shotgun proteomics[J]. Bioinformatics, 2012, 28(22): 2956-2962. |
| [23] | CRAIG R, BEAVIS R C. TANDEM: matching proteins with tandem mass spectra[J]. Bioinformatics, 2004, 20(9): 1466-1467. |
| [24] | KELLER A, NESVIZHSKII A I, KOLKER E, et al. Empirical statistical model to estimate the accuracy of peptide identifications made by MS/MS and database search[J]. Analytical chemistry, 2002, 74(20): 5383-5392 |



