概念格也称为Galois格,又叫做形式概念分析,由德国的Wille[1]在20世纪80年代提出。概念格的每个节点是一个形式概念,概念格结构模型是形式概念分析中的核心结构,它描述了对象和属性之间的关系。概念格是研究知识表示和推理的理论,它具有严格的数学模型,已经在机器学习、数据挖掘、软件工程等领域[2, 3, 4, 5, 6]得到广泛的应用。
通常我们研究的形式背景是完备的,也就是对象和属性之间的关系是已知的,但是在实际应用中,大多数信息是模糊[7]的、复杂的。更糟糕的是在现实生活中由于人的认知能力以及机器的局限性,人们经常不能准确地判断对象和属性之间的关系,使得获取的形式背景经常存在数据缺失,从而得到形式背景是不完备的模糊形式背景,这对于知识获取产生了很大障碍。因此不完备模糊形式背景的研究获得了广泛的关注。
粗糙集理论中的信息系统就是形式概念分析中的形式背景,对于不完备信息系统[8],粗糙集已通过相容关系、非对称相似关系等进行了一些研究。在形式概念分析中Liu J等在文献[9]中将多值形式背景转变为单值形式背景后,通过把不完备属性在不同对象上的不同取值进行扩展,从而得到了完备的形式背景来进行概念的提取。Dubois D等在文献[10]提出了利用概率论来解决不完备形式背景的方法。Krupka M等在文献[11]中定义了不完备的模糊形式背景,然后提出了在不完备模糊形式背景下构建概念格的方法。Djouadi Y等在文献[12] 中将不完备模糊形式背景中的隶属度值均采用区间值来表示,将不完备模糊形式背景转化为区间值模糊形式背景(interval -valued fuzzy formal concept,IVFF),在此基础上提出了基于区间值形式背景的概念格构建方法。Li J H等在文献[13]中提出了在不完备形式背景下构建相似概念格的方法,此外基于相似概念格还研究了在不完备的决策形式背景下获取规则的方法。上述研究中,无论是将不完备形式背景转化为区间值形式背景,还是对不完备性进行扩展来构造概念格的方法,仅仅适用于形式背景中数据量缺失较少的情况。当形式背景中数据缺失量较大时,所构造的概念格中包含有大量不确定的信息,这对知识获取造成了很大影响。
本文为了减少形式背景中数据缺失量对知识获取的影响,提出并定义了相似模糊概念和相容模糊概念并给出了相容模糊概念的构建方法,建立了相容模糊概念之间的偏序关系,进而设计面向模糊不完备信息的关联规则挖掘算法。
1 基本概念 1.1 形式概念分析
定义1[1] 一个形式背景K=(G,M,I)是一个三元组 ,其中G是对象集合,M是属性集合,I是G与M之间的一个二元关系gIm或(g,m)∈I,表示对象g具有属性m。在形式背景中定义式(1)和式(2):
\[F(A)=\{m\in M|gIm,\forall g\in A\},A\subseteq G\]
(1)
\[G(B)=\{g\in G|gIm,\forall m\in B\},B\subseteq M\]
(2)
形式背景能用一个二维表表示,如表 1,其中对象集G=x1,x2,x3,x4,属性集M=a,b,c,d 。表中1表示某对象拥有某属性,0表示某对象不拥有某属性,例如x1有a属性,没有b属性。
定义2[1] 形式背景K=G,M,I中一对二元组(A,B)称为形式概念,当且仅当F(A)=B与G(B)=A同时成立(A$ \subseteq $G,B$ \subseteq $M),其中A叫做形式概念的外延,B叫做形式概念的内涵。
假定A1,B1与A2,B2是形式背景(G,M,I)下的两个概念,这两个概念间可以建立起偏序关系A1,B1≤A2,B2⇔A1$ \subseteq $A2(⇔B2$ \subseteq $B1) 。领先次序意味着A1,B1是A2,B2的子概念。根据概念间的偏序关系生成格的Hasse图见图 1。下面是在形式背景K下生成的概念:

|
| 图 1 表 1对应概念格的Hasse图 Fig. 1 Hasse diagram of table 1 |
1){∅,(a,b,c,d)};
2){(x1),(a,d)};
3){(x3),(a,c)};
4){(x2),(b,c)};
5){(x1,x3),(a)};
6){(x2,x3,x4),(c)};
7){(x1,x2,x3,x4),∅}。
定义3[14] 一个模糊形式背景是一个三元组(G′,M′,I′),其中G′是对象的有限集,M′是属性有限集,I′是G′×M′的模糊集合。(g,m)∈I′有一个隶属度值u(g,m)∈[0, 1] 。
定义4[14] 给定一个模糊形式背景K′={G′,M′,I′=φ(G′×M′)}和一个置信度阈值T=[t1,t2],在形式背景中定义式(3)与式(4):
\[\text{FA}(A)=\{m\in M'|\forall g\in A:{{t}_{1}}\le u(g,m)\le {{t}_{2}}\}\]
(3)
\[\text{FO}(B)=\{g\in G'|\forall m\in B:{{t}_{1}}\le u(g,m)\le {{t}_{2}}\}\]
(4)
模糊形式背景(G′,M′,I′)同置信度阈值T下的一个二元组(A,B)(A$ \subseteq $G′,B$ \subseteq $M′)是模糊形式概念,当且仅当FA(A)=B与FO(B)=A同时成立。A、B分别叫做模糊形式背景的模糊外延和模糊内涵。
定义5[14] (A1,B1)和(A2,B2)是形式背景(G′,M′,I′)的两个模糊概念。(A1,B1)是(A2,B2)的子概念,记作(A1,B1)≤(A2,B2),当且仅当A1$ \subseteq $A2(⇔B2$ \subseteq $B1)。
目前所研究的形式背景是完备的,换句话讲,此时对象或者具有某属性,或者不具有某属性,他们之间的关系是确定的。数据缺失现象在生活中普遍存在。例如,对一些突发事件,并没有该事件的完整记录;再如病人突发疾病,而不能对病人进行全面检查,然后来制定相应的治疗方案。下面给出一个例子来说明,表 2是医生诊断表,即为不完备模糊形式背景,其中o1、o2、o3、o4表示病人编号,组成对象集G′。a、b、c、d、e、f表示病人的症状,其代表为头痛、血压、恶心、食欲不振、咳嗽、乏力,组成属性集M′。用*来表示缺失数据,但是这些数据是客观存在的。
| a | b | c | d | e | f | |
| o1 | 0.8 | 0.1 | 0.61 | 0.6 | 0.8 | * |
| o2 | 0.9 | 0.85 | * | 0.2 | 0.7 | 0.9 |
| o3 | 0.21 | * | 0.87 | * | 0.6 | 0.6 |
| o4 | 0.6 | * | 0.30 | * | 0.5 | 0 |
一个置信度阈值T设置在区间[t1,t2]中。通过设置置信度阈值可以消除一些不在这个值之内的关系,对于t1与t2的值用户可以根据需要来设定。例如在表 2中设定模糊形式背景的置信度阈值为T=0.5,1,对于表中(o1,b)的隶属度值为0.1,认为病人o1的血压没有问题,可以不考虑。
2 相似模糊概念与相容模糊概念在形式概念分析中,对不完备形式背景进行完备化处理,一般可采用以下3种方法。
1)删除法。删除法即删除形式背景中缺失数据的一列或者一行,也就是删除一个对象或者删除一个属性。这类方法操作起来比较简单,但是在删除过程中会导致原先存在的数据缺失,可能会造成获取的知识不准确。
2)填补法。填补法就是对不完备形式背景中缺失的数据填充为1或者0,使之补全为一个完备的形式背景。这类方法比较简单,但是容易造成获取的知识错误,因为好多缺失信息都是人为地填充0或者1。
3)扩展属性法[15]。扩展属性法即把原有不完备形式背景下的属性集合中的属性分为完备和不完备属性两部分,然后将不完备属性在不同对象的不同取值进行扩展,从而把不完备形式背景补充完整。此方法的好处是既不会增加知识也不会缺失知识,但是增加了知识获取的时间和空间复杂度。
定义6 在不完备模糊形式背景Kc=(G′,M′,IM) 中,对于集合A∈G′,记作:
\[\begin{align}
& \underline{FA(A)}=\{m\in M'|\forall g\in A:{{t}_{1}}\le \\
& u(g,m)\le {{t}_{2}}或u(g,m)=*\} \\
\end{align}\]
(5)
\[\begin{align}
& \underline{FO(B)}=\{g\in G'|\forall m\in B:{{t}_{1}}\le \\
& u(g,m)\le {{t}_{2}}或u(g,m)=*\} \\
\end{align}\]
(6)
如果\[\underline{FA(A)}\]=B且\[\underline{FO(B)}\]=A称(A,B)为模糊形式背景Kc下的一个相似模糊概念,g∈A时ug为A,B中对象g的隶属度值,其表示如式(7):
\[{{u}_{g}}=\min (u(g,m))m\in B\]
(7)
特别地当u(g,m)=*时可用补全法补全g与m的隶属度值。在不完备形式背景下所有相似模糊概念构成的集合可表示为wKc。
在相似概念A,B中,如果含有大量缺失数据,则涉及A,B的任何应用都是不可靠的,即它不仅降低了知识获取的有效性,反而会使不确定性进一步扩散。下面在相似模糊概念的基础上提出了相容模糊概念,通过设置参数(α,β)可满足不同用户的需求,(α,β)就叫做相容参数。
定义7 在不完备模糊形式背景Kc=G′,M′,IM中,设A$ \subseteq $G′,B$ \subseteq $M′,A,B∈wKc,
0≤α,β≤1,记作:
\[\chi (A,B)=\{a\in B|\left| A,B{{)}_{a}} \right|\ge \alpha \times \left| A \right|\}\]
(8)
\[\varphi (A,B)=\{x\in A|\left| A,B{{)}^{x}} \right|\ge \alpha \times \left| B \right|\}\]
(9)
\[\gamma (A,B)=\frac{1}{|A|+|B|}(|\chi (A,B)\left| + \right|\varphi (A,B)|)\]
(10)
如果γ(A,B)≥β则称(A,B)是相容模糊概念,定义u为(A,B)的隶属度值,u可以表示为
\[\bar{u}=\frac{\sum\limits_{g\in A}{{{u}_{g}}}}{|A|}\]
(11)
在不完备模糊形式背景Kc中,基于参数(α,β)的所有相容概念构成的集合为wβα(Kc)。不完备模糊形式背景Kc用补全法转化为完备的模糊形式背景,其上获得的相似模糊概念wKc中有许多填充的信息,通过参数α与外延中对象数量与内涵中属性数量的乘积,即α×A与α×B可以去掉填充值较大概念。
定义8 如果在一个相容模糊概念中有u(g,m)=*则这个相容模糊概念称为粗糙概念,反之称为精确概念。
定理1 在不完备模糊形式背景Kc=G′,M′,IM中,如果(A,B)是粗糙概念,那么这个相容模糊概念的子概念至少存在一个概念,其粗糙度为
\[\frac{|u{{(g,m)}_{(\forall g\in A)}}=*|}{|A|\times |B|}\]
(12)
证明 假设(A1,B1)是(A,B)的一个子概念,(A,B)是粗糙相容模糊概念,即存在u(g,m)=*,根据概念之间的继承关系可知g∈A1,m∈B1。
相似模糊概念与相容模糊概念既有区别也有联系,在经典的不完备形式背景中“补全法”将缺失数据补充为1,而在不完备的模糊形式背景中,相似模糊概念是将不完备模糊形式背景中的缺失数据补充为0.5得到的。而相容模糊概念是对相似模糊概念的扩展,它是在相似模糊概念基础上通过设置参数(α,β),去除一些数据量缺失较大的相似模糊概念而得到的。根据定义6和定义7以及传统的概念获取算法[16],可以得出相似模糊概念和相容模糊概念的构造算法,具体算法步骤参考算法1与算法2。
算法1 在不完备形式背景Kc中,相似模糊概念的构造算法。
输入 不完备模糊形式背景Kc=G′,M′,IM,wKc为空集。
输出 相似模糊概念w(Kc)。
1)先对不完备模糊形式背景进行处理,如果u(g,m)小于置信度阈值T,则u(g,m)为0,然后将Kc中的空缺数据*全部填充为0.5,即用补全法把不完备形式背景转化为完备形式背景。
2)获得第一个概念(FO(M),M)设置概念的隶属度值并加入w(Kc)中。
3)遍历对象g,其中g∈G,如果遍历完成转到6),反之转到4)。
4)遍历近似模糊概念(A,B),其中(A,B)∈wKc,如果遍历完成转到3),否则转到5)。
5)求出B与FA(g)交集I,如果获得的交集I不是已获得w(Kc)的内涵,则计算出(FO(I),I)隶属度值并加入w(Kc)中然后回到4)。
6)输出w(Kc),算法结束。
算法2 在不完备形式背景Kc中,相容模糊概念的获取算法。
输入 不完备模糊形式背景Kc=(G′,M′,IM),相似模糊概念w(Kc),wβα(Kc)为空集。
输出 相容模糊概念w(βα(Kc)。
1)任取wKc里的相似模糊概念并计算出χ(A,B)、φ(A,B)与γ(A,B)。如果γ(A,B)>β,计算出(A,B)的隶属度值u并加入到相容模糊概念wβα(Kc)中。
2)如果相似模糊概念都被进行计算过,则输出相容模糊概念转到3),反之再进行1)。
3)输出wβα(Kc),算法结束。
3 基于相容模糊概念的规则提取关联规则数据挖掘中最活跃的研究方法之一[17, 18, 19, 20, 21]。规则就是形如“如果…那么…(If…Then…)”前者为条件,后者为结果。典型的关联规则发现问题是对超市中的购物篮数据进行分析,例如最著名的案例就是啤酒与尿布。
对于关联规则A⇒B的支持度是supp(A⇒B)=|FO(A∪B)|/|U|,置信度为conf(A⇒B)>β关联规则A⇒B被称为关于(ω,τ)关联规则,当supp(A⇒B)>ω时把A∪B称为频繁的。
在不完备的模糊背景下,规则提取是一件比较困难的工作,在之前的工作中已经获得了相似模糊概念和相容模糊概念,然后根据算法3构造好相似模糊概念格,但是由于相似模糊概念中有许多不确定性信息,所以构造的相似模糊概念格也是不准确的。通过对相似模糊概念的筛选,最后得到了较为准确的相容模糊概念,可以在构造好的相似模糊概念格基础上得到相容模糊概念的之间的偏序关系,从而可以提取出可信度较高的关联规则,具体算法参考算法4。
算法3 相似模糊概念格的构造算法。
输入 不完备模糊形式背景Kc=(G′,M′,IM),相似模糊概念w(Kc)。
输出 相似模糊概念格。
1)遍历相似模糊概念(A,B),其中(A,B)∈w(Kc),并且设置(A,B)的count为0。如果遍历完成则转4),否则转2)。
2)遍历属性m,其中m∈M,并求得A与FO(m)交集I。如果遍历结束转到1),否则转到3)。
3)在wKc找出相似模糊概念A1,B1使得A1=I,并把概念A1,B1的 count值加1。假如|B1|-|B|等于A1,B1的count值,则增加边在A1,B1与(A,B),反之转2)。
4)输出相似模糊概念格,算法结束。
算法4 不完备形式背景下规则提取的算法。
输入 不完备模糊形式背景Kc=G′,M′,IM,相容模糊概念wβα(Kc)。
输出 关联规则∑。
1)对相似模糊概念格进行处理,除去相容模糊概念之外的概念,更新父节点和子节点。
2)如果概念C1=A1,B1与C2=A2,B2满足C2是C1的父节点,且满足C1与C2的隶属度大于给定的阈值η,即$\frac{\min (\bar{u}({{A}_{1}},{{B}_{1}}),\bar{u}({{A}_{2}},{{B}_{2}}))}{\max (\bar{u}({{A}_{1}},{{B}_{1}}),\bar{u}({{A}_{2}},{{B}_{2}}))}>\eta $,则可以将得到的规则B2=B1-B2加入∑中,其可信度是|A1|/|A2|。
3)如果对于节点C=A,B有多个双亲节点,则任取两个双亲节点C1=A1,B1与C2=A2,B2,如果满足条件$\frac{\min (\bar{u}({{A}_{1}},{{B}_{1}}),\bar{u}({{A}_{2}},{{B}_{2}}))}{\max (\bar{u}({{A}_{1}},{{B}_{1}}),\bar{u}({{A}_{2}},{{B}_{2}}))}>\eta $,则可以提取到的规则B1⇒B2与B2⇒B1,并将其加入∑中,支持度分别为|A|/|A1|与|A|/|A2|。
4)输出∑。
在得到提取规则∑后,可以给其支持度阈值ω与置信度阈值τ。然后根据需要从提取的规则中筛选出符合要求的规则。
4 示例展示现在举例来展示规则提取的过程,在表 3中讨论的置信度阈值是T=[0.5,1],通过算法1,可以得出在表 3的不完备模糊背景下形成的相似模糊概念为
| a | b | c | d | e | f | |
| o1 | 0.8 | 0 | 0.61 | 0.6 | 0.8 | * |
| o2 | 0.9 | 0.85 | * | 0 | 0.7 | 0.9 |
| o3 | 0 | * | 0.87 | * | 0.6 | 0.6 |
| o4 | 0.6 | * | 0 | * | 0.5 | 0 |
1){⇒,(a,b,c,d,e,f)};
2){(0.6/o1),(a,c,d,e,f)};
3){(0.5/o2),(a,b,c,e,f)};
4){(0.61/o1,0.5/o2),(a,c,e,f)};
5){(0.5/o3),(b,c,d,e,f)};
6){(0.6/o1,0.5/o3),(c,d,e,f)};
7){(0.5/o2,0.5/o3),(b,c,e,f)};
8){(0.61/o1,0.5/o2,0.6/o3),(c,e,f)}.;
9){(0.5/o4),(a,b,d,e)};
10){(0.6/o1,0.5/o4),(a,d,e)};
11){(0.7/o2,0.5/o4),(a,b,e)};
12){(0.8/o1,0.7/o2,0.5/o4),(a,e)};
13){(0.5/o3,0.5/o4),(b,d,e)};
14){(0.6/o1,0.5/o3,0.5/o4),(d,e)};
15){(0.7/o2,0.5/o3,0.5/o4),(b,e)};
16){(o1,o2,o3,o4),(0/a,0/b,0/c,0/d,0.5/e,0/f)}。
图 2是相似模糊概念格对应的Hasse图。上述已经得出不完备形式背景下(表 3)的相似模糊概念,然后在此基础上根据算法3构建出相似模糊概念格,通过设置相容参数(α=0.6,β=0.8)来获得所需要的可靠的相容模糊概念w0.80.6(Kc):

|
| 图 2 相似模糊概念的相似模糊概念格 Fig. 2 Approximat fuzzy concept lattice |
1){0.6/(o1),(a,c,d,e,f)};
2){0.5/(o2),(a,b,c,e,f)};
3){0.57/(o1,o2,o3),(c,e,f)};
4){0.55/(o1,o4),(a,d,e)};
5){0.6/(o2,o4),(a,d,e)};
6){0.667/(o1,o2,o4),(a,e)};
7){0.083/(o1,o2,o3,o4),(c)}。
根据算法4可以得出阈值τ为0.9,置信度阈值为0.5的关联规则:
1){a,d,e}⇒{c,f}置信度为0.5。
解释:如果头疼、食欲不振、咳嗽则恶心、乏力。
2){a,e}⇒{b}置信度为0.67。
解释:如果头疼、咳嗽则血压会高。
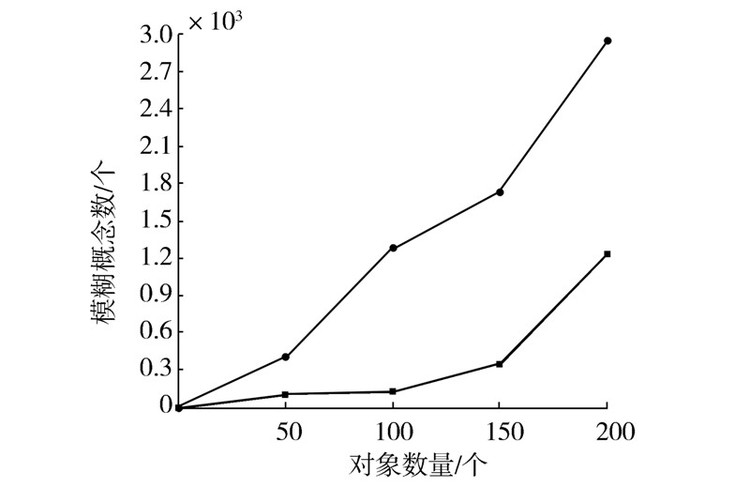
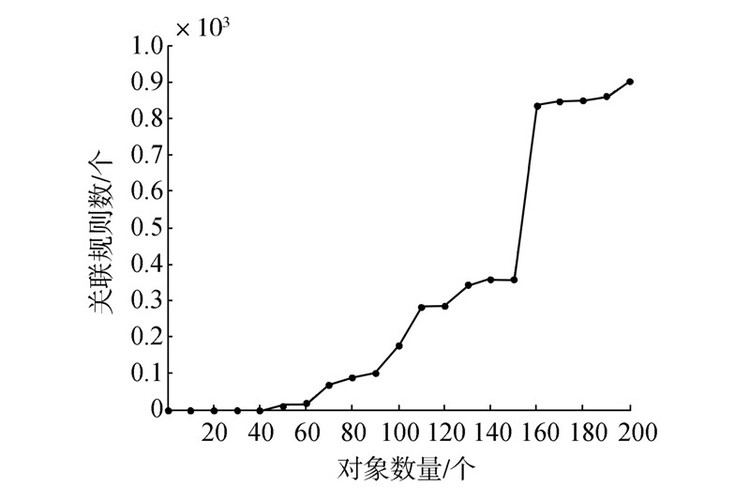
5 实验结果与分析本文基于相容模糊概念的关联规则提取可分为在不完备模糊形式背景中相容模糊概念的构造过程和根据相容模糊概念的偏序关系进行提取规则的过程。本文算法在Win7环境下用MATLAB来实现,并在UCI数据库的water数据集(526个对象,38个属性)进行实验。实验主要对2个指标进行测量:第1个是在不完备模糊形式背景下相似模糊概念数目与对象数目以及相容模糊概念与对象数目之间的关系;第2个是提取的关联规则数目与对象数目之间的关系。在本实验中针对不完备模糊形式背景,设定相容模糊参数为(α=0.8,β=0.9),关联规则的置信度阈值为0.8。在不完备形式背景下相似模糊概念与相容模糊概念的数量关系可由图 3体现,图 4则体现了对象数目与关联规则数量之间的关系。图 3与图 4都在相容模糊参数与属性数量都不变的情况下,取water数据集中的前200个对象进行测量。图 3与图 4中横坐标都表示对象的数量,初始为0,分别一次递增50与10进行测试。图 3纵坐标表示由不完备形式背景形成概念的数量,图 4纵坐标表示由相容模糊概念获得的关联规则的数量。通过图 3、4的实验结果可以观察到,在不完备模糊形式背景中随着对象数目的增多,通过本算法获得知识准确性与传统的方法相比具有一定的优势。
|
| 图 3 对象与概念个数关系 Fig. 3 Relationship between object and concept |
|
| 图 4 对象与关联规则个数关系 Fig. 4 Relationship between object and association rule |
目前在不完备模糊形式背景下的研究越来越多。本文结合在传统的不完备形式背景下获取概念的方法,提出了在不完备模糊形式背景中提取出相容模糊概念,并根据相似模糊概念格提取出相容规则的方法。实验表明,该方法可以有效的降低形式背景中因数据缺失和数据的模糊性对获取知识准确性带来的的影响。未来的工作还需要改进和细化文中的一些算法,例如如何在知识库分类能力保持不变的情况下删除不相关的冗余属性;如何把模糊概念格与粗糙集理论有效结合以解决不确定规则提取中的规则冗余性等问题。
| [1] | WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts[M]//RIVAL I. Ordered sets. Netherlands: Springer, 1982: 445-470. |
| [2] | POELMANS J, IGNATOV D I, KUZNETSOV S O, et al. Formal concept analysis in knowledge processing: a survey on applications[J]. Expert systems with applications, 2013, 40(16): 6538-6560. |
| [3] | MINEAU G W, GODIN R. Automatic structuring of knowledge bases by conceptual clustering[J]. IEEE transactions on knowledge and data engineering, 1995, 7(5): 824-829. |
| [4] | COLE R, EKLUND P W. Scalability in formal concept analysis[J]. Computational intelligence, 1999, 15(1): 11-27. |
| [5] | CARPINETO C, ROMANO G. A lattice conceptual clustering system and its application to browsing retrieval[J]. Machine learning, 1996, 24(2): 95-122. |
| [6] | MA Jianmin, ZHANG Wenxiu. Axiomatic characterizations of dual concept lattices[J]. International journal of approximate reasoning, 2013, 54(5): 690-697. |
| [7] | 胡明涵, 张莉, 任飞亮. 模糊形式概念分析与模糊概念格[J]. 东北大学学报:自然科学版, 2007, 28(9): 1274-1277. HU Minghan, ZHANG Li, REN Feiliang. Fuzzy formal concept analysis and fuzzy concept lattices[J]. Journal of northeastern university : natural science, 2007, 28(9): 1274-1277. |
| [8] | GRZYMALA-BUSSE J W. Rough set approach to incomplete data[C]//Proceedings of the 7th international conference on artificial intelligence and soft computing-ICAISC 2004. Berlin Heidelberg, Germany, 2004: 50-55. |
| [9] | LIU Jun, YAO Xiaoqiu. Formal concept analysis of incomplete information system[C]//Proceedings of the 7th international conference on fuzzy systems and knowledge discovery. Yantai, China, 2010, 5: 2016-2020. |
| [10] | DJOUADI Y, DUBOIS D, PRADE H. Possibility theory and formal concept analysis: Context decomposition and uncertainty handling[C]//Proceedings of the 13th international conference on information processing and management of uncertainty. Berlin Heidelberg, Germany, 2010: 260-269. |
| [11] | KRUPKA M. Fuzzy concept lattices with incomplete knowledge[C]//Proceedings of the 14th international conference on information processing and management of uncertainty in knowledge-based systems. Berlin Heidelberg, Germany, 2012: 171-180. |
| [12] | DJOUADI Y, PRADE H. Interval-valued fuzzy formal concept analysis[C]//Proceedings of the 18th international symposium. Berlin Heidelberg, Germany, 2009: 592-601. |
| [13] | LI Jinhai, MEI Changlin, LV Yuejin. Incomplete decision contexts: approximate concept construction, rule acquisition and knowledge reduction[J]. International journal of approximate reasoning, 2013, 54(1): 149-165. |
| [14] | LAI Hongliang, ZHANG Dexue. Concept lattices of fuzzy contexts: formal concept analysis vs. rough set theory[J]. International journal of approximate reasoning, 2009, 50(5): 695-707. |
| [15] | 何淑贤, 王育红, 翟岩慧, 等. 不完备形式背景及其完备化方法[J]. 山西大学学报:自然科学版, 2006, 29(4): 364-367. HE Shuxian, WANG Yuhong, ZHAI Yanhui, et al. Incomplete formal context and the completion approach[J]. Journal of Shanxi university : natural science edition, 2006, 29(4): 364-367. |
| [16] | 谢志鹏, 刘宗田. 概念格的快速渐进式构造算法[J]. 计算机学报, 2002, 25(5): 490-496. XIE Zhipeng, LIU Zongtian. A fast incremental algorithm for building concept lattice[J]. Chinese journal of computers, 2002, 25(5): 490-496. |
| [17] | 梁吉业, 王俊红. 基于概念格的规则产生集挖掘算法[J]. 计算机研究与发展, 2004, 41(8): 1339-1344. LIANG Jiye, WANG Junhong. An algorithm for extracting rule-generating sets based on concept lattice[J]. Journal of computer research and development, 2004, 41(8): 1339-1344. |
| [18] | LEKHA A, SRIKRISHNA C V, VINOD V. Fuzzy association rule mining[J]. Journal of computer science, 2015, 11(1): 71-74. |
| [19] | LAKHAL L, STUMME G. Efficient mining of association rules based on formal concept analysis[M]//GANTER B, STUMME G, WILLE R. Formal concept analysis. Berlin Heidelberg: Springer-Verlag, 2005: 180-195. |
| [20] | KUMAR CH A, DIAS S M, VIEIRA N J. Knowledge reduction in formal contexts using non-negative matrix factorization[J]. Mathematics and computers in simulation, 2015, 109: 46-63. |
| [21] | 王志海, 胡可云, 胡学纲, 等. 概念格上规则提取的一般算法与渐进式算法[J]. 计算机学报, 1991, 22(1): 66-70. WANG Zhihai, HU Keyun, HU Xuegang, et al. General and incremental algorithms of rule extraction based on concept lattice[J]. Chinese journal of computers, 1991, 22(1): 66-70. |



