2. 安徽大学 信息保障技术协同创新中心, 安徽 合肥 230601
2. Center of Information Support and Assurance Technology, Anhui University, Hefei 230601, China
在信息化技术迅猛发展的今天,社会网络在工作生活中发挥着越来越重要的作用。网络中的信息交流、资源交换已成为社会生活中不可缺少的重要途径。随着参与社会网络的个体增加,社会网络对于人们的重要性也随之增加,使得对社会网络的研究具有更深远的意义。近年来,对于社会网络的性质分析,逐渐从对网络整体结构分析,如发现网络的拓扑性质含有无标度、小世界特性和社团结构等,转移到对网络中重要节点的分析,如结构洞[1]、意见领袖[2]等。结构洞是网络中普遍存在的现象,在网络中占据何种位置能够获益的想法已经得到了许多人的关注。个体或者团体中的中间人可以获得丰富的信息并控制他们的网络关系,在网络中占据中心位置的主体可以获得丰厚的利益[1]。结构洞在获取网络有效信息方面起着关键的作用,且发现网络中的结构洞可以对网络结构进行优化和增强鲁棒性。结构洞理论作为网络结构分析的重要方法,在不同领域和学科的研究中都获得了丰富的成果[3, 4, 5, 6, 7]。
在结构洞研究的推进过程中,研究者发现结构洞占据者在网络中可以获得竞争优势和网络收益,并提出不同的结构洞模型。Kleinberg等[8]从战略和动态方面研究了结构洞理论,进一步扩充了伯特等研究者的工作。他们模拟了这样的过程,即当所有个体都在竞争桥节点位置的时候,社会网络随着时间是如何改变的。Buskens和Van[9]使用博弈论方法来模拟具有结构洞的网络形成过程,认为节点A只有处在节点B和C中间时才能获益。Goyal和Vega[10]提出网络形成的模型来研究社会网络中结构洞的形成,并认为当节点A位于任意长的B-C路径上,且作为节点B和C的中介时,都将获得潜在利益。这种模型将导致形成星形网络,然而,现实中的大部分网络并不一定是星形拓扑结构。Bruggeman等[11]考虑了生态位重叠导致的分散竞争对网络中个体的结构自主性的影响,修正了伯特的模型。
研究者通过对结构洞的性质进行分析,提出许多基于网络结构和社团结构的结构洞度量指标。基于网络结构的度量主要考虑结构洞的优势,伯特提出了4个定量描述结构洞的度量指标[1, 12, 13],即网络约束系数、网络有效规模、效率和等级度;Freeman提出介数中心性指标[14];Newman等[15]提出局部聚类系数;邓世果等[16]提出一种基于基尼系数的结构洞测量方法,并讨论贡献度和结构洞程度之间的关系;基于社团结构的度量主要考虑结构洞跨越不同社团的属性,Rezvani等[17]根据伯特定义中个体连接的社团数和个体的邻居节点数提出一种结构洞度量指标。
随着对结构洞的价值和意义继续深入研究,研究者提出多种结构洞发现算法,在不同结构和类型的复杂网络中准确发现结构洞占据者。Zhang等[18]认为网络中很难存在单节点形成的结构洞,他们在结构洞理论的基础上提出“广义结构洞”概念,并给出基于谱图理论的启发式“广义结构洞”发现算法DGSH。Hu等[19]将结构洞理论扩展到有向模糊社交网络并提出单向模糊结构洞和双向模糊结构洞的算法,分别计算行动者占据的单向和双向模糊结构洞个数。Lou和Tang[20]在假设网络社团结构已知的情况下,基于两级信息流理论和最小割分别提出两个结构洞占据者的挖掘算法HIS和MaxD。
目前对于结构洞[21, 22]的研究中,研究者发现社团结构与结构洞的属性存在很大关系,并提出相应算法。如Lou和Tang[20]假设社团结构已知的情况下,提出两个结构洞挖掘算法HIS和MaxD。研究者主要考虑单一粒度下的结构洞,然而网络的社团结构在不同粒度下的划分具有很大差异,且层次结构[23]具有嵌套关系。社团划分粒度由粗到细时,社团结构的规模和数量也随之变化,在粗粒度下的某个社团,粒度变细时可能划分为多个社团。如中国的行政区划,将全国看作一个大网络,可从省、市、县、乡等不同大小的区域描述网络。省、市、县、乡等分别代表不同粒度下划分的社团,从不同粒度描述,则网络社团结构也会不同。网络的层次结构特性对节点属性如重要性、中心性等具有重要影响。细粒度下的结构洞占据者在粗粒度下可能不再跨越结构洞,或结构洞程度降低甚至丧失。
综上所述,本文在单粒度基础上,研究多粒度对网络中结构洞占据者跨越结构洞程度的影响。本文提出一种基于社团结构的多粒度结构洞发现方法MG_MaxD,首先使用分层社团划分算法得到不同粒度下的社团结构;然后用结构洞发现方法获得不同粒度下的结构洞占据者集合;最后,对结构洞占据者的跨越结构洞程度的变化规律进行分析,发现结构洞占据者的结构洞程度即结构洞节点在社团间的优势会随着粒度的变细而增大。本文使用不同数据集,并进行多组对比实验,验证实验结果。
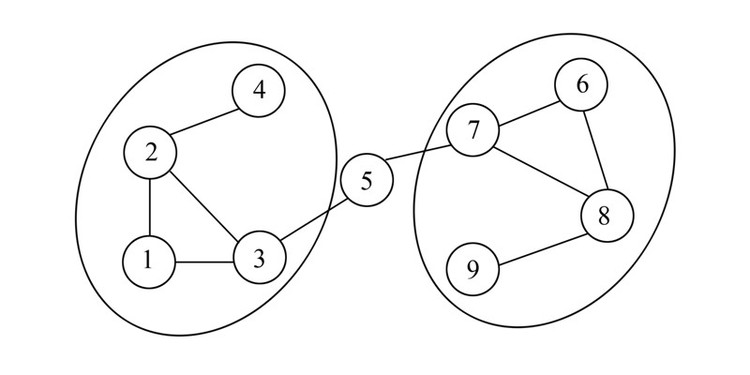
1 结构洞理论及相关算法 1.1 结构洞理论结构洞理论由美国社会学家罗纳德·博特于1992年在其撰写的《结构洞:竞争的社会结构》[1]一书中首次提出的。所谓结构洞,即“社交网络中某个或某些个体和有些个体发生直接联系,但与其他个体不发生直接联系。无直接或关系间断的现象,从网络整体看好像网络结构中出现了洞穴。”简单地说,结构洞是指两个关系人之间的非重复关系。由于社交网络中存在着不直接或间接连接的关系,从而使拥有互补资源或信息的个体之间出现了空位,也可看做网络中的洞穴。结构洞是信息流动的缺口,跨越结构洞的个体可以获得不同个体之间存在的异质性信息。如图 1所示,网络由9个节点构成,除了节点5以外,其他节点被分为两个社团,而这两个社团内的节点只能通过节点5产生联系,若没有节点5,则两侧社团之间就产生了间隙,形成了结构洞。显然,节点5占据了结构洞的位置。因此,可以通过找到类似节点5的结构洞占据者,获得网络中的异质性信息和资源。
|
| 图 1 结构洞示例 Fig. 1 Illustration of structural holes |
无权网络可以表示为G=(V,E),含有n个节点,m条边。其中V表示网络中节点的集合,E表示网络中边的集合。V={v1,v2,…,vn},E={e1,e2,…,em},社团结构为C={C1,C2,…,Cl}。
Lou和Tang[20]认为跨越结构洞的个体在不同社团间的信息传播中发挥重要作用,结构洞占据者在社团间起到桥接作用,去除这些结构洞节点后,社团间的联系将会最小化,他们根据这个思想并使用最小割提出结构洞发现方法MaxD。结合最小割定义,他们提出在去除结构洞结点后,网络G中C的最小割将显著减小,即最小割的减少量在删除结点后将会最大,目标函数如式(1)所示:
\[Q({{V}_{SH}},C)=MC(G,C)-MC(G\backslash {{V}_{SH}},C),|{{V}_{SH}}|=k\]
(1)
算法1 MaxD
输入 网络G=(V,E),结构洞个数k,社团数l,社团结构C={Ci}。
输出 Top k个结构洞占据者集合VSH。
1)初始化VSH为空集;
2)当|VSH|<k时,循环给每个节点v∈V初始化流量f(v)=0;
对每个非空S{1,2,…,l},利用源点ES=∪i∈SCi和汇点ET=∪i∉SCi在诱导后的图G\V SH上计算最大流;
对每个节点v∈V添加通过其的流f(v);
3) 选O(k)个具有最大f值的节点作候选者D;
4) 计算p*=argminp∈DMC(G\(VSH∪{p}),C);
5) 更新VSH=VSH∪{p*}
MaxD算法的输入为网络G=(V,E)和社团结构C={Ci},依据社团结构并结合最小割理论,最后得到结构洞解集VSH。但现实网络中的社团结构存在多粒度,本文主要研究多粒度对结构洞占据者跨越结构洞程度的影响。
1.3 社团划分算法
本文所使用的社团划分方法为Shen等[24]提出的能够同时探测出社团层次性和重叠性的算法EAGLE。通过凝聚的方法划分社团,研究对象为网络中的极大团,通过极大团之间的不断凝聚来实现社团划分。EAGLE算法分为2个步骤:1) 生成网络的树状图;2) 在生成树上选择合适位置断开,得到相应的社团划分。为了评判社团划分结果的质量,该算法提出一种新的模块度指标如式(2)所示:
\[EQ=\frac{1}{2m}\sum\limits_{i}{\sum\limits_{\upsilon \in C,w\in C}{\frac{1}{{{O}_{\upsilon }}{{O}_{w}}}}}\left[ \begin{matrix}
{{A}_{\upsilon w}} & -\frac{{{k}_{\upsilon }}{{k}_{w}}}{2m} \\
\end{matrix} \right]\]
(2)
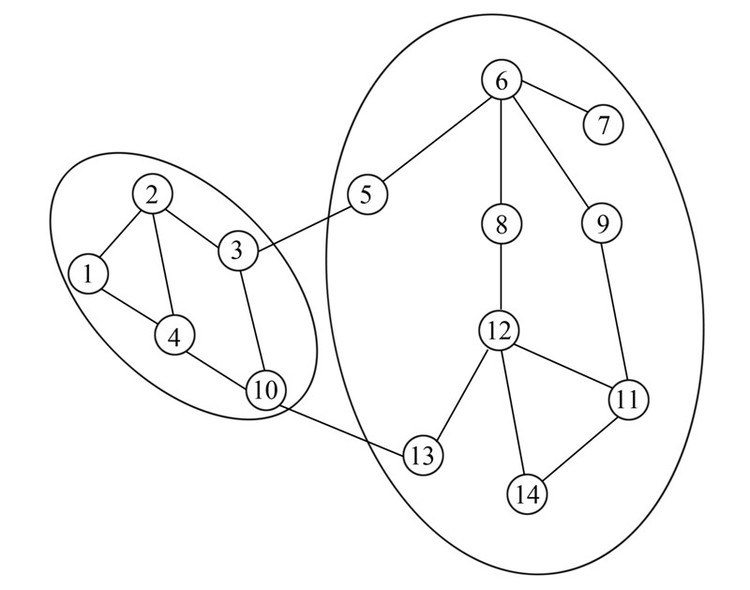
|
| 图 2 粗粒度下的社团结构 Fig. 2 Community structure in rough granularity |
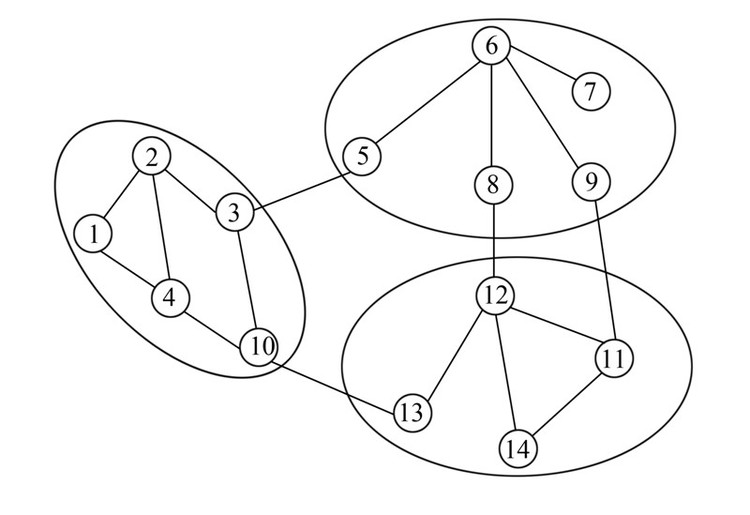
|
| 图 3 细粒度下的社团结构 Fig. 3 Community structure in fine granularity |
本文算法基于社团结构,主要思想为将多粒度[25, 26]与社团划分结合,得到不同粒度下的社团结构,最后再根据不同粒度下的社团结构求出网络中的结构洞占据者。为有效挖掘层次网络中的结构洞,我们将MaxD模型[20]中的最小割思想引入到层次网络中,作为分层网络结构洞挖掘的理论依据。在不同粒度的社团结构中,使用最大流算法,分析节点的最大流变化情况并根据最小割求出结构洞占据者。多粒度结构洞发现方法MG_MaxD的主要步骤:1)使用分层社团发现算法对网络进行多粒度划分,并得到不同粒度的社团划分结果;2)根据当前层网络的社团结构,使用MaxD算法中的最大流和最小割求出结构洞占据者;3)重复第2)步,直到求出前r层的结构洞占据者集合VrSH。实验最后将分析不同粒度下结构洞占据者的结构洞程度变化。MG_MaxD算法的输入为网络G、结构洞个数k、分层数r;输出为前r层结构洞占据者集合VSHr。MG_MaxD算法具体步骤如下。
算法2 层次结构网络结构洞发现方法MG_MaxD
输入 网络G=(V,E),结构洞个数k,分层数r
输出 前r层结构洞占据者集合VrSH
1)使用分层社团发现算法将网络G分层,并获得前r层的网络社团结构C={Cih}(1≤h≤r,1≤i≤nh},式中Cih表示第h层的第i个社团,nh表示第h层的社团个数,h越大,表示社团划分粒度越细。
2) 对Ch(1≤h≤r)层网络
给每个节点v∈V初始化流量f(v)=0;
对每个非空Sh{1,2,…,l},l为当前层网络社团个数;
利用源点ES=∪i∈ShCih和汇点ET=∪i∉ShCih,在图G\VhSH上计算最大流;
对每个节点v∈V,对节点v添加通过其的流f(v)。
3) 选择O(k)个具有最大f值的节点作为候选者D。
4) 对ph∈D,即第h层网络的结构洞占据者候选节点,计算:ph*=argminph∈DMC(G\(VSHh∪{ph}),Ch)。
5) 更新VSHh=VSHh∪{ph*}。
6) 重复2) ~ 5),直到|VhSH|=k。
7) 重复2) ~ 6),直到求出前r层的结构洞占据者集合VSHr。
社团结构是复杂网络最重要和最普遍的拓扑性质之一。在信息传播网中,同一社团内的信息传播较为迅速,而社团间的信息传播较为缓慢。在分层网络中,社团划分粒度的变化将改变整个网络的社团结构,跨越社团的结构洞占据者属性也会随之变化。对分层网络中的结构洞占据者进行发现及分析可以帮助揭露多粒度网络中节点跨越结构洞程度,即不同粒度下结构洞节点在社团间信息传播和异质性资源获取方面优势的变化,以及结构洞位置的变化情况。
在MG_MaxD方法中,使用EAGLE算法首先获得最优模块度下的社团结构,然后在此社团结构下,将网络细化得到较细粒度下的社团结构,重复此步骤直到获得前r层的社团结构。根据获得的多粒度社团结构,使用MG_MaxD算法获得网络G在不同粒度下的前k个结构洞占据者。社团划分粒度越细,则网络中的社团个数越多,且社团规模可能减小,即粗粒度下的社团在细粒度下可能被划分为多个社团,使社团结构产生很大变化。
3 实验设置与结果分析 3.1 数据及衡量指标本文所使用的数据包括公用数据和实例数据。公用数据为在清华大学ArnetMiner(研究者社会网络分析与挖掘系统)系统下载的数据Topic 131和Topic 145,是公用的合著网络数据集。以论文中的作者作为网络的节点,作者间的合著关系作为边。实例数据为CCF推荐国际学术会议A类的ICML会议从2005年到2014年共10年出版的论文,统计论文标题和文章作者信息,对数据进行处理,若两个作者出现在同一个文章里,则这两个作者之间有一条边,依据这些信息最后构建为一个合著网络,将数据集表示为ICML_10。
实验数据具体信息如表 1所示。
下面对本文用到的结构洞的度量指标进行介绍。
Rezvani等[17]根据伯特定义中的个体连接的社团数和个体的邻居节点数,提出一种新度量指标。伯特提出,一个好的结构洞占据者应该连接许多社团,但为了更有影响力,它连接的社团数和它的邻居节点数之比应该要大。Rezvani等在网络社团结构已知的情况下,根据这个定义提出一个ρ(S)指标(本文中称为结构洞跨越程度指标)来衡量结构洞占据者。给定图G=(V,E),假设S为找到的结构洞占据者集合,那么这个解集的质量如式(3)所示:
\[\rho (S)=\frac{\sum{_{\upsilon \in S}\frac{com(\upsilon )}{\deg (\upsilon )}}}{|S|}\]
(3)
考虑到数据集的规模和网络结构的合理性,分别求得3种粒度的层次社团结构,由粗到细分别表示为C1、C2和C3,其中C1是模块度最优时的网络划分,C2和C3是对C1进行逐次细化得到的社团结构。使用MG_MaxD方法发现不同粒度下的前20个结构洞占据者,根据ρ(S)指标计算不同粒度下的节点跨越结构洞程度,最后分析不同粒度下结构洞解集的质量。使用EAGLE算法在不同粒度下进行社团划分,得到Topic 131数据集在不同粒度下的社团划分个数为|C1|=32,|C2|=97,|C3|=164。
从图 4可以看出,社团划分粒度越细,结构洞解集中的节点跨越结构洞的程度越大,且随着个数的增加,同一粒度下结构洞解集的质量也在不断下降,但细粒度下的解集质量总是保持最佳。Topic 131数据集上结构洞解集的ρ(S)指标结果对比如图 4所示。

|
| 图 4 Topic 131在MG_MaxD算法下不同粒度结构洞解集的质量(top 20) Fig. 4 Performance of structural holes for MG_MaxD on Topic 131 (top 20) |
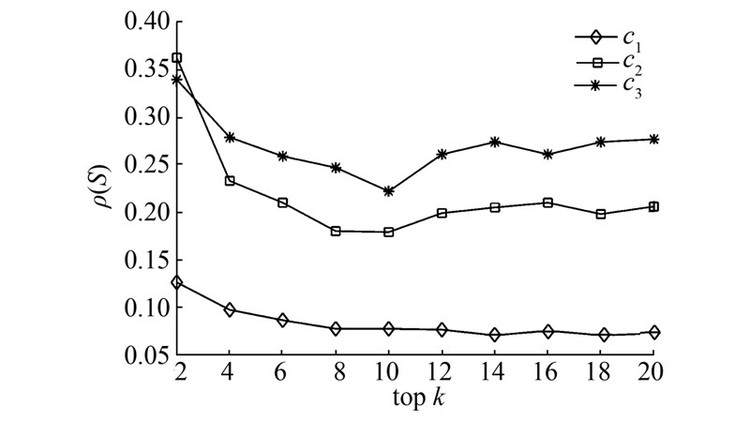
Topic 145数据集在不同粒度下的社团划分个数为|C1|=50 、|C2|=130、|C3|=251,分别发现不同粒度下的前20个结构洞占据者。Topic 145数据集上结构洞解集的ρ(S)指标结果对比如图 5所示。
|
| 图 5 Topic 145在MG_MaxD算法下不同粒度结构洞解集的质量(top 20) Fig. 5 Performance of structural holes for MG_MaxD on Topic 145 (top 20) |
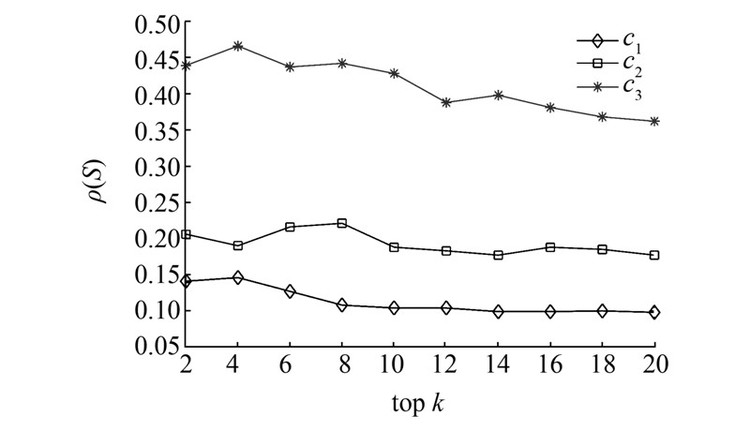
ICML_10数据集在不同粒度下的社团划分个数为|C1|=342、|C2|=565、|C3|=806,分别发现不同粒度下的前20个结构洞占据者,图 6显示 ICML_10数据集在不同粒度下找到的结构洞占据者的结构洞程度变化情况,随着社团划分粒度的变细,结构洞占据者解集的ρ(S)值变大。
|
| 图 6 ICML_10在MG_MaxD算法下不同粒度结构洞解集的质量(top 20) Fig. 6 Performance of structural holes for MG_MaxD on ICML_10 (top 20) |
通过图 4~6可以发现,细粒度下结构洞占据者解集的质量总是优于较粗粒度下的结构洞占据者。在Topic 131、Topic 145和ICML_10数据集上,当社团划分的粒度最粗时,由于此时的网络拓扑结构较为简单,社团数较少,而发现的结构洞占据者解集的效果并不好,说明此时个体的结构洞作用并不明显,即结构洞程度较低;而当粒度变细时,网络拓扑较为复杂,社团数较多,此时个体跨越的社团相对较多,可以更好得获得异质性信息和不同资源,且能更好的发挥结构洞作用,即细粒度下的结构洞占据者跨越结构洞的程度较大。对应于实际情况,将公司看作网络,而公司里还有许多不同部门,部门分为许多工作小组等等。粗粒度下将公司的部门作为节点,细粒度下可能将个体作为节点,这对应于不同粒度的层次结构,而个体在网络中的属性关系和结构洞程度会不断变化。
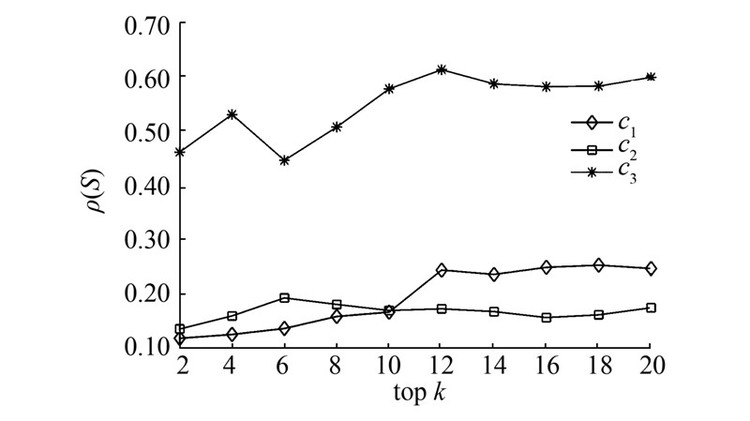
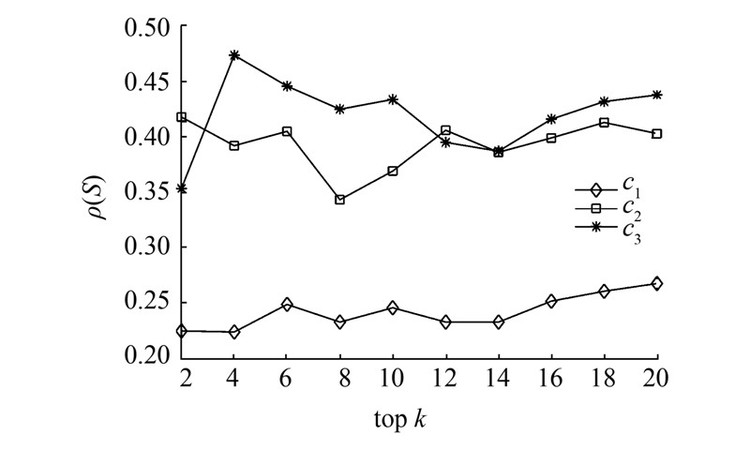
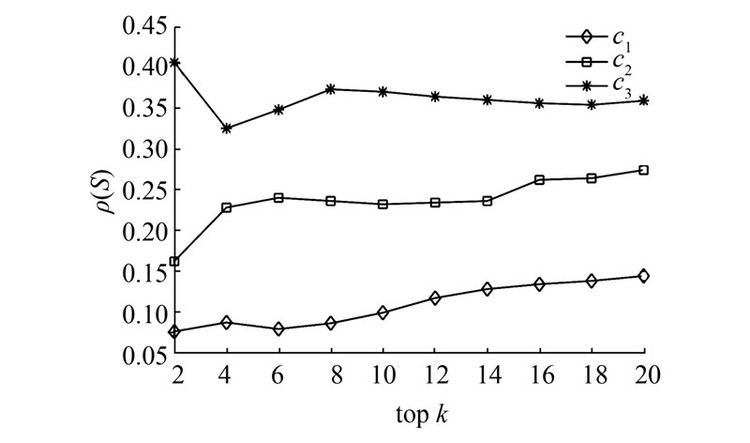
3.2.2 HIS对比实验结果为了验证上面结论的可靠性,本文使用文献[20]中的HIS算法进行对比试验,分别在Topic 131、Topic 145和ICML_10数据集上进行实验。当网络划分粒度变化时,网络社团结构也会发生变化,由于HIS算法中节点的重要性初始化是相对于社团的,所以HIS算法对社团结构的变化会更加敏感。使用HIS算法进行对比可以有效地验证上面结论。统计HIS算法在不同粒度下发现的结构洞,并使用ρ(S)指标对结构洞解集进行衡量,实验结果如图7~9所示。
|
| 图 7 Topic 131在HIS算法下不同粒度结构洞解集的质量(top 20) Fig. 7 Performance of structural holes for HIS on Topic 131 (top 20) |
|
| 图 8 Topic 145在HIS算法下不同粒度结构洞解集的质量(top 20) Fig. 8 Performance of structural holes for HIS on Topic 145 (top 20) |
|
| 图 9 ICML_10在HIS算法下不同粒度结构洞解集的质量(top 20) Fig. 9 Performance of structural holes for HIS on ICML_10 (top 20) |
图 7~9显示在不同数据集上,使用HIS算法找到的前20个结构洞解集的 ρ(S)指标变化情况,可以发现随着社团划分粒度的变粗,HIS算法找到的结构洞解集的质量也随之下降。粒度越粗,结构洞解集的ρ(S)越低,则节点跨越的结构洞的可能性越低。说明不同粒度下的网络层次结构对节点的结构洞程度会产生重要影响。
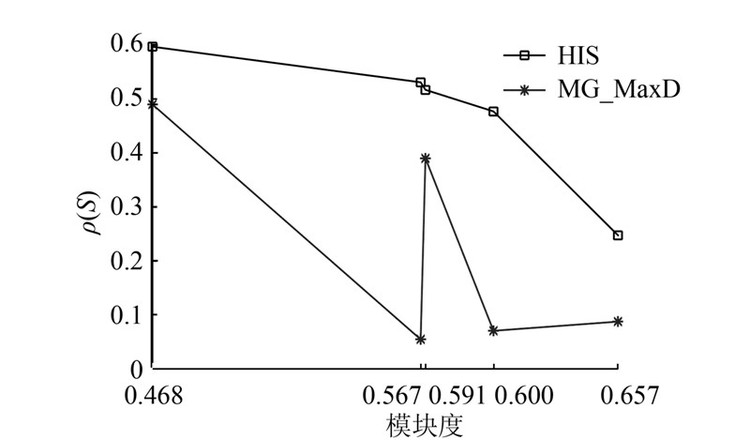
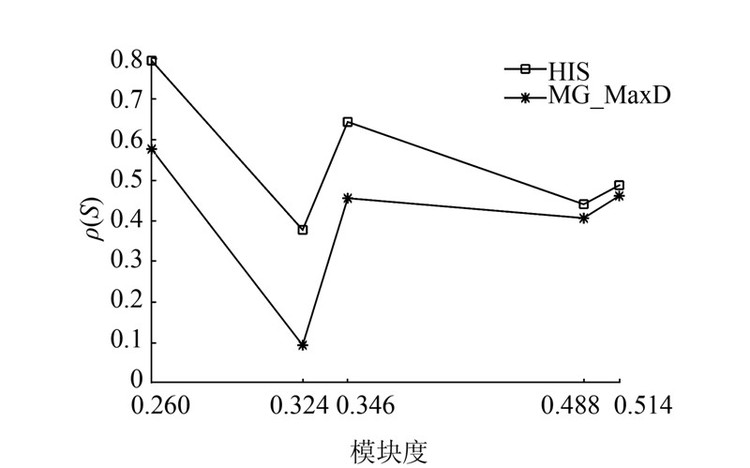
3.2.3 模块度及社团数对结构洞的影响本文在T131、T145数据集上,考虑多粒度下社团划分质量和结构洞解集质量之间的关系,即网络模块度和ρ(S)变化情况。选取MG_MaxD和HIS算法在两个数据集,和5种社团划分结果的模块度下发现的前20个结构洞占据者,实验结果如图 10和图 11所示。 从图 10和图 11可以看出,模块度越大说明社团划分结果越好,但结构洞解集质量不断降低。图 10显示在T131数据集中,当模块度为0.468时,此时社团划分质量最差,但MG_MaxD和HIS的结构洞解集的质量最佳,而随着模块度提高,这两个算法的解集质量也随之下降;图 11显示在T145数据集中也具有相同规律,且发现当模块度为0.324时,MG_MaxD和HIS的结构洞解集的质量最差。通过两组实验对比,可以发现模块度与结构洞解集的质量存在一定关系,在寻找网络中的结构洞解集的质量存在一定关系,在寻找网络中的结构洞时应结合社团划分结果的模块度因素,并选择合适的社团划分粒度。
|
| 图 10 T131数据集多粒度下不同算法对比结果(top 20) Fig. 10 Comparison of results of different algorithms on T131 in multi-granularity (top 20) |
|
| 图 11 T145数据集多粒度下不同算法对比结果(top 20) Fig. 11 Comparison of results of different algorithms on T145 in multi-granularity (top 20) |
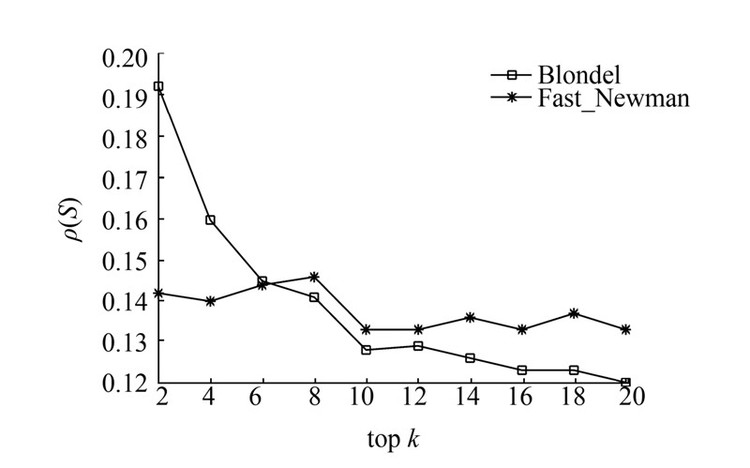
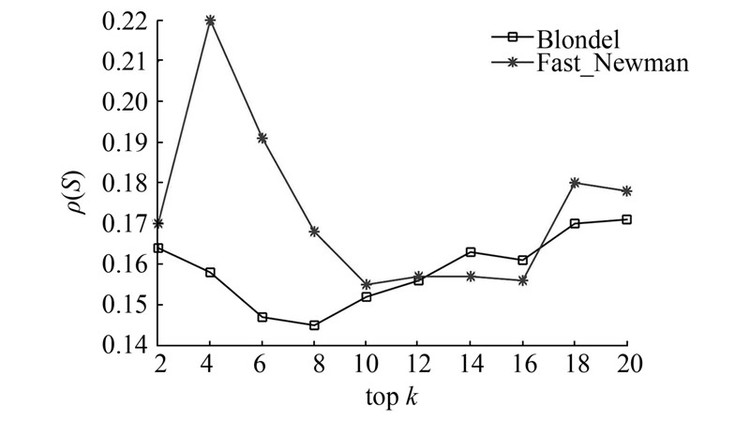
为验证单一粒度下社团数对结构洞解集质量的影响,本文使用Fast-Newman算法[27]和Blondel算法[28]分别对T131数据集和T145数据集的原网络进行社团划分,并获得单一粒度下相应的社团结构,使用MG_MaxD算法获得单一粒度下的结构洞占据者,最后对结构洞解集的质量进行分析。T131数据集在Blondel和Fast-Newman算法下分别得到25和30个社团,T145数据集在Blondel和Fast-Newman算法下分别得到16和30个社团。实验结果如图 12和图 13所示。
|
| 图 12 T131数据集在单粒度下对比结果(top 20) Fig. 12 Comparison of results of T131 in single granularity |
|
| 图 13 T145数据集在单粒度下的对比结果(top 20) Fig. 13 Comparison of results of T131in single granularity (top 20) |
图 12和图 13显示,由于单粒度下T131和T145数据集在两种社团划分算法下得到的社团数相差不大,得到的结构洞解集质量也很相近。可以发现在单一粒度下,社团数量对结构洞占据者跨越结构洞程度存在一定影响,从整体上看,当社团数增加时,结构洞解集质量也随之提高,即节点跨越结构洞的程度变大。
通过对比MG_MaxD算法和HIS算法在不同数据集上的实验结果,发现在同一网络下,不同的社团划分粒度会影响结构洞占据者的选取。所以在获取网络中的结构洞占据者时,由于不同社团划分粒度将影响节点跨越结构洞的程度,可以综合网络的多粒度社团划分结构,找到合适的粒度,发现更加准确的结构洞占据者。
4 结束语本文主要研究了多粒度对结构洞占据者跨越结构洞程度的影响,从社交网络的结构洞理论出发,考虑到不同社团划分粒度将影响结构洞占据者的选取,在多粒度社团划分的基础上,提出从多粒度角度分析结构洞占据者的方法。在不同数据集上进行实验,对结果进行分析,发现不同粒度的社团划分将影响节点跨越结构洞的程度。通过多组对比实验发现,在细粒度上,结构洞解集中的节点的结构洞程度较高,而在粗粒度上,由于将整个网络粗化,减弱了节点的结构洞效果。探讨多粒度下的结构洞占据者的结构洞程度的变化情况,可以帮助研究不同粒度下网络结构的优化、网络资源的有效获取和网络信息传播的有效控制。本文在结构洞理论和商空间模型的基础上,对多粒度网络社团的结构洞进行初步研究,发现不同粒度对节点的结构洞程度具有重要影响,且分析了模块度与结构洞占据者跨越结构洞程度之间的关系。根据结构洞跨越程度指标,结构洞解集质量随着社团数的增加而提高,然而社团数越多,社团结构却不一定最优,所以需要权衡社团划分粒度和结构洞跨越程度指标找到最优的结构洞占据者,这是未来研究的主要工作。
| [1] | BURT R S. Structural holes: The social structure of competition[M]//SWEDBERG R. Explorations in economic sociology. New York, USA: Russell Sage Foundations, 1993. |
| [2] | MA Ning, LIU Yijun, RUYA Tian, et al. Recognition of online opinion leaders based on social network analysis[M]//HUANG Runhe, GHORBANI A A, PASI G, et al. Active media technology. Berlin Heidelberg: Springer, 2012: 483-492. |
| [3] | YOO J, KIM W. The effect of structural holes on the corporate performance and strategic alliances network in pharmaceutical industry[J]. International proceedings of economics development and research, 2013, 67(5): 20-24. |
| [4] | CAI Penghua, ZHAO Hai, LIU Hong, et al. Research and analysis of structural hole and matching coefficient[J]. Journal of software engineering and applications, 2010, 3(11): 1080-1087. |
| [5] | TAN YONG, MOOKERJEE V S, SINGH P V. Social capital, structural holes and team composition: collaborative networks of the open source software community[C]//Proceedings of the international conference on information systems. Montreal, Quebec, Canada, 2007: 155. |
| [6] | SHIPILOV A V, LI S X. Can you have your cake and eat it too? Structural holes' influence on status accumulation and market performance in collaborative networks[J]. Administrative science quarterly, 2008, 53(1): 73-108. |
| [7] | RODAN S. Structural holes and managerial performance: identifying the underlying mechanisms[J]. Social networks, 2010, 32(3): 168-179. |
| [8] | KLEINBERG J. Strategic network formation with structural holes[C]//Proceedings of the 9th ACM conference on electronic commerce. New York, USA, 2008: 284-293. |
| [9] | BUSKENS V, VAN DE RIJT A. Dynamics of networks if everyone strives for structural holes1[J]. American journal of sociology, 2008, 114(2): 371-407. |
| [10] | GOYAL S, VEGA-REDONDO F. Structural holes in social networks[J]. Journal of economic theory, 2007, 137(1): 460-492. |
| [11] | BRUGGEMAN J, CARNABUCI G, VERMEULEN I. A note on structural holes theory and niche overlap[J]. Social networks, 2003, 25(1): 97-101. |
| [12] | BURT R S. Structural holes and good ideas1[J]. American journal of sociology, 2004, 110(2): 349-399. |
| [13] | BURT R S. Le capital social, les trous structuraux entrepreneur[J]. Revue francaise de sociologie, 1995, 36(4): 599-628. |
| [14] | FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41. |
| [15] | NEWMAN M E J, WATTS D J, STROGATZ S H. Random graph models of social networks[J]. Proceedings of the national academy of sciences of the united states of America, 2002, 99(3 Suppl. 1): 2566-2572. |
| [16] | 邓世果, 吴干华, 杨会杰. 基于基尼系数的网络结构洞测量[J]. 上海理工大学学报, 2011, 33(5): 452-456.DENG Shiguo, WU Ganhua, YANG Huijie. Gini-coefficient-based measurement of structural holes[J]. Journal of university of shanghai for science and technology, 2011, 33(5): 452-456. |
| [17] | REZVANI M, LIANG Weifa, Xu Wenzheng, et al. Identifying top-k structural hole spanners in large-scale social networks[C]//Proceedings of the 24th ACM international on conference on information and knowledge management. Melbourne, Australia, 2015: 263-272. |
| [18] | ZHANG Ende, WANG Guoren, GAO Kening, et al. Generalized structural holes finding algorithm by bisection in social communities[C]//Proceedings of the 2012 6th international conference on genetic and evolutionary computing. Washington, DC, USA, 2012: 276-279. |
| [19] | HU Renjie, ZHANG Guangyu. Structural holes in directed fuzzy social networks[J]. Journal of applied mathematics, 2014, 2014: 452063. |
| [20] | LOU Tiancheng, TANG Jie. Mining structural hole spanners through information diffusion in social networks[C]//Proceedings of the 22nd international conference on World Wide Web. New York, NY, USA, 2013: 825-836. |
| [21] | 韩忠明, 吴杨, 谭旭升, 等. 面向结构洞的复杂网络关键节点排序[J]. 物理学报, 2015, 64(5): 058902.HAN Zhongming, WU Yang, TAN Xusheng, et al. Ranking key nodes in complex networks by considering structural holes[J]. Acta physica sinica, 2015, 64(5): 058902. |
| [22] | 苏晓萍, 宋玉蓉. 利用邻域“结构洞”寻找社会网络中最具影响力节点[J]. 物理学报, 2015, 64(2): 020101.SU Xiaoping, SONG Yurong. Leveraging neighborhood “structural holes” to identifying key spreaders in social networks[J]. Acta physica sinica, 2015, 64(2): 020101. |
| [23] | CHEN Fengjiao, LI Kan. Detecting hierarchical structure of community members in social networks[J]. Knowledge-based systems, 2015, 87: 3-15. |
| [24] | SHEN Huawei, CHENG Xueqi, CAI Kai, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica a: statistical mechanics and its applications, 2009, 388(24): 5045-5056. |
| [25] | JIANG Feng, CHEN Yuming. Outlier detection based on granular computing and rough set theory[J]. Applied intelligence, 2015, 42(2): 303-322. |
| [26] | QIAN Jiangbo, ZHU Qiang, CHEN Huahui. Multi-granularity locality-sensitive bloom filter[J]. IEEE transactions on computers, 2015, 64(12): 3500-3514. |
| [27] | NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical review E, 2004, 69(6): 066133. |
| [28] | BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of statistical mechanics: theory and experiment, 2008, 30(2): 155-168. |



