2. 桂林电子科技大学 广西可信软件重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin 541004, China
随着互联网的迅速发展,用户越来越喜欢到相关网站上寻找自己想要的信息。以旅游领域为例,有机构预计2016年中国在线旅游市场规模将达到4 440亿元。游客访问旅游网站,寻找他们感兴趣的旅游信息,确定他们想去游玩的景点[1]。但是,旅游网站上信息过载严重,游客不容易从纷繁的旅游信息中选择合适自己需求的信息。进入Web 2.0时代,搜索和推荐为减轻用户寻找符合自己需要信息的困难提供了可能,其中利用用户的历史信息来预测用户选择的个性化推荐系统成为一种解决信息过载问题的有效工具[2, 3, 4, 5]。现今,商家广泛使用个性化推荐系统来对潜在的消费者进行物品、服务或信息的推荐。例如,亚马逊使用基于物品的协同过滤系统[6]进行个性化书本推荐;Google利用用户的点击行为数据建立了新闻推荐系统[7];百度开发了Q&A社区的推荐系统[8]等。
近些年,根据物理动力学原理设计的HC算法,已经被成功地应用到了推荐领域。HC算法将用户与物品的关系用一个二部网络来表示。但是,HC算法也存在一些不足。在HC算法中,目标用户喜欢的物品产生的热量在两步传播过程中被分别除以了用户的度和物品的度,所以它削弱了度数大的用户喜欢的度数大的物品对目标用户选择物品时的影响。事实上,目标用户对物品的选择往往受到与他关联的经历丰富的用户(度数大的用户)喜欢的流行物品(度数大的物品)较大的影响。以旅游推荐为例,如果某用户不是很清楚什么样的旅游产品适合自己,他会愿意听取旅游经历丰富的游客的意见,而旅游经历丰富的游客一般会推荐该用户自己喜欢的而且比较流行的景点(度数大的景点)。
本文主要做了如下研究:一是增大与目标用户关联的经历丰富的用户以及这些用户喜欢的流行物品对目标用户选择物品的影响,从而提出了HC的改进算法THC;二是在旅游领域为了更准确地判断用户是否喜欢一个景点,采用了综合评价的方法。本文根据用户对景点的整体评分、风景评分、趣味评分、性价比评分以及用户对景点评论的情感极性来判断用户是否真的喜欢该景点,从而提出了旅游推荐领域的用户态度判断算法。
1 相关工作迄今为止,众多的推荐系统研究者已经提出很多算法,如基于协同过滤的方法[6, 7, 8, 9]、基于内容分析的方法[10]、链接预测方法[11, 12]及混合方法[13]。文献[14]发现协同过滤算法(CF)推荐的TOP-n个物品更倾向于流行的物品,但是较少关注用户可能潜在感兴趣的物品[15]。为了克服CF的弱点,文献[13]提出了热传导(HC)算法来解决推荐系统中的准确性-多样性两难问题。文献[16]提出的物质扩散(MD)算法,是一种类似于HC的推荐算法,它能带来较高的准确率。文献[17]认为MD算法与HC算法分别在准确率和多样性上有优势,他们分析了不同度的物品在传播过程中的影响并引入一个参数控制影响程度,提出了一种混合算法。文献[18]认为用户从不同流行度的物品上获得的热量应该不同,它们利用一个参数来调控物品流行度对用户获得热量的影响并提出了非平衡热传导推荐算法。文献[19]发现,HC算法中所有不同度的物品和用户都被同等看待。因此,他们利用边连接的用户与物品的度来衡量边的权重,并提出了基于权重的HC算法(WHC);但是该算法将用户和物品的度对权重的影响程度视为相同。文献[5]认为HC算法的准确率较低是由于它倾向于推荐度数小的物品。为降低度数小的物品对目标用户推荐的影响,他们提出了基于偏向的热传导算法(BHC)。BHC算法通过降低度数小的物品的影响,来优先推荐度数大的物品,但是削弱了度数大的用户对目标用户的影响。相对于WHC算法而言,THC算法将用户与物品的度对目标用户选择物品的影响区别对待;相对于BHC算法而言,THC算法不仅考虑到了物品的度对目标用户选择物品的影响,还考虑到了用户的度对目标用户的影响。
2 热传导算法假设一个推荐系统中包含m个物品和n个用户,物品集合O={o1,o2,…,om},用户集合 U={u1,u2,…,un},那么一个推荐系统中用户与物品的关系就可以用一个包含m+n个节点的二部网络表示,如图 1(a)。其中,当且仅当一个用户喜欢一个物品时,这个物品与这个用户间才有边。任意两个物品间的边和任意两个用户间的边都是不允许存在的。这个结构也能用一个 A={aθl}m,n的矩阵表示,其中当且仅当用户ul喜欢物品oθ时aθl=1,反之aθl=0。
HC算法中,物品与物品间的热量是按如下方式传导的:用向量f代表网络中的以各用户作为目标用户时的初始热量赋值向量构成的矩阵,通过$\hat f$ =Wf来重新分配网络中的热量,其中W是一个代表热量传播过程的m×m概率矩阵;wγθ代表热量从物品oθ
到物品oγ的传导率;ki是用户i的度,kγ是物品γ的度;$\hat f$ i是$\hat f$ 的第i列,表示重新分配热量后对应于目标用户i的热量向量。将目标用户i没有表达喜欢意向的物品根据热量向量$\hat f$i中各元素的值进行降序排序。最终获得热量最多的TOP-n个物品被推荐给目标用户i。
${\omega _{\gamma \theta }} = \frac{1}{{{k_\gamma }}}\sum\limits_{i = 1}^n {\frac{{{a_{\gamma i}}{a_{\theta i}}}}{{{k_i}}}} $
(1)
图 1中给出了HC算法的示例。图 1(a)目标用户喜欢的物品被激活,被赋值热量1,其余的物品被赋值热量0;图 1(b)每个用户得到的热量是他喜欢的所有物品的热量均值;图 1(c)每个物品得到的热量是所有喜欢该物品的用户的热量均值。
 |
| 图 1 用户-物品二部网络中的热传导Fig. 1 Heat conduction in user-item bipartite network |
在推荐领域,目标用户对物品的选择与其相关联的经历丰富的用户有关。以旅游领域为例,比如:一个游客近期想准备一次旅游,由于他掌握的旅游信息有限,所以他很可能不太清楚去哪里游玩比较合适。他一般会咨询旅游经历丰富的朋友,了解他们曾经玩过的哪些景点比较好。这些旅游经历丰富的用户一般会建议他去游玩自己去过并且喜欢的一些流行的景点,该游客然后会综合他们的意见,从中选择自己想要去的景点。受到以上的启发,本文试图优先推荐与目标用户有关联的经历丰富的用户喜欢的度数大的物品。
基于上述考虑,本文提出了THC算法。
与HC算法不同的是:用户i接收到热量后不除以他自己的度ki而是除以kiλ;物品γ接收到热量后不除以它自己的度kγ,而是除以kγβ。因此,物品oθ到物品oγ的传导率就变成:
${\omega _{\gamma \theta }} = \frac{1}{{k_{_\gamma }^\beta }}\sum\limits_{i = 1}^n {\frac{{{a_{\gamma i}}{a_{\theta i}}}}{{k_{_i}^\lambda }}} $
(2)
从用户角度来分析,假设度为ki的用户i与度为kj的用户j(ki≥kj)均接收到1个单位的热量。在引入参数λ之前,用户i得到热量为1/ki,用户j得到 的热量为$\frac{1}{{{k_j}}}$。此时用户i与用户j得到的热量比就为$\frac{{{k_j}}}{{{k_i}}}$。引入参数λ后,他们得到的热量比就变为${\left( {\frac{{{k_j}}}{{{k_i}}}} \right)^\lambda }$。经过简单的分析可知:${\left( {\frac{{{k_j}}}{{{k_i}}}} \right)^\lambda } ≥ \frac{{{k_j}}}{{{k_i}}}$。这说明引入参数λ后,用户i与用户j得到热量的比增大了。而又由式(2)可知:引入参数λ后,所有用户接收到的热量都会增加。因此,度数大的用户得到的热量的增加程度更大。由指数函数的性质可知,当底数为0~1时,函数单调递减。因此当λ从1到0变化时,这种增加程度会越来越大。同样可以知道,引入参数β后所有物品接收到的热量都会增加,但是度数大的物品得到的热量的增加程度会更大。当β从1到0变化时,这种增加程度会越来越大。由以上分析可知:利用λ和β可以控制热传导过程中的传导率和热量的分配,也就是说:λ和β的引入可以控制度数大的用户喜欢的度数大的物品对目标用户推荐的影响。THC算法如下:
输入 用户-物品对数据集 T,推荐物品个数L,目标用户u;
输出 top-L个物品。
1)目标用户u喜欢的物品被激活,被赋值热量1;
2)热量按式(2)的传播方式从物品传到用户;
3)热量按式(2)的传播方式从用户传到物品;
4)物品按照其上面的热量按降序排序后,推荐给目标用户u top-L个物品。
4 旅游评价中的用户态度判断算法在推荐领域,有时仅凭一个单独的评分并不足以确定用户是否真的喜欢当前物品。以旅游领域为例,如图 2所示,某用户对某景点的整体评分为3,可以认为该用户喜欢该景点。但是,进一步观察发现:用户对当前景点的景色评分为4,对景点的趣味性、性价比的评分均为1。这说明用户对这个景点也有不满意的地方。用户对景点的态度也会体现在其对该景点的评论中。图 2给出的评论中出现了‘马达声吵死了’,‘大杀(煞)风景’及‘没有想象中的轻舟已过万重山的感觉’等文字。从评论中可以看出用户对这次旅游的体验并不满意。
 |
| 图 2 用户对景点评价和评论实例Fig. 2 An example ofausers evaluation and comment onascenery spot |
因此本文设计了确定用户是否喜欢某景点的算法,即旅游评价中的用户态度判断算法。设计理由如下:如果用户真的喜欢当前景点,那么该用户对当前景点的各项评分应该都比较高,则所有评分的均值也应该比较大。因此,计算各项评分的均值 sa,让均值大小作为判断用户是否喜欢该景点的依据之一。另外,如果用户真的喜欢当前景点,该用户对当前景点评论的情感一定会是非负向的。算法中,评论的情感极性计算方法采用文献[20]中的情感提取算法。以图 2为例,通过分析可知,根据整体评分会认为用户喜欢该景点,但用态度判断算法可以确定该用户对该景点并不是很满意,因为sa<3且评论的情感极性为负。使用旅游评价中的用户态度判断算法能较为准确地判断用户是否喜欢某景点。用户态度判断算法如下。
输入 用户对该景点的整体评分st; 用户对该景点的风景评分sg;用户对该景点的趣味评分si;用户对该景点的性价比评分sp;用户对该景点的评论信息C;
输出 true,用户喜爱该景点;false,用户不喜欢该景点。
1)利用ICTCLAS对C进行分词,去掉停用词,利用词性标注来去掉中性词;
2)对C中的其余词,判断其是否是情感词;
3)对每一个否定词wi,找出与其最近的情感词并且将其情感值从swi+1变成-swi+1;
4)对每一个程度副词,找出与其最近的情感词并且用程度副词对应的系数α乘以情感词的情感值;
5)利用如下公式计算评论C的情感极性值;
${S_c} = \sum\limits_{i = 1}^m {\alpha \times {S_{{\omega _i}}}} $
6)计算所有评分的均值Sa:
${S_a} = \frac{{\left( {{s_t} + {s_g} + {s_i} + {s_p}} \right)}}{4}$
7)如果Sa≥3且Sc≥0,返回true;否则返回 false。
5 实验与结果 5.1 数据集桂林是全国乃至世界知名的旅游目的地。本文从http://www.ctrip.com上抓取了关于桂林市旅游的数据来验证提出的算法。数据包含了用户对景点的评分和评论,评分包含了4个方面:用户对景点的整体评分、用户对景点的景色评分、用户对景点的趣味性评分以及用户对景点的性价比评分(如图 2)。本文采集了包含18 151个用户对143个景点的18 304条评分及评论记录。为了有效验证算法,对数据集进行了预处理。删除评价景点数量少于2条的用户,删除没有用户评分的景点,再利用旅游评价中的用户态度判断算法计算用户是否喜欢某景点。数据集包含1 164个用户对143个景点的5 672条评分及评论信息。
为了对提出算法的有效性进行更可靠的验证,本文还使用了电影评分的数据集[21]进行对比实验。删除对电影评分数目少于2条的用户,删除没有用户评分的电影,最终得到 370个用户对578部电影的9 331条评分记录。
每组实验中,数据集被分为2部分,其中随机挑选出用户-物品二部网络中20%的边作为测试集,其余80%的边为训练集[5]。每组实验都重复 50次,最终的实验结果是这50次实验结果的平均值。
5.2 评价指标
为了评判提出的想法是否达到了预期效果,即度数大的用户喜欢的度数大的物品是否被推荐出来。本文提出了一个大度用户大度物品率指标(buir),用来衡量推荐出的度数大的用户喜欢的度数大的物品出现在推荐列表中的比例。式(3)给出了目标用户i的该指标计算方法。
${\text{bui}}{{\text{r}}_{\text{i}}} = \frac{{\left| {{R_i} \cap {T_i}} \right|}}{L}$
(3)
为了分析提出算法的效果,本文采用了以下4个指标[5]:排序得分(ranking score)、新颖性(novelty)、多样性(diversity)及覆盖率(coverage)。
ranking score(RS):一个好的推荐算法应该将用户喜欢的物品排在前面。测试集中,如果物品
α被目标用户i喜欢,物品α位于用户i的推荐列表中排序为r的位置,那么物品α的排序得分为
$R{S_{i\alpha }} = \frac{r}{{m - {k_i}}}$
(4)
novelty:新颖性被定义为所有被推荐物品度的平均值。一个推荐算法的新颖性计算如式(5):
${\text{Novelty}} = \frac{{\sum\nolimits_{i = 1}^n {{k_i}} }}{n}$
(5)
diversity:一个推荐算法应该给不同的用户推荐不同的物品。式(6)给出了多样性的计算方法:
${H_{ij}} = 1 - \frac{{{Q_{ij}}\left( L \right)}}{L}$
(6)
coverage:推荐算法的覆盖率是指算法能推荐的物品种类占所有物品种类的比例。式(7)给出了覆盖率的计算方法:
${\text{Cov}} = \frac{n}{N}$
(7)
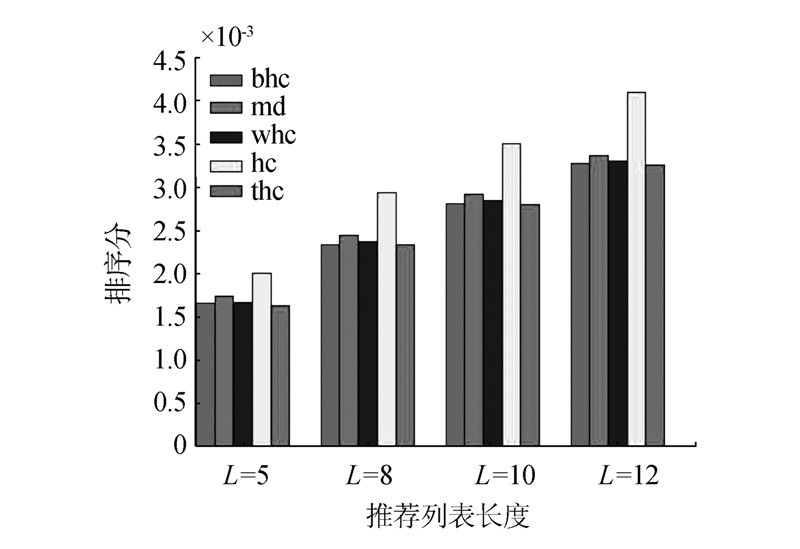
为了观察buir指标随参数λ和β的变化情况以及它对其他指标的影响,实验提供了THC算法分别在旅游数据集和电影数据集上推荐列表长度分别为 5、8、10、12时,各指标随参数变化的情况图。图分为8组,每组5张,共计40张。由于每组图的变化情况类似,本文只提供了推荐列表L=10时THC算法在旅游数据集上的结果,以分析buir与其他指标的关系。各指标的变化分别如图 3~7所示。 为了进一步分析THC方法的有效性,分别使用旅游数据集和电影评分数据集对BHC[5]、WHC[18]、MD[16]、HC[5]及THC在推荐列表的长度分别为5、8、10、12时的排序得分进行比较。实验结果如图 8、9所示。需要说明的是:某用户对某电影喜爱的条件是该用户对该电影的评分大于或等于3。某用户对某景点是否喜爱的判断是利用旅游评价中的用户态度判断算法计算得出。BHC和WHC中的参数变化范围为0~1。
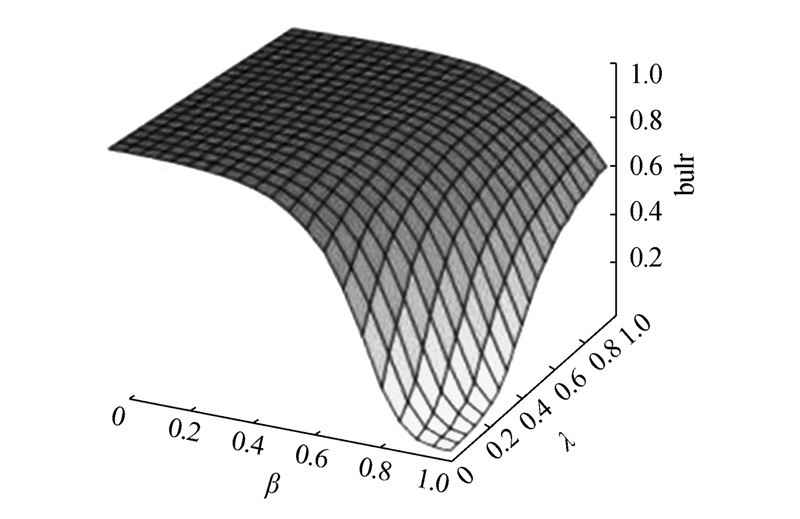 |
| 图 3 L=10时,THC算法在旅游评价数据集上buir指标随参数变化图Fig. 3 The variation of THC’s buir index on the travel data set when L=10 |
|
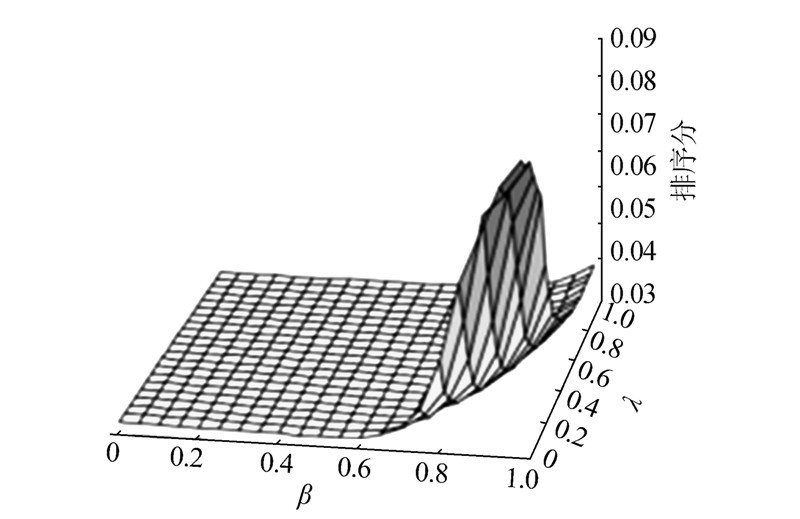
| 图 4 L=10时,THC算法在旅游评价数据集上排序得分指标随参数变化 Fig. 4 The variation of THC’s rank score index on the travel data set when L=10 |
|
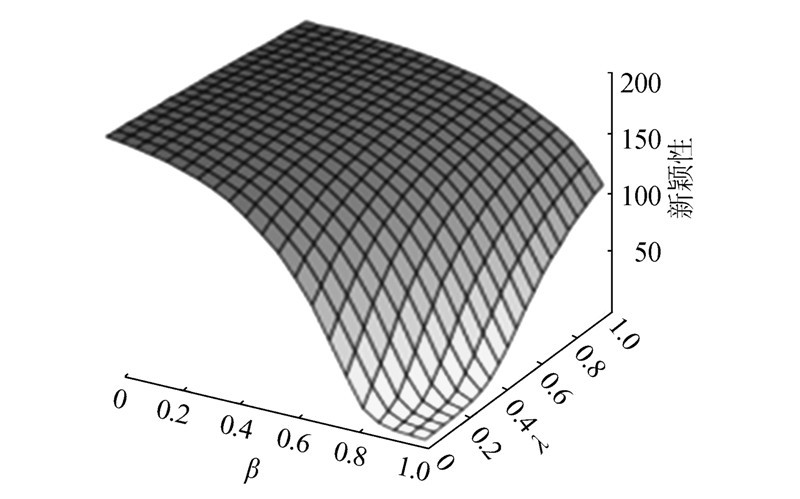
| 图 5 L=10时,THC算法在旅游评价数据集上新颖性指标随参数变化 Fig. 5 The variation of THC’s novelty index on the travel data set when L=10 |
|
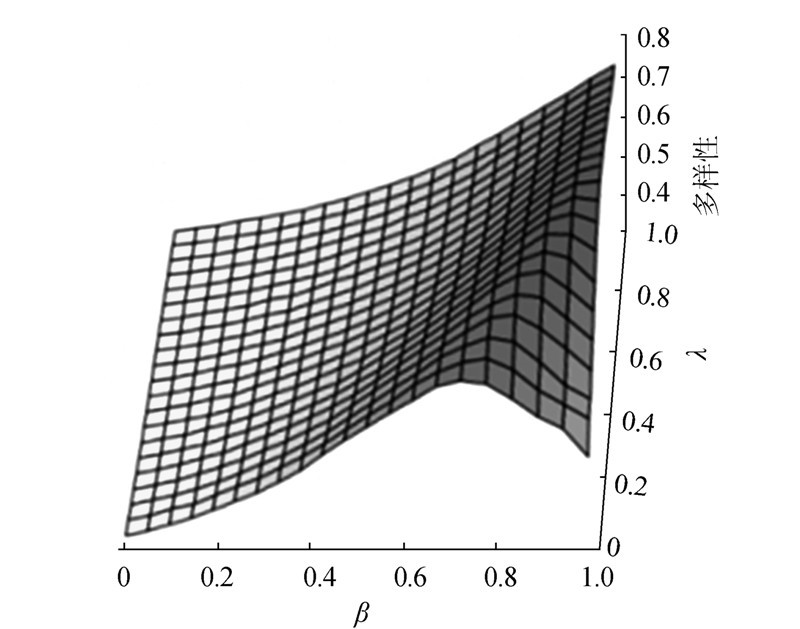
| 图 6 L=10时,THC算法在旅游评价数据集上多样性指标随参数变化 Fig. 6 The variation of THC’s diversity index on the travel data set when L=10 |

|
| 图 7 L=10时,THC算法在旅游评价数据集上覆盖率指标随参数变化 Fig. 7 The variation of THC’s coverage index on the travel data set when L=10 |
|
| 图 8 电影评分数据集上各算法的排序得分对比结果 Fig. 8 The comparison of rank score index on the movie data set |
|
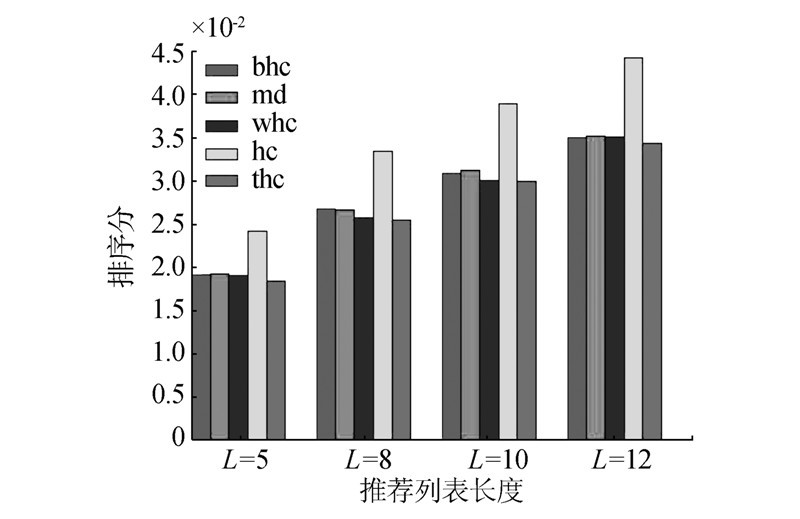
| 图 9 旅游评价数据集上各算法的排序得分对比结果 Fig. 9 The comparison of rank score index on the travel data set |
图 3~7中的黑色代表各图中相应指标值较大的区域,白色代表各图中相应指标值较小的区域,图中颜色越黑表示相应指标值越大。由图 3可以看出,当 λ取值小于0.5,β取值也小于0.5时,此时推荐出来的度数大的用户喜欢的度数大的物品较多。图 4中相应区域的排序得分较低,这说明度数大的用户喜欢的度数大的物品一般是大家所喜欢的物品,与文中开始提出的假设一致;由于此时推荐出来的度数大的物品较多,所以推荐的物品的新颖性较低即新颖性值较大,这与图 5中相应区域的指标数据是一致的;另外,度数大的用户喜欢的度数大的物品在整个系统的所有物品中占的比例是比较小的,因为大多数物品都不是流行物品,所以此时多样性和覆盖率都较低,这与图 6和图 7中相应区域的指标数据一致。对于图 4,数据表明:当 λ与β分别取0.05、0.55时,排序得分取得最优值0.029 8,但此时buir并不是最大。可以得出这样的结论:虽然目标用户会喜欢度数大的用户喜欢的度数大的物品,但是推荐的量要适度。还可以发现:此时的排序得分要比当λ=β=1.0时的HC算法的排序得分要好,而此时的buir指标也比HC的要高。
通过分析各个评价指标变化图,可以得出如下结论:1)如果要向用户推荐较多度数大的用户喜欢的度数大的物品,则应该将λ与β的取值范围都限制在0 ~0.5,因为在此范围中buir的值均较大。2)如果要使算法的排序得分取得最大值,2个参数λ 与β的最优值应该从0~1之间寻找。虽然λ与β 在0~0.5取值时,度数大的用户喜欢的度数大的物品更可能被推荐,但是并不一定是推荐得越多,排序得分越好。3)如果要向用户推荐较多的新颖物品,则不该将λ 与β的取值范围都限制在0~0.5,因为当 buir较大时,推荐出来的度数大的用户喜欢的度数大的物品较多,此时推荐出来的物品必然不新颖。
图 8和图 9是BHC、MD、WHC、HC及THC在两个数据集上推荐列表的长度分别为5、8、10、12时排序得分的对比结果。其中BHC、WHC及THC是取所有不同参数结果中的最优值。通过观察可以发现,本文提出的THC算法,与基本的HC算法相比,在所有的情况下排序得分都要好;与MD、WHC、BHC算法相比,排序得分也都要好,虽然提升程度较小。
通过上面的分析可以知道:通过适度的优先推荐度数大的用户喜欢的度数大的物品,有助于向用户推荐其喜欢的物品,从而有助于提升算法的效果。另外,还可以发现MD和BHC算法的排序得分在所有情形下都比HC算法要好,这与文献[5]中的结论一致;WHC算法在所有条件下都比HC算法的排序得分好,这与文献[19]中的结论一致。
6 结束语由于HC算法减弱了度数大的用户喜欢的度数大的物品对目标用户的影响,本文提出了基于影响力控制的热传导算法THC。THC引入2个参数来控制度数大的用户喜欢的度数大的物品被优先推荐的程度。为了检验提出的想法是否达到预期效果,在电影评分数据集和旅游评价数据集上进行了多项对比实验。本文还提出了旅游评价中的用户态度判断算法及一个新指标buir。实验结果表明,当THC中的2个参数 λ和β较小时,度数大的用户喜欢的度数大的物品能被更多的推荐,但这种推荐要有控制,否则会降低排序得分。实验结果还表明THC算法在排序得分指标上比BHC、MD、WHC及HC算法表现更好。未来可考虑结合用户间的朋友关系与信任关系进一步调控度数大的用户喜欢的度数大的物品对目标用户推荐的影响。
| [1] | 文益民, 史一帆, 蔡国永, 等. 个性化旅游推荐研究综述[EB/OL]. 北京: 中国科技论文在线, 2014. [2014-07-03]. http://www.paper.edu.cn/releasepaper/content/201407-56. |
| [2] | RESNICK P, VARIAN H R. Recommender systems[J]. Communications of the ACM, 1997, 40(3): 56-58. |
| [3] | ADOMAVICIUS G, TUZHILIN A. Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions[J]. IEEE transactions on knowledge and data engineering, 2005, 17(6): 734-749. |
| [4] | FELFERNIG A, GORDEA S, JANNACH D, et al. A short survey of recommendation technologies in travel and tourism[J]. OEGAI journal, 2007, 25(7): 17-22. |
| [5] | LIU Jianguo, ZHOU Tao, GUO Qiang. Information filtering via biased heat conduction[J]. Physical review E, 2011, 84(3): 037101. |
| [6] | LINDEN G, SMITH B, YORK J. Amazon. com recommendations: item-to-item collaborative filtering[J]. IEEE internet computing, 2003, 7(1): 76-80. |
| [7] | DAS A S, DATAR M, GARG A, et al. Google news personalization: scalable online collaborative filtering[C]//Proceedings of the 16th International Conference on World wide Web. New York, USA, 2007: 271-280. |
| [8] | LIU Qiwen, CHEN Tianjian, CAI Jing, et al. Enlister: baidu's recommender system for the biggest chinese Q & A website[C]//Proceedings of the Sixth ACM Conference on Recommender Systems. New York, USA, 2012: 285-288. |
| [9] | HERLOCKER J L, KONSTAN J A, RIEDL J. Explaining collaborative filtering recommendations[C]//Proceedings of the 2000 ACM Conference on Computer Supported Cooperative Work. New York, USA, 2000: 241-250. |
| [10] | PAZZANI M J. A framework for collaborative, content-based and demographic filtering[J]. Artificial intelligence review, 1999, 13(5-6): 393-408. |
| [11] | ZHOU Tao, Lü Linyuan, ZHANG Yicheng. Predicting missing links via local information[J]. The european physical journal B, 2009, 71(4): 623-630. |
| [12] | Lü Linyuan, ZHOU Tao. Link prediction in weighted networks: the role of weak ties[J]. EOL (europhysics letters), 2010, 89(1): 18001. |
| [13] | ZHOU Tao, KUSCSIK Z, LIU Jianguo, et al. Solving the apparent diversity-accuracy dilemma of recommender systems[J]. Proceedings of the national academy of sciences of the United States of America, 2010, 107(10): 4511-4515. |
| [14] | ZENG Wei, SHANG Mingsheng, ZHANG Qianming, et al. Can dissimilar users contribute to accuracy and diversity of personalized recommendation[J]. International journal of modern physics C, 2010, 21(10): 1217-1227. |
| [15] | ZHANG Zike, YU Lu, FANG Kuan, et al. Website-oriented recommendation based on heat spreading and tag-aware collaborative filtering[J]. Physica A: statistical mechanics and its applications, 2014, 399: 82-88. |
| [16] | ZHOU Tao, REN Jie, MEDO M, et al. Bipartite network projection and personal recommendation[J]. Physical review E, 2007, 76(4): 046115. |
| [17] | NIE Dacheng, AN Yahui, DONG Qiang, et al. Information filtering via balanced diffusion on bipartite networks[J]. Physica A: statistical mechanics and its applications, 2015, 421: 44-53. |
| [18] | 侯磊, 胡兆龙, 张博, 等. 基于流行度的非平衡热传导推荐算法研究[J]. 计算机应用研究, 2015, 32(11): 3235-3237. HOU Lei, HU Zhaolong, ZHANG Bo, et al. Information filtering via non-equilibrium heat conduction with consideration of popularity[J]. Application research of computers, 2015, 32(11): 3235-3237. |
| [19] | LIU Jianguo, GUO Qiang, ZHANG Yicheng. Information filtering via weighted heat conduction algorithm[J]. Physica A: statistical mechanics and its applications, 2011, 390(12): 2414-2420. |
| [20] | SHI Shaoliang, LI Yunpeng, WEN Yimin, et al. Adding the sentiment attribute of nodes to improve link prediction in social network[C]//Proceedings of the 12th International Conference on Fuzzy Systems and Knowledge Discovery. Zhangjiajie, China, 2015: 1263-1269. |
| [20] | LIU Jinhu, ZHANG Zike, CHEN Lingjiao, et al. Gravity effects on information filtering and network evolving[J]. PLoS one, 2014, 9(3): e91070. |



