网络流量分类是指识别网络中的各种应用与协议并对相关的网络流量进行分类的过程。网路流量分类是现代网络管理与安全系统中最基本的功能[1],在QOS服务质量控制、网络应用趋势分析、入侵检测等方面具有重大的作用。近年来,基于网络流量统计特征的机器学习分类方法受到了研究者的极大关注[2]。这类方法主要是利用网络流量在传输层的统计特征,根据实验或经验提取相关的特征属性再运用机器学习的方法进行分类。传统的机器学习方法在网络流量分类领域已有了应用,但依然存在如下问题:随着日益扩大的网络带宽与互联网用户规模,各类网络流量呈现出爆炸式的增长。现有的批处理方法在处理大规模网络流量分类问题时,其分类准确率与模型训练速率等通常难以取得平衡,模型训练时间将随着样本数量的增大而急剧上升。如何解决大规模网络流量分类问题已成为学者和业界人士面临的重大挑战。
在机器学习领域中,在线学习代表着一类利用一组有序的样本建立预测模型的高效的、大规模的算法。在线学习算法按时序一次处理一个或者一小批样本,处理过的样本不再处理也不再保存,这使得在线学习方法计算迅速且高效,更适合样本规模大且样本按时序到达并动态变化的应用场景。有些研究者认为,在线学习能够敏锐地捕捉到数据变化的趋势,进而解决数据非同分布和实时学习问题[3]。
针对高速骨干网上的大规模网络流量分类问题,本文将在线学习方法应用于网络流量分类问题,主要贡献有:
1)提出了一种基于在线学习的网络流量分类框架,在分类精度相当的条件下,在线学习方法比传统的支持向量机(SVM)方法有更好的分类效率;
2)对比了8种不同在线学习算法在网络流量分类应用中的分类性能差异,为应用打下了基础;
3)为了考察网络流量中样本顺序对分类效果的影响,对比了样本按时序处理与随机处理两种方式的差异,验证了网络流量样本存在着时序上的相关性。
1 相关研究近年来,基于流量统计特征的机器学习分类方法受到了研究者的极大关注[2]。这类方法主要是利用网络流量在传输层的统计特征,根据实验或经验提取相关的特征属性再运用机器学习的方法进行分类。基于统计特征的机器学习网络流量分类方法主要分为监督学习和无监督学习两类。监督学习方面,Moore等[4]提出了一种使用朴素贝叶斯的分类方法,分类准确率能达到约65%。Auld等[5]使用了贝叶斯神经网络的方法,并对特征集合进行了特征选择,使得分类精度得到了提高,分类准确率达到了95%。此外,还有一系列监督学习方法运用到了网络流量分类问题中:文献[6, 7]将支持向量机运用到了网络流量分类问题;文献[8, 9]运用了决策树理论。无监督学习方面,Zander等[10]提出了基于AutoClass的无监督网络流量分类方法,是一种基于EM算法的无监督贝叶斯分类器。Erman等[11]使用了EM聚类方法来解决流量分类问题,与贝叶斯分类方法相比有更高的分类准确率。这些算法都属于批处理的方法,在解决大规模网络流量分类问题时,存在着分类器训练慢、计算复杂度高的缺陷。
在线学习是一种解决大规模问题的有效手段。在线学习自提出以来,已应用于许多实际的应用场景中,例如垃圾邮件检测、在线广告推送、多媒体检索和金融时间序列预测。研究者们提出了大量的在线学习算法并进行了理论性证明。Rosenblatt于1958年提出的感知机算法[12]是最为人熟知的在线学习算法。Crammer等[13]提出的Passive-Aggressive(PA)算法也是一种著名的在线学习算法。为了提高在线学习算法的效率,研究者们提出了一系列的二阶在线学习算法[14]。与一阶算法不同,二阶算法通常假定权重向量服从一个高斯分布,并在每次迭代时尝试更新高斯分布的均值与方差。Confidence-Weighted (CW)算法[15]是一种典型的二阶算法。此外,还有许多基于CW算法的改进算法,Crammer等[16]提出了一种改进CW算法鲁棒性的AROW算法,Wang等[17]提出了Soft Confidence-weighted(SCW)算法。
本文提出的在线学习网络流量分类框架应用了8种在线学习算法。其中,一阶算法有感知机算法、在线梯度下降算法(OGD)、Passive-Aggressive算法(PA)以及两种基于PA的改进算法:PA-Ⅰ、PA-Ⅱ算法;二阶算法则选用了3种:Confidence-Weighted (CW)算法,以及基于CW算法改进的2种Soft Confidence-weighted(SCW)算法:SCW-Ⅰ、SCW-Ⅱ算法。
2 在线学习的网络流量分类框架 2.1 在线学习网络流量分类框架在线学习概念自提出以来发展出了一系列的算法,既能处理二分类问题又能处理多分类问题。为了验证在线学习方法在网络流量分类 问题中的有效性,本文将网络流量分类简化为一个二分类问题。下面将由在线学习二分类算法的一般流程出发,提出在线学习网络流量分类框架。
在线学习处理的数据是一种带有时序性的样本序列,其优化目标通常是最小化在整个样本序列下产生的累积误差。对于一个二分类问题,样本的特征X属于一个d维的特征空间,X=Rd;样本的类标Y为-1与+1,Y={-1,+1}。
在t时刻,分类器接收一个训练样本
xt∈
X,并计算样本的类标的预测值:
${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} _{\text{t}}}$=sgn(f
(xt;w
t))=sgn
(wt·x
t)∈Y
(1)
在做出预测后,分类器从环境中获取到样本的真实类标
yt∈Y,并通过一定的准则计算预测的损失(yt,${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} _{\text{t}}}$)。当损失大于0时,分类模型将按如下原则更新:
wt+1←Δ
(wt;(x
t,y
t))
(2)
在线学习不再区分训练阶段与测试阶段,在接收到新样本后对样本类别进行预测同时按照需要更新模型,其模型始终处于一个动态变化的过程,具有良好的实时性,能够跟踪数据流的变化趋势。在线学习需要在模型对样本进行预测后,能够即时获取到样本的真实类别。网络流量样本虽然是流式数据,但是样本的真实类别无法实时获取。为此,提出了一种按照在线学习方法训练分类器的网络流量分类框架,如图 1所示。训练阶段,该框架首先对实时网络流量进行抽样并通过特征提取与样本标记产生训练数据集,然后使用在线学习算法对分类模型进行训练。特征提取可使用Moore[3]提出的248维网络流统计特征,样本标记可使用深度包检测工具nDPI以及开源工具Tstat。测试阶段,该框架使用训练完成的模型对实时网络流量进行分类。将模型分类结果与nDPI与Tstat等工具的结果对比,当偏差达到一定阈值时对模型进行重新训练。
 |
| 图 1 在线网络流量分类框架Fig. 1 Online traffic classification scheme |
本框架在获取到完整训练集后离线训练在线学习分类模型。在线学习方法在优化理论中被称作增量算法。增量算法的主要思路是:当目标函数由一些子函数之和组成时,可以通过每次仅对一个子函数进行“首尾相接”依次传递式的梯度优化迭代而最终得到原问题的最优解。当按照随机的方式挑选子函数而不是按照顺序依次进行优化时,增量式方法可以称为随机优化方法[3]。在线学习与随机优化有很紧密的关系,在很多情况下,两者甚至等同使用[19]。在线和随机优化形式上虽然只是抽取样本方式上的区别,但研究表明,它们的收敛性存在着差异。另一方面,有研究者认为在线学习按顺序选择样本的方式能敏锐捕捉到数据变化的趋势。为了考察网络流量中样本顺序对分类效果的影响,本文在SCW-Ⅰ算法的基础上将顺序抽取样本的方式改为随机抽取的方式,实验对比了两者在网络流量分类问题中的差异,两种方法之间的效果差异表明了网络流量样本存在着时序上的相关性。
2.2 在线学习二分类算法为了检验本文提出的在线学习分类框架,我们选取了8种在线学习方法进行验证。所有的在线学习算法均满足表 1所示的在线学习算法一般流程,但由于理论基础不同,它们在损失函数、学习率、模型的更新条件以及方式有差异。
2.2.1 一阶算法感知机算法 感知机算法[12]于1958年提出,是最早最简单的一阶在线学习算法,其优化目标是:最小化学习到的分类器由当前样本带来的损失。感知机算法采用0-1损失作为损失函数,当损失大于0时,按照梯度下降的方式更新模型,其学习率恒为1。
OGD算法 在线梯度下降算法(OGD)[18]也是一种一阶算法,其优化目标与感知机算法一致,也是采用梯度下降的更新方式来优化由不同损失函数产生的优化目标。其与感知机算法的区别在于:OGD算法学习率 ηt设定为$\frac{C}{{\sqrt t }}$,其中C是大于0的学习率常数,t为迭代轮数。在 OGD算法的实现中我们使用了4种损失函数,分别为0-1损失、hinge损失、logistic损失和平方损失。在实验中可以发现,当使用hinge损失时,模型的分类效果最佳,因此我们在实验中均采用hinge损失。
PA算法 Passive-Aggressive算法[13]是一种比感知机算法和OGD算法更加复杂的一阶在线学习算法,其优化目标是如下两个目标的权衡:最小化学习到的分类器与之前的分类器的距离、最小化学习到的分类器由当前样本带来的损失。PA算法可以看作为如下的在线优化问题:
wt+1=arg $\mathop {\min }\limits_w \frac{1}{2}$‖
w-wt‖2,
s.t.(w;
(xt,yt))=max(0,1-yt(w·xt))=0
(3)
PA-Ⅰ算法可以看作如下优化问题:
wt+1=arg $\mathop {\min }\limits_w \frac{1}{2}$‖w-
wt‖2+C(w;(xt,yt))
(4)
PA-Ⅱ算法可以看作如式(5)形式:
wt+1=arg $\mathop {\min }\limits_w \frac{1}{2}$‖w-wt‖2+C(w;(xt,yt))2
(5)
为了更好地探索特征之间的深层结构,二阶算法通常假定权重向量服从一个高斯分布ω~N (μ,Σ),其中均值向量μ∈Rd,协方差矩阵Σ∈Rd×d。二阶算法在每次迭代时尝试更新高斯分布的均值与方差。
CW算法 CW算法由Crammer等[15]于2008年提出,该算法的权重分布N(μ,Σ)通过最小化新旧分布权重的KL散度来更新,并确保分类正确的概率大于一个阈值,可以看作如下优化问题:
(μt+1,Σ
t+1)=$\mathop {{\text{argmin}}}\limits_{\mu ,\sum } $DKL(N(μ,
Σ),N
(μt,Σt))
s.t. Pγw~N
(μ,Σ)[yt(w·xΣt)≥0]≥0
(6)
SCW算法 针对CW算法的局限,Wang等[17]于2013年提出了Soft Confidence-weighted算法。首先引入一种新的损失函数:
lφ(N
(μ,Σ);
(xt,yt))=max(0,φ$\sqrt {x_t^{\text{T}}\sum {x_t}} $-ytμ·xt)
(7)
(μt+1,Σ
t+1)=$\mathop {{\text{argmin}}}\limits_{\mu ,\sum } $DKL(N(μ,
Σ)||N
(μt,Σt))
s.t. lφ(N
(μ,Σ);
(xt,yt))=0,φ>0
(8)
原始的CW算法采取了一种非常激进的更新策略,即尽可能地改变分布以满足当前样本带来的约束。尽管这种方式有非常迅速的学习速率,但是在处理标记错误的样本时会导致分布的参数误修改。这就使CW算法在应用于有大量噪声的真实问题中时效果不理想。
SCW算法的提出克服CW算法的上述缺陷,具体的形式如下:
(μt+1,Σ
t+1)=$\mathop {{\text{argmin}}}\limits_{\mu ,\sum } $DKL(N(μ,
Σ)||N
(μt,Σt))+
Clφ(N
(μ,Σ);
(xt,yt))
(9)
(μt+1,Σ
t+1)=$\mathop {{\text{argmin}}}\limits_{\mu ,\sum } $DKL(N(μ,
Σ)||N
(μt,Σt))+
Clφ(N
(μ,Σ);
(xt,yt))2
(10)
一阶算法方面,感知机算法优化目标是最小化学习到的分类器由当前样本带来的损失,损失函数采用0-1损失,以定步长的梯度下降的方式来更新模型;OGD算法与感知机算法优化目标一致,但采用了4种不同的损失函数,梯度下降迭代的步长随迭代轮数增长而缩短;PA算法的优化目标是最小化学习到的分类器与之前的分类器的距离、最小化学习到的分类器由当前样本带来的损失。PA算法也使用了梯度下降来更新模型。PA-Ⅰ算法与PA-Ⅱ算法类似,均使用了一个参数C来调节两个目标的权重,只是PA-Ⅱ算法使用了平方约束项。
二阶算法则是假定权重向量服从高斯分布,每次迭代使用梯度下降尝试更新均值与方差。CW算法的优化目标是最小化新旧分布权重的KL散度来更新,并确保分类正确的概率大于一个阈值。SCW算法在CW算法中引入了新的损失函数,并使用了参数C来调节两个目标的权重。SCW-Ⅰ算法与SCW-Ⅱ算法区别在于PA-Ⅱ算法使用了平方约束项。
3 网络流量分类实验 3.1 实验数据集为了检验本文提出的在线学习分类框架的性能,本实验采用了Moore等在文献[3]中所使用的网络流量数据集,每个样本均是由一条完整的双向TCP流提取248维流量统计特征而来,实验中我们直接使用了完整的248维属性作为样本特征。该数据集采集了某网络出口24 h内10个时间段的双向流量数据,每个时间段的平均抽样时间约为1 680 s。该数据集共包含10种类别的377 526个网络流量样本,每种类别包含的流量和所占比例如表 1。
| 类别 | 数量 | 比例/% |
| WWW | 328 091 | 86.91 |
| 28 567 | 7.567 | |
| BULK | 11 539 | 3.056 |
| DATABASE | 2 648 | 0.701 |
| SERVICE | 2 099 | 0.556 |
| P2P | 2 094 | 0.555 |
| ATTACK | 1 793 | 0.475 |
| MEDIA | 1 152 | 0.305 |
| INT | 110 | 0.029 |
| GAME | 8 | 0.002 |
| 总计 | 377 526 | 100 |
由表 1可以看出,数据集中各类数据数量分布极不平均,WWW流量占据了数据集中的很高的比例。样本数量不平均问题对分类器的效果会有很大的影响,这是网络流量分类问题中的一个难点。本文重点不在于此,因此我们将数据集的样本分类简化为两类:一类为WWW流,另一类为其他应用。如表 2所示,本次实验所用实验数据集分为两组,一组是将10个子集独立的作为实验数据集,记为:Moore1~Moore10;另一组将10个子集按顺序合成为一个数据集,记为:MooreSet。为了模拟网络流量按序到达的特点,我们将数据集的前90%样本为训练集训练分类模型,后10%为测试集来测试模型效果。每个数据集的样本分布如表 2所示。
| 数据集 | 数量 |
|
| Moore1 | 24 863 | 16 130 | 6 247 | 2 081 | 405 |
| Moore2 | 23 801 | 16 841 | 4 580 | 1 718 | 662 |
| Moore3 | 22 932 | 16 036 | 4 603 | 2 029 | 264 |
| Moore4 | 22 285 | 17 647 | 2 410 | 1 994 | 234 |
| Moore5 | 21 645 | 17 183 | 2 301 | 1 435 | 729 |
| Moore6 | 19 384 | 15 505 | 1 941 | 1 387 | 551 |
| Moore7 | 55 835 | 46 682 | 3 570 | 5 300 | 283 |
| Moore8 | 55 494 | 46 526 | 3 419 | 5 169 | 380 |
| Moore9 | 66 248 | 53 782 | 5 842 | 6 211 | 413 |
| Moore10 | 65 036 | 48 386 | 10147 | 6 050 | 453 |
| MooreSet | 377 526 | 297 370 | 42 404 | 30 722 | 7 030 |
为了验证本文提出的在线学习网络分类框架的有效性,本文使用MATLAB 2015a用于数值计算,SVM的实现采用了Libsvm软件包,在线学习算法的实现采用了的LIBOL算法库[20]。实验采用普通台式电脑,操作系统为Windows 7 旗舰版,其中CPU为Intel i5处理器,内存4 GB。
3.3 评价指标网络流量分类系统的评价指标主要有两个方面:分类系统的效率与精度,效率意味着分类模型的训练时间足够短,消耗的存储空间能够被接受,精度意味着分类准确率较高,且漏报率与误报率控制在一定范围内。为了对比批处理方法与在线学习方法在网络流量分类问题中的性能差异,参考了文献[21]的做法,将在线学习算法与SVM算法进行对比,采用了模型训练时间、分类精度和F-measure为评价指标。
对于在线学习,模型训练过程中的支持向量数量也是一项重要的评价指标。支持向量是指在线学习模型训练过程中产生损失,并导致模型发生更新的样本。支持向量数量过少导致模型训练 比较粗糙,可能无法达到相应的精度;数量过多则会导致计算量增加,降低模型训练的效率。因此,在对比不同在线学习方法的性能时,增加了模型训练过程的支持向量数。在对比样本按时序处理与随机处理的训练过程的差异时,还采用了模型训练的累积错误率作为评价指标。
3.4 实验与分析为了评估本文提出的在线学习网络流量分类框架,本节设计了两个实验。实验1侧重于对比在线学习算法与SVM以及不同在线学习方法之间的性能差异。实验2侧重于考察网络流量中样本顺序对分类效果的影响,对比样本时序处理方式与随机处理方式的性能差异。
3.4.1 性能对比实验性能对比实验在10个数据子集与1个完整的数据集上,分别运行SVM算法与8种在线学习算法,使用每个数据集的前90%的样本作为训练集训练模型,使用后10%的样本作为测试集模拟模型实时运行的性能。实验结果及分析如下:
| s |
| 数据集 |
|
| Moore1 | 0.492 | 0.686 | 0.513 | 0.573 | 0.585 | 1.135 | 1.223 | 1.251 | 38.142 |
| Moore2 | 0.443 | 0.624 | 0.463 | 0.511 | 0.514 | 1.104 | 1.023 | 1.065 | 21.302 |
| Moore3 | 0.464 | 0.638 | 0.476 | 0.532 | 0.531 | 1.352 | 1.263 | 1.259 | 20.957 |
| Moore4 | 0.458 | 0.625 | 0.467 | 0.516 | 0.525 | 1.268 | 1.309 | 1.555 | 14.215 |
| Moore5 | 0.472 | 0.637 | 0.491 | 0.539 | 0.545 | 1.327 | 1.492 | 1.687 | 14.252 |
| Moore6 | 0.383 | 0.534 | 0.404 | 0.444 | 0.451 | 1.211 | 1.152 | 1.052 | 11.246 |
| Moore7 | 1.111 | 1.538 | 1.142 | 1.272 | 1.284 | 2.939 | 3.023 | 3.403 | 80.916 |
| Moore8 | 1.108 | 1.535 | 1.152 | 1.278 | 1.291 | 2.901 | 2.884 | 3.157 | 76.888 |
| Moore9 | 1.317 | 1.844 | 1.376 | 1.530 | 1.543 | 3.870 | 3.707 | 4.143 | 148.148 |
| Moore10 | 1.290 | 1.802 | 1.341 | 1.494 | 1.500 | 3.637 | 3.550 | 3.960 | 150.661 |
| MooreSet | 7.063 | 10.028 | 7.377 | 8.202 | 8.223 | 15.547 | 15.965 | 18.189 | 3 990.587 |
表 3列出了不同算法在不同数据集上的训练时间,由表可以看出:在线学习算法与SVM算法的模型训练时间存在相当大的差异,在线学习模型训练速度要远快于SVM算法,在样本数量大时,两者速度差别尤其明显。在使用完整数据集时,在线学习算法模型训练时间最多只需要18 s,而SVM算法则需要3 990 s,超过了1 h。另一方面,一阶在线学习算法与二阶在线学习算法在模型训练速度上也存在差异,二阶算法要比一阶算法略慢,其中可能的原因会在后文分析。
表 4列出了不同算法在不同数据集上的测试精度,对于每个数据集,用黑体标出了分类精度比SVM更差的在线算法;用星号标出了分类精度最好的算法。由表可以看出:在使用完整数据集时,SVM的分类精度比所有的在线学习算法都要好。但在使用10个子集进行实验时,二阶在线算法总体来说具有比SVM更好的分类效果,一阶算法在数据样本较少的前5个子集上的分类效果明显要差于SVM算法,尤其是OGD算法与感知机算法的分类效果最差,感知机算法在Moore3数据集上分类精度仅有0.452。后文将会解释OGD算法与感知机算法在数据样本少的情况下,分类精度差的原因。
| 数据集 |
|
| Moore1 | 0.969 | 0.955 | 0.977 | 0.976 | 0.977 | 0.967 | 0.988* | 0.98 | 0.952 |
| Moore2 | 0.773 | 0.821 | 0.819 | 0.813 | 0.823 | 0.946 | 0.980* | 0.976 | 0.847 |
| Moore3 | 0.452 | 0.957 | 0.963 | 0.954 | 0.959 | 0.973 | 0.986* | 0.981 | 0.956 |
| Moore4 | 0.714 | 0.919 | 0.844 | 0.883 | 0.873 | 0.965 | 0.972 | 0.974* | 0.954 |
| Moore5 | 0.901 | 0.924 | 0.907 | 0.920 | 0.921 | 0.987 | 0.995* | 0.994 | 0.925 |
| Moore6 | 0.969 | 0.959 | 0.973 | 0.974 | 0.975 | 0.966 | 0.993* | 0.99 | 0.95 |
| Moore7 | 0.986 | 0.975 | 0.980 | 0.981 | 0.981 | 0.984 | 0.993* | 0.992 | 0.981 |
| Moore8 | 0.982 | 0.973 | 0.982 | 0.981 | 0.981 | 0.983 | 0.991* | 0.991* | 0.974 |
| Moore9 | 0.978 | 0.967 | 0.978 | 0.979 | 0.980 | 0.983* | 0.982 | 0.981 | 0.97 |
| Moore10 | 0.975 | 0.981 | 0.982 | 0.982 | 0.982 | 0.980 | 0.986* | 0.984 | 0.977 |
| MooreSet | 0.953 | 0.928 | 0.872 | 0.939 | 0.907 | 0.915 | 0.959 | 0.968 | 0.978* |
表 5列出了不同算法在不同数据集上的F-measure,对于每个数据集,用黑体标出了F-measure比SVM更差的在线算法;用星号标出了F-measure最好的算法。从表 5可以得出与表 4一致的结论。表 6列出了8种不同在线算法在不同数据集上训练时的支持向量数。支持向量是指在线学习模型训练过程中产生损失,并导致模型发生更新的样本。支持向量越多表示模型更新次数越多,模型训练越充分,相应的计算量也越大。反之,则计算量更少,模型训练可能不够。这里尝试从支持向量数的角度解释上文中发现的二阶算法训练时间比一阶算法慢,但是效果比一阶算法好的现象。二阶算法的模型更加复杂,模型每次更新的计算量更大,由表 6可以看出,二阶算法的支持向量数比一阶算法略多,这就导致了二阶算法比一阶算法模型训练所需时间更长。感知机与OGD算法的支持向量数明显要少于其他在线算法,这导致了模型没有得到有效的训练,达不到其他算法相当的分类精度。我们注意到感知机算法的支持向量数最少,这可能是其分类精度极不稳定甚至分类精度非常低的原因。
| 数据集 |
|
| Moore1 | 0.982 | 0.973 | 0.987 | 0.986 | 0.986 | 0.980 | 0.993* | 0.993* | 0.971 |
| Moore2 | 0.849 | 0.850 | 0.851 | 0.852 | 0.853 | 0.854 | 0.855 | 0.856 | 0.857* |
| Moore3 | 0.552 | 0.975 | 0.979 | 0.974 | 0.976 | 0.985 | 0.992* | 0.992* | 0.986 |
| Moore4 | 0.812 | 0.954 | 0.906 | 0.931 | 0.925 | 0.981 | 0.985* | 0.985* | 0.975 |
| Moore5 | 0.925 | 0.943 | 0.930 | 0.941 | 0.941 | 0.990 | 0.996* | 0.996* | 0.946 |
| Moore6 | 0.978 | 0.972 | 0.981 | 0.982 | 0.983 | 0.976 | 0.995* | 0.995* | 0.966 |
| Moore7 | 0.992 | 0.987 | 0.990 | 0.990 | 0.990 | 0.991 | 0.996* | 0.996* | 0.991 |
| Moore8 | 0.990 | 0.985 | 0.991 | 0.990 | 0.990 | 0.991 | 0.995* | 0.995* | 0.986 |
| Moore9 | 0.988 | 0.982 | 0.988 | 0.989 | 0.989 | 0.991 | 0.991* | 0.991* | 0.984 |
| Moore10 | 0.987 | 0.990 | 0.991 | 0.990 | 0.991 | 0.989 | 0.992* | 0.992* | 0.988 |
| MooreSet | 0.971 | 0.958 | 0.915 | 0.962 | 0.940 | 0.950 | 0.975 | 0.975 | 0.987* |
| 数据集 |
|
| Moore1 | 277 | 947 | 1 056 | 1 099 | 1 621 | 895 | 863 | 1 063 |
| Moore2 | 209 | 847 | 864 | 888 | 1 139 | 844 | 744 | 812 |
| Moore3 | 210 | 819 | 921 | 933 | 1 366 | 812 | 594 | 746 |
| Moore4 | 244 | 772 | 954 | 982 | 1 452 | 882 | 768 | 1 127 |
| Moore5 | 237 | 609 | 953 | 960 | 1 385 | 796 | 812 | 1 304 |
| Moore6 | 206 | 585 | 844 | 862 | 1 214 | 735 | 663 | 555 |
| Moore7 | 405 | 1 624 | 1 475 | 1 591 | 2 384 | 1 405 | 1 332 | 2 149 |
| Moore8 | 393 | 1 318 | 1 446 | 1 489 | 2 167 | 1 317 | 1 160 | 2 102 |
| Moore9 | 837 | 1 672 | 2 426 | 2 515 | 3 476 | 2 120 | 2 071 | 3 242 |
| Moore10 | 531 | 1 542 | 1 924 | 1 962 | 2 954 | 1 787 | 1 590 | 2 645 |
| MooreSet | 2 904 | 7 716 | 10 074 | 9 892 | 14 344 | 9 525 | 6 265 | 15 825 |
通过性能对比实验可以发现,在8种在线学习分类算法中,二阶算法的分类效果普遍优于一阶算法,与SVM分类效果相当;SCW-Ⅰ算法有着较好的分类精度与分类效率,具有良好的应用前景。
3.4.2 时序相关性实验为了考察网络流量中样本顺序对分类效果的影响,我们将训练数据集中样本的顺序随机打乱,再用在线学习算法去训练模型。本实验使用10个数据子集作为实验数据集,将分类性能最好的SCW-Ⅰ算法分别用样本按时序处理与随机处理的方式进行训练,然后使用测试集进行测试。其中,随机处理方式按照不同的随机顺序重复实验20次,对实验结果取平均。实验还使用了模型训练过程中的累积错误率作为评价指标。时序方式与随机方式对比见表 7。
| 数据集 |
|
| Moore1 | 0.008 | 0.010 | 0.988 | 0.982 | 0.993 | 0.989 | 1.223 | 1.189 |
| Moore2 | 0.010 | 0.006 | 0.98 | 0.976 | 0.855 | 0.984 | 1.023 | 1.091 |
| Moore3 | 0.004 | 0.006 | 0.986 | 0.986 | 0.992 | 0.992 | 1.263 | 1.274 |
| Moore4 | 0.008 | 0.008 | 0.972 | 0.976 | 0.985 | 0.987 | 1.309 | 1.467 |
| Moore5 | 0.007 | 0.007 | 0.995 | 0.993 | 0.996 | 0.995 | 1.492 | 1.510 |
| Moore6 | 0.006 | 0.007 | 0.993 | 0.992 | 0.995 | 0.994 | 1.152 | 1.327 |
| Moore7 | 0.008 | 0.006 | 0.993 | 0.994 | 0.996 | 0.997 | 3.023 | 3.686 |
| Moore8 | 0.005 | 0.006 | 0.991 | 0.991 | 0.995 | 0.995 | 2.884 | 3.479 |
| Moore9 | 0.010 | 0.011 | 0.982 | 0.984 | 0.991 | 0.992 | 3.707 | 4.685 |
| Moore10 | 0.008 | 0.010 | 0.986 | 0.985 | 0.992 | 0.992 | 3.550 | 4.311 |
| MooreSet | 0.007 | 0.008 | 0.959 | 0.967 | 0.975 | 0.980 | 15.965 | 17.692 |
表 7对比了SCW-Ⅰ算法时序方式与随机方式在不同数据集下的性能指标,用黑体标出了较好的指标。由表可以看出:在网络流量分类问题中,时序方式比随机方式有更低的训练累积错误率、较好的测试精度与F-measure、更快的模型训练时间。这表明网络流量的样本顺序对分类效果有正面影响,因此可以认为网络流量样本存在着一种时间上的相关性,这种特性对分类效率的提高有积极意义。
为了说明此种相关性,在模型训练过程中按照样本数量间隔设置了15个采样点,记录了在线方式与随机方式训练过程中训练错误率的变化趋势。我们选取了第4、6、8、10个子集的一次实验结果,绘制了模型训练累积错误率的趋势,如图 2所示。
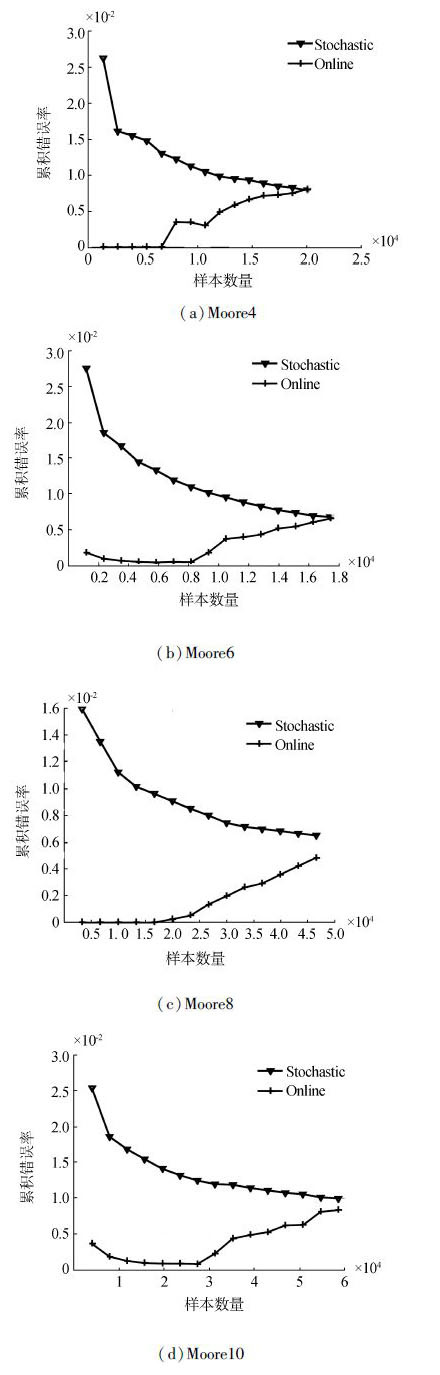 |
| 图 2 训练累积错误率Fig. 2 Training cumulative mistake rate |
由图 2可以看出,模型训练过程中,随机方式与时序方式的累积错误率的变化趋势有很大的不同。两种方法不仅是收敛速度的差异,随机方式的累积错误率的变化趋势是一个缓慢下降的过程,而在线方式的变化趋势却是一个曲折上升的过程,且每个数据集的曲线都有各自的结构特点。
由此可以发现,网络流量样本中存在着一种时间上的相关性,对模型的分类效果有一定的正面影响。但这种特性还缺乏理论性的分析,同时如何运用这种特性还需要进一步研究。
4 结束语本文针对高速骨干网大规模网络流量分类问题提出了一种基于在线学习的网络流量分类框架,并将8种在线学习方法运用到网络流量分类问题中。对比在线算法与批处理方法SVM的性能差异,实验表明在分类精度相当的情况下,在线学习算法与SVM相比空间开销小、模型训练时间显著缩短;对比不同在线学习方法的分类性能,实验表明SCW-Ⅰ算法在8种在线学习算法中有最好的分类效果;对比样本时序处理方式与随机处理方式的差异,实验表明网络流量样本中存在着一种时间序列上的相关性。
本文发现的网络流量样本的相关性只是通过实验来验证,缺乏理论分析,也没有找到合适的利用方法。另一方面,本文仅使用了二分类在线算法在实验数据集上进行验证,如何把算法扩展到多分类并实际应用于大规模网络环境是下一步工作的重点。
| [1] | ZHANG Jun, CHEN Xiao, XIANG Yang, et al. Robust network traffic classification[J]. IEEE/ACM transactions on networking, 2015, 23(4): 1257-1270. |
| [2] | NGUYEN T T T, ARMITAGE G. A survey of techniques for internet traffic classification using machine learning[J]. IEEE communications surveys & tutorials, 2008, 10(4): 56-76. |
| [3] | 陶卿, 高乾坤, 姜纪远, 等. 稀疏学习优化问题的求解综述[J]. 软件学报, 2013, 24(11): 2498-2507. TAO Qing, GAO Qiankun, JIANG Jiyuan, et al. Survey of solving the optimization problems for sparse learning[J]. Journal of software, 2013, 24(11): 2498-2507. |
| [4] | MOORE A W, ZUEV D. Internet traffic classification using bayesian analysis techniques[J]. ACM sigmetrics performance evaluation review, 2005, 33(1): 50-60. |
| [5] | AULD T, MOORE A W, GULL S F. Bayesian neural networks for internet traffic classification[J]. IEEE transactions on neural networks, 2007, 18(1): 223-239. |
| [6] | ESTE A, GRINGOLI F, SALGARELLI L. Support vector machines for TCP traffic classification[J]. Computer networks, 2009, 53(14): 2476-2490. |
| [7] | SCHATZMANN D, MüHLBAUER W, SPYROPOULOS T, et al. Digging into HTTPS: flow-based classification of webmail traffic[C]//Proceedings of the 10th ACM SIGCOMM conference on internet measurement. New York, NY, USA, 2010: 322-327. |
| [8] | WANG Yu, YU Shunzheng. Supervised learning real-time traffic classifiers[J]. Journal of networks, 2009, 4(7): 622-629. |
| [9] | NGUYEN T T T, ARMITAGE G, BRANCH P, et al. Timely and continuous machine-learning-based classification for interactive IP traffic[J]. IEEE/ACM transactions on networking, 2012, 20(6): 1880-1894. |
| [10] | ZANDER S, NGUYEN T, ARMITAGE G. Automated traffic classification and application identification using machine learning[C]//Proceedings of the IEEE conference on local computer networks 30th anniversary. Sydney, NSW, Australia, 2005: 250-257. |
| [11] | ERMAN J, ARLITT M, MAHANTI A. Traffic classification using clustering algorithms[C]//Proceedings of the 2006 SIGCOMM workshop on mining network data. New York, NY, USA, 2006: 281-286. |
| [12] | ROSENBLATT F. The perception: a probabilistic model for information storage and organization in the brain[J]. Psychological review, 1958, 65(6): 386-408. |
| [13] | CRAMMER K, DEKEL O, KESHET J, et al. Online passive-aggressive algorithms[J]. Journal of machine learning research, 2006, 7(3): 551-585. |
| [14] | CESA-BIANCHI N, CONCONI A, GENTILE C. A second-order perceptron algorithm[J]. SIAM journal on computing, 2005, 34(3): 640-668. |
| [15] | CRAMMER K, DREDZE M, PEREIRA F. Exact convex confidence-weighted learning[C]//Advances in neural information processing systems 21. Mountain View, CA, USA, 2008: 345-352. |
| [16] | CRAMMER K, KULESZA A, DREDZE M. Adaptive regularization of weight vectors[J]. Machine learning, 2013, 91(2): 155-187. |
| [17] | WANG Jialei, ZHAO Peilin, HOI S C H. Exact soft confidence-weighted learning[C]//Proceedings of the 29th international conference on machine learning. Edinburgh, Scotland, UK, 2012. |
| [18] | ZINKEVICH M. Online convex programming and generalized infinitesimal gradient ascent[C]//Proceedings of the international conference on machine learning. Washington, DC, USA, 2003: 928-936. |
| [19] | CESA-BIANCHI N, CONCONI A, GENTILE C. On the generalization ability of on-line learning algorithms[J]. IEEE transactions on information theory, 2004, 50(9): 2050-2057. |
| [20] | HOI S C H, WANG Jialei, ZHAO Peilin. LIBOL: a library for online learning algorithms[J]. Journal of machine learning research, 2014, 15(1): 495-499. |
| [21] | LU Jing, HOI S C H, WANG Jialei, et al. Large scale online kernel learning[J]. Journal of machine learning research, 2014, 1: 1-48. |



