传统的聚类算法在拥有大量数据的情况下能够在不同的场景下发挥各自的作用,当数据匮乏、噪声污染的情况,传统的聚类算法存在着不足。
近年来,迁移学习的成果逐渐丰富,研究表明,迁移学习能够有效地解决数据量不足、数据受污染和信息丢失等问题。文献[1]根据迁移学习中源领域和目标领域中是否含有标签,可以将迁移学习划分为3类:归纳迁移学习、直推式迁移学习和无监督迁移学习。现有的迁移学习在分类领域已有较多研究成果[2, 3, 4, 5, 6, 7, 8, 9, 10],而在聚类领域迁移学习理论和方法相对则要少很多。文献[11, 12]在聚类领域利用了迁移学习的理论。
半监督聚类是半监督学习与聚类分析相结合的研究领域,文献[13]提出了不同情况下的半监督聚类算法,并取得了不错的效果。
文献[14]将经典的模糊C均值算法[15](FCM)与可能性C均值[16](PCM)算法进行改进,提出了模糊可能性聚类算法(FPCM)。本文探讨在源领域有少量标签的情况下,如何指导目标域进行聚类,提出半监督模糊可能性C均值聚类算法(SS-FPCM),并针对负迁移问题对算法进行改进,提出了防止负迁移的半监督迁移算法(TSS-FPCM),同时,用代表点代替源领域的数据进行数据迁移,得到改善的半监督迁移算法(ITSS-FPCM),并进行了实验验证。
1 相关算法介绍 1.1 PCM聚类算法
PCM聚类算法放松了传统FCM聚类算法中对于隶属度矩阵的约束,隶属度不再是对1的共享。对于给定数据集
X={xk|k=1,2,…,N},xk∈Rd,包含N个样本,分成C个类别,T={tik|i=1,2,
…,C;k=1,2,…,N}是可能划分矩阵,tik表示第k个样本xk属于第i类的可能性,聚类中心为V={vi|i=1,2,…,C},其中vi表示第i个聚类中心。PCM目标函数定义为
$J = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {t_{_{ik}}^md_{ik}^2} } + \sum\limits_{i = 1}^C {{\eta _i}} \sum\limits_{k = 1}^N {{{\left( {1 - {t_{ik}}} \right)}^m}d_{ik}^2} $
(1)
dik2=‖xk-vi‖2=(xk-vi)T(xk-vi)
(2)
${\eta _i} = K\frac{{\sum\limits_{k = 1}^N {t_{_{ik}}^md_{ik}^2} }}{{\sum\limits_{k = 1}^N {t_{_{ik}}^m} }},K > 0$
(3)
最小化目标函数可以得到可能性矩阵和聚类中心的迭代式(4)和式(5):
${t_{ik}} = \frac{1}{{1 + {{\left( {\frac{{d_{ik}^2}}{{{\eta _i}}}} \right)}^{\frac{1}{{m - 1}}}}}},\forall i,k$
(4)
${\nu _i} = \frac{{\sum\limits_{k = 1}^N {t_{_{ik}}^m{x_k}} }}{{\sum\limits_{k = 1}^N {t_{_{ik}}^m} }},\forall i$
(5)
FPCM是建立在FCM和PCM基础上的算法,它将两者结合在一起 ,FPCM的目标函数定义为
$J = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {\left( {u_{_{ik}}^m + t_{_{ik}}^\eta } \right)d_{ik}^2} } $
(6)
$\sum\limits_{k = 1}^N {{t_{ik}}} = 1,\forall i$
(7)
$\sum\limits_{i = 1}^C {{u_{ik}}} = 1,\forall k$
(8)
通过最小化目标函数,可以得到以下迭代优化公式:
${u_{ik}} = {\left[ {\sum\limits_{j = 1}^C {{{\left( {\frac{{d_{ik}^2}}{{d_{ij}^2}}} \right)}^{\frac{1}{{m - 1}}}}} } \right]^{ - 1}},\forall i,k$
(9)
${t_{ik}} = {\left[ {\sum\limits_{j = 1}^N {{{\left( {\frac{{d_{ik}^2}}{{d_{ij}^2}}} \right)}^{\frac{1}{{\eta - 1}}}}} } \right]^{ - 1}},\forall i,k$
(10)
${\nu _i} = \frac{{\sum\limits_{k = 1}^N {\left( {u_{_{ik}}^m + t_{_{ik}}^\eta } \right){x_k}} }}{{\sum\limits_{k = 1}^N {\left( {u_{_{ik}}^m + t_{_{ik}}^\eta } \right)} }},\forall i$
(11)
对于一些有着一部分标签的数据集,在文献[17]中,Pedrycz提出了基于部分标签的模糊聚类算法(SS-FCM),算法的核心思想是利用现有的分类信息,并把它作为优化程序的一部分。
为了区分标记数据与未标记数据,引入向量矩阵
B={bk|k=1,2,…,N},如果xk是已知标签样本bk=1,否则bk=0。并且记类别属性F={fik|i=1,2,…,C;k=1,2,…,N},如果xk属于第i类,那么fik=1;否则fik=0。在引入
B和F后,Pedrycz将模糊参数m取值为2,其目标函数为
$J = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {u_{ik}^2d_{ik}^2} } + \alpha \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {{{\left( {{u_{ik}} - {f_{ik}}{b_k}} \right)}^2}d_{ik}^2} } $
(12)
对半监督FCM算法进行研究可以发现,上文中的
B和F的功能相似,保留下F并对FPCM的目标函数做如下改进:
$J = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)d_{ik}^2} } + \omega \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {{{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}d_{ik}^2} } $
(13)
s.t. α ≥ 0, β ≥ 0, ω > 0, 0 ≤ uik , tik ≤ 1
最小化目标函数,可以得到迭代表达式:
${t_{ik}} = {\left[ {\sum\limits_{j = 1}^N {\left( {\frac{{d_{ik}^2}}{{d_{ij}^2}}} \right)} } \right]^{ - 1}},\forall i,k$
(14)
${u_{ik}} = \frac{1}{{\alpha + \omega }}\frac{{\alpha + \omega \left( {1 - \sum\limits_{j = 1}^C {{f_{jk}}} } \right)}}{{\sum\limits_{j = 1}^C {\frac{{d_{ik}^2}}{{d_{ij}^2}}} }} + \omega {f_{jk}},\forall i,k$
(15)
${\nu _i} = \frac{{\sum\limits_{k = 1}^N {\left[ {\alpha u_{ik}^2 + \beta t_{ik}^2 + \omega {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right]} {x_k}}}{{\sum\limits_{k = 1}^N {\left[ {\alpha u_{ik}^2 + \beta t_{ik}^2 + \omega {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right]} }},\forall i$
(16)
通过不断迭代优化隶属度矩阵最终获得我们需要的划分。改进的半监督模糊可能性C均值算法(SS-FPCM)能够通过α、β控制FPCM中FCM和PCM的权重,通过参数ω的变化控制已知标签在算法中所占的比重。
2.2 历史标签数据的迁移迁移学习可以将历史场景(也叫源数据)中获取需要的数据或者信息,用于指导当前场景(又成为目标数据),当历史场景的信息与当前场景的相关性足够大时,可以从中得到潜藏的信息。在当历史场景没有任何指导信的数据(无任何标签信息)时,文献[11, 12]针对这种情况分别做出了自己的研究。
当源数据有少量的标签时候,可以很直观地想到,将这些数据提取出来,加入到当前场景,一起进行聚类,以期待能够指导当前场景。前面提到了半监督FPCM聚类算法能够有效利用标签进行聚类,便可以直接引用式(13)的目标函数。但是,在迁移学习中负迁移是难以避免的一个问题,如果历史场景与当前场景相关性并不大。那么历史数据的标签很可能对当前场景产生不良影响,造成负迁移现象。针对这个问题,对式(13)进行改造,提出避免负迁移的半监督迁移聚类算法(TSS-FPCM)。
假设历史场景中有M个已知标签样本,将数据提取放在目标数据的后面,构成新的目标数据集X′={xk|k=1,2,…,N,N+1,…,N+M},xk∈Rd,其中后M个数据为历史场景中的已知样本,根据数据集提出新的目标函数为
$\begin{gathered}
J = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)d_{ik}^2} } + \hfill \\
\omega \left[ {\sum\limits_{i = 1}^C {\sum\limits_{k = N + 1}^{N + M} {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)d_{ik}^2 + \sum\limits_{i = 1}^C {\sum\limits_{k = N + 1}^{N + M} {{{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}d_{ik}^2} } } } } \right] \hfill \\
{\text{s}}{\text{.t}}{\text{.}} \alpha ≥ 0,\beta ≥ 0,\omega > 0,0 ≤ {u_{ik}},{t_{ik}} ≤ 1 \hfill \\
\sum\limits_{i = 1}^C {{u_{ik}} = 1 \forall k,} \sum\limits_{k = 1}^{N + M} {{t_{ik}}} = 1 \forall i \hfill \\
\end{gathered} $
(17)
不直接使用式(13)的目标函数而改用式(17)的目标函数,当参数ω趋于0的时候,前者相当于将M个源数据当作未知标签加入到目标领域中进行无监督混合C均值聚类,而后者则等于认为这些数据没有用处而舍弃。可以发现前者无法控制加入源数据后所可能造成的负迁移现象影响聚类结果,而后者则可以有效避免该情况。
最小化目标函数可以得到:
${t_{ik}} = \left\{ \begin{gathered}
{\left( {\sum\limits_{j = 1}^N {\frac{{d_{ik}^2}}{{d_{ij}^2}}} + \sum\limits_{j = N + 1}^{N + M} {\frac{{d_{ik}^2}}{{\omega d_{ij}^2}}} } \right)^{ - 1}}, k ≤ N \hfill \\
{\left( {\sum\limits_{j = 1}^N {\frac{{\omega d_{ik}^2}}{{d_{ij}^2}}} + \sum\limits_{j = N + 1}^{N + M} {\frac{{d_{ik}^2}}{{d_{ij}^2}}} } \right)^{ - 1}}, N < k ≤ N + M \hfill \\
\end{gathered} \right.$
(18)
${u_{ik}} = \left\{ \begin{gathered}
{\left( {\sum\limits_{j = 1}^C {\frac{{d_{ik}^2}}{{d_{ij}^2}}} } \right)^{ - 1}}, k ≤ N \hfill \\
\frac{{1 - \frac{1}{{1 + \alpha }}\sum\limits_{j = 1}^C {{f_{jk}}} }}{{\sum\limits_{j = 1}^C {\frac{{d_{ik}^2}}{{d_{ij}^2}}} }} + \frac{1}{{1 + \alpha }}{f_{jk}}, N < k ≤ N + M \hfill \\
\end{gathered} \right.$
(19)
$\begin{gathered}
{v_i} = \hfill \\
\frac{{\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right){x_k} + \omega \sum\limits_{k = N + 1}^{N + M} {\left\{ {\alpha u_{ik}^2 + \beta t_{ik}^2 + {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right\}{x_k}} } }}{{\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right) + \omega \sum\limits_{k = N + 1}^{N + M} {\left\{ {\alpha u_{ik}^2 + \beta t_{ik}^2 + {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right\}{x_k}} } }},\forall i \hfill \\
\end{gathered} $
(20)
在历史场景中,除了少量的标签信息,还有大量的未标记数据,这些数据量远远大于已标记数据,同样可以从中获取需要的信息来帮助当前场景。直接将大量未标记数据加入当前场景中进行聚类大大增加了计算量。
在历史场景中,为了减少计算量,可以使用一个“代表点”来表示一个类,而不仅仅是文献[11]中的聚类中心;这个点既可以是聚类中心,也可以是数据中的真实样本点,将庞大的数据变为有限的几个点。
为了能够有效地利用“代表点”,给定代表点集合X${\hat X}$={${{\hat x}_i}$|i=1,2,…,C},C表示聚类个数,重新定义新的距离函数为
\[\mathop {d_{ik}^2}\limits^ \gg = {\left\| {{x_k} - {v_i}} \right\|^2} + {\gamma _1}{\left\| {{x_k} - {{\hat x}_i}} \right\|^2} + {\gamma _2}{\left\| {{v_i} - {{\hat x}_i}} \right\|^2}\]
(21)
\[\begin{gathered}
J = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)\mathop {d_{ik}^2}\limits^ \gg } } + \hfill \\
\omega \left\{ {\sum\limits_{i = 1}^C {\sum\limits_{k = N + 1}^{N + M} {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)\mathop {d_{ik}^2}\limits^ \gg } } + } \right. \hfill \\
\left. {\sum\limits_{i = 1}^C {\sum\limits_{k = N + 1}^{N + M} {{{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}\mathop {d_{ik}^2}\limits^ \gg } } } \right] \hfill \\
\end{gathered} \]
(22)
\[\begin{gathered}
Q = \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)\mathop {d_{ik}^2}\limits^ \gg } } + \hfill \\
\omega \left[ {\sum\limits_{i = 1}^C {\sum\limits_{k = N + 1}^{N + M} {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)\mathop {d_{ik}^2}\limits^ \gg } } + \sum\limits_{i = 1}^C {\sum\limits_{k = N + 1}^{N + M} {{{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}\mathop {d_{ik}^2}\limits^ \gg } } } \right] + \hfill \\
\sum\limits_{k = 1}^{N + M} {{\lambda _k}\left( {1 - \sum\limits_{i = 1}^C {{u_{ik}}} } \right)} + \sum\limits_{i = 1}^C {{\theta _i}\left( {1 - \sum\limits_{i = 1}^{N + M} {{t_{ik}}} } \right)} \hfill \\
\end{gathered} \]
(23)
令∂Q/∂Vi=0,解得:
\[\begin{gathered}
{\upsilon _i} = \hfill \\
\frac{{\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right){x_k}} + {\gamma _2}\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right){{\hat x}_i}} + \omega \left[ {\sum\limits_{k = N + 1}^{N + M} {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2 + {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right){x_k}} + {\gamma _2}\sum\limits_{k = N + 1}^{N + M} {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2 + {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right){{\hat x}_i}} } \right]}}{{\left( {1 + {\gamma _2}} \right)\left[ {\sum\limits_{k = 1}^N {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2} \right)} + \omega \sum\limits_{k = N + 1}^{N + M} {\left( {\alpha u_{ik}^2 + \beta t_{ik}^2 + {{\left( {{u_{ik}} - {f_{ik}}} \right)}^2}} \right)} } \right]}} \hfill \\
\end{gathered} \]
(24)
令∂Q/∂λk=0,可以得到:
\[\sum\limits_{i = 1}^C {{u_{ik}}} = 1\]
(25)
令∂Q/∂uik=0,对于0<k≤N可以解得:
\[{u_{ik}} = \frac{\lambda }{{2\alpha \mathop {d_{ik}^2}\limits^ \gg }}\]
(26)
将式(26)代入式(25),解得:
\[\frac{\lambda }{{2\alpha }} = {\left( {\sum\limits_{i = 1}^C {\frac{1}{{\mathop {d_{ik}^2}\limits^ \gg }}} } \right)^{ - 1}}\]
(27)
再将λ代回式(26),得到:
\[{u_{ik}} = {\left( {\sum\limits_{j = 1}^C {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{jk}^2}\limits^ \gg }}} } \right)^{ - 1}}\]
(28)
同理,对于N<k≤N+M,可以求出:
\[{u_{ik}} = \frac{{1 - \frac{1}{{1 + \alpha }}\sum\limits_{j = 1}^C {{f_{jk}}} }}{{\sum\limits_{j = 1}^C {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{jk}^2}\limits^ \gg }}} }} + \frac{1}{{1 + \alpha }}{f_{jk}}\]
(29)
合并式(28)和(29)可以得到最终表达式:
\[{u_{ik}} = \left\{ {\begin{array}{*{20}{l}}
{{{\left( {\sum\limits_{j = 1}^C {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{jk}^2}\limits^ \gg }}} } \right)}^{ - 1}},}&{k ≤ N} \\
{\frac{{1 - \frac{1}{{1 + \alpha }}\sum\limits_{j = 1}^C {{f_{jk}}} }}{{\sum\limits_{j = 1}^C {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{jk}^2}\limits^ \gg }}} }} + 1 - \frac{1}{{1 + \alpha }}{f_{jk}},}&{N < k ≤ N + M}
\end{array}} \right.\]
(30)
使用同样得方法,可以求得tik的迭代表达式:
\[{t_{ik}} = \left\{ {\begin{array}{*{20}{c}}
{{{\left( {\sum\limits_{j = 1}^N {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{ij}^2}\limits^ \gg }}} + \sum\limits_{j = N + 1}^{N + M} {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\omega \mathop {d_{ij}^2}\limits^ \gg }}} } \right)}^{ - 1}},}&{k ≤ N} \\
{{{\left( {\sum\limits_{j = 1}^N {\frac{{\omega \mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{ij}^2}\limits^ \gg }}} + \sum\limits_{j = N + 1}^{N + M} {\frac{{\mathop {d_{ik}^2}\limits^ \gg }}{{\mathop {d_{ij}^2}\limits^ \gg }}} } \right)}^{ - 1}},}&{N < k ≤ N + M}
\end{array}} \right.\]
(31)
根据上一节的公式,ITSS-FPCM的表述如下:
算法1 ITSS-FPCM算法
输入 前N个数据样本为目标数据,后M个为已知标签的历史数据的数据样本X′={xk|k=1,2,…,N,N+1,…,N+M},聚类个数C,最大迭代次数L,当前迭代次数l=1,源数据类代表点${\hat X}$,相关参数α、β、ω、γ1和γ2,阈值ε。
输出 聚类中心 vi,隶属度矩阵uik和概率矩阵tik。
1)初始化聚类中心vi,根据已知标签构造矩阵 F,初始化目标函数J(l)=0。
2)根据表达式(30)更新vik。
3)根据表达式(31)更新vik。
4)根据表达式(24)更新vi。
5)l=l+1,计算新的目标函数J(l),如果J(l)-J(l-1)<ε,或者l>L跳到第6),否则,跳到2)。
6)聚类中心vi,隶属度矩阵vik和概率矩阵vik。
3 实验结果为了验证算法的有效性,实验使用了人工数据集、UCI真实数据集以及文本数据集进行相关的实验验证。
在进行聚类结果评价时,选取了相关的4种聚类评价指标:正确率AC(Accuracy)[18]、归一化互信息NMI(normalized mutual information)[11, 18]、芮氏指标RI(Rand Index)[11, 19] 和F-measure[19]。 4个指标的值域均在0到1,值越大表示聚类质量越好。
实验中选取了LSSMTC[18]、Co-Clustering[20]、FPCM、TSC[12]、T-GIFP-FCM[11]算法进行对比实实验;评价结果将进行10次计算取平均值。
3.1 人工数据集为了模拟源场景和当前目标场景,实验使用文献[11]的方法:首先利用高斯函数生成相关的数据集,随机生成类别数为3,每类250个样本点,每个样本点为两微的源场景数据,如图 1所示。
 |
| 图 1 源数据Fig. 1 Source Dataset |
如图 2所示,同样利用高斯分布函数产生当前数据集Set1和Set2 两个数据集;其中Set1每类样本数目为20,如图 2(a)所示;Set2每类样本数目为100,再向其中加入高斯噪声构成,如图 2(b)所示。
 |
| 图 2 目标数据集Fig. 2 Target dataset |
两个数据集分别模拟当前的数据样本信息匮乏(数据不足)、充足(数据足够)但是受污染(有噪声)的不同情况下进行聚类。
实验时,SS-FPCM,TSS-FPCM,ITSS-FPCM算法需要已知部分源标签,随机从源数据中抽取3%的样本作为已知标签数据进行实验,实验结果如表 1所示,表格中“—”表示该数据集不满足算法运行的基本条件。
| 数据集 | 评价指标 |
|
| Set1 |
| ||||||||||||||||||||||||||||||||||||
| Set2 |
|
从表 1可以看出:
1)在Set1数据集中样本量很少,少量的源标签数据样本和其他信息都能够对目标数据产生正向的推动作用,从而达到较好的结果,SS-FPCM与TSS-FPCM的结果验证了这一点;T-GITP-FCM算法也可以得到很好的结果;
2)在有噪声的数据集Set2上,少量的标签不足以取得令人满意的效果,仍需要源数据的其他帮助,SS-FPCM与TSS-FPCM算法的结果不如T-GIFP-FCM算法;说明SS-FPCM与TSS-FPCM算法在抗干扰方面存在不足;
3)改进后的ITSS-FPCM算法则在Set1和Set2上均取得了良好的聚类效果。说明当在数据信息不足,数据样本有限,数据受污染的时候,在有大量历史数据的帮助下迁移算法可以取得不错的效果,改进的ITSS-FPCM算法在抗噪声和干扰方面优于其他算法。
3.2 UCI真实数据集UCI中的Image Segment Data Set是一个图片数据集,它由7个室外图像数据库中随机抽取,组成7个不同的类别,共2 100个样本数据,其中每个类别含有300个样本点。 实验从数据中抽取70%的数据作为源数据,剩下的构成目标数据进行实验,数据构成如表 2。
| 数据类型 | 样本数 | 维数 | 类别 |
| 源数据 | 1 470 | 19 | 7 |
| 目标数据 | 630 | 19 | 7 |
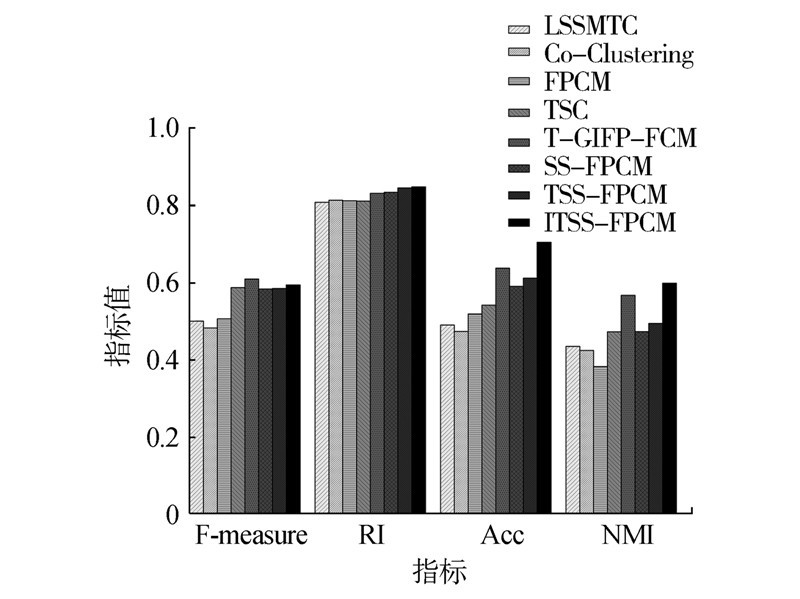
算法在数据集的聚类结果如图 3所示,从图中可以发现本文所提出的ITSS-FPCM算法在4个指标均取得了不错的结果,在准确率与NMI指标上有相对较大的优势,进一步验证了算法得有效性。
|
| 图 3 8个算法在Image Segment数据集上的对比 Fig. 3 Comparison of 8 algorithms on image segment data set |
20NG(20Newsgroups)[12]是一个真实的新闻文本数据集,数据集收集了大约2万条新闻组,均匀地分布到20个不同的集合中,20个小集合又可以分为4个大的类别,该数据集在大量迁移学习分类算法中被使用。
TDT2[21](NIST话题检测与跟踪的语料库)共收集1998年上半年6个来源的数据,包含2个通讯社(APW,NYT),2个电台节目(VOA,PRI)和2个电视节目(CNN,ABC),共1万多个样本数据。
Reuters-21578[21]语料库包含21 578个文件,放在135个文件夹下。
实验时分别对3个文本数据集抽取其中一部分类别,利用工具进行降维处理后构成新的数据集样本,数据具体构成如表 3所示。
| 数据来源 | 数据类型 | 样本数 | 维数 | 类别 |
| comp vs sci(20NG) | 源数据 | 1 200 | 400 | 2 |
| 目标数据 | 400 | 400 | 2 | |
| rec vs talk(20NG) | 源数据 | 1 200 | 400 | 2 |
| 目标数据 | 400 | 400 | 2 | |
| TDT2 | 源数据 | 1 800 | 400 | 6 |
| 目标数据 | 600 | 400 | 6 | |
| Reuters-21578 | 源数据 | 800 | 400 | 4 |
| 目标数据 | 400 | 400 | 4 |
聚类的结果如表 4所示,结果中可以看到:
1) 利用迁移学习的TSC、T-GIFP-FCM、TSS-FCM、ITSS-FCM算法在效果上均优于非迁移学习型算法,表明迁移学习能够有效地提升聚类的性能;
2)仅对源数据少量标签数据直接使用的SS-FPCM算法和TSS-FPCM算法对当前场景的作用有限,不及能够利用更多信息的TSC迁移聚类和T-GIFP-FCM算法,但还是能够有效地提高聚类性能;
3) 本论文的ITSS-FPCM算法在大部分指标都优于其他算法,但是当源数据与目标数据相关性不大时,基于标签与代表点的直接迁移对当前场景帮助有限,不及STC算法的聚类效果,存在着局限性和适用范围的问题。
| 数据集 | 评价指标 | 算法 | |||||||
| LSSMTC | Co-Clustering | FPCM | TSC | T-GIFP-FCM | SS-FPCM | TSS-FPCM | ITSS-FPCM | ||
| sciSet1 | F-measure | 0.683 4 | 0.664 8 | 0.633 1 | 0.768 8 | 0.695 6 | 0.698 4 | 0.718 7 | 0.733 6 |
| RI | 0.558 5 | 0.555 0 | 0.524 1 | 0.645 0 | 0.577 0 | 0.575 0 | 0.595 8 | 0.609 5 | |
| AC | 0.816 5 | 0.667 5 | 0.750 0 | 0.770 0 | 0.697 5 | 0.695 0 | 0.720 0 | 0.735 0 | |
| NMI | 0.134 1 | 0.102 1 | 0.118 9 | 0.292 3 | 0.148 3 | 0.109 8 | 0.134 2 | 0.156 4 | |
| rec vs talk | F-measure | 0.686 7 | 0.639 4 | 0.698 0 | 0.882 7 | 0.890 7 | 0.831 1 | 0.846 9 | 0.915 8 |
| RI | 0.580 3 | 0.539 5 | 0.576 9 | 0.792 1 | 0.803 7 | 0.720 4 | 0.740 9 | 0.844 0 | |
| AC | 0.705 3 | 0.642 5 | 0.697 5 | 0.882 5 | 0.890 0 | 0.832 5 | 0.847 5 | 0.915 0 | |
| NMI | 0.176 9 | 0.087 1 | 0.0993 | 0.463 7 | 0.487 3 | 0.349 2 | 0.375 0 | 0.574 8 | |
| TDT2 | F-measure | 0.6427 | 0.613 9 | 0.478 7 | 0.855 4 | 0.8897 | 0.821 4 | 0.825 3 | 0.885 8 |
| RI | 0.782 8 | 0.747 3 | 0.682 5 | 0.907 0 | 0.9299 | 0.884 5 | 0.888 4 | 0.930 0 | |
| AC | 0.698 3 | 0.713 3 | 0.608 3 | 0.863 3 | 0.8967 | 0.833 3 | 0.835 0 | 0.888 3 | |
| NMI | 0.542 6 | 0.575 0 | 0.398 0 | 0.753 5 | 0.8093 | 0.719 9 | 0.721 7 | 0.829 8 | |
| Reuters-21578 | F-measure | 0.710 1 | 0.684 0 | 0.6361 | 0.824 7 | 0.8533 | 0.812 1 | 0.817 8 | 0.860 8 |
| RI | 0.812 5 | 0.715 3 | 0.6620 | 0.841 9 | 0.8658 | 0.832 3 | 0.837 6 | 0.870 9 | |
| AC | 0.820 0 | 0.727 5 | 0.719 1 | 0.830 0 | 0.8550 | 0.815 0 | 0.820 0 | 0.865 0 | |
| NMI | 0.566 2 | 0.505 2 | 0.448 5 | 0.659 0 | 0.6430 | 0.616 2 | 0.624 2 | 0.707 6 | |
本文将半监督学习思想应用到FPCM算法上,提出半监督SS-FPCM算法;迁移学习方面对算法进行非负迁移改进,得到TSS-FPCM算法,再利用“代表点”代替原始数据提出了改进的半监督的迁移聚类算法ITSS-FPCM。在多种数据集上的实验验证表明,ITSS-FPCM算法在性能上要好于SS-FPCM算法与TSS-FPCM算法。在数据量不足、数据被污染的情况下,ITSS-FPCM算法能够提升聚类的性能;算法在源数据与目标数据相关不大时效果一般,下一步研究将会提取其他相关信息改善聚类性能,同时考虑参数的优化问题。
| [1] | 庄福振, 罗平, 何清, 等. 迁移学习研究进展[J]. 软件学报, 2015, 26(1): 26-39. ZHUANG Fuzhen, LUO Ping, HE Qing, et al. Survey on transfer learning research[J]. Journal of software, 2015, 26(1): 26-39. |
| [2] | WEI Fengmei, ZHANG Jianpei, CHU Yan, et al. FSFP: transfer learning from long texts to the short[J]. Applied mathematics and information sciences, 2014, 8(4): 2033-2040. |
| [3] | DAI Wenyuan, XUE Guirong, YANG Qiang, et al. Co-clustering based classification for out-of-domain documents[C]//Proceedings of the 13th ACM SIGKDD Tinternational Conference on Knowledge Discovery and Data Mining. San Jose, California, USA, 2007: 210-219. |
| [4] | DAI Wenyuan, YANG Qiang, XUE Guirong, et al. Self-taught clustering[C]//Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland,, 2008: 200-207. |
| [5] | SAMANTA S, SELVAN A T, DAS S. Cross-domain clustering performed by transfer of knowledge across domains[C]//Proceedings of the 4th National Conference on Pattern Recognition, Image Processing and Graphics (NCVPRIPG). Jodhpur, India, 2013: 1-4. |
| [6] | DAI Wenyuan, XUE Guirong, YANG Qiang, et al. Transferring naive Bayes classifiers for text classification[C]//Proceedings of the 22nd National Conference on Artificial Intelligence. Vancourver, British Columbia, Canada, 2007, 1: 540-545. |
| [7] | LIAO Xuejun, XUE Ya, CARIN L. Logistic regression with an auxiliary data source[C]//Proceedings of the 22nd International Conference on Machine Learning. New York, NY, USA, 2005: 505-512. |
| [8] | DAI Wenyuan, YANG Qiang, XUE Guirong, et al. Boosting for transfer learning[C]//Proceedings of the 24th International Conference on Machine Learning. Corvallis, Oregon, USA, 2007: 193-200. |
| [9] | LUO Ping, ZHUANG Fuzhen, XIONG Hui, et al. Transfer learning from multiple source domains via consensus regularization[C]//Proceedings of the 17th ACM Conference on Information and Knowledge Management. Napa Valley, California, USA, 2008: 103-112. |
| [10] | DUAN Lixin, TSANG I W, XU Dong, et al. Domain adaptation from multiple sources via auxiliary classifiers[C]//Proceedings of the 26th Annual International Conference on Machine Learning. Montreal, Canada,, 2009: 289-296. |
| [11] | 蒋亦樟, 邓赵红, 王骏, 等. 基于知识利用的迁移学习一般化增强模糊划分聚类算法[J]. 模式识别与人工智能, 2013, 26(10): 975-984. JIANG Yizhang, DENG Zhaohong, WANG Jun, et al. Transfer generalized fuzzy c-means clustering algorithm with improved fuzzy partitions by leveraging knowledge[J]. Pattern recognition and artificial intelligence, 2013, 26(10): 975-984. |
| [12] | JIANG Wenhao, CHUNG F L. Transfer spectral clustering[M]//FLACH P A, DE BIE T, CRISTIANINI N. Machine learning and knowledge discovery in databases: lecture notes in computer science. Berlin Heidelberg: Springer, 2012, 7524: 789-803. |
| [13] | 李昆仑, 曹铮, 曹丽苹, 等. 半监督聚类的若干新进展[J]. 模式识别与人工智能, 2009, 22(5): 735-742. LI Kunlun, CAO Zheng, CAO Liping, et al. Some developments on semi-supervised clustering[J]. Pattern recognition and artificial intelligence, 2009, 22(5): 735-742. |
| [14] | PAL N R, PAL K, BEZDEK J C. A mixed c-means clustering model[C]//Proceedings of the 6th IEEE International Conference on Fuzzy Systems. Barcelona, Spain, 1997, 1: 11-21. |
| [15] | BEZDEK J C, EHRLICH R, FULL W. FCM: The fuzzy c-means clustering algorithm[J]. Computers and geosciences, 1984, 10(2-3): 191-203. |
| [16] | KRISHNAPURAM R, KELLER J M. The possibilistic C-means algorithm: insights and recommendations[J]. IEEE transactions on fuzzy systems, 1996, 4(3): 385-393. |
| [17] | PEDRYCZ W. Algorithms of fuzzy clustering with partial supervision[J]. Pattern recognition letters, 1985, 3(1): 13-20. |
| [18] | GU Quanquan, ZHOU Jie. Learning the shared subspace for multi-task clustering and transductive transfer classification[C]//Proceedings of the 2009 9th IEEE international conference on data mining. Miami, Florida, USA, 2009: 159-168. |
| [19] | 杨燕, 靳蕃, KAME M. 聚类有效性评价综述[J]. 计算机应用研究, 2008, 25(6): 1630-1632, 1638. YANG Yan, JIN Fan, KAME M. Survey of clustering validity evaluation[J]. Application research of computers, 2008, 25(6): 1630-1632, 1638. |
| [20] | GU Quanquan, ZHOU Jie. Co-clustering on manifolds[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France, 2009: 359-368. |
| [21] | CAI Deng, HE Xiaofei, HAN Jiawei. Locally consistent concept factorization for document clustering[J]. IEEE transactions on knowledge and data engineering, 2011, 23(6): 902-913. |



