随着获得的数据越来越多,利用机器学习、数据挖掘[1, 2, 3]等手段从数据中获取潜在的知识变得越来越重要。然而如何评估挖掘出来的信息,即评估数据挖掘结果的质量是一个十分重要的问题。只有一个好的评估方法,才能保证挖掘算法发现高质量的信息。聚类[4, 5]是数据挖掘领域一个很重要的分支。同时,聚类的应用也越来越广泛。随着聚类的广泛应用,如何有效地评估聚类结果的质量[6, 7]成为一个重要的研究课题。虽然评估聚类结果的重要性一点不亚于挖掘算法本身,但是评估方面却没有受到它应有的重视。
针对聚类,现有的方法主要是用评价函数对聚类结果评估。这种函数一般分3种类型:紧密型、分散型和连接型。常见的评估函数有DB-Index, Sihouette-Index, Dunn-Index等。这些函数能够评估聚类结果,但是这些函数评估出来的结果往往没有一个比较好的可以参考的值。即一个评估值计算出来之后得到的只是一个评估值,至于这个值达到什么标准能够接受并不能确定。利用统计方法评估聚类结果的算法很少,其主要原因是聚类的特殊性与复杂性使传统的统计方法很难用到聚类质量评估上。近年来有一些利用随机方法来评估聚类结果的研究,但也存在一定的问题。本文根据存在的问题提出了一种基于置换检验的评估方法。
1 相关研究 1.1 利用簇结构评估聚类质量该方法先对原始数据聚类,然后将原始数据集按照一定的约束随机置换抽样构造新的数据集。抽样之后用同样的聚类算法对样本数据集进行聚类。这样重复大量的次数后,再用评估函数(如DB-Index)计算每个样本的函数值。如果原始数据集聚类结果的函数值小于大部分随机构造的数据集聚类结果的函数值,那么说明挖掘出来的信息是可靠的,否则说明聚类结果不可靠。更通俗一点,如果原来数据集没有好的簇结构,那么无论怎么聚类,结果都是不好的。代表性的方法有最大熵模型抽样[8]、矩阵元素交换[9]等。利用数据集簇结构来评估聚类质量[10]的方法能很好地评估出簇结构不好的聚类结果。实验证实对不同数据集进行聚类,有明显簇结构数据集的p-value会比没有明显簇结构的p-value小很多。但是这种方法并不能准确评估聚类的质量。从某种意义上讲,这种方法更适合评估一个数据集是否有好的簇结构。
1.2 SigClustSigClust[11]认为如果一个数据集符合高斯分布,那么对这个数据集的任何分割都是不合理的。因此这个方法的前提假设是:一个单一的簇的元素符合高斯分布。SigClust主要是针对k=2的聚类评估。对于k>2的情况,还没有比较好的解决办法。
1.3 层次聚类的p-value计算这种方法主要针对层次聚类的评估[12, 13]。层次聚类后会形成一个二叉树。对二叉树上的每个节点都进行置换检验,算出每个节点划分对应的p-value。这种算法的空假设为:当前节点的左子树和右子树应该属于一个簇。如果算出p-value 足够小就说明空假设是一个小概率事件,应该拒绝。该方法是将当前节点的左子树和右子树打乱,按照一定的约束随机分配左子树和右子树的元素。抽样若干次后形成的随机样本集按照某种指标与原始划分对比计算出p-value。这个评估只能针对层次聚类,不能对其他的聚类算法进行评估。另外这样计算出的p-value只是每个节点上的p-value, 并不是全局聚类的p-value。
2 基本概念 2.1 无监督聚类质量评估函数如果数据集中的元素没有类标签,聚类结果的评价就只能依赖数据集自身的特征和量值。在这种情况下,聚类的度量追求有3个目标:紧密度、分离度和链接度。
紧密度 簇中的每个元素应该彼此尽可能接近。紧密度的常用度量是方差,方差越小说明紧密度越大。
分离度 簇与簇之间应该充分分离。有3种常用方法来度量两个不同簇之间的距离。单连接:度量不同簇的两个最近成员的距离。全连接:度量不同簇的两个最远成员的距离。质心比较:度量不同簇的中心点的距离。
链接度 链接度指簇中的元素成员至少要跟同一个簇内的元素比较像。这个可以用来评估簇模型不是圆形或者球形的聚类结果,比如DBSCAN的聚类结果。
本文用一种无监督评估聚类质量的方法, Davies-Bouldin Index,即DB_Index。
${\text{DBI}} = \frac{1}{k}\sum\limits_{i = 1}^k {\max \left( {\frac{{{S_i} + {S_j}}}{{{D_{ij}}}}} \right)} .$
DBI的思想是一个高质量的聚类结果需要满足:同一个簇的各元素间相似度大,不同类之间的相似度小。在DBI中,分子越小意味着簇内元素相似度越大,分母越大意味着簇间相似度越小。
2.2 聚类评估的p-value
给一个数据集X,用DB-Index计算聚类结果的函数值为x0x0。数据集X所有可能的聚类结果的函数值为x1, x2, …xNall。置换检验的p-value定义为
${P_{perm}} = \frac{{\sum\nolimits_{n = 1}^{{N_{{\text{all}}}}} {I\left( {{x_n} ≤ {x_0}} \right)} }}{{{N_{{\text{all}}}}}}$
${P_{perm0}} = \frac{{\sum\nolimits_{n = 1}^N {I\left( {{x_n} ≤ {x_0}} \right)} }}{N}.$
${P_{perm1}} = \frac{{1 + \sum\nolimits_{n = 1}^N {1\left( {{x_n} ≤ {x_0}} \right)} }}{{N + 1}}$
这种方法把分子加1的理由是把x0也看作置换检验一个样本的函数值。这就避免了得到p-value为0的试验结果。然而这种做法事实上是不太合理的。试想如果抽样999次没有发现比x0更小的统计值,这样草率地得出结论当前置换检验的结果为0.001显然太武断了。因为可能抽样99 999次依旧没有比x0更优的样本。那么依照这个计算公式p-value又为0.000 01。而实际上p-value的值可能更小。因此本文把p-value的定义为Pperm0Pecdf0。
置换检验的准确性取决于抽样的数目,一般的置换检验抽样的次数都在1 000次以上。为了得到更精确的p-value抽样的次数越多越好,理想的情况是置换所有的可能。然而对于不同的数据集合,甚至很难预测需要执行多少次置换才能够得到比较好的结果。往往为了得到更精确的值就会增大抽样次数,但是增加抽样次数的代价是增加计算的复杂性。对于普通的数据集往往抽样次数达到10 000次之后就不太容易提高抽样次数。而这样做又产生出了一个问题。如果一个聚类结果真实的p-value为0.000 001。而抽样的次数只有10 000次的话,那么p-value为就为0了。针对这些问题,本文提出了一种新的聚类评估方法,ECP,该方法能比较好地解决上文提到的问题。
3 基于置换检验的聚类结果评估 3.1 基本思想本文提出的置换检验方法将关注点锁定在了聚类的结果上。评估聚类结果的本质是看聚类算法对数据集中元素的划分质量。从这个角度出发,可以枚举对数据集的划分,然后用评估函数算出枚举划分的函数值。如果绝大部分划分都没有要评估的聚类结果质量好的话,那么就说明要评估的聚类结果质量比较好。相反地,就说明要评估的聚类结果质量并不好。
因此对于一个聚类结果,本文定义了零假H0: 当前聚类结果不是一个高质量的聚类。然后计算这个零假设的p-value。如果这个p-value非常小,就认为这个划分结果可以接受,可以拒绝H0。否则认为这个聚类结果不能接受。
定义数据集X是一个包含n个元素的d维数值型矩阵。首先对数据集聚类,聚成k簇后每个元素都会归属于一个簇。我们对每个簇进行标号。标号从0开始,往后依次是1, 2, …, k-1。定义CIi为第i个元素所属的簇标号。比如CI3=2表示第3个元素属于标号为2的簇。
接下来是抽样。抽样要满足一定约束。本文定义的约束是: 样本中簇包含元素的数目要与待评估聚类结果中簇中元素的数目保持一致。举个例子,假设数据集元素数目n为 100。划分成3簇,划分簇中的数目分别是40、33、27。那么抽样出来的样本也要满足这些条件,也就是要划分成3簇,并且簇中元素的数目也必须是40、33、27。具体的抽样方法: 首先搜集所有元素的簇标号,然后将这些簇标号随机地分配给每个元素。其实这个过程是洗牌算法。算法1描述了抽样的过程。
算法1 Shuffle(CI, n)
for i← 0 to n-1 do
index ← rand() mod (i + 1)
swap(CIi, CIindexCIi, CIindex)
可以用数学归纳法进行证明算法1保证了每个元素获得同一簇标号的概率是一样的。抽样的复杂度为O(n)。这样进行抽样N次,就得到了N个样本。然后利用样本对原始聚类结果进行评估。用DB-Index算出原始聚类的函数值x0与样本的函数值x1, x2, …,xN。有了这些值就能计算p-value了。具体算法如下。
算法2 ECP1
用DB-Index计算聚类结果的函数值x0。
for i ← 1 to N do
Shuffle(CI, n)
用DB-Index计算样本的函数值xi
计算p-value
一般情况下k$ \ll $n,因此 DB-Index的复杂度为O(n×d)。抽样一次的复杂度是O(n),容易算出总体复杂度为O(N×n×d)。这个复杂度还是比较高的。所以需要想一些方法来降低复杂度。N是抽样次数,期望越大越好。可以看到DB-Index是影响复杂度的主要因素。如果降低DB-Index计算的复杂性,那么就可以在相同的时间内抽取更多的样本来提高p-value的准确度。本文发现了DB-Index公式的特点,对上文提到的算法做了改进。
3.2 加速技巧首先选取聚类结果作为初始状态。然后随机交换一对簇标号不同的元素的簇标号。交换后把此时的划分作为一个样本,直接计算DB-Index的函数值。接下来继续交换一对簇标号不同的元素的簇标号,交换后计算DB-Index的值。这样迭代N次后就会得到N个样本的函数值。利用这N个值就可以计算出p-value。整个算法流程如下。
算法3 ECP2
用DB-Index计算聚类结果的函数值x0
for i← 1 to N do
随机交换一对簇标号不同元素的簇标号
用DB-Index计算抽样结果的函数值 xi
计算p-value
对比ECP1,ECP2只是修改了第3步的抽样方法。为什么修改了抽样方法就可以增大抽样次数?下面将仔细讨论DB-Index的计算过程。DB-Index的计算公式为
${\text{DBI}} = \frac{1}{k}\sum\limits_{i = 1}^k {\max \left( {\frac{{{S_i} + {S_j}}}{{{D_{ij}}}}} \right)} .$
${S_i} = \sqrt {\frac{{\sum\nolimits_{j = 1}^{{m_i}} {{{\left\| {{z_j} - \bar z} \right\|}^2}} }}{{{m_i}}}} .$
$\sum\nolimits_{j = 1}^{{m_i}} {{{\left\| {{z_j} - \bar z} \right\|}^2}} = \sum\nolimits_{t = 1}^d {\sum\nolimits_{j = 1}^{{m_i}} {{{\left( {{a_{jt}} - {{\bar a}_t}} \right)}^2}} } , $
$\begin{gathered}
\frac{{\sum\nolimits_{j = 1}^{{m_i}} {{{\left\| {{z_j} - \bar z} \right\|}^2}} }}{{{m_i}}} = \frac{{\sum\nolimits_{t = 1}^d {\sum\nolimits_{j = 1}^{{m_i}} {{{\left( {{a_{jt}} - {{\bar a}_t}} \right)}^2}} } }}{{{m_i}}} = \hfill \\
\sum\nolimits_{t = 1}^d {\frac{{\sum\nolimits_{j = 1}^{{m_i}} {{{\left( {{a_{jt}} - {{\bar a}_t}} \right)}^2}} }}{{{m_i}}}} \hfill \\
\end{gathered} $
$\frac{{\sum\nolimits_{j = 1}^{{m_i}} {{{\left( {{a_{jt}} - {{\bar a}_t}} \right)}^2}} }}{{{m_i}}} = \frac{{\sum\nolimits_{j = 1}^{{m_i}} {{a_{jt}}^2} }}{{{m_i}}} - {{\bar a}_t}^2$
$\frac{{\sum\nolimits_{j = 1}^{{m_i}} {{{\left\| {{z_j} - \bar z} \right\|}^2}} }}{{{m_i}}} = \sum\nolimits_{t = 1}^d {\frac{{\sum\nolimits_{j = 1}^{{m_i}} {{a_{jt}}^2} }}{{{m_i}}}} - {{\bar a}_t}^2$
${\sum\nolimits_{j = 1}^{{m_i}} {{a_{jt}}^2} }$是簇i中所有元素中第t维的平方和,${{\bar a}_t}$是簇i中所有元素第t维的平均值。所以为了计算Si,每一维只需要维护两个值就可以了:平方和与平均值。当簇标号交换的话,能在O(1)复杂度内修正这两个值。修改完每个维度的这两个值后,就可以用DB-Index算出函数值了。
可以看出修改一个簇的平方和与平均值复杂度是O(d)的。因此DB-Index的计算复杂度就是O(k×k×d)了。没有加速的DB-Index的计算复杂度是O(n×d)。一般情况下,k$ \ll $n。所以这种方法的效率有明显的提升。
3.3 更准确的p-value上边提到计算DB-Index的方法的复杂度为O(k×k×d)。虽然相比于原先的计算方法已经优化很多,但是对于p-value非常小的情况,可能依旧由于抽样数目有限而无法算出精确的p-value。这种情况下算出的p-value就会为0,然而这样的结果是不准确的。
如果知道了样本DB-Index函数值的概率分布就可以根据原始聚类结果的函数值算出精确的p-value了[14]。聚类是一种半监督的机器学习,其本质对元素所属类别的划分。如果对元素随机划分无穷次。那么质量特别高的划分的比例会很小。同样的,质量极端差的划分占的比例也会很小。很大比重的划分都介于它们之间。而正态分布的特点是:极端概率很小,中间的概率很大。经过对数据的分析,聚类划分的DB-Index函数值比较符合正态分布。因此可以假设抽样样本DB-Index的函数值符合正态分布。实际上正态分布符合很多自然概率分布的指标。下面要做的就是得到正态分布的参数。对于一维的正态分布均值和方差用式(1)和(2)得到:
$\mu = \frac{{\sum\nolimits_{i = 1}^N {{x_i}} }}{N}$
(1)
$\partial = \sqrt {\frac{{{{\left( {{x_i} - \bar x} \right)}^2}}}{{N - 1}}} $
(2)
有了概率分布函数,就能将原始聚类结果x0代入概率分布算出p-value了。
这样估出概率分布函数实现了在整体复杂度没有增加的前提下用较少的抽样得到更为精确p-value的目的了。
本文利用公式Pperm0$\frac{{\sum\limits_{n = 1}^N {I\left( {{y_n} > {x_0}} \right)} }}{N}$计算p-value实际上是利用了大数定律。大数定律的本质是如果有无穷次试验,事件出现的频率就会无限趋近于事件发生的概率。而由于抽样次数有限,本文假设了DB-Index的函数值符合正态分布。不过对于抽样N次后发现,已经有足够的样本可以精确算出p-value的话,就不需要用正态分布计算了。然而如果抽样N次后没有足够的样本可以用大数定律精确地计算p-value的话就要拟合正态概率分布函数了。对于有多少个样本满足xi≤x0算是足够呢?这是一个阈值问题。上边的过程总结起来如算法4。
算法4 ECP
抽样N次,算出每次的函数值xi
统计xi≤x0的数目M
如果M≥Limit利用公式Pperm0计算p-value
否则,拟合正态概率分布算出p-value
其中Limit是ECP的一个参数,是用Pperm0计算出p-value的最低数目限制。ECP不同于很多其他的置换检验方法。这种方法实现了用较少的抽样计算出更为精确p-value的目的,在效率上有了非常大的飞跃。
4 实验实验选取了iris、wine和yeast等3个数据集。这3个数据集都来自UCI数据库[15]。iris、wine和yeast数据集的属性都是数值型的,并且这3个数据集都带有类标签。
4.1 利用p-value选择合适的聚类算法从聚类这个概念提出以来出现了很多聚类算法。对于一个具体的应用,选择合适的聚类算法是一个很重要的问题。本文认为对于同一个数据集用不同的算法聚类,p-value小的那个结果更为可靠。为此本文对同一数据集选用多种算法聚类来验证p-value对选择聚类算法的有效性。实验结果如表 1。从实验结果可以看出,对于同一数据集p-value小的聚类算法对应的f-score和accuracy比较大。这说明利用p-value选择聚类算法是可靠的。本文还计算了p-value与f-score和accuracy的相关系数。本文用k-means对同一数据集聚类100次。通过控制k-means 的迭代次数来控制划分的质量。这样就避免了正常k-means聚类只会出现若干个固定情况的问题。
| 数据 | 算法 | p-value | f-score | accuracy |
| Iris | Random | 0.456 254 | 1.134 140 | 0.380 000 |
| Hierarchical Clustering | 0.100 548 | 1.656 570 | 0.666 667 | |
| DBSCAN | 0.042 825 | 2.714 400 | 0.906 667 | |
| k-means | 0.042 751 | 2.655 840 | 0.886 667 | |
| Wine | Random | 0.559 588 | 1.095 420 | 0.410 112 |
| Hierarchical Clustering | 0.001 574 | 1.666 460 | 0.657 303 | |
| DBSCAN | 1.892 991e-05 | 2.833 750 | 0.943 820 | |
| k-means | 1.818 384e-05 | 2.832 200 | 0.943 820 | |
| Yeast | Random | 0.688 145 | 1.078 260 | 0.357 198 |
| Hierarchical Clustering | 0.003 871 | 0.835 371 | 0.360 277 | |
| DBSCAN | 0.000 711 | 1.304 800 | 0.434 950 | |
| k-means | 7.544 556 e-05 | 1.881 950 | 0.480 370 |
针对iris数据集,利用ECP计算出的p-value与f-score的相关系数为-0.578 018,与accuracy的相关系数为-0.699 331。具体的结果如图 1。针对wine数据集,利用ECP计算得到的p-value与f-score的相系数为-0.535 734,与accuracy的相关系数为-0.538 754。具体的结果为图 2。对于yeast数据集,利用ECP计算得到的p-value与f-score的相关系数为-0.500 340,与accuracy的相关系数为-0.167 325。具体结果为图 3。
从实验结果可以看出用本文方法算出来的p-value是可靠的。需要注意的是yeast的数据集簇结构比较明显,聚类的结果比较集中。
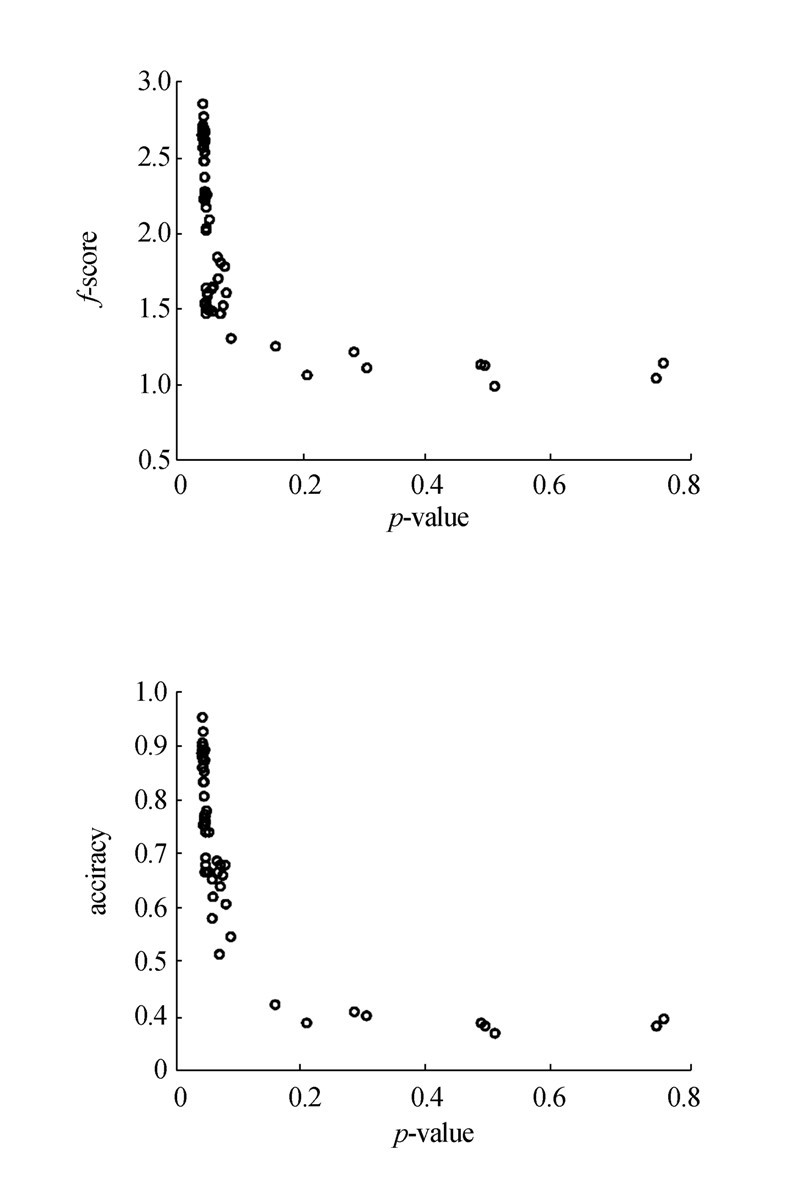 |
| 图 1 Iris数据集p-value与f-score和accuracy的关系Fig. 1 The relationship between p-value and f-score, accuracy of iris dataset |
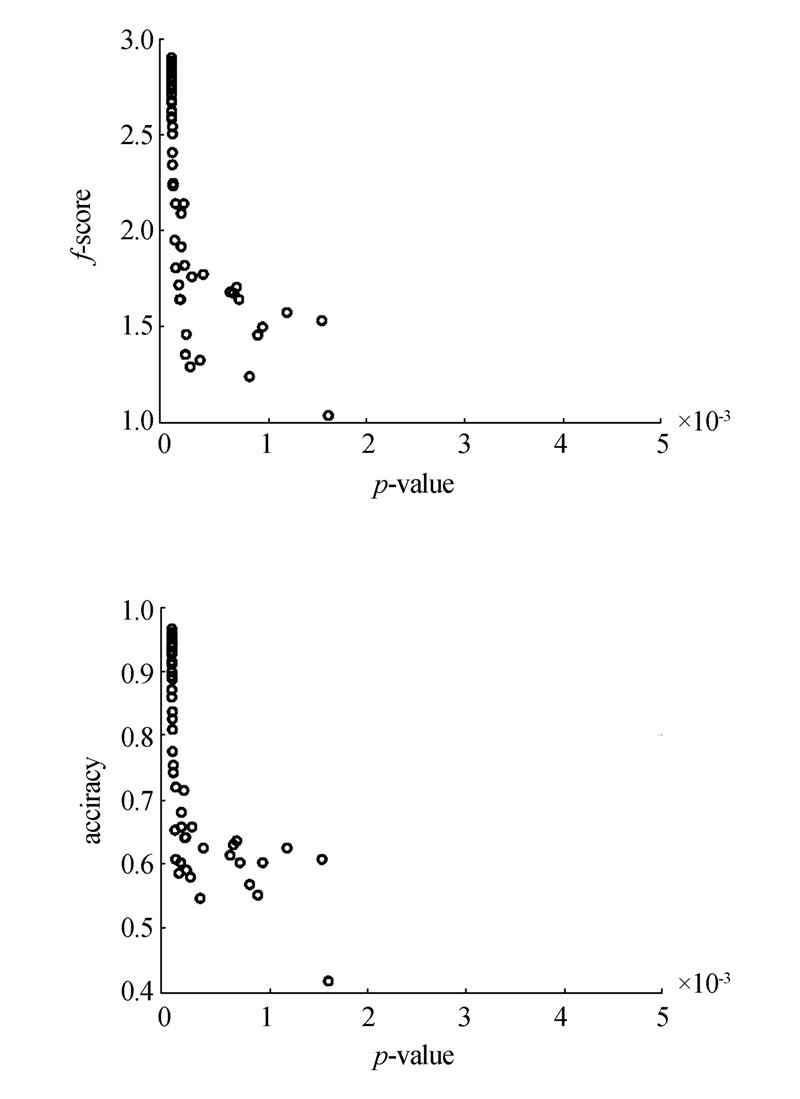 |
| 图 2 Wine数据集p-value与f-score和accuracy的关系Fig. 2 The relationship between p-value and f-score, accuracy of wine dataset |
 |
| 图 3 Yeast数据集p-value与f-score和accuracy的关系Fig. 3 The relationship between p-value and f-score, accuracy of yeast dataset |
很多聚类算法需要预先设定划分数目k。本文研究了p-value与k的关系。对于同一数据集,选择不同的k用k-means分别聚类,然后计算对应的p-value。计算结果如表 2。
从表 2中看出随着k 的增加,p-value 的值变小。因为k越大,对数据集划分得越细,同一个簇内的元素就会越相似,p-value自然就会越小。然而划分的越细并不意味着就一定越好。举个极端的例子,将一个数据量为n的数据集划分成n 个簇是毫无意义的。
本文研究了一种利用p-value 的变化幅度来确定k的新方法。这里给出一个定义:
$R\left( i \right) = \frac{{p\left( {i - 1} \right)}}{{p\left( i \right)}},$
由实验结果可以看出,对于iris数据集,当k取3的时候,R(3) = 2.538 900最大。事实上iris的类别数目就是3。接着看wine数据集,当i取3的时候R(3)= 97.836 510最大。真实情况wine的类别数目就是3。对于yeast数据集当i取4的时候R(4)= 14.991 890最大,以此来确定簇的数目为4。而事实上yeast的类别数目就是4。
利用本文提出的定义能正确算出数据集中的簇数目k。因此可以说明计算聚类的p-value对于确定聚类数目k也是有一定意义的。不过对于R(i)这个定义还存在一定的问题。根据R的定义,i的取值不小于3。因此对于簇数目为2的情况还不能够做出合适的处理。
| 数据 | 2 | 3 | 4 | 5 | 6 | 7 |
| Iris | 0.108 518 | 0.042 742 | 0.020 435 | 0.017 261 | 0.006 991 | 0.003 208 |
| Wine | 0.001 946 | 1.988 773e-05 | 7.579 904e-07 | 2.381 891e-08 | 2.125 773e-09 | 1.537 855e-09 |
| Yeast | 0.006 911 | 0.001 040 | 6.937 873e-05 | 9.647 412e-06 | 1.327 582e-06 | 3.264 579e-06 |
| 数据 | 3 | 4 | 5 | 6 | 7 |
| Iris | 2.538 900 | 2.091 640 | 1.183 870 | 2.469 150 | 2.179 010 |
| Wine | 97.836 510 | 26.237 440 | 31.823 050 | 11.204 820 | 1.382 300 |
| Yeast | 6.644 860 | 14.991 890 | 7.191 430 | 7.266 900 | 0.406 660 |
研究了对于iris、wine和yeast数据集需要多少样本能保证p-value不会因样本数目的增加而改变。对于每个数据集用不同数目样本计算p-value,结果如图 5。
 |
| 图 4 p-value 稳定性Fig. 4 The stability of p-value |
 |
| 图 5 p-value与抽样次数的关系Fig. 5 The relationship between p-value and the number of samples |
实验最多抽取1 000 000个样本。对于这3个数据集,当抽样数目达10 000时p-value就基本稳定了。这一结果证实该方法具有很强的可行性。
4.3 与相关算法对比 4.3.1 ECP与最大熵模型比较本文重复了最大熵模型的评估方法,这3个数据集算出的p-value都为1/N。这是因为样本太少,算法把原始聚类结果也当做一个样本。前文分析了这种做法的不合理性。利用ECP就可以避免这样的情况。除此之外,本文也尝试将最大熵方法的抽样评估值拟合出正态分布。实验结果如表 4。从实验结果可以看出,对于wine数据集,最大熵方法算出的p-value为0.001,拟合正态后的p-value为0.370 035 2。这两者差距比较大,这说明将最大熵方法拟合成正态分布是不合适的。这一实验说明利用ECP评估聚类结果更为可靠。
4.3.2 ECP与SigClust对比SigClust算法是主要针对k为2聚类结果的评估。本文从每个数据集中选出了两类用k-means进行聚类(比如iris数据集中选出了Setosa、Versicolour两类进行对比)。为了让聚类质量有层次的差距,对k-means的聚类结果进行不同程度的破坏。破坏的程度越大,聚类的质量越差。实验结果如表 5。从实验看SigClust与ECP都能够区别出很好和很差的聚类。但是可以很明显地看出,SigClust对聚类质量的区分度不够大。比如对于iris数据集计算的f1为2和1.8,SigClust算出的p-value都是0,没有区分开这2个不同划分的质量。同样地iris数据集f1为1.36和1.158 65,SigClust算出的p-value都为1。实验可以看出ECP能很好地区分聚类质量的差距。因此,与SigClust相比,ECP不仅能处理k>2的情况,而且能更好地评估聚类质量。
| 算法 | iris | wine | yeast |
| 最大熵 | 0.001 | 0.001 | 0.001 |
| 最大熵 拟合正态 | 4.891 817e-05 | 0.370 035 2 | 0.002 626 655 |
| ECP | 0.042 742 13 | 1.988 773e-05 | 6.937 873e-05 |
| 数据 | p-value/ECP | p-value/Sigclust Sigclust | f-score | accuracy |
| Iris | 0.114 572 8 | 0 | 2 | 1 |
| 0.121 688 1 | 0 | 1.8 | 0.9 | |
| 0.157 168 9 | 1 | 1.36 | 0.68 | |
| 0.228 296 5 | 1 | 1.158 65 | 0.58 | |
| wine | 0.001 534 783 | 0 | 1.876 81 | 0.938 462 |
| 0.002 878 496 | 0.199 2 | 1.673 66 | 0.838 462 | |
| 0.006 082 356 | 1 | 1.430 74 | 0.715 385 | |
| 0.221 656 | 1 | 1.011 64 | 0.546 154 | |
| yeast | 0.006 761 993 | 0 | 1.130 05 | 0.567 265 |
| 0.010 775 1 | 1 | 1.077 86 | 0.539 238 | |
| 0.012 549 87 | 1 | 1.073 48 | 0.536 996 | |
| 0.256 406 2 | 1 | 1.044 03 | 0.522 422 |
这一部分说明ECP比加速的ECP1在效率上有很大提高。ECP1是未加速的ECP算法。本文将这两种算法进行了效率上的对比。实验结果如表 6。实验分别用两种算法抽样100 000次并得到对应的统计值。可以看出,对于iris数据集,ECP比ECP1快了60倍。可见ECP在效率上有质的提升。
| 算法 | iris | wine | yeast |
| ECP1 | 18 s | 50 s | 56s |
| ECP | 1109 s | 734 s | 280 m |
本文提出了一种新的基于置换检验的聚类结果评估方法ECP。为了增大抽样的数目,利用DB-Index的计算特点减小了对样本函数值计算的复杂度。为了得到更精确的p-value,根据聚类划分的特点,假设了DB-Index的函数值是符合高斯分布的,进而可以用较少的抽样估出更为准确的p-value。从实验的结果来看,ECP对评估聚类结果有很好的效果,并且具有很强的实用性。
| [1] | TAN Pangning, STEINBACH M, KUMAR V. Introduction to data mining[M]. Boston: Addison-Wesley, 2005. |
| [2] | HAN Jiawei, KAMBER M, PEI Jian. Data mining: concepts and techniques[M]. 3rd ed. Burlington, MA, USA: Elsevier, 2012: 1-33. |
| [3] | 尹宏伟, 李凡长. 谱机器学习研究综述[J]. 计算机科学与探索, 2015, 9(12): 1409-1419. YIN Hongwei, LI Fanzhang. Survey on spectral machine learning[J]. Journal of frontiers of computer science and technology, 2015, 9(12): 1409-1419. |
| [4] | JAIN A K, MURTY M N, FLYNN P J. Data clustering: a review[J]. ACM computing surveys, 1999, 31(3): 264-323. |
| [5] | WU Xindong, KUMAR V, QUINLAN J R, et al. Top 10 algorithms in data mining[J]. Knowledge and information systems, 2008, 14(1): 1-37. |
| [6] | HALKIDI M, BATISTAKIS Y, VAZIRGIANNIS M. On clustering validation techniques[J]. Journal of intelligent information systems, 2001, 17(2-3): 107-145. |
| [7] | HANDL J, KNOWLES J, KELL D B. Computational cluster validation in post-genomic data analysis[J]. Bioinformatics, 2005, 21(15): 3201-3212. |
| [8] | KONTONASIOS K N, VREEKEN J, DE BIE T. Maximum entropy modelling for assessing results on real-valued data[C]//Proceedings of the 11th international conference on data mining. Vancouver, BC, Canada, 2011: 350-359. |
| [9] | OJALA M. Assessing data mining results on matrices with randomization[C]//Proceedings of international conference on data mining. Sydney, Australia, 2010: 959-964. |
| [10] | OJALA M, VUOKKO N, KALLIO A, et al. Randomization methods for assessing data analysis results on real-valued matrices[J]. Statistical analysis and data mining, 2009, 2(4): 209-230. |
| [11] | LIU Yufeng, HAYES D N, NOBEL A, et al. Statistical significance of clustering for high-dimension, low-sample size data[J]. Journal of the American statistical association, 2008, 103(483): 1281-1293. |
| [12] | PARK P J, MANJOURIDES J, BOONETTI M, et al. A permutation test for determining significance of clusters with applications to spatial and gene expression data[J]. Computational statistics & data analysis, 2009, 53(12): 4290-4300. |
| [13] | 张刚, 刘悦, 郭嘉丰, 等. 一种层次化的检索结果聚类方法[J]. 计算机研究与发展, 2008, 45(3): 542-547.ZHANG Gang, LIU Yue, GUO Jiafeng, et al. A Hierarchical search result clustering method[J]. Journal of computer research and development, 2008, 45(3): 542-547. |
| [14] | KNIJNENBURG T A, WESSELS L F A, REINDERS M J T, et al. Fewer permutations, more accurate p-values[J]. Bioinformatics, 2009, 25(12): i161-i168. |
| [15] | ASUNCION A, NEWMAN D J. UCI machine learning repository[EB/OL]. 2007. http://archive.ics.uci.edu/ml/. |



