SAR固有的相干成像方式会导致描述同一目标场景的多幅图像之间出现几何和辐射差异。图像匹配通过将两幅图像的相似性进行比较,根据比较结果快速地进行SAR图像识别,成为进一步挖掘目标场景信息变化的前提[1]。
图像之间的相似性度量可以通过构建SAR图像特征描述子进行衡量,国内外学者对特征描述子的相关算法进行了大量研究。在光学图像领域中,局部二值模式(local binary pattern,LBP)[2]是一种描述中心像素点与周围像素点灰度大小关系的纹理算法,该方法计算简单且具有部分尺度、旋转和亮暗不变性等优点,被广泛地应用于人脸图像分析、目标检测与跟踪等领域[2-5]。为提高纹理特征的准确性,Mäenpää等[6]通过限制二值化编码中0/1或1/0跳变的次数,将基本LBP模式分为统一模式和非统一模式,大大提高了图像信息获取的指向性。Ojala等[7]对统一模式进一步划分,将不同方向上表示相同结构的统一模式合并归类,提出了旋转不变统一LBP方法,使提取到的图像信息具备抗旋转性能。在SAR图像领域中,局部模式直方图(local pattern histogram,LPH)[8]是一种针对SAR图像的纹理算子,该方法通过图像量化编码和直方图计算,得到图像纹理特征信息,实现了高精度的SAR图像分类。局部梯度比率直方图(local gradient ratio pattern histogram,LGRPH)[9]是一种比率测度算子,克服了SAR图像的相干斑噪声和局部梯度变化,有效地用于SAR图像目标识别。
总体而言,目前的局部算子研究都只能用于图像纹理信息提取。由于LBP算子是基于像素灰度的差值计算,在SAR图像中受乘性噪声的严重影响,精确性差,因此在SAR图像中不适用。而基于局部模式的LPH算子忽略了邻域像素的相关性,从而影响SAR图像特征提取的准确性[10]。同时基于梯度比率的LGRPH算子缺少对方向角度的描述,因此在SAR图像中对目标的旋转变化不鲁棒。针对上述问题,本文分析了LBP与旋转不变LBP的数学模型和算法原理,引入了适合SAR图像噪声环境的LGRP算子,并对其进行旋转不变改进与实验验证。基于LGRPH特征的旋转不变特性,设计了SAR图像目标分类识别实验和纹理对比实验,实验结果表明本文所改进的LGRP特征能克服SAR图像乘性噪声的影响,对目标的旋转变化有很好的鲁棒性。
1 局部二值模式 1.1 局部二值模式的数学基础局部二值模式通过对局部二值化的邻域像素进行编码,能够有效地提取图像纹理信息,其计算流程如图 1所示。在3×3邻域内,分别比较周围像素值gp与中心像素值gc的大小,由判别函数s(x)得到二值化编码串的值,即为LBP特征值。计算公式如下:

|
图 1 LBP算子计算过程 Fig.1 Calculation process of the original LBP |
| $ {\rm{LB}}{{\rm{P}}_{P, R}} = \sum\limits_{P = 0}^{P-1} {s\left( {{g_{\rm{p}}}-{g_{\rm{c}}}} \right){2^P}} $ |
式中:P为邻域像素个数;R为邻域半径;判别函数的表达式为
图像的旋转变化会导致基本LBP算子的二进制编码循环移位,从而计算的特征值发生变化,因此引入旋转不变局部二值模式(以下简称旋转不变LBP),记为LBPri。LBPri首先采用圆形邻域,等间隔采样点后再分别与中心像素进行二值化计算,将具有相同最小或最大编码的模式合并为一种新的模式。具体计算公式为
| $ {\rm{LBP}}_{P, R}^{ri} = \min \left\{ {{\rm{ROR}}\left( {{\rm{LB}}{{\rm{P}}_{P, R}}, i} \right)\left| {i = 0, 1, \cdots, P-1} \right.} \right\} $ |
式中ROR(x, k)表示对P位二进制数向右循环移位k次(|k|≤P)。
通过定义旋转不变,使得LBP算子对图像旋转更加鲁棒,进一步减少了LBP算子的模式种类。
1.3 光学与SAR图像中LBP算子的抗旋转性比较分析基本LBP和旋转不变LBP均为描述纹理特征的局部算子,相比前者,后者利用循环位移使算子具有了旋转不变性。下面通过光学图像和SAR图像的实验对比,分析旋转不变LBP算子对图像旋转的鲁棒性和LBP算子对SAR图像的不适用性,如图 2和图 3所示。
|
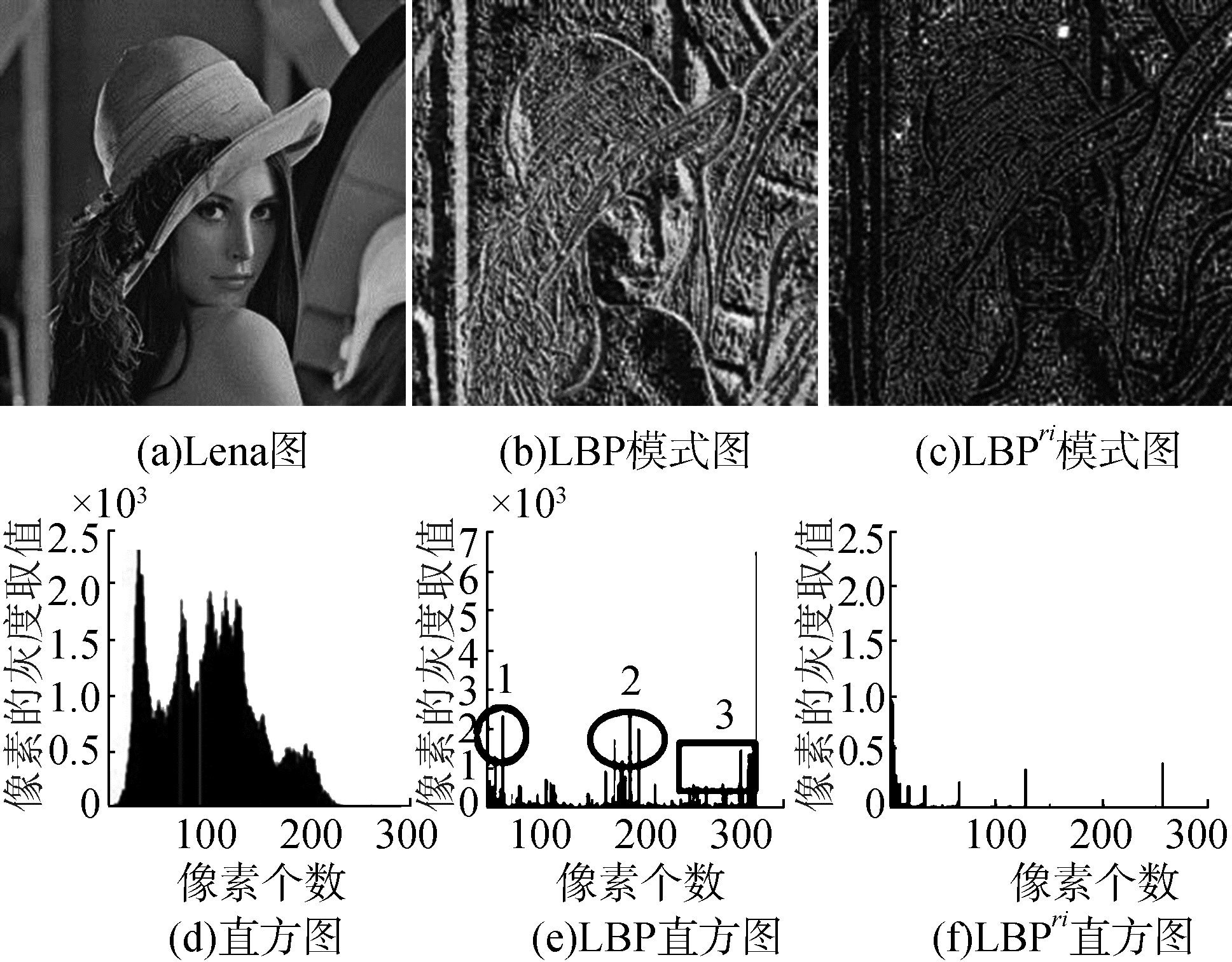
图 2 图像旋转前LBP和旋转不变LBP算子比较 Fig.2 Comparison of LBP and rotation invariant LBP operator before image rotation |

|
图 3 图像旋转后LBP和旋转不变LBP算子比较 Fig.3 Comparison of LBP and rotation invariant LBP operator after image rotation |
从图 2(c)和图 3(c)可以看出,旋转前后LBP算子计算的直方图有明显变化,说明基本LBP算子对图像旋转变化不具有鲁棒性。从图 2(f)和图 3(f)可以看出,旋转不变LBP算子在图像旋转前后计算的直方图基本保持不变,说明旋转不变LBP算子对光学图像旋转具备抗旋转性。
1.3.2 SAR图像实验选用MSTAR数据库中T72、BMP2和BTR70等3种不同类型目标的图片数据,仿真分析LBP算子和旋转不变LBP算子在SAR图像中的适用性。实验分为两个部分:1) 对不同姿态角的T72目标SAR图像进行特征提取,分析LBP和旋转不变LBP的性能;2) 对多种目标进行特征提取,分析LBP和旋转不变LBP算子的识别性能。
仿真结果表明,图 4(e)和图 5(e)、图 4(f)和图 5(f)中图像旋转前后计算得到的直方图无明显变化,出现这种结果有以下两种解释:1) 基本LBP和旋转不变LBP算子在SAR图像中对目标姿态角度变化不敏感;2) LBP算子在SAR图像中失效,提取的特征不稳健。

|
图 4 T72旋转前LBP和旋转不变LBP对比实验 Fig.4 Comparison of LBP and rotation invariant LBP operator before T72 image rotation |

|
图 5 T72旋转后LBP和旋转不变LBP对比实验 Fig.5 Comparison of LBP and rotation invariant LBP operator after T72 image rotation |
为了分析上述两种解释的真实性,下面分别用BMP2和BTR70数据图像对基本LBP和旋转不变LBP进行实验,仿真结果如图 6和图 7所示。

|
图 6 BTR70系列图像实验 Fig.6 Experiments on BTR70 series image |

|
图 7 BMP2系列图像实验 Fig.7 Experiments on BMP2 series image |
实验对比表明,对于SAR图像目标,在相同角度和不同角度的情况下,以及相同目标和不同目标图像,基本LBP和旋转不变LBP计算的直方图都基本相似,说明基本LBP和旋转不变LBP算子对SAR图像不适用。
分析原因如下:对SAR图像而言,由于图像存在大量相干斑噪声,根据像素差值计算的二值编码串易受乘性噪声影响,因此LBP算法不能有效克服相干斑噪声,不能有效地描述SAR图像目标特性。
针对LBP算子的不适用性,本文提出的解决方案是将比率测度引入局部二值模式,从而有效地克服SAR图像的乘性噪声,最终运用于SAR图像的特征提取。
2 改进的LGRP特征提取方法 2.1 局部梯度比率二值模式LBP算法易受乘性相干斑噪声的影响,对图像局部梯度变化不敏感,例如在边缘、角点处LBP特征描述并不有效。针对SAR图像相干斑噪声和图像局部梯度特性,项德良等[9]提出了基于局部梯度比率特征的二值模式。
对于局部梯度比率特征的构建,首先计算每个邻域像素gp与中心像素gi, j的灰度差值的绝对值作为该邻域像素的梯度值计算过程如式(3):
| $ {G_{{\rm{difference}}}}\left( {{g_p}} \right) = \left| {{g_p}-{g_{i, j}}} \right| $ | (3) |
将该邻域像素的梯度值与其自身灰度值的比值作为该邻域像素的梯度比率特征值(gradient ratio pattern,GRP),即
| $ {G_{{\rm{ratio}}}}\left( {{g_p}} \right) = \frac{{{G_{{\rm{difference}}}}\left( {{g_p}} \right)}}{{{g_p}}} $ | (4) |
然后,将所有邻域像素的GRP均值分配给中心像素作为其GRP,其中P为邻域像素个数,具体如式(5):
| $ \overline {{G_{{\rm{ratio}}}}\left( g \right)} = \frac{1}{P}\sum\limits_{p = 1}^P {{G_{{\rm{ratio}}}}\left( {{g_p}} \right)} $ | (5) |
最后,计算每个邻域像素与中心像素的GRP之差,再由判别函数s(x)生成二值化编码串,计算其值作为中心像素的LGRP特征值,其中R为邻域半径,如式(6) 所示:
| $ {\rm{LGR}}{{\rm{P}}_{P, R}}\left( {{g_{i, j}}} \right) = \sum\limits_{P = 0}^{P-1} s \left( {{G_{{\rm{ratio}}}}\left( {{g_p}} \right)-\overline {{G_{{\rm{ratio}}}}\left( g \right)} } \right){2^P} $ | (6) |
统计所有像素的LGRP值形成的灰度直方图就是LGRPH。以一幅N×M大小的图像为例,计算整幅图像的LGRPH:
| $ {\rm{LGRPH}}\left( k \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {f\left( {{\rm{LGR}}{{\rm{P}}_{P, R}}\left( {{g_{i, j}}} \right), k} \right)}, k \in \left[{0, K} \right]} $ |
其中K为LGRP最大的编码值,函数f的表达式为
| $ f\left( {x, y} \right) = \left\{ \begin{array}{l} 1, \;\;\;\;x = y\\ 0, \;\;\;\;其他 \end{array} \right. $ |
具体计算过程如图 8所示。

|
图 8 LGRP特征计算过程 Fig.8 Calculation process of the LGRP feature |
基于梯度比率的LGRP算子对乘性相干斑不敏感,对梯度变化也有一定鲁棒性,但对SAR图像中目标姿态角变化没有鲁棒性。针对LGRP特征对SAR图像中目标姿态角变化不敏感的问题,本文提出一种改进的旋转不变LGRP特征提取方法。首先根据LGRP特征的计算思路求得所有像素的二进制编码,再通过循环位移对二进制模式进行合并,构建旋转不变LGRP特征。具体步骤如下:
1) 根据前文介绍的LGRP算子计算公式,计算得到所有邻域像素的GRP值,再由判别函数s(x)生成二进制编码串。
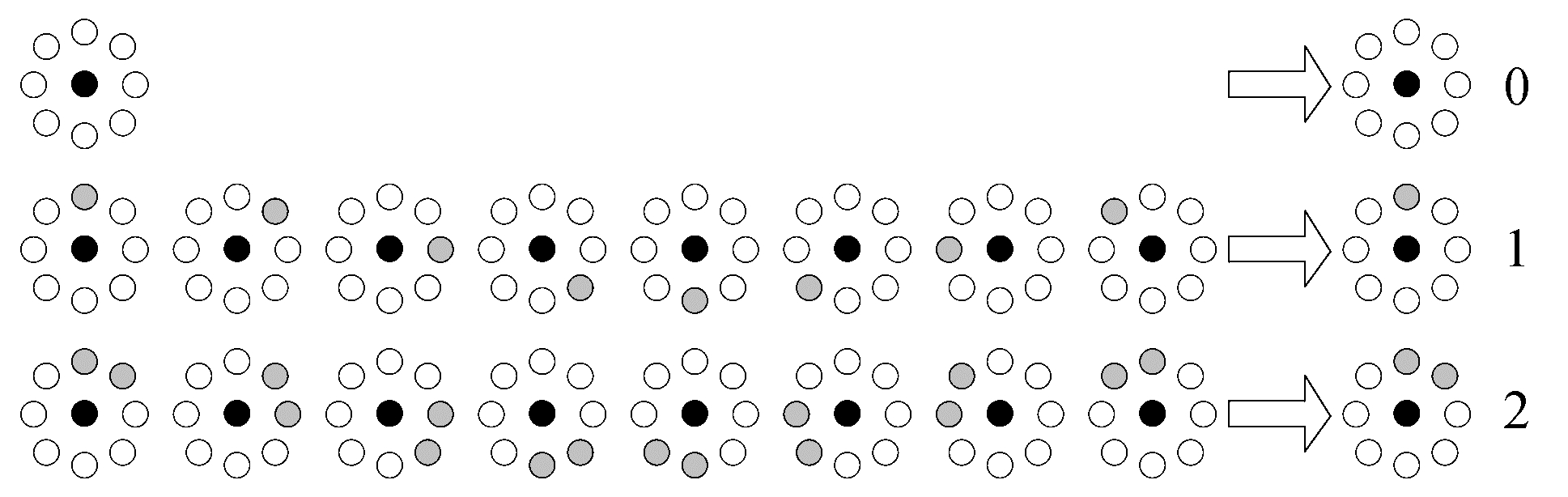
2) 对循环移位后可得到相同最小二进制模式的编码模式进行合并。以4位的二进制编码为例,编码1110(14)、1101(13)、1011(11) 和0111(7) 通过循环移位均可达到最小的编码0111。根据旋转不变LBP思路,这4种模式将会合并为一种新的模式。以8邻域采样点为例,合并过程如图 9所示。
|
图 9 合并模式的映射关系 Fig.9 The mapping relation of merging pattern |
3) 对于合并后得到的新模式,分别计算其值作为相应像素的特征值。
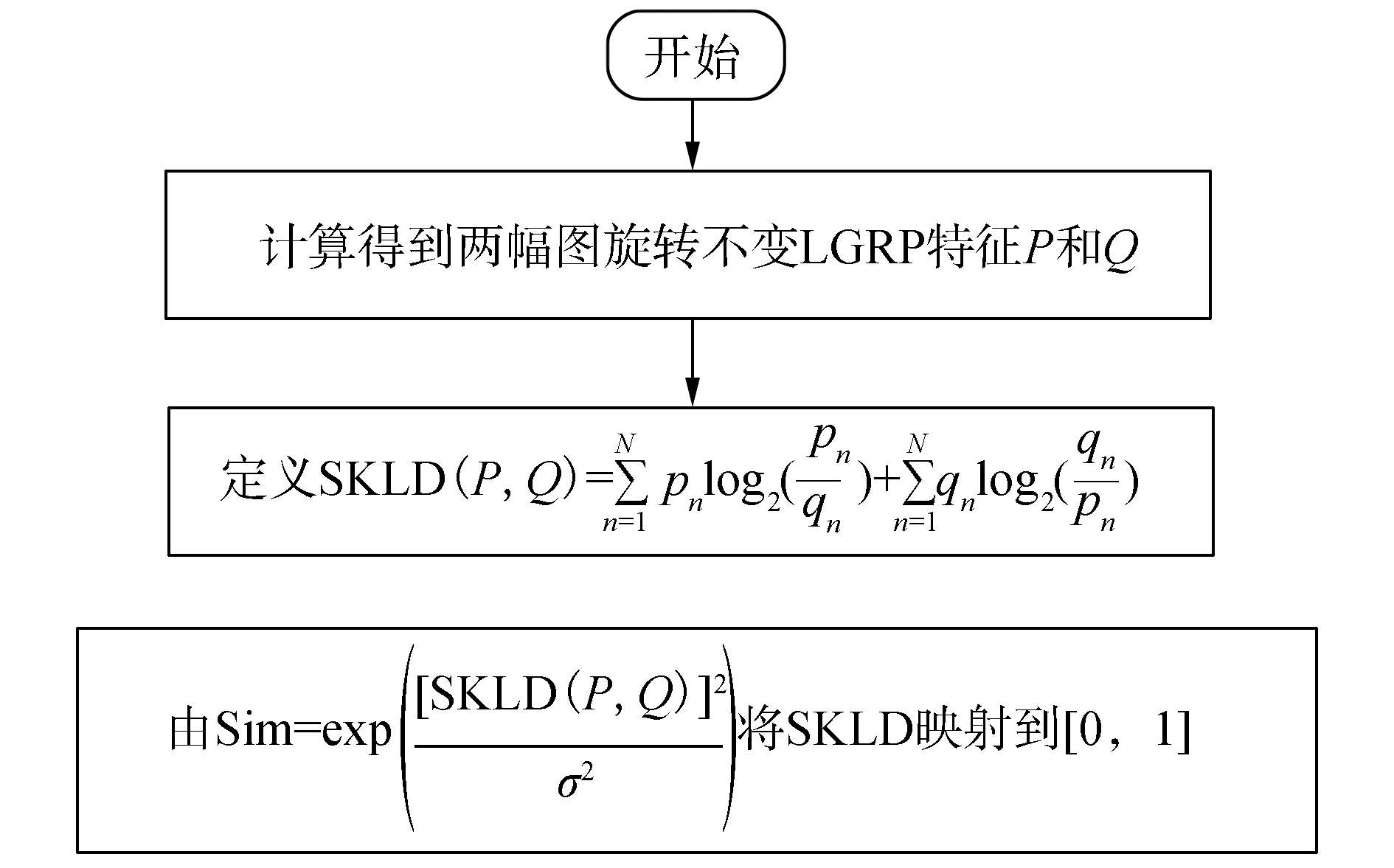
4) 计算得到旋转不变LGRP特征后,采用对称KL准则SKLD(symmetry kullback-leibler divergence)[11]来比较不同图像的特征。其流程图如图 10所示。
|
图 10 相似度计算流程 Fig.10 Calculation process of the similarity |
本文实验数据包括美国国防高级研究计划署和空军研究室对外发布的MSTAR(moving and stationary target acquisition and recognition) SAR数据集和X波段Terra-SAR的香港地区遥感图像。
实验选用MSTAR中BMP的图像数据,并将邻域半径最小值Rmin设为1,收敛步长d设为1,控制高斯函数宽度的参数σ设为2,分析邻域采样点数P和最大邻域半径Rmax对旋转不变LGRP特征构造的影响。
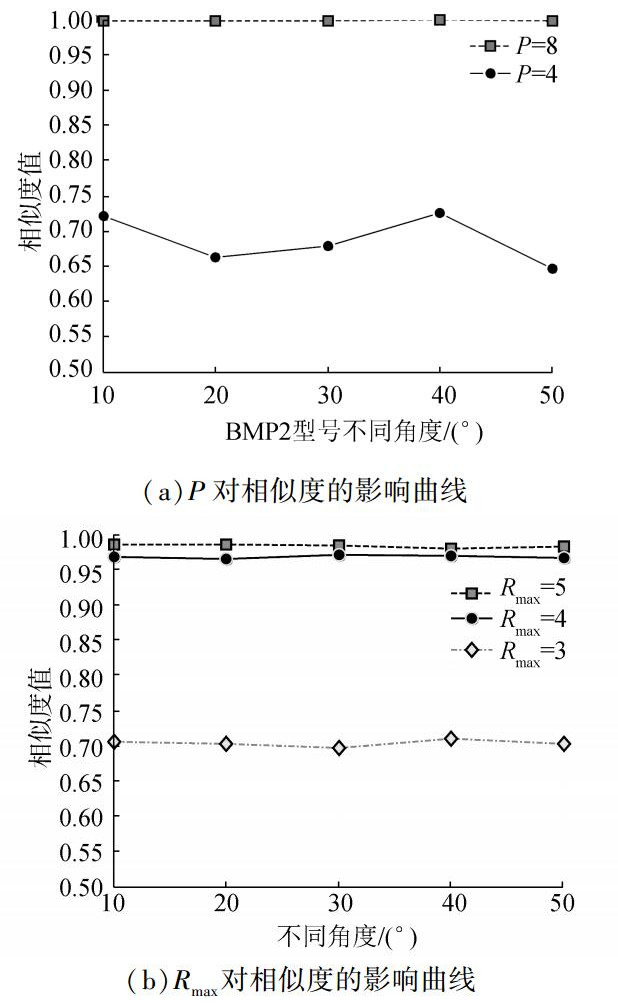
如图 11(a)示,当固定Rmax取值时,P=4或P=8计算得到的LGRP相似度对噪声都有一定的鲁棒性,但P=8时相似度曲线波动性更小,这是由于邻域选择8个点比选择4个点利用的局部信息更丰富,从而对噪声鲁棒性更强。在图 11(b)中,当固定P取值时,不同Rmax取值曲线的走向一致,且取值越大稳定性越好,同时计算也越耗时。表 1和表 2分别给出了曲线的具体取值。
|
图 11 参数P和Rmax对相似度曲线的影响 Fig.11 The influence of parameter P and Rmax on similarity curve |
| 表 1 采样点数P对相似度的影响曲线具体取值 Tab.1 Specific value of similarity curve under the influence of P |
| 表 2 Rmax对相似度的影响曲线具体取值 Tab.2 Specific value of similarity curve under theinfluence of Rmax |
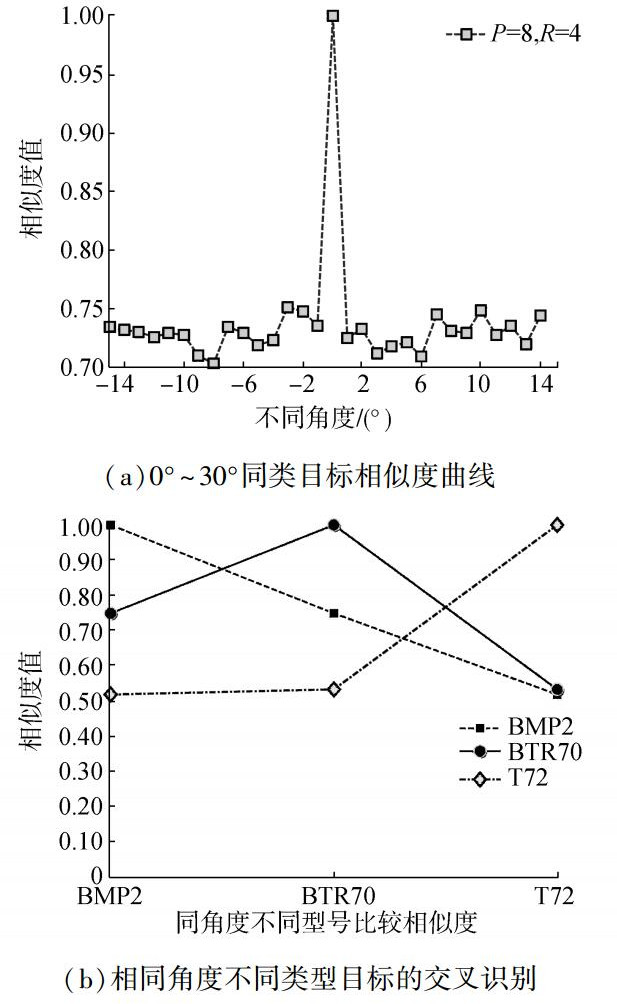
实验分为两个部分:1) 同类目标不同姿态角的相似度比较,仿真选用0°~30°范围BMP的图片数据,验证LGRP相似度的稳定性;2) 相同姿态角不同目标的交叉识别,仿真选用相同角度的BMP2_0和BTR70_0以及T72_0等3种不同型号的目标图片,验证LGRP特征可用于目标识别。实验仿真结果如图 12所示。
|
图 12 同类目标比较和不同目标识别的相似度曲线 Fig.12 The similarity curves of similar objective comparison and different target recognition |
从图 12(a)中曲线可以看出,对于不同姿态角的BMP2目标,旋转不变LGRP计算的特征相似度取值稳定,说明旋转不变LGRP对目标姿态角变化具有鲁棒性。从图 12(b)可以看出,LGRP对于不同目标具有分辨能力,可用于SAR图像目标识别中。
3.3 SAR图像纹理识别实验实验数据选用不同旋转角度的香港地区Terra-SAR图像中同类型地物的纹理切片(见图 13),选择4个不同角度下的同类地物纹理切片进行仿真实验。实验中对图像切片分别提取LBP特征、LGRP特征和LPH特征,并且分析其与原始角度下的图像切片特征的相似度大小,考察上述3种纹理特征算子对不同旋转角度纹理切片的识别能力。

|
图 13 四种不同角度的城区纹理切片 Fig.13 The texture slices of urban in different |
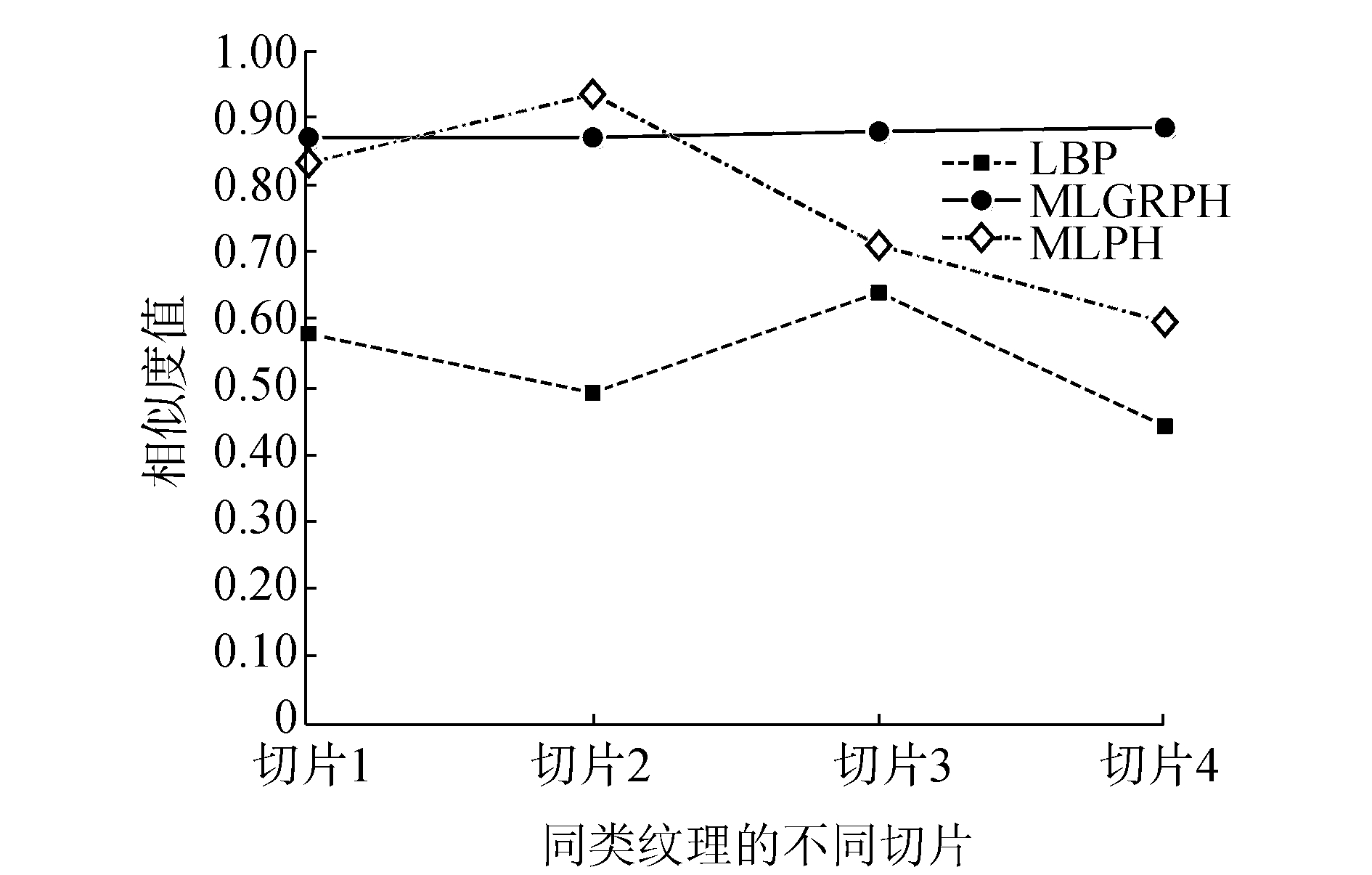
由图 14的仿真结果可以看出,LBP算子计算的特征稳定性最低,不适用于SAR图像的纹理特征提取与识别,原因在2.3节已经分析过。LPH算子的稳定性劣于旋转不变LGRP算子,原因如下:1) LPH算子是对中心像素的灰度值与邻域像素进行比较二值化,在SAR图像中单个像素灰度值易受相干斑噪声干扰,稳定性差;2) LPH算子在合并子直方图时省略了部分信息,有可能导致某些重要特征丢失,使最后计算的特征不够稳定;3) LPH算子是在选定的邻域范围内构建直方图,忽视了邻域像素之间的相关性[10]。通过实验结果分析,本文提出的改进后的LGRP算子对旋转变化下的纹理切片识别具有较好的鲁棒性。
|
图 14 不同算子间性能比较相似度曲线 Fig.14 Performance comparison curve betweendifferent operators |
本文研究了用于描述SAR图像特征的局部二值模式,通过实测SAR图像的不同角度对比实验以及旋转变化下的纹理识别实验,验证了本文改进的LGRP算子对SAR图像目标的姿态角变化有一定的鲁棒性,能有效用于SAR图像目标分类、识别等应用。将具有抗旋转性的LGRP算子运用到SIFT算子的特征描述中,结合SIFT算子的优势寻找一种适合SAR图像特征提取的新方法将是下一步工作的重点。
| [1] |
SONG C, YANG F, LI P. Rotation invariant texture measured by local binary pattern for remote sensing image classification[C].Education Technology and Computer Science (ETCS), 2010 Second International Workshop on. IEEE, 2010, 3: 3-6. https://www.researchgate.net/publication/232641723_Rotation_Invariant_Texture_Measured_by_Local_Binary_Pattern_for_Remote_Sensing_Image_Classification
( 0) 0)
|
| [2] |
OJALA T M, HARWOOD D. A comparative study of texture measures with classification based on featured distributions[J]. Pattern recognition, 1996, 29(1): 51-59. DOI:10.1016/0031-3203(95)00067-4 ( 0) 0)
|
| [3] |
AHONEN T, HADID A M. Face description with local binary patterns: Application to face recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2006, 28(12): 2037-2041. DOI:10.1109/TPAMI.2006.244 ( 0) 0)
|
| [4] |
AHONEN T, HADID A, M. Face recognition with local binary patterns[J]. European conference on computer vision, 2004, 3021(12): 469-481. ( 0) 0)
|
| [5] |
NING J, ZHANG L, ZHANG D, et al. Robust object tracking using joint color-texture histogram[J]. International journal of pattern recognition and artificial intelligence, 2009, 23(07): 1245-1263. DOI:10.1142/S0218001409007624 ( 0) 0)
|
| [6] |
Topi M, Timo O, Matti P, et al. Robust texture classification by subsets of local binary patterns[C]//Proceedings of the 15th International Conference on Pattern Recognition. 2000. IEEE, 2000, 3(3): 935-938. https://www.researchgate.net/publication/220931208_Robust_Texture_Classification_by_Subsets_of_Local_Binary_Patterns
( 0) 0)
|
| [7] |
Ojala T, Pietikäinen M, Mäenpää T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE transactions on pattern analysis and machine intelligence, 2002, 24(7): 971-987. DOI:10.1109/TPAMI.2002.1017623 ( 0) 0)
|
| [8] |
DAI D, YANG W, SUN H. Multilevel local pattern histogram for SAR image classification[J]. IEEE geoscience and remote sensing letters, 2011, 8(2): 225-229. DOI:10.1109/LGRS.2010.2058997 ( 0) 0)
|
| [9] |
项德良, 粟毅, 赵凌君, 等. 一种基于局部梯度比率特征度量SAR图像相似性的新方法[J]. 电子学报, 2014, 01: 9-13. XIANG Deliang, SU Yi, ZHAO Lingjun, et al. A new algorithm for SAR imagery similarity measure based on local gradient ratio pattern[J]. Acta electronica sinica, 2014, 01: 9-13. DOI:10.3969/j.issn.0372-2112.2014.01.002 (  0) 0)
|
| [10] |
GUAN Dongdong, TANG Tao, ZHAO Ling-jun, et al. A feature combining spatial and structural information for SAR image classification[C].Geoscience and Remote Sensing Symposium (IGARSS), 2015 IEEE International. IEEE, 2015: 4396-4399. http://ieeexplore.ieee.org/document/7326801/
( 0) 0)
|
| [11] |
LI L, TONG C S, CHOY S K. Texture classification using refined histogram[J]. IEEE transactions on image processing, 2010, 19(5). ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


