2. Department of Mathematics, Dalian Maritime University, Dalian 116026, China
在经济全球化日渐凸显,航运联盟正发挥其巨大优势的今天,区域港口群内部港口之间必须要建立必要的竞争合作战略关系,依靠整体力量共同面对国际竞争。因此,港口之间的关系也正在逐渐由单纯的竞争或合作转变为“竞合”、“双赢”的多元化关系模式,港口之间为竞争而合作,以合作求竞争是未来港口关系发展的新趋势[1]。区域港口群中,港口间的多元化竞合关系更加紧密,形成了区域港口群内部的竞合网络。在该网络中,港口间的这种多元化竞合关系体现出了复杂网络的一种普遍属性“关系的多重性”[2]。所谓“关系的多重性”,即网络中相同的一组行动者节点,可从不同角度出发,拥有多种不同的关系类型。
一方面,是区域港口群内部港口竞合关系的多元化;另一方面,集装箱船超大型化趋势促使共享腹地的区域港口群逐渐形成了层次化、网络化的竞合格局。在这样的大环境下,如何规划港口布局,形成层次分明、定位明确、合理分工的良性港口群竞合关系网络,已成为港口管理决策人员非常关注的问题,也是区域港口群提升整体竞争力所亟待解决的问题。
以往的网络分析模型中,只关注单一性质的关系[3],若要研究多重关系,需要构建多个网络模型,且需针对每种不同性质的关系单独制作数据文件,单独分析,单独输出,无法实现多重关系同时分析,以及分析的输入、输出自动化和程序化。为解决以上问题,本文引入了基于多维基元的复杂社会网络[4]构建方法构建区域港口群竞合网络,利用基元理论的优势,定义了“港口群网络物元”、“港口节点物元”及“港口竞合关系元”,基于此构建了区域港口群竞合网络。
本文基于社会网络分析 (social network analysis, SNA) 方法,针对如何在区域港口群竞合网络中正确定位港口功能,如何规划和建立最优港口群竞合关系,进行了分析研究和探索。最终选取珠三角港口群主要港口进行了实例分析,并使用MATLAB实现了分析的全部过程。
1 基于基元网络模型的区域港口群竞合网络构建基元理论由我国学者蔡文教授提出,它把物、事、关系,特征和量值分别统一在一个三元组中,从而形式化描述物、事和关系[5]。社会网络的基元网表示方法阐述了社会个体成员形成物元网的表示方法[6]。本节基于多维基元的复杂社会网络模型[4],建立了区域港口群内多个港口之间的竞合关系网络。
在本文中的区域港口群竞合关系网络中,网络中的节点由港口对象拓展为港口物元节点,物元节点完整地反映了节点自身所拥有的特征属性;网络中的连线由港口之间的单一关系拓展为港口竞合关系元,港口竞合关系元不但包含港口之间多元、复杂的竞合关系影响因素,描述了多种类型的竞争关系及合作关系,本文主要关注横向竞合关系 (主要指货源竞争) 和纵向竞合关系 (主要指喂给关系)。
1.1 港口节点物元定义1 以网络中的节点Om为对象,n个特征cm1,cm2,…,cmn以及Om关于cmi(i=1, 2, …, n) 对应的特征值vmi(i=1, 2, …, n) 所构成的阵列称为n维节点物元,用M表示,作为复杂社会网络的基本组成。
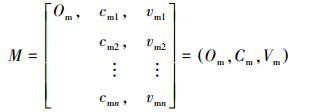 |
由定义1,首先建立区域港口群的物元网络。设区域港口群有n个港口对象,分别为Pi(i=1, 2, …, n),因此第i个港口节点物元为Mi可表示为
 |
港口节点物元中可包含港口节点的基本信息、网络分析所需的港口特征、特征值及网络结构分析的结果。
1.2 港口竞合关系元网络分析的研究重点是节点之间的“关系”。以往研究中,节点间关系数据只停留在“有 (1)”“无 (0)”或某个程度 (数值)。将“关系”拓展为“关系元”,可表示关系的多种特征及其特征值,充分体现出了复杂社会网络中关系的“多重性”,是描述网络中关系的最优形式化范式。
本文研究的区域港口群网络纵向竞合主要是指以枢纽港为中心,上下游支线港、喂给港组成的港口喂给系统内外的竞争与合作;横向竞合主要包括港口对腹地货源的竞争[7]。
根据关系元[8]的定义及表示方法的规范[6],港口竞合网络中的关系元可表示为
 |
式中,i=1, 2, …, n; j=1, 2, …, n; k=1, 2, …, m。港口竞合关系元用于描述港口Pi与港口Pj之间的竞合关系,为方便起见,可将上述关系元记作Rij(竞合关系,Pi, Pj)。关系元可存储港口的各类竞合关系的特征及其特征值。
最后还需要建立一个包含n个港口的区域港群网络物元,其主要作用是表示和存储网络整体属性,如网络密度、网络中心势等。
设Gm可表示为
 |
区域港口群内港口之间的竞争合作网络由节点物元集合、竞合关系元集合及港口群网络物元构成。
2 区域港口群竞合网络分析过程 2.1 网络层次结构分析——层次聚类港口网络层次结构是指在港口布局网络中,根据自然条件、腹地经济、地理通达性等硬件条件和港口服务效率、服务质量等软件条件,将港口划分为全球枢纽港、区域枢纽港、支线港或喂给港等层次结构。港口网络的各个层次之间是互相联系,协调发展的[9]。
本文利用社会网络分析方法中的网络层次聚类法来划分港口群中的港口层次格局,利用一般分类效果最好的“Ward法”[10](离差平方和法) 结合“欧氏距离”进行聚类分析。
2.1.1 聚类指标港口规模的评价指标主要包括港口基础设施、自然情况、腹地经济水平、吞吐量等,本文选取“最大吃水泊位水深”“城市人均GDP” “生产性码头泊位数” “货物吞吐量” “集装箱吞吐量”5个港口规模聚类指标,从港口节点物元中提取相应的特征及特征值。
2.1.2 参数设置n为区域港口群港口数量;K为目标聚类个数;p为聚类指标维度;Gt为在t阶段的一个聚类;Xi(t)为Gi中的第i个港口样本,是一个p维向量;nt为Gt中的样本个数;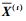
1) 初始每个港口样本自成一聚类,可表示为G1, G2, …, Gn。
2) 计算各聚类内部的“离差平方和”,即
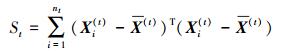 |
(1) |
3) 计算每种聚类合并方案所产生的“离差平方和”增量,假设将聚类Gp和Gq合并为Gm,增量计算公式为
 |
(2) |
选取离差平方和增量最小的合并方案进行实际的合并操作。
4) 重复2) 和3) 直到所有样品合并为一类。
5) 根据可接受的节点,得出港口的K个港口网络层次,记为Lev1,Lev2,…,LevK。
2.2 网络特性分析——社会网络分析 2.2.1 网络密度分析港口竞合网络的密度分析,是指网络中实际存在的关系占所有可能存在的关系的比例,表明了港口竞争合作关系的“密集程度”,因此过大或过小的竞合网络密度都代表港口群内部竞合结构并非最优化[11],计算公式如下:
 |
港口群竞合网络中,每个港口扮演着不同的角色,对网络中其他成员的“影响力”也有着巨大的差异。中心性反映了网络中港口在等级和优势等方面的差异,是网络结构的重要属性。对中心性的研究可以加深对“权利”的量化认识[12]。
1) 度数中心度。
度数中心度 (degree centrality),体现了某港口在竞合网络结构中的“核心”程度[13],记为CD(Pi)。从港口的中心度分析中可以得出各港口对竞合关系网结构的影响程度,分辨出扮演“结构中心”角色的港口。有向图的度数中心度分为入度中心度和出度中心度。计算公式如下:
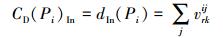 |
(3) |
 |
(4) |
2) 中心势。
中心势是网络整体结构指标,反映了港口竞合网络的“紧凑程度”,记为CD,即
 |
(5) |
式中:CD(P*) 表示最大的节点度数中心度。
3) 接近中心度。
港口竞合网络中节点的接近中心度 (closeness centrality) 是指港口节点与竞合网络中其他港口的捷径距离之和,表明了港口节点到达其他港口节点要走的“步数”,计算公式为
 |
(6) |
式中:d(Pi, Pj) 为Pi到Pj的捷径长度。一般意义上来讲,与中心点距离越远的行动者在信息资源、权利、声望以及影响方面也越弱。注意,接近中心度的值越大,说明该点越不是网络的核心点。
在“合作”性质的网络中,港口节点的接近中心性表明,一个港口节点与其他点越接近这个节点在合作网络中传递信息就越方便。但是,在“竞争”关系性质的网络中,接近中心度的含义却截然相反。若某喂给港或支线港节点处在竞争关系网络的“核心”,从一定程度上说明了,该港口有着“定位不明确或过度竞争”的可能性。例如,在区域港口群的腹地范围内,某一种货物的港口运输能力已经饱和,但某港口仍然盲目地投资扩张装卸这种货物的码头泊位,导致其与周边多个港口产生了直接或间接的竞争关系,造成了市场产能过剩。这种情况不但浪费了企业资源,还可能造成市场内的恶性低价竞争。
4) 特征向量中心性。
特征向量中心性表明,如果一个港口节点与很多具有较高中心度的港口相连接,其重要程度就会很高[14]。
 |
(7) |
特征向量中心性可以认为是度中心性的改进,具有较高特征向量中心性的港口节点连接了更多的重要节点,系统地位最为突出,信息交互能力最强。
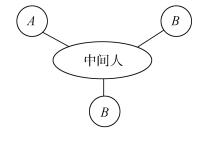
2.2.3 结构洞分析结构洞是由社会学家Burt[15]提出的,用来表示两个行动者之间非冗余的联系。一个结构洞中的“中间人”有着更强的“信息利益”和“控制利益”,因此比其他位置上的成员更具有竞争优势[16],如图 1所示。在Burt的结构洞指标中,限制度 (constraint) 指标最为重要[17],本文从限制度的指标出发,对区域港口群竞合网络进行结构洞分析。
|
| 图 1 结构洞示意图 Fig. 1 Schematic diagram of structural hole |
港口受到的限制度,是指该港口在竞合网络中拥有的运用结构洞的能力。根据Burt给出的限制度的操作化定义,港口Pi受到Pj的限制度指标为
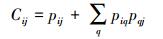 |
(8) |
式中:pij是指港口Pi为维持与港口Pj的关系所做的直接投入;q是除Rij之外所有的Pi到Pj的其他路径上的点;piq是在港口Pi的全部关系中,对q的投入所占比重。港口Pi受到Pj的限制度也可表述为Cij=直接投入+间接投入。
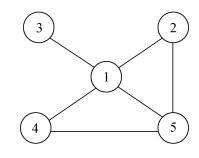
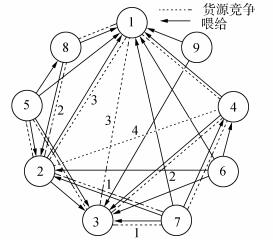
假设某区域港口群之间关系如图 2所示,以港口“1”为例,与之接触的港口“5”对港口“1”的限制最强,因为在港口“1”的相邻节点中,港口“5”与网络中其他成员之间的联系最多,“5”对“1”的要求将是“1”最难以回避的;而港口“3”对“1”的限制性最小,因为它与“1”的网络中的其他成员之间完全隔离。
|
| 图 2 限制度计算例图 Fig. 2 Case network for constrain calculation |
本文选取珠三角具有代表性的若干主要港口为例,对以上港口竞合网络分析模型进行实例研究,数据截至2015年最新数据,采用MATLAB编程实现。选取的港口包括香港、广州港、深圳港、珠海港、汕头港、佛山港、江门港、中山港、虎门港及惠州港。
3.1 珠三角港口群竞合网络构建港口群G={香港,广州,深圳,珠海,汕头,佛山,江门,中山,虎门,惠州}。港口群竞合网络物元、港口节点物元及港口竞合关系元在MATLAB程序中以数组的形式存在。
 |
其中包含了两个部分:1) 港口群网络的基本信息; 2) 港口群网络的结构信息,初始值为空值 (null)。
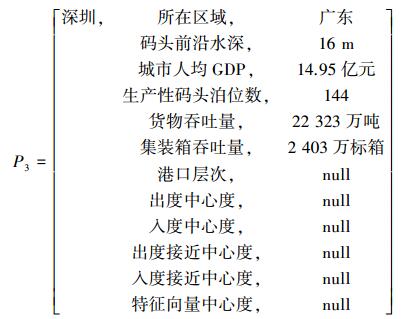
在珠江三角洲港口竞合网络的节点物元中,初始化存储了港口的一些基本信息,包括港口的所在省份 (区域),以及层次聚类分析会用到的相关特征及特征值;同时也包括了港口节点的结构信息,初始值为空值 (null)。部分初始港口物元如下所示:
 |
 |
 |
 |
以上数据来源《中国港口年鉴2015》及《中国统计年鉴2015》。
在珠江三角洲港口竞合网络关系元中,包含了港口之间竞争合作的关系数据。主要包括两个方面:一是港口之间的喂给合作,属于有向连接,使用0(无喂给) 或1(有喂给) 表示,前项为枢纽港,后向为喂给港;二是港口之间的同货类竞争,无向连接,由港口与货类之间的2-模隶属关系矩阵转换而来[18](使用ucinet[19]软件实现,具体过程此处不做赘述)。另外,关系元中还包含着港口限制度分析的结果。部分初始港口竞合关系元为
 |
 |
以上数据来源:调研数据;各港区官网货运业务及航线网络数据统计。
得到了港口节点物元及竞合网络关系元,根据社会网络的基元网表示方法[6],区域港口群竞合基元网络的表示如图 3所示。
|
| 图 3 区域港口群竞合基元网络 Fig. 3 Basic-element network for the regional port group |
利用MATLAB编程实现Ward法聚类过程,聚类循环中间结果如表 1所示,聚类过程谱系图如图 4所示。
| 聚类循环 | 合并的聚类 | 离差平方和 |
| 1 | 6、9 | 334.267 |
| 2 | 5、6 | 927.654 |
| 3 | 4、8 | 2 029.500 |
| 4 | 5、7 | 3 297.779 |
| 5 | 1、3 | 7 022.134 |
| 6 | 4、5 | 12 827.719 |
| 7 | 1、2 | 27 631.511 |
| 8 | 1、4 | 64 248.059 |

|
| 图 4 聚类过程谱系图 Fig. 4 Tree diagram of the clustering |
选取截断点,将珠三角港口竞合网络分为如下4个层次。
1) 综合枢纽港:广州港。广州港历史悠久,是我国沿海主枢纽港之一。广州港向内沟通珠三角纵横的河道交通;向外邻接港澳,辐射东南亚,连通世界各地,是珠三角区域港口群中功能最全的综合枢纽港。
2) 国际集装箱枢纽港:香港,深圳港。深圳港是全球最有效益的港口之一,已连续3年稳居世界第三大集装箱港口,也是珠三角产业区最主要的集装箱枢纽港;香港是中国天然良港,是远东的航运中心,也是全球最繁忙和最高效率的国际集装箱港口之一,是全球供应链上的主要枢纽港。
3) 国内沿海支线港:珠海港,虎门港。珠海港位于珠三角西部支线入海口,毗邻香港,接壤澳门。珠海港通过牵头建立西江港口联盟,与西南地区广大腹地建立了紧密的联系。虎门港是珠江口东岸的沿海支线港,处于广州—东莞—深圳—香港经济发展带与广州—佛山—中山—珠海经济发展带A字型框架的重要连接点上。
4) 喂给港:中山港,汕头港,惠州港,佛山港。中山等港口地处产业腹地的内河沿线,主要承担对枢纽港或支线港的喂给职能。
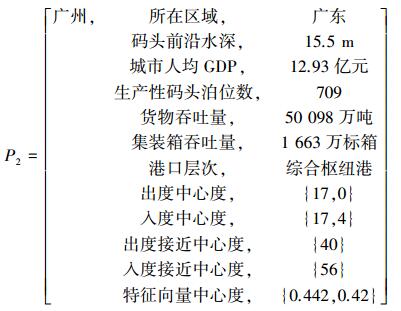
根据层次分析结果,可在港口节点物元中添加“网络层次”特征及特征值。以广州港为例:
 |
1) 网络密度分析。
针对珠三角港口群中港口的两种竞合关系,即“喂给关系”和“同货类竞争关系”,根据港口竞合关系元数据,进行计算分析。并相应更改网络物元中网络密度的值。
 |
根据Wellman (1979)[20]的研究,多数情况下,社会网络是“稀疏的”,即网络密度低。现实的社会网络中,47.1%的网络密度小于0.25。由此可以看出,珠三角港口群内部,无论是喂给合作网络,还是竞争关系网络,网络的密度都大于0.25,港口之间的竞争合作互动相对频繁。这与珠三角经济活动活跃,港口间距离较近有很大的关系。
2) 中心性分析。
接下来进行珠三角港口群竞合关系的中心性分析,并相应更新网络物元及港口节点物元的特征值,以网络物元及广州港为例:
 |
 |
所有港口节点分析结果总体如表 2所示。
| 节点物元 | 港口对象 | 网络层次 | 同货类竞争 | 喂给关系 | ||||||
| 度数 中心度 |
特征向量 中心度 |
出度 中心度 |
入度 中心度 |
出度接近 中心度 |
入度接近 中心度 |
特征向量 中心度 |
||||
| P1 | 香港 | 2 | 13 | 0.334 | 0 | 7 | 16 | 72 | 0.439 | |
| P2 | 广州 | 1 | 17 | 0.442 | 2 | 4 | 40 | 56 | 0.42 | |
| P3 | 深圳 | 2 | 16 | 0.418 | 0 | 6 | 17 | 72 | 0.399 | |
| P4 | 珠海 | 3 | 16 | 0.418 | 2 | 2 | 56 | 56 | 0.324 | |
| P5 | 汕头 | 4 | 8 | 0.199 | 3 | 0 | 72 | 48 | 0.269 | |
| P6 | 佛山 | 4 | 8 | 0.199 | 4 | 0 | 72 | 40 | 0.338 | |
| P7 | 中山 | 4 | 8 | 0.199 | 4 | 0 | 72 | 40 | 0.338 | |
| P8 | 虎门 | 3 | 13 | 0.334 | 2 | 0 | 72 | 49 | 0.184 | |
| P9 | 惠州 | 4 | 13 | 0.334 | 2 | 0 | 72 | 56 | 0.179 | |
| — | 中心势 | — | 18.3% | 30.15% | 26.56%(出度) | — | — | — | 28.91% | |
| 分析结果 | 68.75%(入度) | — | ||||||||
以上分析结果表明:首先,针对同货类竞争关系网络,度数中心度与特征向量中心度保持一致,充分体现了广州港处于珠三角港口竞合的“中心”;其次,我们很容易注意到处于第3、第4港口层次的虎门港、惠州港却有着与支线港、喂给港角色不符的高中心度,这与虎门港、惠州港自身“综合型”港口的定位有着很大的关系。但在当前航运市场,港口群整体竞争力的重要性远远超越港口本身能力,此时更应该考虑以“准确定位,分工明确”作为港口建设的方向。
从喂给关系网络的角度看,香港是当之无愧的珠三角港口群航运中心,在网络中地位最为突出,信息交互能力最强,而深圳港同样具有很高的枢纽港地位。并且,从数据可以看出,珠三角区域港口已形成了层次分明,枢纽港、支线港与喂给港分工明确的局势。
3) 结构洞分析。
结构洞分析主要针对港口的喂给关系网络。分析结果为港口Pi受到Pj的“限制度”关系,并将其存储于港口竞合关系元中。以关系元R12(广州—香港) 及R13(深圳—香港) 为例,添加限制度后的关系如下所示:
 |
 |
从结果 (表 3) 中可以找出对每个港口限制最大的港口。从喂给关系角度来看,广州港与香港的相互限制比较明显 (C12和C21),主要是由于广州港本身的枢纽港同时还承担着为香港喂给的功能;深圳港受广州港限制最大 (C32),主要是由于随着广州港南沙港区的投产,广州港集装箱吞吐量大幅增长,广深两港之间对集装箱货源的竞争更加激烈;而其他支线港及喂给港主要受其被喂给港口的限制,处于比较被动的状态,尤其是汕头港对广州港的依赖性极大 (C62=0.444)。
| 香港 (P1) |
广州 (P2) |
深圳 (P3) |
珠海 (P4) |
佛山 (P5) |
汕头 (P6) |
中山 (P7) |
虎门 (P8) |
惠州 (P9) |
|
| 香港 (P1) | 0.000 | 0.145 | 0.000 | 0.057 | 0.048 | 0.029 | 0.048 | 0.029 | 0.020 |
| 广州 (P2) | 0.174 | 0.000 | 0.111 | 0.000 | 0.058 | 0.058 | 0.058 | 0.040 | 0.000 |
| 深圳 (P3) | 0.000 | 0.130 | 0.000 | 0.077 | 0.070 | 0.043 | 0.070 | 0.000 | 0.028 |
| 珠海 (P4) | 0.174 | 0.000 | 0.174 | 0.000 | 0.174 | 0.000 | 0.174 | 0.000 | 0.000 |
| 佛山 (P5) | 0.174 | 0.174 | 0.174 | 0.174 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 汕头 (P6) | 0.198 | 0.444 | 0.198 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 中山 (P7) | 0.174 | 0.174 | 0.174 | 0.174 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 虎门 (P8) | 0.563 | 0.563 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 惠州 (P9) | 0.250 | 0.000 | 0.250 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
3.2.3 分析结果可视化
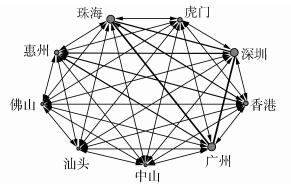
为了更直观地呈现港口竞合网络,使用Netdraw[21]生成珠三角港口群喂给关系及货源竞争关系网络社群图,如图 5和图 6所示。

|
| 图 5 珠三角港口群港口喂给关系社群图 Fig. 5 Sociogram of the feeding network for the port group in Pearl River Delta. |
|
| 图 6 珠三角港口群竞争关系社群图 Fig. 6 Sociogram of the competition network for the port group in Pearl River Delta. |
根据喂给关系中港口节点的入度 (被喂给),我们调整了喂给社群图中的节点大小,直观地可以看到,珠三角主枢纽港包括香港、深圳和广州。
在货源竞争关系图中,根据竞争关系的权值,调整了关系连线的宽度,我们可以明显地看出各港口之间的竞争关系强度的不同。同理,还可以根据其他分析结果调整社群图的节点、线条的大小及颜色等属性以便于更直观地观察网络的属性。
4 结论本文在创新的多维基元网络理论的基础之上,通过定义“港口群网络物元” “港口节点物元”及“港口竞合关系元”构建了区域港口群竞合网络。在此基础之上,利用网络层次聚类,网络密度、中心性及结构洞等网络分析方法,深入剖析港口节点在整个港口群竞合网络系统中所处的层次、地位、角色等社会属性。结合珠三角港口群竞合网络实例,进一步研究了港口节点的社会属性与节点间的竞合关系特征是否相符,从而反映出该港口竞合策略是否有利于形成良性的网络竞合关系局面。最后,从建立层次分明、定位明确、合理分工的良性港口群竞合关系网络的角度,对港口发展提出若干建议。结合实例分析,我们还得到区域港口群竞合网络的结构及社会属性特征:
1) 港口群系统一般存在层次结构,且港口“核心”程度基本与其港口层次保持一致;
2) 珠三角港口群港口之间竞争合作关系密切;
3) 在竞争性质的网络中,若低层次港口具有过高中心性,则该港口很有可能存在定位不明确或过度竞争的可能;
4) 喂给港的限制主要来自被喂给港;
5) 若中心度高的枢纽港对其他港口进行喂给,则将会对该港口形成较强的限制。
| [1] | AHUJA G. Collaboration networks, structural holes, and innovation: a longitudinal study[J]. Administrative science quarterly, 2000, 45(3): 425-455. DOI:10.2307/2667105. |
| [2] | NEWMAN M E J. The structure and function of complex networks[J]. SIAM review, 2003, 45(2): 167-256. DOI:10.1137/S003614450342480. |
| [3] | NEWMAN M E J. Scientific collaboration networks. I. Network construction and fundamental results[J]. Physical review E, 2001, 64(1): 016131. DOI:10.1103/PhysRevE.64.016131. |
| [4] | 李珊珊, 刘巍, 高红. 基于可拓基元理论的复杂社会网络分析模型[J]. 科技导报, 2014, 32 (36): 21-25. |
| [5] | 刘巍, 张秀芳. 基于可拓信息的知识表示[J]. 系统工程理论与实践, 1998 (1): 104-107. |
| [6] | 杨春燕, 李志明. 基于可拓学的社会网络结构研究[J]. 广东工业大学学报, 2014, 31 (1): 1-6. |
| [7] | MALCHOW M, KANAFANI A. A disaggregate analysis of factors influencing port selection[J]. Maritime policy & management: the flagship journal of international shipping and port research, 2001, 28(3): 265-277. |
| [8] | 杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014. |
| [9] | 徐敏杰. 集装箱港口网络的层系化分析与启示[J]. 中国航海, 2012, 35 (2): 106-109. |
| [10] | DEMATTEI C, MOLINARI N, DAUR S J P. Arbitrarily shaped multiple spatial cluster detection fore case event data[J]. Computational statistics & data analysis, 2007, 51(8): 3931-3945. |
| [11] | BOCCALETTI S, LATORA V, MORENO Y, et al. Complex networks: structure and dynamics[J]. Physics reports, 2006, 424(4/5): 175-308. |
| [12] | 刘军. 社会网络分析导论[M]. 北京: 社会科学文献出版社, 2004. |
| [13] | LAMBIOTTE R, AUSLOOS M, HOŁYST J A. Majority model on a network with communities[J]. Physical reviewe, 2007, 75(3): 030101. |
| [14] | 罗家德. 社会网分析讲义[M]. 2版. 北京: 社会科学文献出版社, 2010. |
| [15] | BURT R S. Structural holes: the social structure of competition[M]. New York: Cambridge University Press, 1995. |
| [16] | AHUJA G. Collaboration networks, structural holes, and innovation: a longitudinal study[J]. Administrative science quarterly, 2000, 45(3): 425-455. DOI:10.2307/2667105. |
| [17] | 刘军. 整体网分析讲义: UCINET软件实用指南[M]. 上海: 格致出版社, 2009. |
| [18] | SCOTT J. Social network analysis: a handbook[M]. 2nd ed. New York: SAGE Publications, 2000. |
| [19] | BORGATTI S P, EVERETT M G, FREEMAN L C. UCINET6 for windows software for social network analysis[P]. Harvard: Analytic Technologies, 2002. |
| [20] | WELLMAN B. The community question: the intimate networks of east Yorkers[J]. American journal of sociology, 1979, 84(5): 1201-1231. DOI:10.1086/226906. |
| [21] | BORGATTI S P. NetDraw: graph visualization software[Z]. Harvard: Analytic Technologies, 2002. |



