2. 石家庄铁道大学 信息科学与技术学院, 河北 石家庄 050043
2. School of Information Science and Technology, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
图像融合是信息融合的一个重要分支,其目的是将不同传感器获取的同一目标的互补信息合并为一幅新的具有更高可信度清晰度以及可理解性的图像[1]。因此,经过图像融合技术得到的合成图像可以更全面、更精确地描述所研究的对象,为进一步图像处理和分析提供高质量数据。因此,图像融合技术在军事、医学、遥感、计算机视觉等领域得到了广泛的应用[2]。一般来说,图像融合方法可以分为两类:空域融合方法和变换域融合方法。空域方法根据图像的清晰判别准则选择源图像中的像素,从而形成一幅融合后的图像。空域方法一般有空间频率(SF)、拉普拉斯能量(EOL)、修改拉普拉斯能量和(SML)等方法[3]。根据采用不同的变换,变换域方法可以分为小波变换、Contourlet变换、非子采样Contourlet变换以及Shearlet变换[4]等方法。
苗启广[5]提出了一种小波域基于区域局部能量的不同聚焦点图像融合方法,取得了很好的融合效果。传统的小波变换虽能高效处理和分析一维分段连续信号,但由一维小波通过张量积而形成的二维小波基不满足各向异性的尺度关系,小波变换无法精确地表述图像边缘信息,基于小波变换融合的图像容易产生细节成分模糊现象[6]。多小波能同时满足正交、紧支、对称等对信号处理十分重要的特性,被广泛应用于图像融合领域[7]。王迎春[8]在多小波变换域对低频和高频小波系数采用不同的融合方法,对低频系数采用取平均的方法,而对高频系数采用边缘梯度对比的方法。该方法能够很好保存图像的边缘和细节信息。但多小波是对传统的小波的扩展,仍不能解决类似于小波变换无法精确地表述图像边缘方向信息的问题。Cunha[9]提出的非子采样Contourlet变换(nonsubsampled contourlet transform,NSCT),由于同时具有灵活的多分辨率和多方向性表示的优点,相对小波变换来说,能够更好地表示图像的边缘信息。米德伶[10]对NSCT分解后的低频子带和高频方向子带分别以邻域梯度及合成邻域模值作为清晰度指标,采用自适应选择法实现对多聚焦图像的融合处理。然而,NSCT变换中的大量的冗余使得这些融合方法具有较高的时间复杂度。为了同时兼顾较小的分解冗余和分辨率多方向的优点,本文充分利用NSCT中非子采样方向滤波器组(nonsubsampled direction filter bank,NSDFB)能够更好捕捉图像的边缘的优点和Multiwavelet能同时满足正交、紧支、对称的特点,将Multiwavelet和NSDFB结合构建MNSDFB(multiwavelet nonsubsampled direction filter bank)变换,并利用该变换进行图像融合。
除了变换方法外,融合规则对融合的效果也会产生重要影响。近年来,许多学者提出了各种边缘保持滤波方法:双边滤波、引导滤波、域变换滤波、Cost-volume filtering[11]等,这些边缘保持滤波能够很好地保持图像的边缘结构。其中Gastal[11]等提出的域变换递归滤波(domain transform recursive filter,DTRF)将图像中的二维曲线通过等距变换映射到五维空间中,并保持曲线上每个点之间的距离不变,通过自适应地改变输入信号,将滤波运算降到了一维上,使得域变换滤波计算复杂度不受相关参数影响,因此,DTRF在保持图像边缘的同时,具有实时性的优点。本文在提出的MNSDFB变换基础上,提出了结合修改空间频率的域变换递归滤波的多聚焦图像融合方法。
1 域变换递归滤波
Gastal[11]在域变换基础上提出了边缘保持平滑递归滤波器(DTRF),它的基本思路可以理解为先降低输入信号的维数再进行低维滤波。在五维空间中,一个边缘保持的平滑滤波可以定义成一个空间不变的核H,它的响应会随着像素点间距离的变化而变化,如果在某个低维空间中这些距离保持不变,那么核的响应也将保持不变,因而,达到了保留图像边缘的目的[11]。DTRF首先将输入信号I变换到变换域Ωω,随后,变换域信号由递归滤波器(recursive filter,RF)进行处理如下:
J[m]=(1-ab)I[m]+abJ[m-1]
(1)
$${\rm{ct}}\left( u \right) = \int\limits_0^u 1 + {{{\delta _s}} \over {{\delta _r}}}\left| {I'\left( x \right)} \right|{\rm{d}}x,u \in {\Omega _w}$$
(2)
2 融合方法 2.1 组合多小波与NSDFB变换
非子采样Contourlet变换中首先对图像进行非子采样塔式分解,然后进行非子采样方向分解(NSDFB),从而建立了图像的多尺度、多方向的表示。根据NSCT的想法,本文利用多小波将图像分解为一个低频系数和3个高频系数,然后利用NSDFB将4个高频系数进行NSDFB方向分解。低频系数可以再次进行多小波分解,并再次对产生的高频系数,并再次对高频系数进行NSDFB方向分解,从而建立图像的MNSDFB变换。该变换不仅有正交、紧支撑的特点,同时还具有多尺度和多方向的特点,可以对图像进行较好地稀疏表示,同时能够更完美地表示图像的边缘和细节信息。该变换的2尺度2方向的分解如图 1所示。
 |
| 图 1 MNSDFB分解过程Fig. 1 The Decomposition of MNSDFB |
改进拉普拉斯能量和(sum-modified-Laplacian,SML)是空间域内典型的清晰度评价指标[12],反映了图像的边缘特征,能恰当地表征图像的聚焦特性和清晰度。由于SML反映的是邻域窗口内像素的能量和,SML规则也能够体现局部区域内多个像素的综合特征。因此,本文在低频系数中采用SML规则。其中,拉普拉斯(modified-Laplacian,ML)定义为
MLl(i,j)=|2Cl(i,j)-Cl(i-1,j)-Cl(i+1,j)|+|2Cl(i,j)-Cl(i,j+1)-Cl(i,j+1)|
(3)
$${\rm{SM}}{{\rm{L}}^l}\left( {i,j} \right) = \sum\limits_{o = - O}^O {\sum\limits_{p = - P}^P {{{\left[ {{\rm{M}}{{\rm{L}}^l}\left( {i + o,j + p} \right)} \right]}^2}} } $$
(4)
$${M^l}\left( {i,j} \right) = \left\{ \matrix{
1, {\rm{SML}}_A^l\left( {i,j} \right) \ge {\rm{SML}}_B^l\left( {i,j} \right) \hfill \cr
0, {\rm{SML}}_A^l\left( {i,j} \right) < {\rm{SML}}_B^l\left( {i,j} \right) \hfill \cr} \right.$$
(5)
因此,可以根据决策图选择融合后的MNSDFB低频系数CFl(i,j):
$$C_F^l\left( {i,j} \right) = \left\{ \matrix{
C_A^l\left( {i,j} \right), {M^l}\left( {i,j} \right) = 1 \hfill \cr
C_B^l\left( {i,j} \right), {M^l}\left( {i,j} \right) = 0 \hfill \cr} \right.$$
(6)
2.3 高频系数融合规则
MNSDFB变换中的高频细节信息中包含着丰富的图像特征细节信息,高频信息中绝对值较大的系数对应着一些突变,如图像的边缘、纹理等重要特征信息。由于图像的特征信息不是由单一的像素所表征的,而是由这一区域的多个像素来表征和体现[13]。空间频率就是利用了相邻像素的特征来表示的行频率和列频率,来区分图像的清晰程度。然而,空间频率没有利用相邻像素间的方向信息,不能有效地区分图像的清晰区域和模糊区域。Das提出的MSF[14]综合利用了图像的方向信息,同时结合列频率和行频率来作为图像的显著性特征准则。相对于空间频率方法,MSF能更加有效地区分图像的清晰区域和模糊区域。图像空间频率的计算方法为
$${\rm{SF}}\left( {m,n} \right) = \sqrt {{1 \over {MN}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left[ {{{\left( {{I_{m,n}} - {I_{m,n - 1}}} \right)}^2} - {{\left( {{I_{m,n}} - {I_{m - 1,n}}} \right)}^2}} \right]} } } $$
(7)
$${\rm{DF}}\left( {m,n} \right) = \sqrt {{1 \over {MN}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left[ {{{\left( {{I_{m,n}} - {I_{m - 1,n - 1}}} \right)}^2} - {{\left( {{I_{m,n}} - {I_{m - 1,n - 1}}} \right)}^2}} \right]} } } $$
(8)
$${\rm{MSF}}\left( {m,n} \right) = \sqrt {{\rm{DF}}{{\left( {m,n} \right)}^2} + {\rm{SF}}{{\left( {m,n} \right)}^2}} $$
(9)
由于DTRF可以忽略空间域图像的纹理信息,使得图像中具有相似特征的像素连接成为相似像素值区域,可以更好分聚焦区域和模糊。因此,在图像的多尺度变换域可以利用变DTRF滤波器对MSF进行滤波,利用DTRF滤波器输出去生成更为接近理想状态的融合决策图。利用式(9)计算所提出的MNSDFB高频系数的MSF值,并将其作为DTRF滤波器的输入,可以得到:
Rh,k(i,j)=RF(MSFh,k(i,j))
(10)
$${M^{h,k}}\left( {i,j} \right) = \left\{ \matrix{
1, R_A^{h,k}\left( {i,j} \right) \ge R_B^{h,k}\left( {i,j} \right) \hfill \cr
0, R_A^{h,k}\left( {i,j} \right) < R_B^{h,k}\left( {i,j} \right) \hfill \cr} \right.$$
(11)
根据决策图选择融合后的系数CFh,k(i,j):
$$C_F^{h,k}\left( {i,j} \right) = \left\{ \matrix{
D_A^{h,k}\left( {i,j} \right), {M^{h,k}}\left( {i,j} \right) = 1 \hfill \cr
D_B^{h,k}\left( {i,j} \right), {M^{h,k}}\left( {i,j} \right) = 0 \hfill \cr} \right.$$
(12)
2.4 算法步骤
本文融合方法如图 2所示并描述如下:
1)将源图像A和B进行l尺度的Multiwavelet分解,得到包含多小波低频系数GlA(i,j)、GlB(i,j)和多小波高频系数GhA(i,j)、GhB(i,j)。
2)对GhA(i,j)和GhB(i,j)的3个高频系数进行NSDFB分解得到k方向子带系数CAh,k(i,j)和CBh,k(i,j),k为NSDFB分解的方向。
3)对低频系数和高频系数分别按照相应的融合规则选择系数得到融合后的系数CFl(i,j)和CFh,k(i,j)。
4)对融合后系数CFl(i,j)和CFh,k(i,j)进行反NSDFB变换得到融合后的多小波低频系数GFl(i,j)和高频系数GhF(i,j)。
5)对小波系数GFl(i,j)、GhF(i,j)进行反多小波变换(IGHM)得到融合后的图像F。
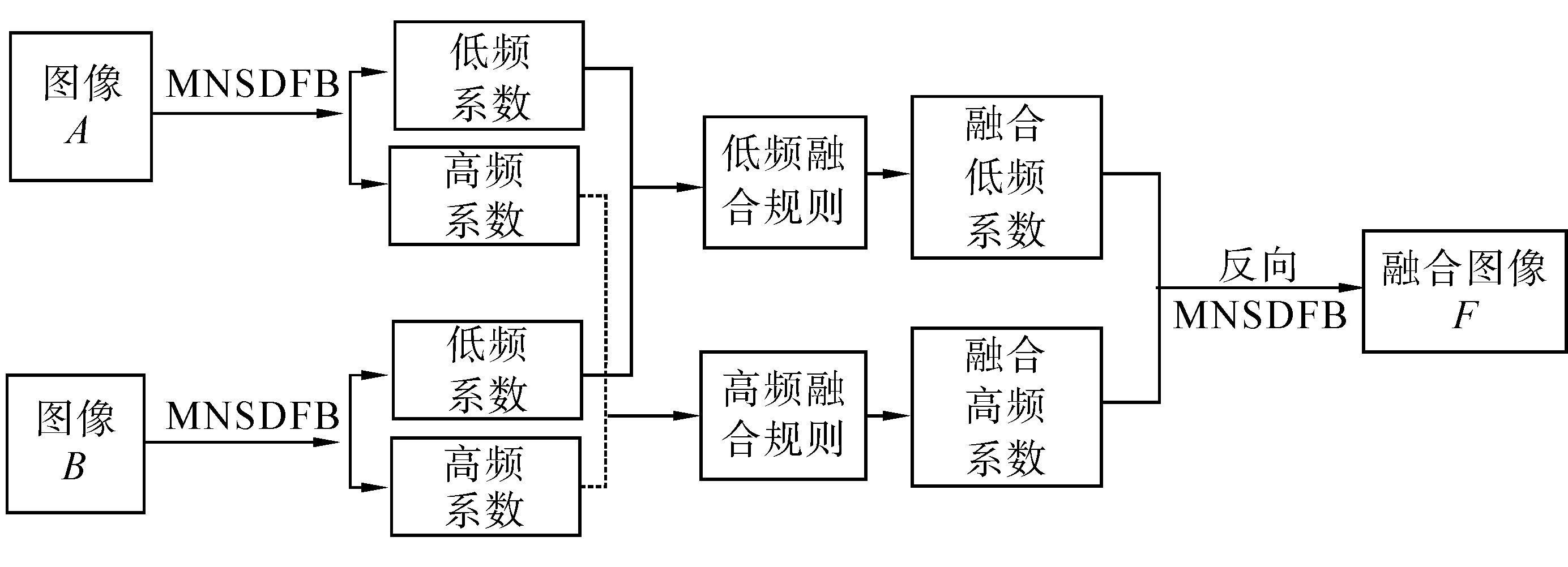 |
| 图 2 本文提出的融合方法Fig. 2 Proposed image method |
3 实验及结果分析
为验证本文算法的有效性与优越性,将本文提出方法与其他3种算法进行了多聚焦图像融合对比。1)Das[14]提出的采用MSF激发脉冲耦合神经网络(pulse couple neural network,PCNN)融合所有NSCT子带系数的方法。其中,非子采样方向滤波器设置为“cd”,金字塔滤波器采用“maxflat”滤波器,分解方向设置为[2 3 4 4];2)采用与第1种方法相同NSCT分解,融合规则采用修改的拉普拉斯能量和融合图像;3)Kumar提出的采用Cross bilateral filter的方法[15],本实验中采用和文献[15]完全相同的参数设置。本文提出方法采用2个尺度GHM的Multiwavelet分解,对每个高频多小波系数采用4方向NSDFB分解,低频系数采用SML融合规则,其他所有高频子带采用本文提出DTRF结合MSF的融合规则选择系数。图 3分别是进行融合测试的Clock、Lab、Disk、Pepsi 4对源多聚焦图像。
 |
| 图 3 第一组源多聚焦图像Fig. 3 The first group of source images |
Lab图像的融合结果如图 4(a)~(d)所示,对于人物头部区域来说,本文提出的方法具有更少的伪影信息,而其他3个方法的图像在该区域具有更为明显的伪影。对于Disk图像的融合结果来说,图 5(a)和图 5(b)中具有明显的伪影,而图 5(d)中出现了明显的边缘模糊现象,图 5(d)这些现象最为不明显;为了更为明显地展示不同方法的融合效果,图 4(e)~(h)和图 5(e)~(h)给出了不同方法获得的融合结果图像与源图像的残差图像。对于残差图像来说,更少的残差信息说明融合图像的相应区域绝大多数来自于源图像中清晰的部分,很少或者没有来自于另一幅源图像的模糊部分。图 4(e)和图 5(g)具有最为明显的残差信息,图 4(f)、图 4(g)、图 5(e)和图 5(f)的残差虽不太明显,但依然比图 4(h)和图 5(h)要明显得多。图 4(h)和图 5(h)几乎没有残留信息。以上分析表明:本文提出的融合方法相对于其他3种方法,能够获得更多来自源多聚焦图像中的聚焦良好区域的图像信息,同时引入了更少的伪影信息。
除了主观的视觉评价外,本文采用互信息(Mutual information,MI)、QAB/F[16]对融合结果进行客观评价,MI和QAB/F这两个指标并不要求知道理想的融合图像(也称为参考图像),并且大量的应用在图像融合客观评价中[17, 18]。MI也称为相关熵,用来评价源图像与融合图像之间的相似度,互信息值越大,说明融合的效果越好;QAB/F利用Sobel边缘检测来衡量有多少源图像的边缘细节信息转移到了融合图像,QAB/F的值越大,说明融合的效果越好;表 1给出了4种融合方法得到融合图像的评价指标的计算结果。从表 1看,本文提出的方法对于4对多聚焦图像都取得了最高的MI和QAB/F值,这表明所提出方法的融合结果相对于其他3种方法来说,融合了更多源图像的信息。
| 图像 | 评价指标 | Das方法 | NSCT_SML | Kumar方法 | 本文方法 |
| Lab | MI | 7.747 8 | 7.635 1 | 7.477 4 | 8.120 8 |
| QAB/F | 0.718 3 | 0.733 8 | 0.732 1 | 0.741 6 | |
| Disk | MI | 7.202 2 | 6.851 0 | 6.673 5 | 7.761 2 |
| QAB/F | 0.699 2 | 0.713 9 | 0.695 0 | 0.718 4 | |
| Clock | MI | 7.220 5 | 7.449 6 | 7.413 9 | 7.785 5 |
| QAB/F | 0.647 7 | 0.674 3 | 0.687 3 | 0.688 9 | |
| Pepsi | MI | 7.726 0 | 7.401 7 | 7.228 2 | 7.513 5 |
| QAB/F | 0.759 2 | 0.776 8 | 0.779 8 | 0.782 5 |
 |
| 图 4 Lab图像融合实验Fig. 4 Image fusion experiment on Lab image |
 |
| 图 5 Disk图像融合实验Fig. 5 Image fusion experiment on Disk image |
由于MI和QAB/F这两种图像融合评价方法仅仅衡量融合中的信息量和边缘保留量。为了对融合结果图像的灰度失真、结构畸变等方面进行评估,本文另外采用了SSIM[19]和VIF[20]两个指标进行了客观评价。鉴于上述两个指标为有参考图像评价方法,利用了的Lena、Barbara、Peppers 3幅测试图像,对这3幅图像的左右两个部分分别进行高斯模糊,结果如图 6所示。对图 6中3对源图像采用本文方法、Das方法和Kumar方法分别进行融合,融合结果的客观评价结果如表 2所示,由表 2可知,本文方法相对于另外两种方法来说,不仅MI和QAB/F这两个指标取得较大值,SSIM和VIF两个指标也得到最大值。
 |
| 图 6 第二组源多聚焦图像Fig. 6 The second group of source images |
| 图像 | 评价指标 | Das方法 | Kumar方法 | 本文方法 |
| Lena | SSIM | 0.987 5 | 0.987 9 | 0.991 3 |
| VIF | 0.933 4 | 0.894 9 | 0.945 9 | |
| MI | 5.995 3 | 6.283 2 | 6.531 0 | |
| QAB/F | 0.687 6 | 0.715 8 | 0.718 1 | |
| Barbara | SSIM | 0.995 7 | 0.996 6 | 0.998 7 |
| VIF | 0.977 0 | 0.958 8 | 0.992 6 | |
| MI | 6.285 9 | 6.614 4 | 6.747 3 | |
| QAB/F | 0.758 2 | 0.769 1 | 0.773 4 | |
| Peppers | SSIM | 0.994 0 | 0.993 5 | 0.994 1 |
| VIF | 0.971 2 | 0.943 1 | 0.977 5 | |
| MI | 6.785 9 | 7.080 1 | 7.443 2 | |
| QAB/F | 0.673 9 | 0.684 8 | 0.687 6 |
最后,表 3给出了本文提出的MNSDFB变换方法和NSCT方法在融合不同大小图像的运行时间对比,由于本文试验中所有源图像只有480×640、512×512两种尺寸。因此,本文只选择了Clock图像和Lab图像进行试验。对于上述两种融合方法来说,低频均采用了均值规则,高频均采用极大值规则。进行实验的计算机的CPU为四核2.5 GHz,内存为4 GB。实验结果表明,所提出MNSDFB变换方法相对于NSCT方法具有更快的运算速度。
综上所述,本文的算法得到的融合图像能够有效选择源图像中清晰区域的图像信息,对图像边缘以及细节信息表述得更为清晰突出,图像灰度失真和结构畸变较小,主观目视效果更好,并且也获得了最好的客观评价指标。
| s | |||
| 图像 | 尺寸 | NSCT方法 | 本文方法 |
| Clock | 512×512 | 34.73 | 24.74 |
| Lab | 480×640 | 36.20 | 25.54 |
图像的多尺度分解和融合规则是决定多聚焦图像融合结果的关键因素,本文利用多小波的高频子带系数进行NSDFB分解构建了MNSDFB变换,低频系数采用SML融合规则,高频系数采用域变换递归滤波器融合规则。实验结果表明:与NSCT变换改进空间频率激发PCNN的融合规则、NSCT变换采用SML的融合方法和Cross bilateral filter融合方法相比较,本文所提出的方法获取的融合图像保留丰富图像细节信息,获得了更好的视觉效果,并且采用互信息、QAB/F、SSIM、VIF等客观指标进行比较,取得了较好的客观融合评价结果。多小波和MNSDFB变换依然存在冗余问题,因此,如何减少本文提出方法的冗余度是未来的研究方向。
| [1] | BAI Xiangzhi, ZHANG Yu, ZHOU Fugen, et al. Quadtree-based multi-focus image fusion using a weighted focus-measure[J]. Information fusion, 2015, 22: 105-118. |
| [2] | 许良凤, 林辉, 胡敏. 基于差分进化算法的多模态医学图像融合[J]. 电子测量与仪器学, 2013, 27(2): 110-114.XU Liangfeng, LIN Hui, HU Min. Multi-modality medicine image fusion based on differential evolution algorithm[J]. Journal of electronic measurement and instrument, 2013, 27(2): 110-114. |
| [3] | 李华锋, 柴毅, 张晓阳. 提升静态小波域内多聚焦图像融合算法[J]. 光电工程, 2011, 38(3): 131-137, 144.LI Huafeng, CHAI Yi, ZHANG Xiaoyang. Multi-focus image fusion algorithm in lifting stationary wavelet domain[J]. Opto-electronic engineering, 2011, 38(3): 131-137, 144. |
| [4] | LIU Xuan, ZHOU Yue, WANG Jiajun. Image fusion based on shearlet transform and regional features[J]. AEU-international journal of electronics and communications, 2013, 68(6): 471-477. |
| [5] | 苗启广, 王宝树. 基于小波变换与局部能量的多聚焦图像融合[J]. 计算机科学, 2005, 32(2): 229-232.MIAO Qiguang, WANG Baoshu. Multi-focus image fusion based on wavelet transform and local energy[J]. Computer science, 2005, 32(2): 229-232. |
| [6] | 宗思光, 王江安. 多尺度形态算子融合图像滤波技术及滤波质量评价[J]. 光学学报, 2005, 25(9): 1176-1180.ZONG Siguang, WANG Jiang'an. Multi-scale mathematical morphology fusion filtering and the evaluation of the filtered image[J]. Acta optica sinica, 2005, 25(9): 1176-1180. |
| [7] | WANG Zhihui, ZHAO Baojun, SHEN Tingzhi. Image fusion based on multiwavelet transformation and PCNN[J]. Journal of information & computational science, 2008, 5(3): 1397-1406. |
| [8] | 朱四荣, 王迎春. 基于多小波变换的多聚焦图像融合[J]. 计算机工程与应用, 2010, 46(6): 169-170, 226. ZHU Sirong, WANG Yingchun. Multi-focus image fusion method based on multi-wavelet transform[J]. Computer engineering and applications, 2010, 46(6): 169-170, 226. |
| [9] | DA CUNHA A L, ZHOU Jianping, DO M N. The nonsubsampled contourlet transform: Theory, design, and applications[J]. IEEE transactions on image processing, 2006, 15(10): 3089-3101. |
| [10] | 米德伶, 冯鹏, 魏彪, 等. 一种基于清晰度计算的NSCT域多聚焦图像融合算法[J]. 光学与光电技术, 2010, 8(2): 7-10. MI Deling, FENG Peng, WEI Biao, et al. A multi-focus image fusion algorithm based on the calculation of clarity in NSCT domain[J]. Optics & optoelectronic technology, 2010, 8(2): 7-10. |
| [11] | GASTAL E S L, OLIVEIRA M M. Domain transform for edge-aware image and video processing[J]. ACM transactions on graphics, 2011, 30(4): 69. |
| [12] | GENG Peng, HUANG Min, LIU Shuaiqi, et al. Multifocus image fusion method of Ripplet transform based on cycle spinning[J]. Multimedia tools and applications, 2014: 1-11, doi: 10.1007/s11042-014-1942-1. |
| [13] | 屈小波, 闫敬文, 杨贵德. 改进拉普拉斯能量和的尖锐频率局部化Contourlet域多聚焦图像融合方法[J]. 光学精密工程, 2009, 17(5): 1203-1212.QU Xiaobo, YAN Jingwen, YANG Guide. Multifocus image fusion method of sharp frequency localized Contourlet transform domain based on sum-modified-Laplacian[J]. Optics and precision engineering, 2009, 17(5): 1203-1212. |
| [14] | DAS S, KUNDU M K. NSCT-based multimodal medical image fusion using pulse-coupled neural network and modified spatial frequency[J]. Medical & biological engineering & computing, 2012, 50(10): 1105-1114. |
| [15] | KUMAR B K S. Image fusion based on pixel significance using cross bilateral filter[J]. Signal, image and video processing, 2015, 9(5): 1193-1204. |
| [16] | GANGAPURE V N, BANERJEE S, CHOWDHURY A S. Steerable local frequency based multispectral multifocus image fusion[J]. Information fusion, 2015, 23: 99-115. |
| [17] | 李俊峰, 姜晓丽, 戴文战. 基于提升小波变换的医学图像融合[J]. 中国图象图形学报, 2014, 19(11): 1639-1648. LI Junfeng, JIANG Xiaoli, DAI Wenzhan. Medical image fusion based on lifting wavelet transform[J]. Journal of image and graphics, 2014, 19(11): 1639-1648. |
| [18] | 高继森, 董亚楠, 沈瑜, 等. 基于改进Tetrolet变换的图像融合算法研究[J]. 计算机科学, 2015, 42(5): 320-323.GAO Jisen, DONG Yanan, SHEN Yu, et al. Research of image fusion algorithm based on improved Tetrolet transform[J]. Computer science, 2015, 42(5): 320-323. |
| [19] | WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE transactions on image processing, 2004, 13(4): 600-612. |
| [20] | SHEIKH H R, BOVIK A C. Image information and visual quality[J]. IEEE transactions on image processing, 2006, 15(2): 430-444. |



