1985年,Rumelhart把BP算法应用到神经网络的训练过程,提出了著名的“BP神经网络”。经过近30年的发展,针对经典BP算法存在的收敛慢、易陷入局部最优和分类泛化能力差等缺点,不同学者提出了很多改进学习方法。
在神经网络收敛速度慢的问题上提出的改进算法主要分为新型参数调整策略和新型学习方法两个方向。参数调整,即学习过程中动态地调整学习率、步长等学习参数来加速网络训练。主要改进方法包括:变学习率算法[1]、缩减学习率[2]、随机调整学习率[3]、弹性BP算法[4]、变梯度算法[5]等。新型学习方法主要是在BP算法的基础上借助优化理论和方法来加速网络收敛,如动量项算法[6]、具有高阶收敛特性的限域牛顿算法[7]、LM算法[8]等。在神经网络应用中分类泛化能力差的问题上,提出的改进算法主要包括:基于权值惩罚的方法[9]、GA等仿生优化算法和神经网络复合训练[10]方法等。以上改进方法各有所长,但是在收敛速度和泛化性能之间的平衡性问题上还存在着较大提升空间,寻求收敛速度快、泛化性能高的新型学习方法依然是BP神经网络研究领域中一个重要问题。
自2006年开始,有着更强表达能力的深度神经网络开始流行。由于网络结构复杂,数据规模大,为保证网络收敛和避免内存溢出,深度神经网络学习时普遍采用子批量学习方法。借鉴深度神经网络的学习方法,本文从学习批量的角度来探究批量对于浅层BP神经网络收敛速度和泛化能力的影响,提出了基于子批量神经网络学习方法,研究了学习率和学习批量对于网络收敛性和收敛速度的影响。
1 BP 神经网络学习方法BP算法由信号前馈传递和误差反向传递两阶段组成。信号前馈传递阶段,信号从输入节点先传向隐层节点,再传向输出层产生输出信号;误差反向传递阶段,依据标签数据和网络输出之间的误差,把误差逐层向前传播来调节网络权值,通过权值的不断修正使网络的实际输出更接近期望输出。网络训练过程中,根据权值更新执行方式的不同,神经网络学习方法可分为全批量学习(Off-line learning)和单批量学习(On-line learning)两种方法[11]。
设网络输入为x,输出为f(x),样本标签为y;训练样本总数为m,样本均值误差为E,连接权值为ω,学习率为α,则BP学习算法描述如下。
1.1 单批量学习单批量学习过程要求每个训练样本呈现给网络之后即刻更新权值,网络完成一次迭代,权值更新m次,主要算法步骤如下:
1)初始化网络结构,随机初始化网络权值。
2)计算网络单个样本误差ei:
| $${e_i} = {(f({x_i}) -{y_i})^2}$$ | (1) |
3)单个样本内修正网络权值:
| $${w_i}(k + 1) = {w_i}(k) + a{{\partial {e_i}} \over {\partial {w_i}}}$$ | (2) |
4)计算所有样本的均方误差:
| $$E = {1 \over m}\sum\limits_{i = 1}^m {{e_i}} $$ | (3) |
5)根据误差结果和迭代次数进行判断是否达到收敛要求,若达到要求则网络完成训练,否则循环2)~4)。
1.2 全批量学习全批量是在所有训练样本都呈现给神经网络之后,通过全样本的梯度均值来更新权值,网络完成一次迭代,权值只更新一次,主要算法步骤如下:
1)初始化网络结构,随机初始化网络权值。
2)计算网络批量均值误差:
| $$E = {1 \over m}\sum\limits_{i = 1}^m {{{(f({x_i}) - {y_i})}_2}} $$ | (4) |
3)批量内修正网络权值:
| $$w(k + 1) = w(k) + a{{\partial E} \over {\partial w}}$$ | (5) |
4)根据均方误差和迭代次数进行判断是否达到收敛要求,若达到要求则网络完成训练,否则循环2)~3)。
2 子批量学习方法及参数配置单批量学习方法网络完成一次迭代,权值更新m次,其优势是:能够从冗余性中获益,可以跟踪训练数据较小的改变;每次迭代权值更新次数多,收敛速度快。缺点在于:每个样本都需要完成一次权值更新计算2)~3),导致网络每次迭代计算时间较长,收敛时间较长;此外由于数据间的差异性和噪点的影响,导致权值更新时存在权值扰动,容易引起网络波动,不利于网络收敛。
全批量学习方法网络完成一次迭代,权值只更新一次,这样通过平均权值修正处理,具有对训练数据低通滤波的作用,避免由于数据间差异和噪点引起的权值扰动;其次全批量可以通过矢量化编程,借助矩阵运算的优势,来提升计算速度,每次迭代时间短。缺点在于全批量均值处理使梯度误差较小,网络收敛缓慢,且矢量化编程计算,对于内存要求高。
2.1 子批量学习方法对比全批量和单批量学习方法,全批量学习具有计算快速稳定的优点,缺点是对于内存需求大,收敛缓慢;单批量学习具有收敛快速、能够跟踪数据变化的优点,缺点是存在扰动、训练时间长。综合全批量和单批量的优缺点,本文提出了浅层神经网络子批量学习方法。
子批量学习方法介于单批量和全批量之间,计算过程中首先将训练样本平均分成多个子批量,在每个子批量内进行全批量网络权值更新,即每个子批量呈现给网络后进行权值更新,每次迭代计算权值更新多次。主要算法流程图如图 1所示。
 |
| 图 1 BP神经网络子批量学习方法流程图Fig. 1 Flow chart of sub-batch learning method |
子批量学习是在子批量内更新网络权值,每次迭代权值进行多次更新,这样子批量内更新权值可以借助矢量化编程来加速迭代计算且对内存需求较小,其次可以在均值平滑滤波和权值扰动之间达到一种平衡。因此,子批量学习既具有全批量学习通过平均处理、滤波平稳的优势,又融合了单批量学习更新次数多、收敛快的特点,同时克服了全批量平均处理后网络收敛缓慢、内存需求高和单批量学习网络波动的缺点。
2.2 子批量学习参数配置研究由式(2)和式(5)可以看出,网络权值的更新量由学习率和梯度共同决定,所以学习率对于网络的收敛速度有着关键性的影响,通过调整学习率可以调节网络权值的更新程度,在训练过程中,学习率过大会导致学习过程震荡,网络收敛困难,学习率过小,导致网络收敛缓慢,迭代时间长。因此经常调整学习率来加速网络训练。
子批量学习方法中,子批量学习使网络权值更新在均值平滑滤波和扰动之间达到一种平衡,不同的批量在均值平滑滤波和扰动之间有所侧重,小批量更侧重于增大扰动影响,大批量更侧重于加强均值平滑滤波效果,网络学习率会放大或缩小这种侧重,所以批量和学习率的配置,对于网络的收敛性和训练时间有着重要的影响。
3 数值实验本文以具有代表性的Seeds[12]、Waveform[13] 和Music[14]分类数据集为实验对象,通过实验,比较单批量、全批量和子批量学习方法收敛速度,揭示子批量和学习率对网络收敛速度、训练时间和分类泛化能力的影响。
3.1 Seeds数据集分类实验Seeds数据集是由UCI提供的用于分类算法测试的实验数据集之一,该数据记录了3类种子的7种特征数据,总计210个样本。实验从3个类别中分别随机抽取36个样本组成训练集,剩余样本组成测试集。网络隐层节点个数设置为10,选取批量s为1、4、9、18、54、108,其中s=1为单批量学习,s=108为全批量学习,中间为不同批量大小的子批量学习方法,在相同网络初始权值下取20次实验的平均结果作为讨论对象。
3.1.1 不同批量收敛性研究为了探究批量对于网络收敛性的影响,实验在迭代5 000次情况下,不同批量网络性如图 2所示。
 |
| 图 2Seeds数据集不同批量下均值误差Fig. 2 MSE of seeds under different batch size |
由图 2,在相同的学习率情况下,批量越小,均值误差收敛越快,收敛所需要的迭代次数越小,但较小的批量,导致网络波动较大,存在随机扰动,如图 2中下方s=18,s=4时的曲线,误差曲线波动收敛;随着批量增大,均值误差收敛曲线扰动逐渐减小,收敛曲线逐渐平滑,这说明均值误差梯度起到了平滑滤波的效果;但误差曲线缓慢收敛,收敛所需要的迭代次数较大,如图 2中上方s=54,s=108时的曲线。
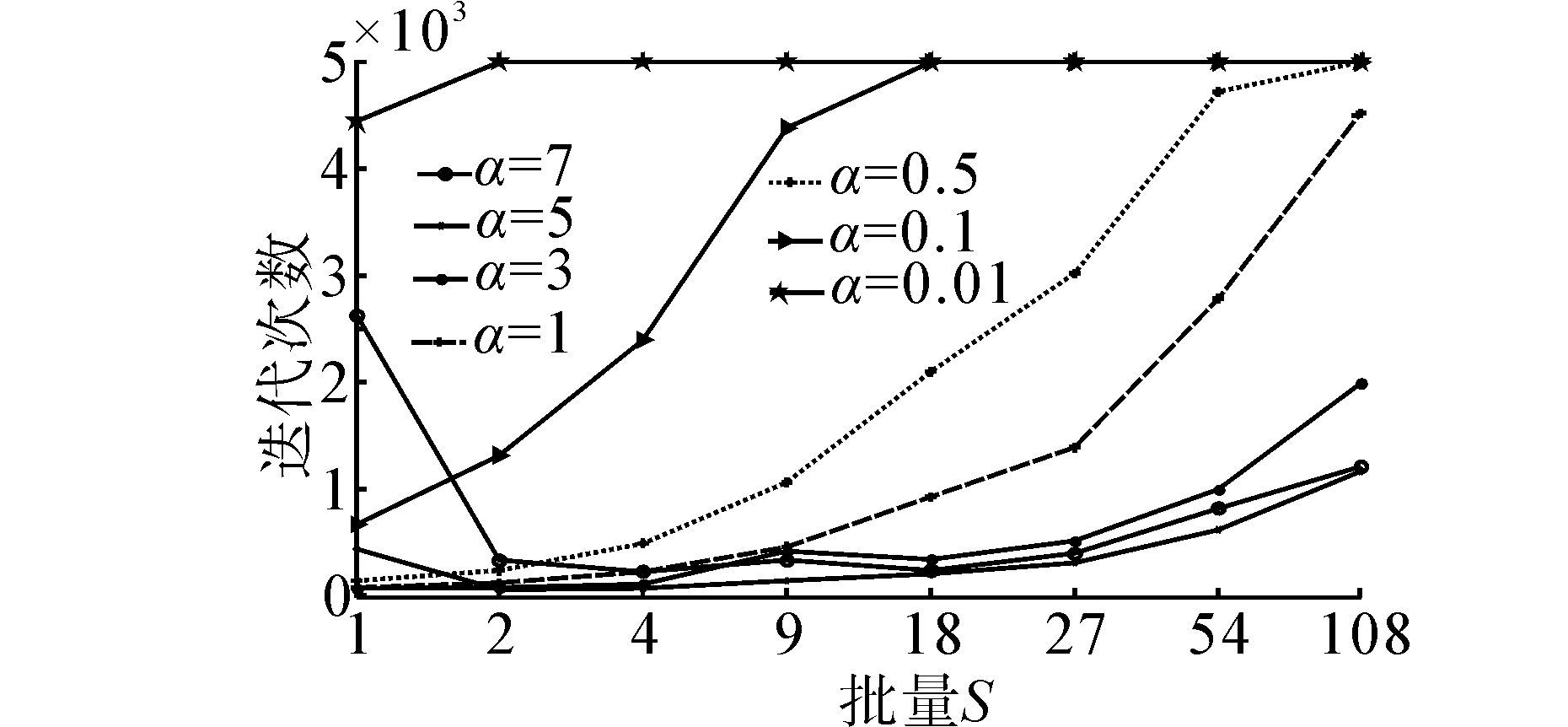
3.1.2 Seeds数据集迭代次数比较分析学习率是影响网络收敛性和训练时间的关键因素,在上述实验基础上,实验以E=0.005为收敛目标,迭代5 000次,分别在α=7、5、3、1、0.5、0.1、0.01总计7个不同的学习率下,测试不同学习率和批量对于网络迭代次数(图 3)、训练时间(表 1)和分类错误率(图 4)的影响。(实验验证在E=0.01时存在欠拟合,在E=0.001和E=0.000 5时存在过拟合。)
 |
| 图 3Seeds数据集不同批量下均值误差Fig. 3 MSE of seeds under different batch size |
| α | 1 | 2 | 4 | 9 | 18 | 27 | 54 | 108 |
| 0.01 | 86.75 | 50.11 | 25.78 | 12.21 | 6.74 | 4.82 | 2.92 | 2.03 |
| 0.1 | 10.83 | 11.35 | 11.39 | 11.00 | 6.91 | 4.98 | 3.00 | 2.10 |
| 0.5 | 2.13 | 2.04 | 2.12 | 2.24 | 2.50 | 2.76 | 2.68 | 1.95 |
| 1 | 1.19 | 1.02 | 1.00 | 1.07 | 1.18 | 1.26 | 1.54 | 1.84 |
| 3 | 1.15 | 0.52 | 0.37 | 0.41 | 0.42 | 0.43 | 0.52 | 0.72 |
| 5 | 3.55 | 0.49 | 0.24 | 0.24 | 0.20 | 0.22 | 0.26 | 0.37 |
| 7 | 48.39 | 0.76 | 0.27 | 0.20 | 0.23 | 0.19 | 0.22 | 0.33 |
 |
| 图 4Seeds数据集不同学习率和批量下错误率Fig. 4 Error rates of seeds under different learning rates and batch size |
1) 依据图 3,学习率相同时,网络首先在小批量上达到收敛,之后逐渐在所有批量上都达到收敛,随着批量增加,在不引起较大波动的情况下,网络收敛所需的迭代次数也逐渐增加,说明小批量对比大批量学习具有较快的收敛速度。
2) 当学习率过大,批量较小时,会引起网络波动,从而导致收敛迭代次数增大,如α=7,s=1时,迭代2 500次才收敛,而批量较大时则不会引起波动现象,说明大批量具有一定的稳定性,可以使网络平稳收敛。
这是由于数据之间即存在相似性又存在差异性所造成的,在利用子批量进行训练时,由于每个批量的数据样本都不同,当批量较小时,这种数据差异性凸显,所以每次迭代更新权值会有差别,即引起权值扰动;当学习率较小时,由于每次迭代的步长较小,这种扰动有利于网络探索到更小的均值误差值。其次,小批量下每次迭代,权值更新次数多,所以网络收敛迅速,但当学习率较大时,由于每次迭代步长较大,会导致这种数据扰动增大,从而造成矫枉过正,导致在大的学习率下,小批量学习使网络很难收敛。当批量较大时,梯度误差通过批量均值后,会产生类似平滑滤波的效果,这种平滑的效果抑制或减弱数据的差异性,凸显数据的相似性;随着批量的增大,这种平滑效果也增大,导致梯度误差和步长逐渐减小,使网络缓慢平稳收敛;所以当学习率较大时,大的批量依然能够确保网络快速稳定收敛,而不会引起网络发散。
所以选择适合的批量大小,会在数据的相似性和差异性,以及扰动和平滑之间达到一种平衡效果,适度利用扰动和平滑,保证在平稳的前提下,使网络最快达到收敛。
3.1.3 Seeds数据集训练时间分析1) 依据表 1,当学习率过小,如α=0.01时,网络收敛速度较慢,导致网络在s>1时,迭代5 000次的情况下都未达到收敛,但在迭代次数相同的情况下,随着批量的增大,凭借矩阵运算快速的优势,网络训练时间呈指数级减小,所以子批量学习可以大幅减少每次迭代计算时间。
2) 相同批量下,网络收敛时间并没有随着学习率的增大而逐渐减小。当批量s<18时,随着学习率的增大,网络的收敛时间呈现先减小后增大的趋势,这是由于小批量下存在误差权值的扰动,在小的学习率下这种扰动有利于网络学习,但这种扰动随着学习率的增大,导致每次批量更新权值过度扰动,从而使网络收敛困难,收敛所需迭代次数增多,网络训练时间增加。
3) 相同学习率下,随着批量的增大,网络的训练时间也呈现先减小后增大的趋势,这是由于随着批量的增大,基于均值的权值更新方法逐渐抑制扰动的同时,平滑滤波效果也逐渐增强,适合的批量,使扰动抑制和平滑效果最佳,使网络最快收敛。
3.1.4 Seeds数据集错误率分析依据图 4,忽略α=0.01时,网络不收敛的情况,相同学习率下,批量对于网络的分类泛化能力,有着一定的影响。综合不同学习率,错误率在批量较小时波动较大,批量较大时,错误率波动较小。这是由于批量较小时,权值更新扰动明显,这种扰动可以使网络探索更多的权值空间,随着批量的增大,权值扰动逐渐被抑制,所以批量较小时网络错误率波动较大,批量较大时网络错误率波动较小。对比不同学习率下最小错误率,发现不同的学习率对应不同的最优批量,对应关系如表 2所示。
| 学习率 | 0.01 | 0.1 | 0.5 | 1 | 3 | 5 | 7 |
| 最优批量 | 1 | 2 | 4 | 9 | 108 | 54,108 | 54 |
| 错误率/% | 6.76 | 5.05 | 5.78 | 6.18 | 5.20 | 5.83 | 5.44 |
依据表 2,随着学习率的增大,网络对应的最优批量也随之增大,对比小批量下的错误率,网络在较大的批量处取得较小的分类错误率,这是由于Seeds数据集数据之间的相似性较高,在大的批量下平滑滤波更适合相似性较高数据集,小批量下的随机扰动则不适合数据相似性较高的数据集。
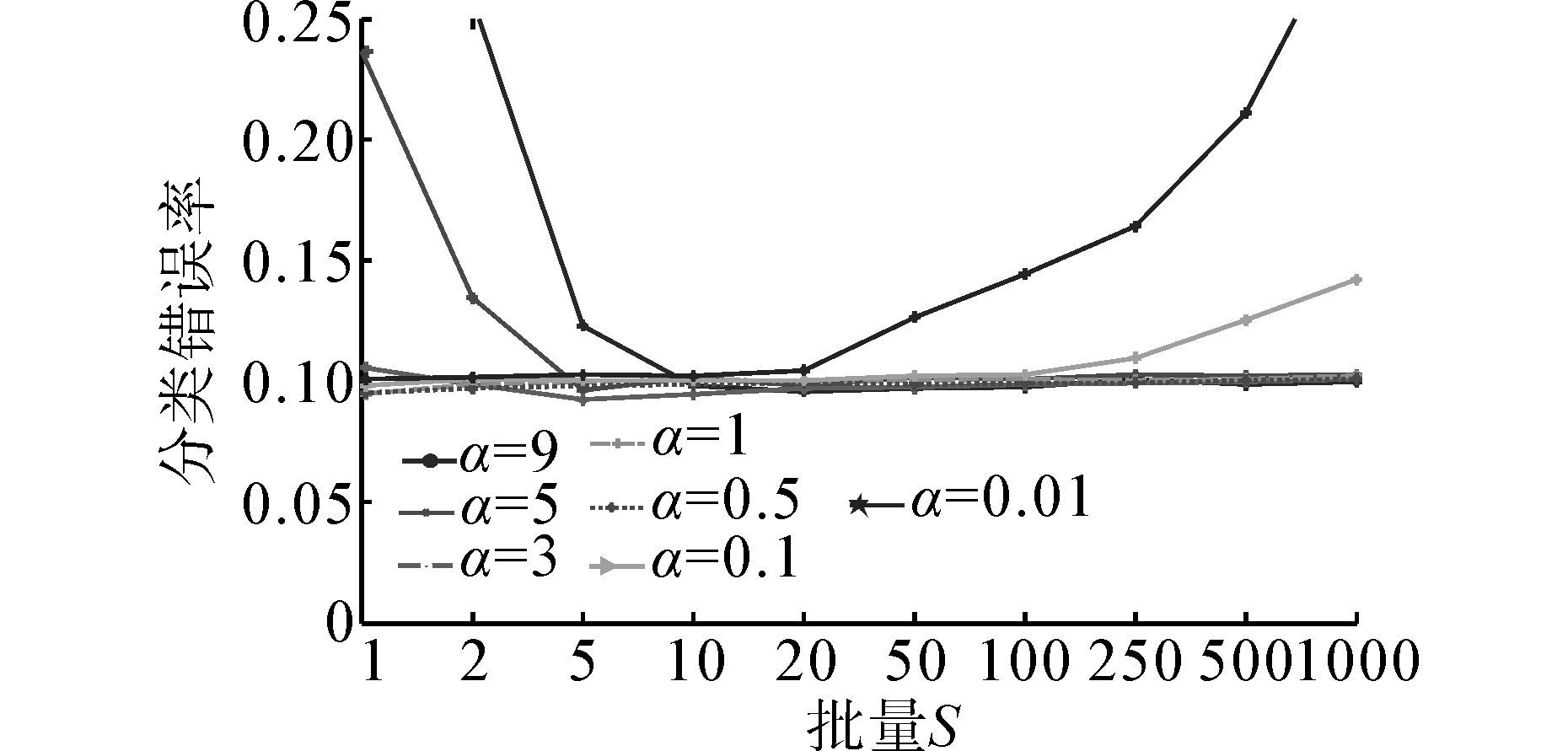
3.2 Music分类实验Music数据集通过倒谱系数法提取4种音乐类型总计500组24维的音素特征。实验在每类音乐随机抽取250个样本作为训练集,剩余样本为训练集。网络隐层节点为50,E=0.001,迭代5 000次,选取批量s为1、2、5、10、20、50、100、250、500、1 000,相同条件下,取20次实验的平均结果作为讨论对象,来测试学习率和批量对于网络迭代次数(图 5)、训练时间(表 3)和分类错误率(图 6)的影响。
 |
| 图 5Music数据集不同学习率和批量下的迭代次数Fig. 5 Converge epochs of music under different learning rates and batch size |
| α | 1 | 2 | 5 | 10 | 20 | 50 | 100 | 250 | 500 | 1 000 |
| 0.01 | 880 | 712 | 375 | 204 | 128 | 88 | 57 | 34 | 29 | 27 |
| 0.1 | 399 | 225 | 136 | 109 | 109 | 88 | 58 | 34 | 29 | 27 |
| 0.5 | 397 | 107 | 51 | 35 | 31 | 39 | 45 | 34 | 29 | 27 |
| 1 | 613 | 160 | 82 | 46 | 33 | 33 | 31 | 31 | 28 | 25 |
| 3 | 1 640 | 694 | 86 | 8 | 4 | 7 | 9 | 13 | 21 | 26 |
| 5 | 1 700 | 843 | 168 | 69 | 17 | 21 | 16 | 14 | 16 | 20 |
| 9 | 1 695 | 843 | 334 | 120 | 19 | 4 | 11 | 13 | 11 | 15 |
 |
| 图 6 Music数据集不同学习率和批量下的错误率Fig. 6 Error rates of music under different learning rates and batch size |
对比图 5和图 3可知,批量对Music数据集收敛迭代次数影响较大,随着批量增加,网络迭代次数呈现指数级别的先减小后增大的趋势。这是由于Music数据集样本容量大,数据间差异较大。相比Seeds数据集,当采用小批量训练时,批量间的权值更新扰动较大,由于随着学习率的增加,会放大这种扰动,所以Music数据集随着批量的变化,网络收敛所需的迭代次数呈现指数级别的减小。
由于Music数据集训练样本个数较多,随着批量的增加,会造成平滑过渡现象,使均值误差过小,从而使误差梯度较小,导致网络收敛缓慢,造成大批量训练网络需要较多的迭代次数。
3.2.2 Music数据集训练时间比较依据表 3,在收敛的条件下,批量对于Music数据集的训练时间影响较大,如最长收敛时间为880 s,最短收敛时间仅为4 s,差异较大。在相同学习率下随着批量的增加,训练时间呈现先减小后增大的趋势。相同批量下,随着学习率的增大,训练时间也呈现先减小后增大的趋势。这是由于批量学习可以通过矢量化编程来借助矩阵运算的优势来加快计算时间,而且批量越大,这种优势越明显,每次迭代所需的时间越小。但较大的批量会造成一定程度的过平滑,使网络收敛所需迭代次数增加,所以选择适合的批量,不但可以利用矩阵计算的优势,还不会导致过度平滑,从而大幅缩短网络训练时间。
3.2.3Music数据集分类准确率比较首先依据图 5,在批量小、学习率大和批量大、学习率小的情况下网络不收敛,所以图 6中网络未收敛时分类错误率较大。
在收敛的条件下,不同学习率和不同批量的分类效果存在一定的差别。对比图 6和图 4,Seeds数据集中大批量对应较小的分类错误率,而Music中小批量下取得较小的错误率,这是由于Music数据集中数据之间差异较大,而这种差异性导致分类错误率整体比Seeds数据集高,为了适应数据间的这种差异,需要探索更多的空间,而小批量下的随机扰动,可以使网络探索更多的空间,从而找到泛化能力更好的空间,提升网络的分类能力。所以对于Music这种数据间差异较大的数据集,在不考虑训练时间和迭代速度的情况下,使用小批量训练网络具有更好的泛化能力。
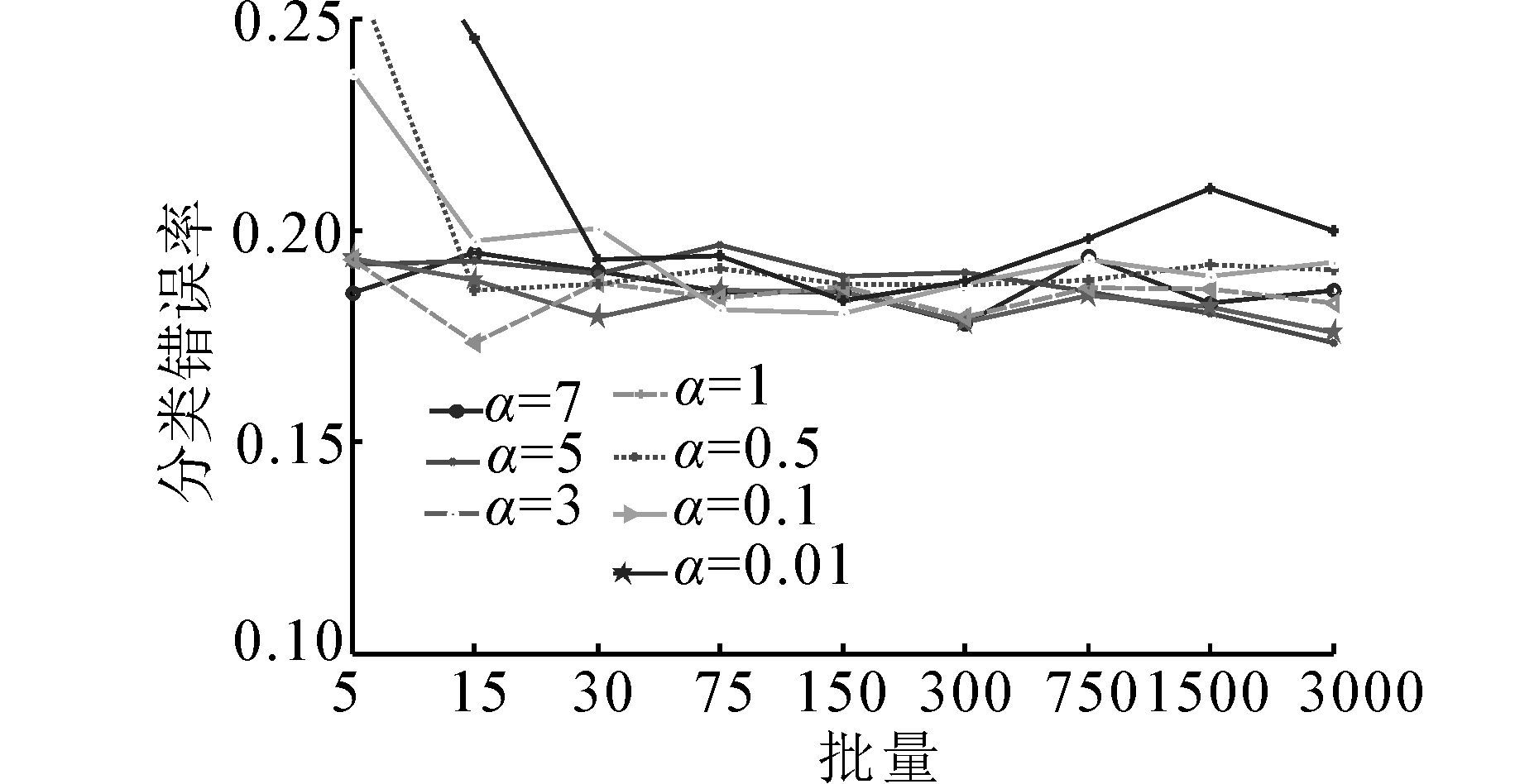
3.3 Waveform分类实验Waveform数据集由UCI提供的用于分类算法测试的实验数据集之一,该数据集包含5 000个样本的3分类数据集,实验在每个类别中随机抽取1 000个样本作为训练集,剩余2 000个样本为训练集。网络隐层节点为50,E=0.005,迭代8 000次,选取批量s为5、15、30、75、150、300、750、1 500、3 000,相同条件下,取10次实验的平均结果作为讨论对象,来测试学习率和批量对于训练时间(表 3)和分类错误率(图 6)的影响。
3.3.1 Waveform数据集训练时间比较依据表 4中不同学习率和批量下的网络训练时间,学习批量对Waveform数据集网络的收敛时间影响较大,说明批量和学习率可大幅减小大数据网络的训练时间。
| α | 5 | 15 | 30 | 75 | 150 | 300 | 750 | 1 500 | 3 000 |
| 0.01 | 81 | 87.0 | 105.1 | 82.9 | 61.4 | 50.3 | 40.5 | 39.6 | 37.5 |
| 0.05 | 155 | 22.5 | 25.2 | 40.9 | 53.5 | 47.8 | 37.8 | 35.7 | 32.8 |
| 0.1 | 1 109 | 14.1 | 12.9 | 19.7 | 28.8 | 37.7 | 39.0 | 36.3 | 33.4 |
| 0.5 | 1 101 | 307.4 | 150.7 | 7.4 | 12.4 | 12.8 | 23.8 | 33.7 | 35.1 |
| 1 | 1 173 | 325.2 | 160.1 | 65.4 | 14.0 | 7.7 | 21.7 | 24.4 | 29.9 |
| 3 | 1 312 | 3 42.4 | 166.4 | 84.6 | 60.9 | 50.0 | 39.8 | 38.1 | 34.9 |
| 7 | 4 009 | 428.0 | 193.0 | 90.1 | 64.0 | 52.4 | 41.5 | 39.1 | 35.0 |
综合对比表 1、3、4可发现学习率和训练批量对于网络的收敛性、收敛时间具有如下规律:
1)固定迭代次数下,当学习率小、批量大和学习率大、批量小的情况下,网络不收敛。前者是由于扰动较大导致网络不容易收敛造成,后者是由于过渡平滑导致网络收敛缓慢引起。
2)在收敛的情况下,批量保持稳定时,随着学习率的增大,网络训练时间呈现先减小后增大的趋势;学习率保持稳定时,随着批量的逐渐增大,网络训练时间也呈现先减小后增大的趋势。
3)选择最优的批量和学习率组合可以成倍地减小网络训练时间,而且数据集越大批量对网络收敛时间的影响越关键。 3.3.2 Waveform数据集分类准确率比较
依据图 7在收敛的条件下,不同学习率和批量的分类效果存在一定的差别,但差异较小。小批量和大批量下的网络分类误差结果相似,说明批量对于Waveform数据集网络的分类泛化能力影响较小。
 |
| 图 7Music数据集不同学习率和批量下的错误率Fig. 7 Error rates of Waveform under different learning rates and batch size |
综合对比图 4、6、7可发现批量对网络的分类泛化能力存在一定的影响,选择理想的批量和学习率组合,能够获得较好分类错误率,但其影响相对较小,在收敛的情况下,不同批量下的分类错误率相近。
从批量对于网络迭代次数和训练时间的影响角度来看,批量对于网络分类泛化能力的影响较弱,网络的泛化能力和数据集本身性质有较大关系,而批量主要影响网络的迭代次数和训练时间。
4 结论本文基于BP神经网络全批量和单批量学习方法,研究了子批量的神经网络学习方法,并探讨了学习率和批量对于网络收敛性和训练时间的影响,通过实验证明:1)子批量学习方法具有全批量稳定和单批量快速的优点;2)不同的学习率下存在不同的最优批量;3)选择适合的批量,不仅可以大幅缩短网络训练时间,同时还能够取得更好的分类准确率。
| [1] | JACOBS R A. Increased rates of convergence through learning rate adaptation[J]. Neural networks, 1988, 1(4): 295-307. |
| [2] | 刘幺和, 陈睿, 彭伟, 等. 一种BP神经网络学习率的优化设计[J]. 湖北工业大学学报, 2007, 22(3): 1-3. LIU Yaohe, CHEN Rui, PENG Wei. Optimal design for learning rate of BP neutral network[J]. Journal of Hubei university of technology, 2007, 22(3): 1-3. |
| [3] | 贾立山, 谈至明, 王知. 基于随机参数调整的改进反向传播学习算法[J]. 同济大学学报:自然科学版, 2011, 39(5): 751-757. JIA Lishan, TAN Zhiming, WANG Zhi. Modified BP algorithm based on random adjustment of parameters[J]. Journal of Tongji university (natural science), 2011, 39(5): 751-757. |
| [4] | RIEDMILLER M, BRAUN H. RPROP-A fast adaptive learning algorithm[C]//Proceedings of the International Symposium on Computer and Information Sciences (ISCIS VII).Ankara, Turkey, 1992. |
| [5] | CHARALAMBOUS C. Conjugate gradient algorithm for efficient training of artificial neural networks[J]. Devices and systems, IEE proceedings G-Circuits, 1992, 139(3): 301-310. |
| [6] | VOGL T P, MANGIS J K, RIGLER A K, et al. Accelerating the convergence of the back-propagation method[J]. Biological cybernetics, 1988, 59(4/5): 257-263. |
| [7] | DENNIS J E Jr, SCHNABEL R B. Numerical methods for unconstrained optimization and nonlinear equations[M]. Philadelphia, USA: SIAM, 1996. |
| [8] | MOR J J. The Levenberg-Marquardt algorithm: implementation and theory[M]//WATSON G A. Numerical Analysis. Berlin Heidelberg: Springer, 1978: 105-116. |
| [9] | 侯祥林, 陈长征, 虞和济, 等. 神经网络权值和阈值的优化方法[J]. 东北大学学报:自然科学版, 1999, 20(4): 447-450. HOU Xianglin, CHEN Changzheng, YU Heji, et al. Optimum method about weights and thresholds of neural network[J]. Journal of northeastern university: natural science, 1999, 20(4): 447-450. |
| [10] | 刘奕君, 赵强, 郝文利. 基于遗传算法优化BP神经网络的瓦斯浓度预测研究[J]. 矿业安全与环保, 2015, 42(2): 56-60. LIU Yijun, ZHAO Qiang, HAO Wenli. Study of gas concentration prediction based on genetic algorithm and optimizing BP neural network[J]. Mining safety & environmental protection, 2015, 42(2): 56-60. |
| [11] | HAM F M, KOSTANIC I. Principles of neurocomputing for science and engineering[M]. New York, NY: McGraw-Hill Science, 2000. |
| [12] | http://archive.ics.uci.edu/ml/datasets/seeds. |
| [13] | 史峰, 王小川, 郁磊, 等. MATLAB神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社, 2010: 1-3. |



