UAV三维航迹规划区域广,搜素空间巨大,所以要想找到一条最优的飞行轨迹就必定需要占用较长的收敛时间,同时还需要较大的存储空间,这对大部分无人机实际应用来说是不怎么实际的做法。近些年来,国外一些专家对航路规划算法归结出了三类主要的方法:传统算法,如栅格法、Voronoi图法;智能优化算法,如遗传算法、蚁群算法;其他算法,如动态规划算法。传统算法对障碍物要求比较理想化,对实际地形规划出的结果影响很大。动态规划算法,在局部路径上可以达到最优及适用于动态地图,但不能确保全局路径上也可以实现。 智能优化算法[1, 2, 3, 4],如遗传算法,是一种依据生物界的进化规律演化而来的一种方法,它最重要的一个特点是不受函数求导的限制,在隐并行性方面和全局搜索方面有很大优势,在稳定性方面也有显著提高,但算法效率慢,不能适用于动态、真实的地图。
我国在航路规划算法方面也取得了不少的成果,李翊[5]将动态标定遗传算法、自适应遗传算法和大变异遗传算法结合在一起,提出了一种改进的遗传算法,避免了陷入局部最优解与“早熟”;王玥等[6]提出了基于降落伞型搜索域的变步长航迹点搜索和带有威胁信息并归一化后的代价函数,改进了A*算法,提高了搜索效率;韩超[7]提出了一种改进粒子群的航迹规划方法,该方法将UAV的航路规划问题通过目标转换,形成一个考虑威胁优先,路径优化其次的单目标航路优化问题,并引入局部搜索改进粒子群算法求解该问题的收敛性;文献[8]提出了采用蚁群算法解决机器人三维路径规划的问题,通过坐标变换对三维环境进行转换,环境中障碍物抽象成圆形,然后将原点和终点的空间划分成三维立体网格,在原点和终点之间的每一个平面上选定一个点作为航迹节点,从而找到有效的路径,但该方法必须首先进行坐标变换,有误差;胡中华[9]不用进行坐标转换,采用在状态转移策略中引入导引因子和设定最大航迹节点数的方式来实行航迹规划,从而解决标准蚁群算法不易找到目标节点的问题。到目前为止,我国在航路规划技术方面的研究正朝着实用性、实时性、智能化的方向发展。
本文研究四旋翼无人机航迹规划时对上述文献各有借鉴,并将基本蚁群算法做了改进,减少了多余航迹节点,优化了航迹。
1 基于栅格图法的环境模型构建栅格图法[10, 11],是把自由空间C划分成一系列规则的单元格,根据单元格中是否有障碍物和障碍物的覆盖面积来判断。机器人路径规划中栅格图法得到广泛应用[12, 13]。
在对栅格单元划分时有两种方案:一种是只要单元格内有障碍物就判定该单元格是不能通过的;另一种方案是根据单元格内障碍物覆盖面积来判断单元格是否可通过,即单元格内障碍物占的面积如果大于一定比例就认为该单元格是不可通过,否则就认为是可以通过的。第二种方案比第一种方案找到最优解的可能性高,但无人机碰到障碍物的可能性也更高,因此选择第一种方案的更多一些。
在使用栅格图法进行路径搜索时需要考虑的一个重要问题就是分辨率的问题,即每一个单元格的长宽高值。分辨率过高时计算量过大,不符合实际应用;而分辨率过低,规划出的最优解偏离理论最优解过大。
根据自由空间的维数,栅格图法可以分为二维栅格图法和三维栅格图法。二维栅格图是一个平面图形如图 1,三维栅格图是一个三维模魔方形如图 2。二维栅格图中,设X轴最大值为Xmax,最小值为Xmin,X轴划分单位大小为 XGrid,Y轴最大值为Ymax,最小值为Ymin,Y轴划分单位大小为YGrid,则二维栅格图总的网格数目N为
| $$N = {{{X_{\max }} - {X_{\min }}} \over {{X_{Gid}}}} \times {{{Y_{\max }} - {Y_{\min }}} \over {{Y_{Gid}}}}$$ | (1) |
 |
| 图 1 二维栅格图Fig. 1 Two-dimensional raster |
 |
| 图 2 三维栅格图Fig. 2 Three-dimensional raster |
对于三维栅格图,设X轴最大值Xmax,最小值Xmin,X轴划分单位大小为XGrid,Y轴最大值Ymax,最小值 Ymin,Y轴划分单位大小为 YGrid,Z轴最大值Zmax,最小值Zmin,Z轴划分单位大小为ZGrid,则二维栅格图总的网格数目N为
| $$N = {{{X_{\max }} - {X_{\min }}} \over {{X_{Gid}}}} \times {{{Y_{\max }} - {Y_{\min }}} \over {{Y_{Gid}}}} \times {{{Z_{\max }} - {Z_{\min }}} \over {{Z_{Gid}}}}$$ | (2) |
对比式(1)和(2)可以看出二维栅格图和三维栅格图计算量的差别。
本文选用三维栅格图法来划分规划空间。在使用三维栅格图作为环境模型时就必须考虑到三维栅格的分辨率问题,分辨率既不能太大也不能太小。
考虑三维栅格分辨率时,首先要考虑的问题就是四旋翼无人机的体积。要保证四旋翼无人机在飞行过程中能够不碰到障碍物,栅格的长、宽、高要大于四旋翼的长、宽、高,另外还要考虑到误差。本文使用的四旋翼无人机的旋翼轴长55 cm,起落架高约25 cm。另外一方面,设定三维栅格分辨率时还要考虑四旋翼的定位方式。GPS定位是目前最常用的定位方式之一,在四旋翼无人机上安装一个GPS导航模块就可以通过接收GPS信号,进而判断四旋翼无人机的当前位置,所以本文选择使用GPS定位。GPS定位时,纬度上每变化0.001′约为1.837 m,经度上每变化0.001′约为1.281 m,GPS定位时会存在1~2 m的误差。
综上考虑上述两个方面的因素,本文最终选定以纬度值作为横坐标,单位长度为0.002′,约3.674 m;经度值作为纵坐标,单位长度为0.003′,约3.843 m;以地面障碍物的高度作为竖坐标,垂直于海平面,竖坐标单位长度为1 m。这样划分三维栅格单元,就可以兼顾四旋翼的尺寸,又考虑到了GPS定位的误差,从而可以减小碰到障碍物的概率。现以学校部分地图为基础,绘制了基于三维栅格图的三维环境地图。地图所在的位置纬度起始点为45°46.7839′,终止点为45°46.983 9′;经度起始点为126°40.217 2′,终止点为126°40.517 2′;地面水平高度为0。地图大小为(0.002′×100)×(0.003′×100)×(1m×40)。为方便MATLAB作图,纬度和经度上省略度部分上的值,只写分位,也就是说纬度方向上起始点和终止点坐标分别为46.783 9′和46.983 9′,经度方向上起始点和终止点坐标分别为40.2172′和40.5172′。绘制的三维环境的三维图和投影图分别如图 3、4所示。
 |
| 图 3 三维图Fig. 3 Three-dimensional map |
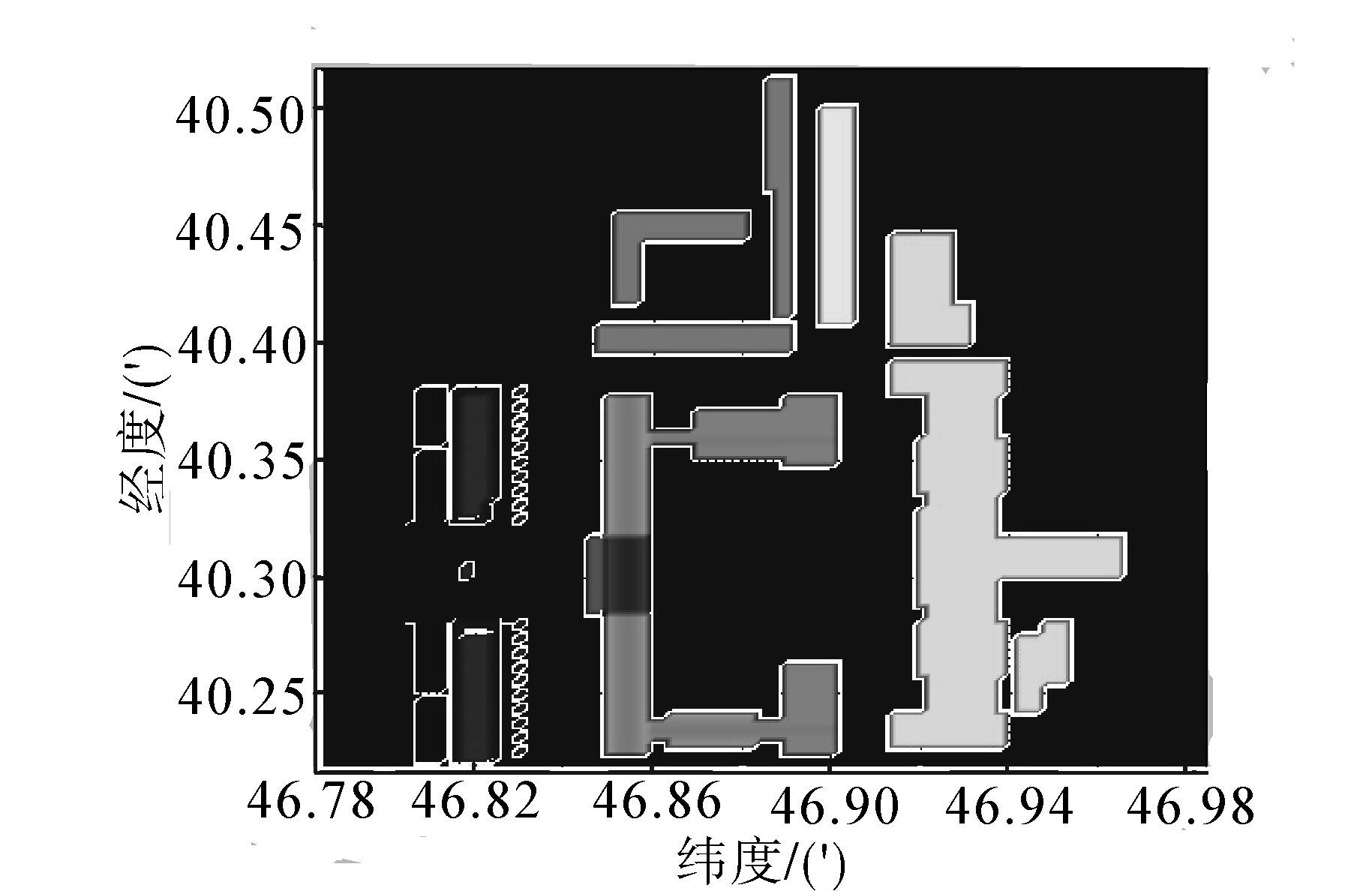 |
| 图 4 投影图Fig. 4 Projection map |
三维蚁群算法解决的问题主要是三维航迹规划问题,该模型和基本的蚁群算法模型有很多不同之处。在原蚁群算法及改进算法的基础之上对其进行了变形,在变形时需要考虑到航迹规划的环境模型。在上文中,已经选定了以纬度值作为横坐标,以经度值作为纵坐标,以高度值作为竖坐标的三维栅格图作为环境模型。因为直接在三维栅格图中对所有的栅格进行搜索找到最优路径需要的计算量和计算时间很大,所以本文采用的方法并不是对所有的栅格进行搜索,而是对部分栅格进行搜索以找到最优航迹。
2.1 算法的数学模型在进行路径搜索时,已知起始点S所在的栅格的坐标值(Xstart,Ystart,Zstart),终止点所在栅格的坐标值(Xend,Yend,Zend),至于栅格单元的大小则是根据上文划分的大小,即XGrid=0.003′,YGrid=0.002′,ZGrid=1 m。航迹规划时需要先选定X方向或Y方向作为四旋翼无人机运行的主方向。选择主方向的方法为:比较起始点和终止点横纵坐标的变化值大小,即比较(Xstart-Xend)/XGrid和(Ystart-Yend)/YGrid的大小,如果(Xstart-Xend)/XGrid大于(Ystart-Yend)/YGrid,则选择X方向作为主方向;否则选择Y方向为主方向。
选定主方向后沿主方向前进方向,例如已经选定X方向为主方向,沿X轴方向从Xstart 到 Xend划分成n=|Xstart-Xend|+1个平面(如图 5所示),编号为Π1,Π2,Π3,…,Πn,那么四旋翼无人机航迹就分成(n-1) 段。假设四旋翼无人机运行至第i个平面 Πi上的一点(Xi,Yi,Zi) 处,那么下一个运行的栅格就在Πi+1上,下一个栅格坐标选择的具体步骤为:X方向上直接以平面Πi+1 的横坐标作为下一个节点的横坐标,即新的X坐标值为Xi+1;Y方向和Z方向坐标值的选择不是直接选择的,而是在平面Πi+1 选择没有障碍物的栅格放入数组Allowedi中;否则被舍弃。然后从中选择一个栅格点作为下一个运行栅格。平面上任意一个栅格(X,Y,Z)作为下一个运行栅格的概率计算为
$$P(X,Y,Z) = \left\{ \matrix{
{{\tau (X,Y,Z) * H(X,Y,Z)} \over {\sum\limits_{}^{} {\tau (X,Y,Z) * H(X,Y,Z)} }} \hfill \cr
(X,Y,Z) \in Allowe{d_i} \hfill \cr
0,(X,Y,Z) \in Allowe{d_i} \hfill \cr} \right.$$
(3)
$$\eqalign{
& H(X,Y,Z) = \cr
& D{(X,Y,Z)^{\omega 1}} \times S{(X,Y,Z)^{\omega 2}} \times Q{(X,Y,Z)^{\omega 3}} \cr} $$
(4)
$$D(X,Y,Z) = \sqrt {{{({X_i} - X)}^2} + {{({Y_i} - Y)}^2} + {{({Z_i} - Z)}^2}} $$
(5)
$$S(X,Y,Z) = \left\{ \matrix{
1,(X,Y,Z)是可达点 \hfill \cr
0,其他 \hfill \cr} \right.$$
(6)
$$\eqalign{
& Q(X,Y,Z) = \cr
& \sqrt {{{({X_i} - {X_{end}})}^2} + {{({Y_i} - {Y_{end}})}^2} + {{({Z_i} - {Z_{end}})}^2}} \cr} $$
(7)
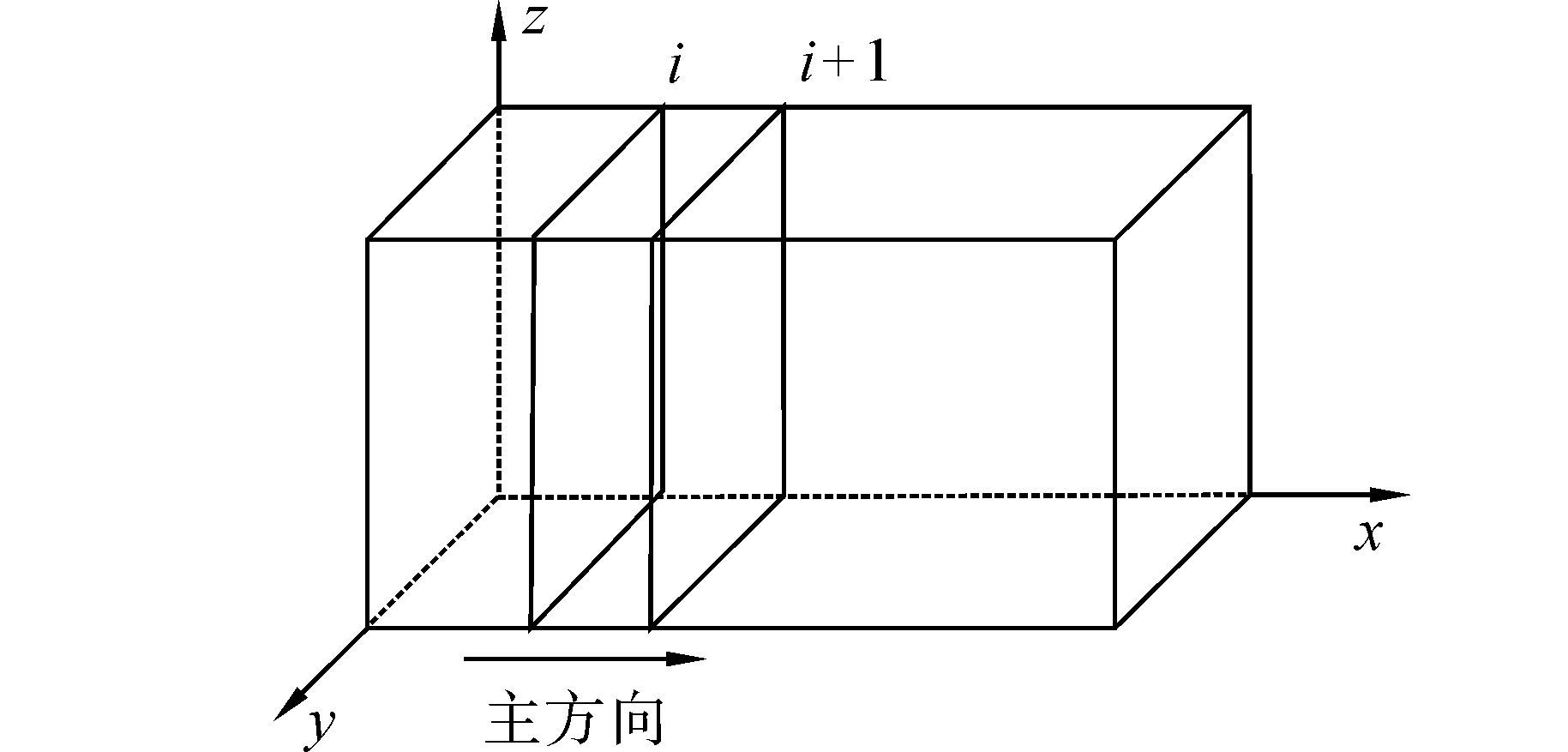 |
| 图 5 主方向选取Fig. 5 Select the main direction |
蚁群算法中蚂蚁是根据信息素浓度来进行搜索路径的,在每走完一段或全部路径时,就要对信息素值进行更新,所以信息素初始值设定和更新对于蚁群算法是否能够成功搜索具有重要影响。本文把信息素值存储在三维空间一系列离散的点中,然后对这些离散点的信息素值进行更新,所以对于每一个栅格来说都有一个信息素值,这个信息素值就代表了该栅格对蚂蚁的吸引程度,每个栅格的信息素值在蚂蚁经过之后都要进行更新。
信息素的更新分为局部更新和全局更新两部分。局部更新是指只要有蚂蚁经过某栅格,该栅格的信息素值就会被更新,更新后栅格的信息素值会被减少,这样这个栅格在以后的搜索中被选中的概率就被降低,而相应地增加其他未被搜索的栅格被搜索的概率,这样就可以达到全局搜素的目的。局部搜索的信息素更新公式为
$${\tau _{x,y,z}} = (1 - \zeta ){\tau _{x,y,z}}$$
(8)
全局信息素更新是指蚂蚁完成一条航迹搜索时,计算该路径的适应度值,从现有的搜索到的路径中选择出最短的航迹,更新适应度值最小的航迹所经过的所有栅格的信息素值,信息素更新公式为
$${\tau _{x,y,z}} = (1 - p){\tau _{x,y,z}} + p\Delta {\tau _{x,y,z}}$$
(9)
$$\Delta {\tau _{x,y,z}} = {K \over {\min (length(m))}}$$
(10)
在充分考虑了评价函数、环境模型和三维蚁群算法模型这些内容之后,下一步需要考虑的就是航迹规划实现的问题。本文中的程序实现主要分为参数初始化设置、航迹搜索和图形绘制3个主要部分,其具体每一步如下所述。
1)参数初始化设置
在进行航迹规划实现时,首先要确定的就是各项参数设置问题。这些参数设置包括起始点的确定、主方向的选取、种群数的确定、迭代次数的选择、航迹搜寻范围选取、信息素初始化设置。
①起始点的确定。当把四旋翼无人机放置在规划空间中的某一点时,放置四旋翼的位置不一定恰好就是栅格图中栅格的位置,这时就需要把该四旋翼无人机所在的栅格的栅格坐标作为航迹规划的起始点。那么,三维栅格地图原点坐标为
$${X_{start}} = ceil({{{S_{lat}} - {X_{Gridstart}}} \over {{X_{Grid}}}}) \times {X_{Grid}} + {X_{Gridstart}}$$
(11)
$${Y_{start}} = ceil({{{S_{lat}} - {Y_{Gridstart}}} \over {{Y_{Grid}}}}) \times {Y_{Grid}} + {Y_{Gridstart}}$$
(12)
$${Z_{start}} = ceil({{{S_{lat}} - {Z_{Gridstart}}} \over {{Z_{Grid}}}}) \times {Z_{Grid}} + {Z_{Gridstart}}$$
(13)
②主方向选取。主方向的选取主要就是以纬度方向为主方向还是以经度方向为主方向的问题。选择两个方向之中栅格变化数最多的方向作为四旋翼无人机航迹规划主方向。主方向选定后还要知道主方向上从起始点到终止点坐标值变化趋势,即坐标值是增加还是减少。如果坐标值增加,那么当从当前平面到下一平面上主方向上坐标值加1个单位值;否则坐标值减1个单位值。假设A方向为主方向,那么从Πi到Πi+1坐标变化为
| $${A_i} + 1 = \left\{ \matrix{ {A_i} + {A_{Grid}},{A_{start}} \le {A_{end}} \hfill \cr {A_i} - {A_{Grid}},其他 \hfill \cr} \right.$$ | (14) |
③种群数选取。
④迭代次数的选择。
⑤航迹搜寻范围选取。如果主方向是A,非主方向的那个纬度或经度方向是B,那么从平面Πi到平面Πi+1,对于B方向上以Yi为中心从Yi-bcmax到Yi+bcmax范围内的点都是可选择作为Yi+1点。同样,对于Z方向上来说以Zi为中心从Zi-hcmax到Zi+hcmax范围内的点都是可选择作为Zi+1点。
⑥信息素初始化。在初始时刻,把三维栅格环境地图中的所有栅格信息素值设置为固定值。
2)航迹搜索
航迹搜索前首先需要确定航迹所选的所有的节点都要在规划空间中,另外在航迹高度上也要有一定的限制。经过观察发现,从地面到距地面2 m范围内障碍物主要是人和车,这些障碍物多是动态的,四旋翼在这个高度范围内飞行容易危害行人和车的正常行动。在距地面2~5 m的范围内主要是较矮的树木,在这个空间中进行飞行时也较容易碰到障碍物,但总的来说还算安全。本文所研究的航迹规划主要是在高于地面2 m的范围内进行的。如果无人机起始点在地面就先让四旋翼飞行距地面一定高度Hmin,飞行过程中也限制四旋翼飞行在这个高度之上。
在航迹搜索过程中,假设PopNum只蚂蚁中的第k只蚂蚁已运行至平面Πi上的点(Xi,Yi,Zi)处,搜索在平面Πi+1上以(Xi+1,Yi,Zi)为中心的count=(2×bcmax+1)×(2×hcmax+1)个点。将count个栅格中所有的可行栅格,即没有障碍物的栅格放入数组Allowedi中。如果数组Allowedi为空,那么将当前点(Xi,Yi,Zi)的Zi坐标值加1,即当前点坐标变为(Xi,Yi,Zi+1),重新搜索平面上的可行栅格,直到数组Allowedi不为空。从数组Allowedi中按照轮盘赌法选出一个可行的栅格作为平面Πi+1上的航迹节点。下一步就是对平面Πi上的节点进行局部信息素更新。
对上述内容重复进行,直到到达平面Πn-1,平面Πi上的节点(Xn-1,Yn-1,Zn-1)直接与平面Πn上的节点(Xend,Yend,Zend)即终止点相连,这样就构成了一条完整的航迹。
按照适应度值函数计算每条航迹的适应度值,比较找出最小适应度值,而最小适应度对应的航迹即为当前最优航迹。
将上述过程迭代N次,这样就找到了迭代N次的最优航迹。
3)图形绘制
利用已经测试到的环境模型的经度、纬度和高度数据绘制三维环境地图,然后在三维环境地图中绘制最优航迹。到此为止,本文就完成了基于蚁群算法的航迹规划与仿真。
2.3 算法的改进 2.3.1 变主方向搜索策略基本三维蚁群算法进行航迹规划时,将Πn-1平面上节点和Πn平面上的节点即终点直接相连容易穿过障碍物。因此首先需要判断两点间的连通性,其具体过程如下。
假设在三维空间存在两点(X1,Y1,Z1)和(X2,Y2,Z2)。两点间的空间直线方程为
$${{X - {X_1}} \over {{X_2} - {X_1}}} = {{Y - {Y_1}} \over {{Y_2} - {Y_1}}} = {{Z - {Z_1}} \over {{Z_2} - {Z_1}}}$$
(15)
$$\left\{ \matrix{
Y = ({Y_2} - {Y_1}) \times (X - {X_1})/({X_2} - {X_1}) + {Y_1} \hfill \cr
Z = ({Z_2} - {Z_1}) \times (Y - {Y_1})/({Y_2} - {Y_1}) + {Z_1} \hfill \cr} \right.$$
(16)
| $$\left\{ \matrix{ X = ({X_2} - {X_1}) \times (Y - {Y_1})/({Y_2} - {Y_1}) + {X_1} \hfill \cr Z = ({Z_2} - {Z_1}) \times (Y - {Y_1})/({Y_2} - {Y_1}) + {Z_1} \hfill \cr} \right.$$ | (17) |
想要知道空间中两点是否连通,首先要判断空间直线经过哪些栅格,然后判断这些栅格所在的经纬度位置的障碍物高度和直线高度关系,如果障碍物高度高于直线高度,那么这条直线经过障碍物,也就是说空间中两点是不可连通的,否则就是可连通的。
对于空间两点,根据两点的X坐标和Y坐标间大小关系,可以分为以下6种关系:
a)X1=X2,Y1和Y2关系任意;
b)Y1=Y2,X1和X2关系任意;
c)X1>X2,Y1>Y2;
d)X1>X2,Y1<Y2;
e)X1<X2,Y1>Y2;
f)X1<X2,Y1<Y2。
图 6,图 7,图 8,图 9,图 10,图 11,绘制了三维空间两点间直线关系在二维平面上的投影的6种情况。分析这6种情况可以发现,当直线与栅格的横向直线相交时,这个交点的上下两个栅格都是直线经过的栅格;当直线与栅格的纵向直线相交时,那么这个交点的左右两个栅格都是直线经过的栅格。所以,当需要判断三维直线投影经过哪些栅格时,只要找出直线与栅格的横纵坐标的交点就可以。
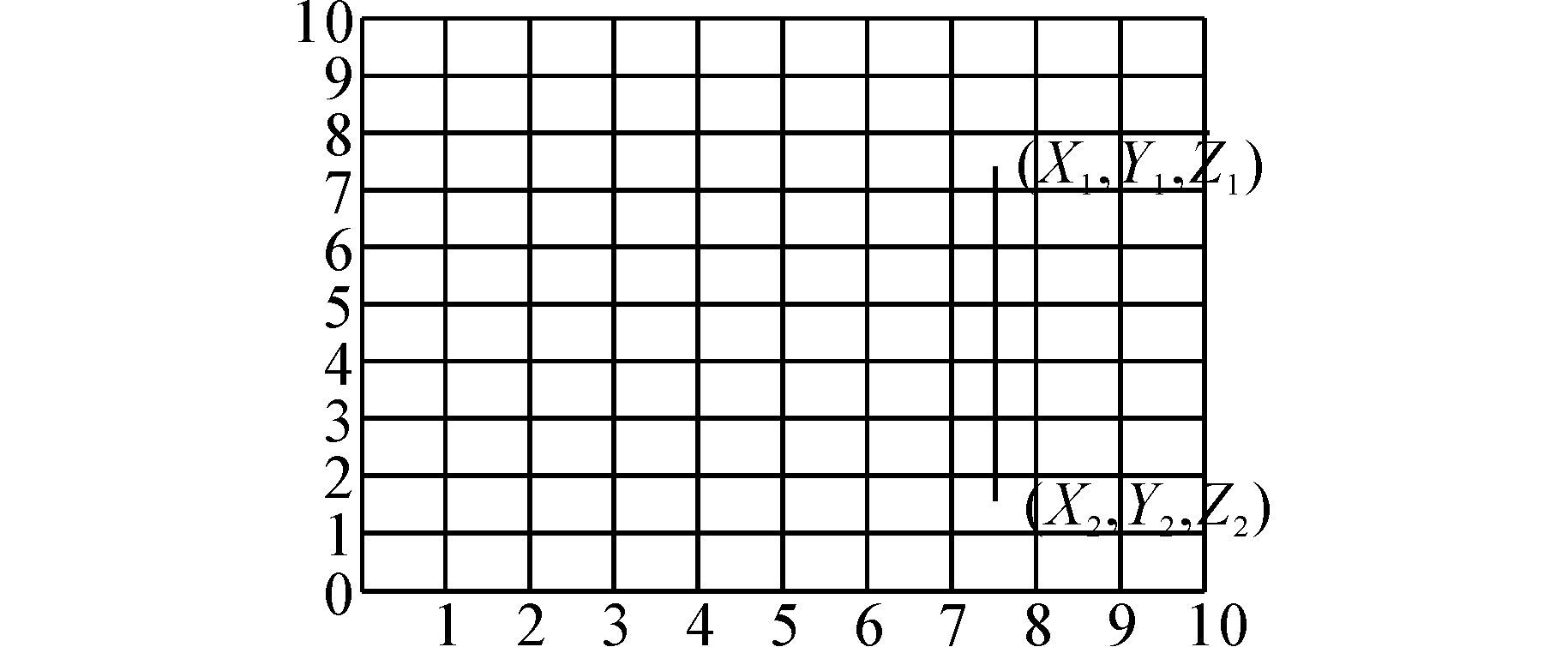 |
| 图 6 X1=X2,Y1和Y2关系任意Fig. 6 X1=X2,Y1 and Y2 arbitrary relationship |
 |
| 图 7 Y1=Y2,X1和X2关系任意Fig. 7 Y1=Y2,X1 and X2 arbitrary relationship |
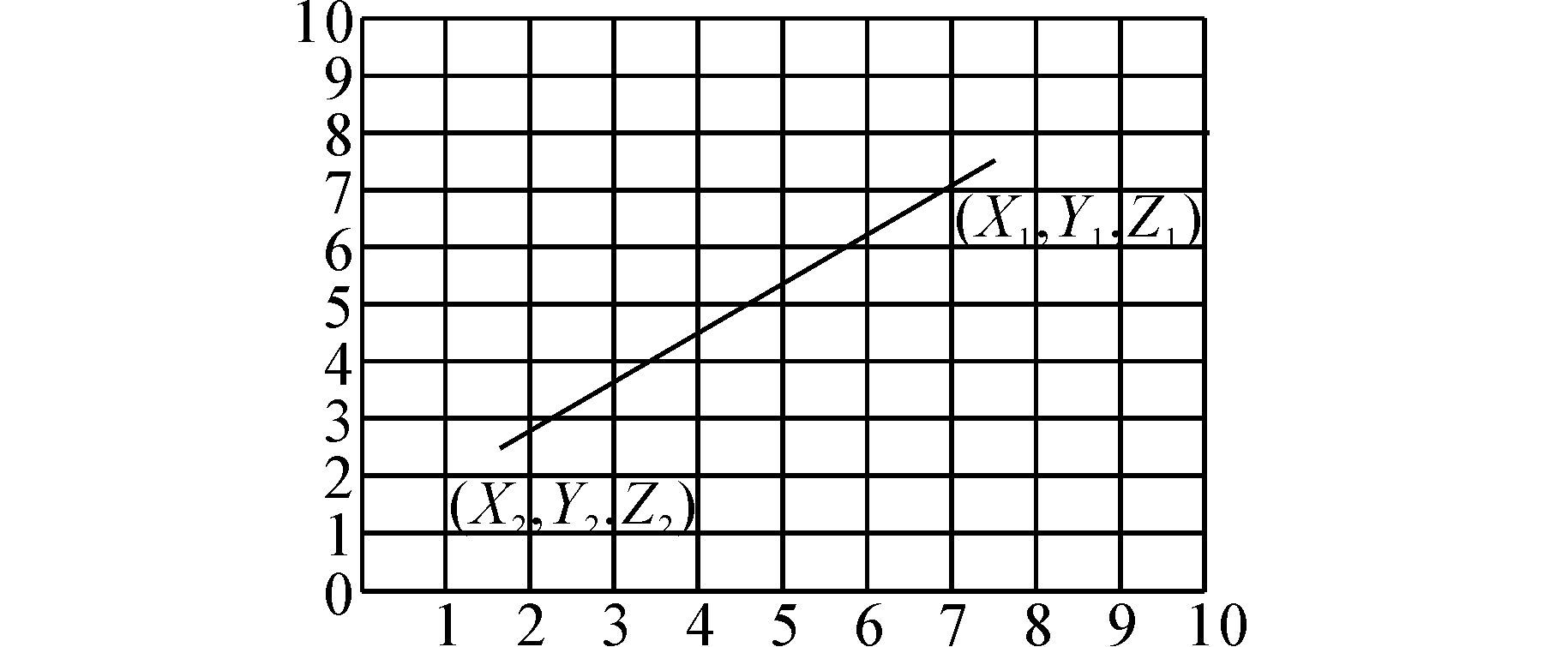 |
| 图 8 X1>X2,Y1>Y2Fig. 8 X1>X2,Y1 >Y2 |
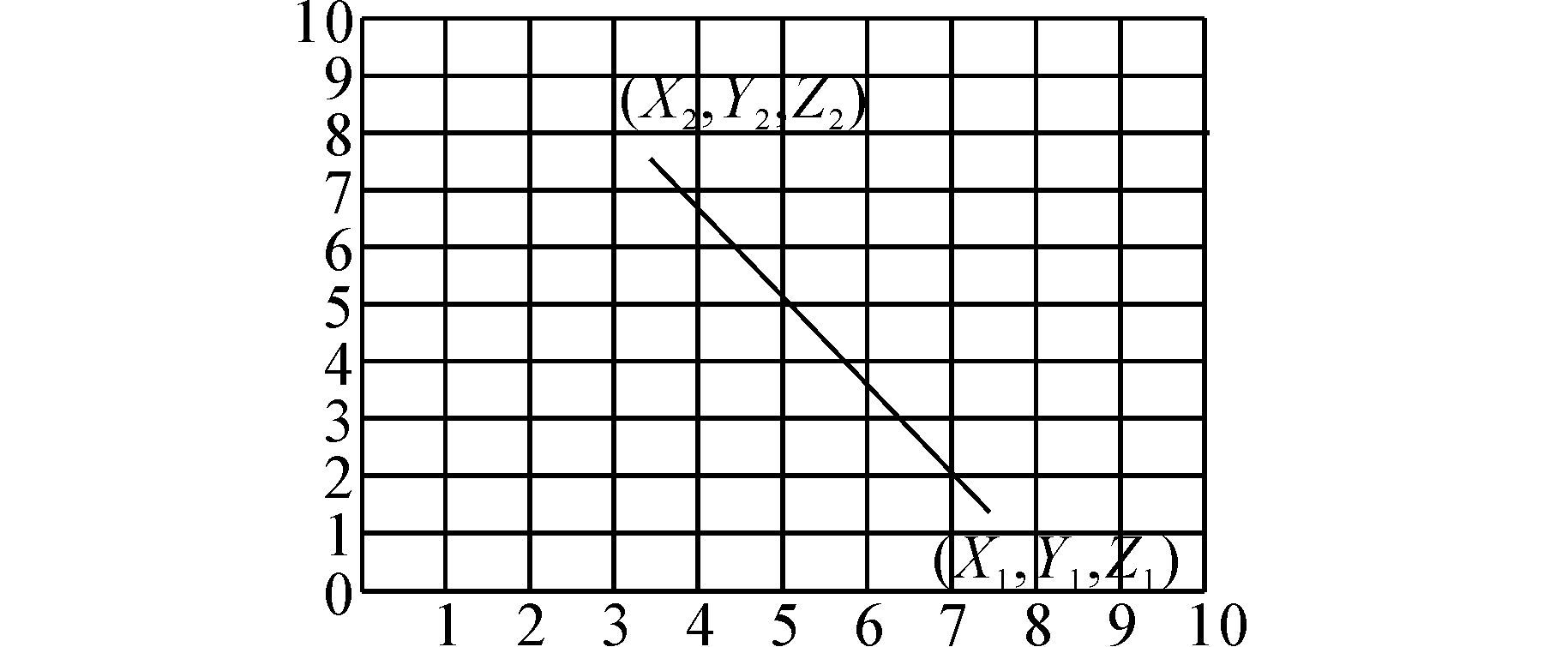 |
| 图 9 X1>X2,Y1<Y2Fig. 9 X1>X2,Y1 <Y2 |
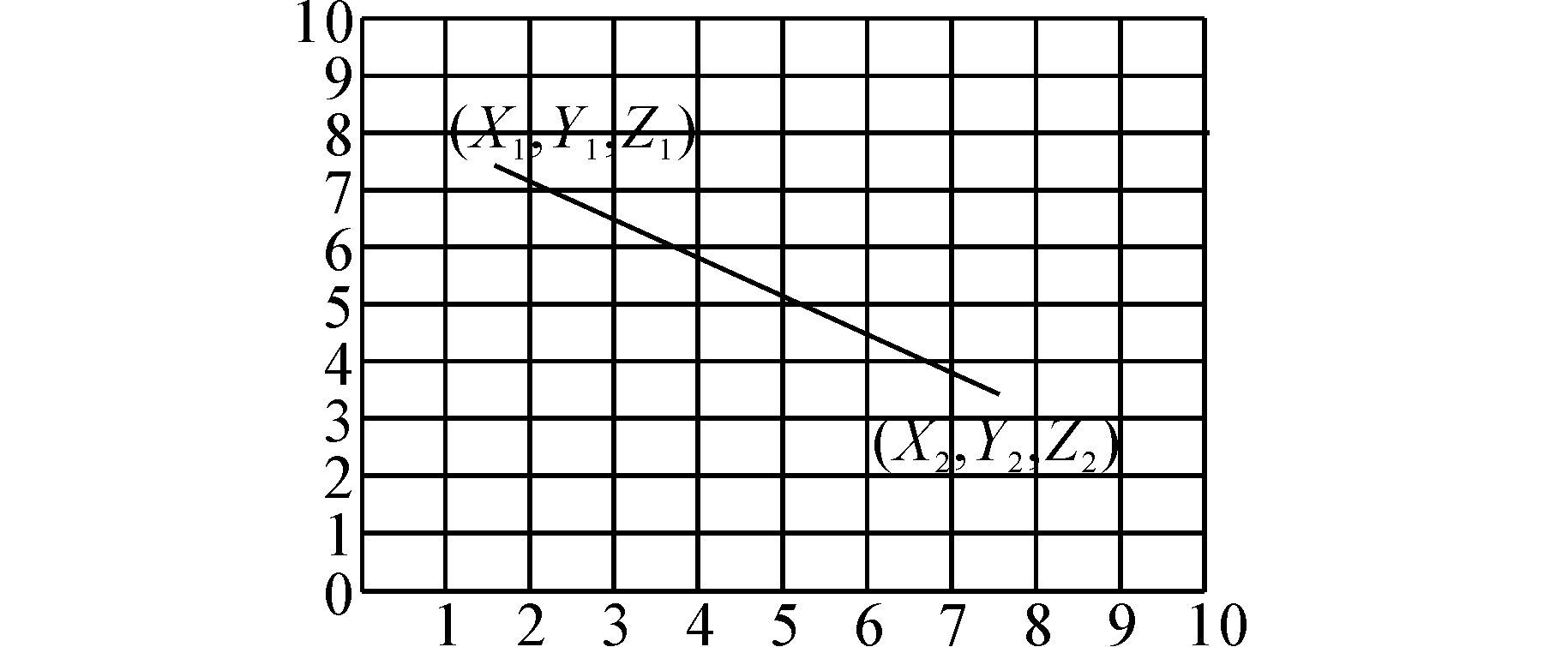 |
| 图 10 X1<X2,Y1>Y2Fig. 10 X1<X2,Y1 >Y2 |
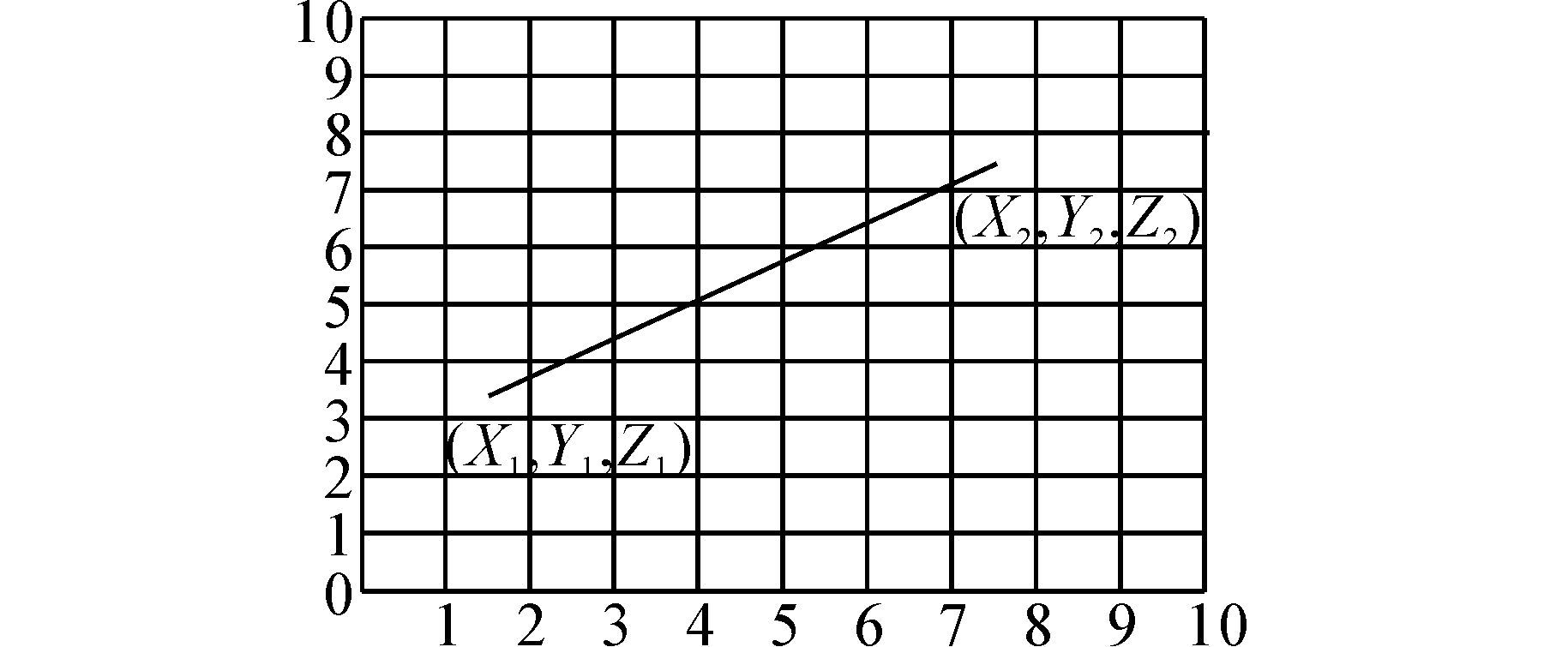 |
| 图 11 X1<X2,Y1<Y2Fig. 11 X1<X2,Y1 <Y2 |
变主方向搜索策略的基本思想是:如果Πn-1平面上的节点和Πn平面上终点是不连通的,那么就以Πn-1平面上的节点(Xn-1,Yn-1,Zn-1)为起始点,以Πn平面上终点(Xend,Yend,Zend)为终止点,再次搜索航迹。记第一次搜索的主方向上平面划分为Π1,1,Π1,2,…,Π1,n1,搜索节点依次为(X1,1,Y1,1,Z1,1),(X1,2,Y1,2,Z1,2),…,(X1,n1-1,Y1,n1-1,Z1,n1-1);同理,第m次搜索的主方向上平面划分为Πm,1,Πm,2,…,Πm,nm,搜索节点依次为(Xm,1,Ym,1,Zm,1),(Xm,2,Ym,2,Zm,2),…,(Xm,n1-1,Ym,n1-1,Zm,n1-1)。最终的三维航迹为(X1,1,Y1,1,Z1,1),…,(X1,n1-1,Y1,n1-1,Z1,n1-1),(X2,2,Y2,2,Z2,2),…,(X2,n1-1,Y2,n1-1,Z2,n1-1),…,(Xm,2,Ym,2,Zm,2),…,(Xm,nm-1,Ym,nm-1,Zm,nm-1),(Xend,Yend,Zend)。
2.3.2 简化航迹策略航迹节点过多意味着四旋翼无人机在飞行的过程中需要转折次数过多,采用一定的简化策略来减少航迹节点既能减小适应度值还能减小航迹主要思路是:假设变主方向搜素策略所搜索出的一条可行航迹为route=(r1,r2,…,rn)。首先把节点r1放入新航迹数组newroute中,判断r1与rn的连通性,如果是连通的,把r1放入数组newroute中;否则判断r1与rn-1的连通性,直到找到一个点ri与r1是连通的。对ri进行相同的操作,直到终止点。
3 三维粒子群算法 3.1 粒子群算法的主要流程粒子群算法进行航迹搜索时分以下几个步骤:
1)确定起始点和终止点,对粒子群种群数、迭代次数等参数进行设定;
2)搜索num条可行航路,根据适应度函数计算个航路的适应度值,选取适应度值最小的航路R,根据主方向选取的不同将航路分成d段;
3)根据主方向的不同对速度进行分段初始化,由初始速度和航路R找出PopNum条航路作为各个粒子的初始航路;
4)根据粒子群初始航路计算各粒子的局部最优航路,再比较粒子群的局部最优航路找出适应度值最小的航路作为全局最优航路;
5)迭代开始,迭代次数k=0;
6)粒子群i=0;
7)根据迭代次数计算每一代ω的值,根据当前全局最优航路和局部最优航路对粒子群速度进行分段更新,更新完速度之后再对粒子群中各粒子的位置进行更新;
8)计算粒子i的新的航路的适应度值与粒子的局部最优值进行比较,如果当前航路的适应度值小于粒子i的最优航路的适应度值,以当前航路替换最优航路成为粒子i的新的最优航路;
9)如果i<PopNum,i值加1,重复7),否则执行10);
10)更新完所有粒子的位置后比较全局最优航路适应度值和粒子群当前局部最优航路适应度值,如果有某粒子的局部最优航路的适应度值小于全局最优航路的适应度值就用该粒子的航路代替全局最优航路成为新的全局最优航路;
11)如果k<N,k值加1,重复6),否则转12);
12)绘制三维地图和三维航迹。
粒子群算法被用来解决四旋翼无人机航迹规划问题,会存在适应度值过大的问题。即使增加种群数量和迭代次数也不能很好解决这个问题,文中提出简化航迹的策略来减少航迹节点,降低适应度值。
简化策略的具体实行步骤与前文中的蚁群算法航迹简化策略相似,也是先判断终点和当前点的连通性,如果是可连通的则简化结束,否则判断和倒数第二个节点的连通性,如此反复,直到简化完成。在粒子群算法中,每次计算适应度值时不是直接计算,而是先将航迹简化,比较各航迹简化后的适应度值,最后保留适应度值最小的航路,该最小航路的简化航路就是最终的航迹,直接在三维环境中绘制即可。
4 仿真与分析 4.1 三维蚁群算法仿真分析实验时,设定纬度起始点为45°46.963 9′,终止点为45°46.803 9′;经度起始点为126°40.502 2′,终止点为126°40.247 2′;地面水平高度为0.25 m。即(46.963 9,40.502 2,0.25)为起点,(46.803 9,40.247 2,0.25)为终点。图 12、13分别是用基本三维蚁群算法搜索到的三维航迹图形和三维航迹在二维平面上的投影。图 14、15分别是采用了变主方向策略改进后的算法搜索得到的三维航迹图形和三维航迹在二维平面上的投影。
 |
| 图 12 蚁群算法搜索到的三维航迹图形Fig. 12 Three-dimensional graphics searched by ant colony algorithm |
 |
| 图 13 三维航迹在二维平面上的投影Fig. 13 Three-dimensional trajectory projected on |
从图 12、13中可以看出,基本蚁群算法搜索到的航迹出现了穿过障碍物的现象,这显然是不允许的。改进后的航迹节点数为173个,航迹长度为808.040 2 m,如果四旋翼以1~2 m/s的速度飞行时,可以飞行6.733 6~13.467 3′。从图 14、15可以看出,改进后的算法满足航迹规划的需要,且能够有效避免航迹穿过障碍物的现象出现。
 |
| 图 14 加入变主方向策略后的三维航迹图Fig. 14 Three-dimensional graphics including the strategy of converting the main direction |
 |
| 图 15 加入变主方向策略的航迹二维投影图Fig. 15 The two-dimensional projection of track including the strategy of converting the main direction |
选定起点坐标为(46.9639,40.5022,0.25),终点坐标为(46.8039,40.2472,0.25),种群数PopNum=25,迭代次数 N=50,其他参数都相等的情况下,对简化策略使用前和使用后进行对比。
图 16、17分别使用简化策略前的三维航迹及三维航迹在二维平面上的投影,航迹经过173个航迹节点,航迹长度为812.070 6 m。图 18、19是使用简化策略后的三维航迹及三维航迹在二维平面上的投影,航迹中经过5个航迹节点,航迹节点长度为522.765 8 m。可以看出,简化后的航迹比简化前的航迹,在有效避开障碍物的同时极好地改善了三维航迹的形状,航迹长度大大缩短,更符合实际的需要。
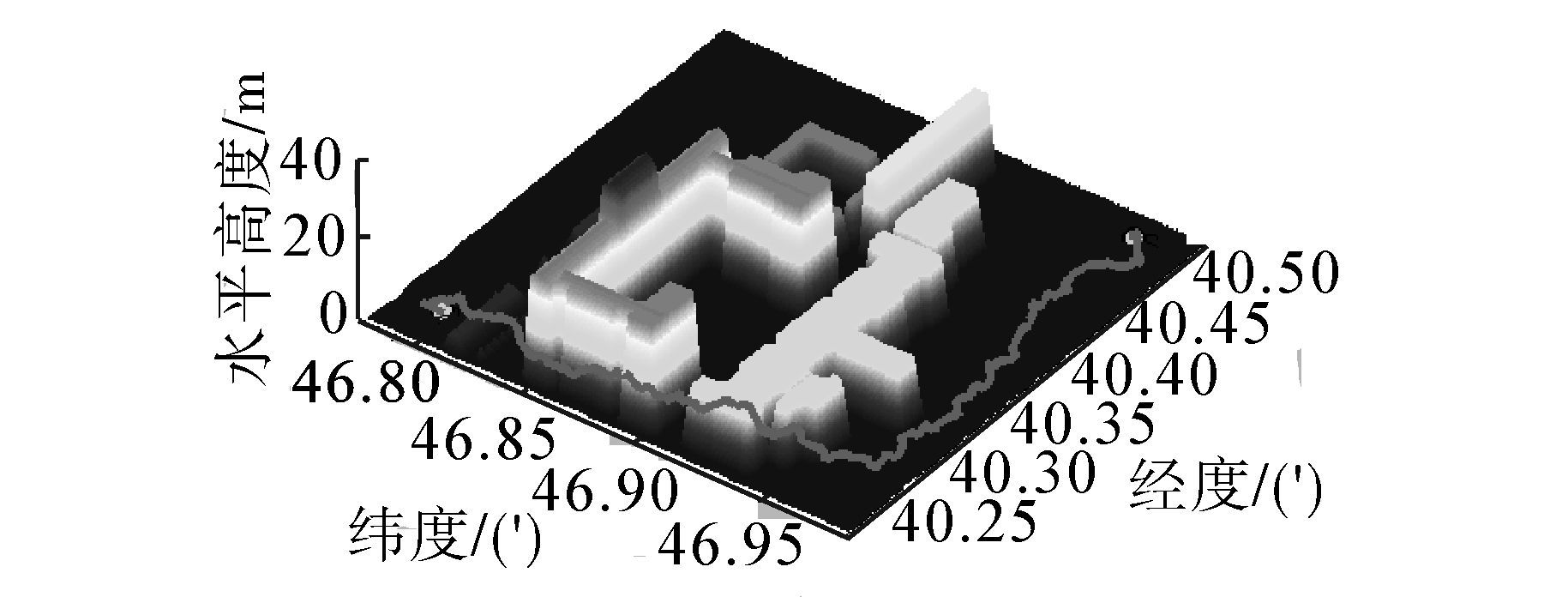 |
| 图 16 未使用简化策略的三维航迹图Fig. 16 Three-dimensional graphics without simplification strategy |
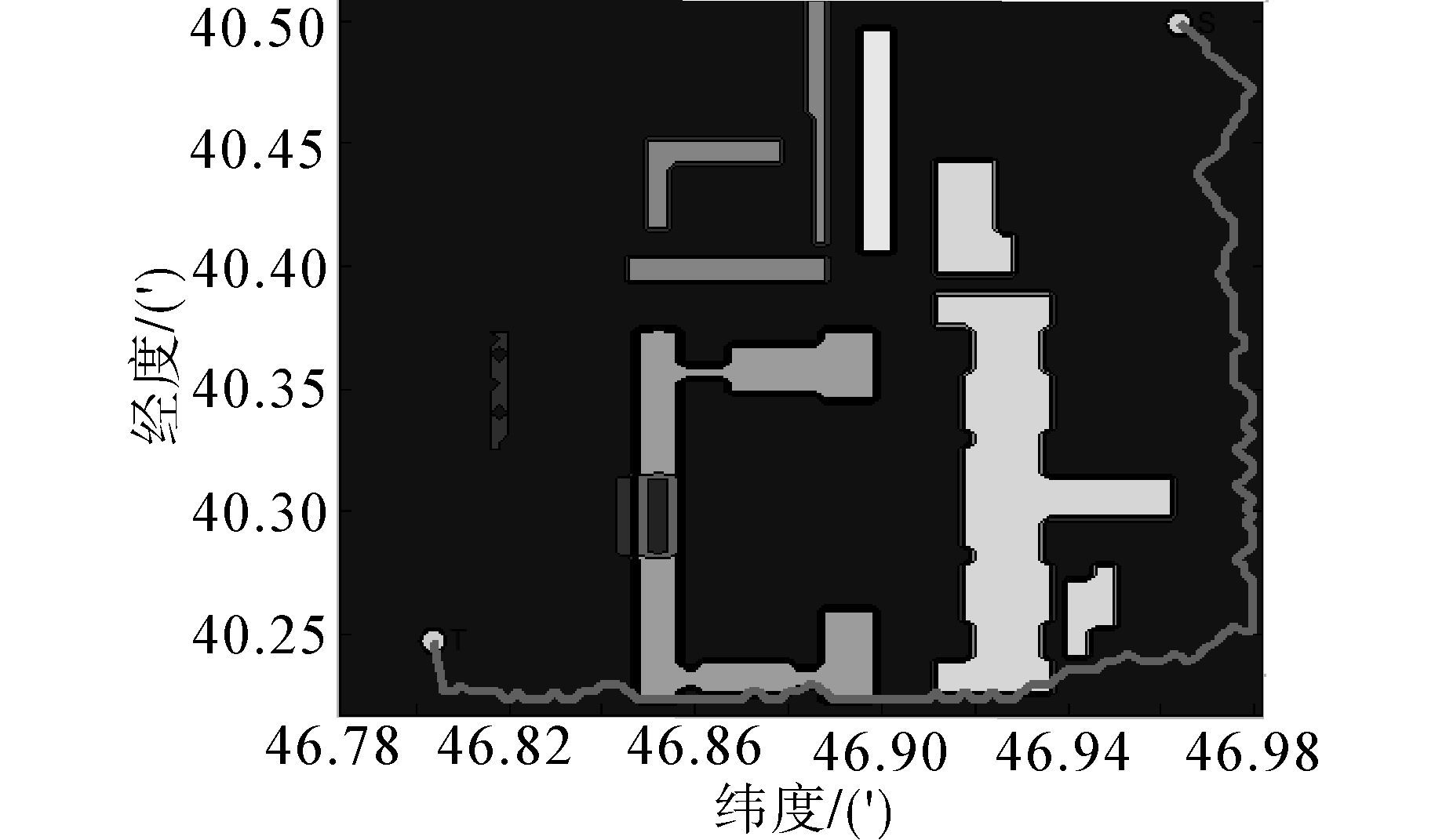 |
| 图 17 未使用简化策略的航迹二维投影图Fig. 17 The two-dimensional projection of track without simplification strategy |
 |
| 图 18 使用简化策略的三维航迹图Fig. 18 Three-dimensional graphics with simplification strategy |
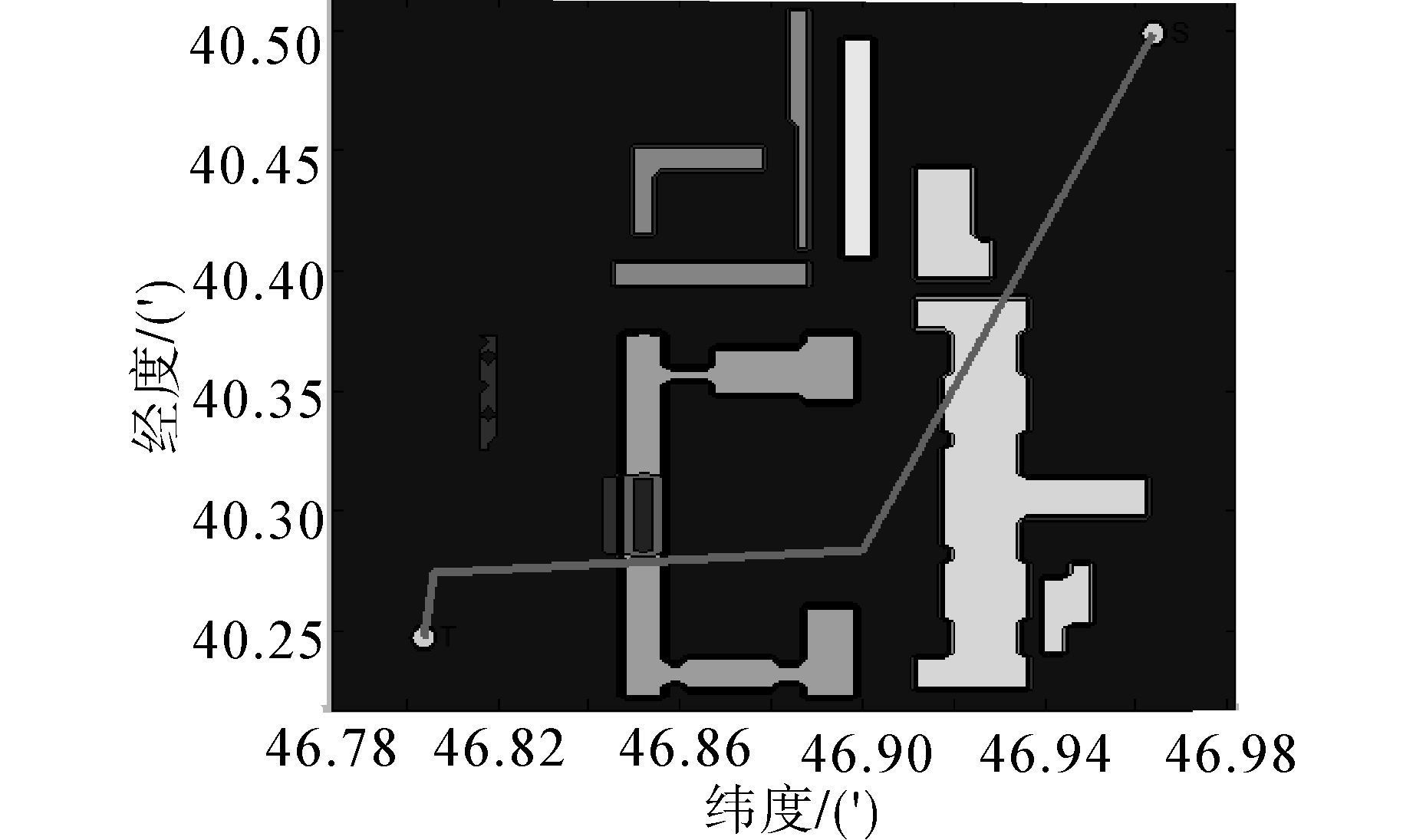 |
| 图 19 使用简化策略的航迹二维投影图Fig. 19 The two-dimensional projection of track with simplification strategy |
为了进一步评价简化策略实施对航迹搜索结果的影响,图 20、21分别是简化策略实施前后适应度值统计图和搜索时间统计图。
 |
| 图 20 简化前后适应度值统计Fig. 20 Statistics of fitness value with and without simplification |
 |
| 图 21 简化前后搜索时间统计Fig. 21 Statistics of searching time with and without simplification |
从图中可以看出,简化策略实施前后花费差不多的时间,与简化策略实施前相比,简化策略实施后适应度值大大减小,从而进一步证明了简化策略实施的有效性。
4.2 三维蚁群算法与三维粒子群算法对比基于粒子群算法的航迹规划所使用的评价函数和环境模型与蚁群算法中所使用的评价函数和环境模型相同。但用传统粒子群算法实现航迹规划,也存在航迹节点过多的问题,所以同样采用了上文提出的简化策略。将加入简化策略后的粒子群算法与改进后的蚁群算法相比较。
设定蚁群算法和粒子群算法主要参数为:
蚁群算法:种群数取值25,高度系数取值1,信息素挥发系数取0.5;粒子群算法:初始时选定可行航迹条数取值50,种群数量取值20,高度系数取值1,学习因子取2。
起点坐标均为(46.9349,40.4407,0.25),终点坐标均为(46.8809,40.3387,0.25)。运行20次。得到蚁群算法和粒子群算法的最优航迹如图 22、23。
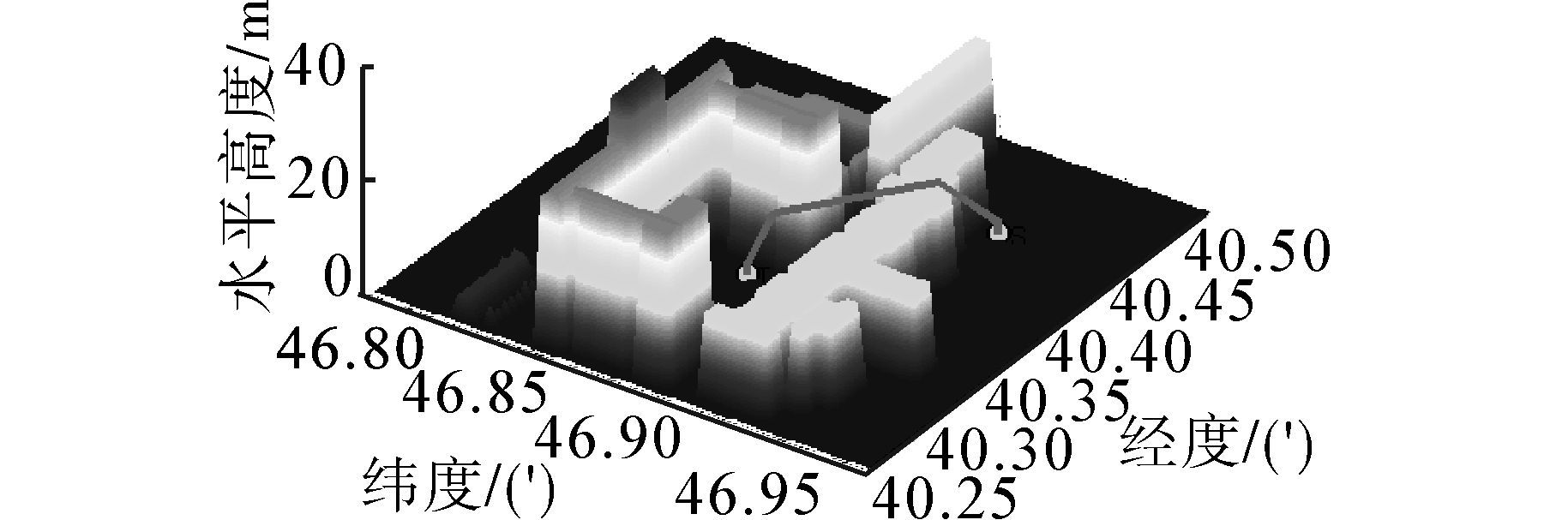 |
| 图 22 蚁群算法搜索到的最优三维航迹图形Fig. 22 The best three-dimensional graphic searched by Ant colony algorithm |
 |
| 图 23 粒子群算法搜索到的最优三维航迹图形Fig. 23 The best three-dimensional graphic searched by Particle swarm optimization |
为了评价一个算法的优劣,需要用一些指标来评价,常用的算法指标包括:时间复杂度、空间复杂度、正确性、可读性、健壮性。
结合本文所研究课题内容,重点引入了稳定性[14]、误差率、航迹规划搜索时间这3个指标[15]进行对比。
航迹规划时已经有S1,S2,…,Sm共m个样本个体的样本,样本最大值Smax,最小值Smin,那么样本绝对误差可以表示为
| $${S_{ae}} = ({S_{\max }} - {S_{min}})/2$$ | (18) |
样本的均值描述了样本的平均情况,表示为
| $$S = \sum\limits_{i = 1}^m {{S_i}/m} $$ | (19) |
样本标准差反映了样本的离散程度,表示为
| $$\sigma = \sqrt {{{\sum\limits_{i = 1}^m {{{({S_i} - {S_{mean}})}^2}} } \over m}} $$ | (20) |
统计蚁群算法和粒子群算法航迹规划适应度值如表 1所示。从表中可以看出,蚁群算法搜索出的航迹的适应度值更为稳定一些。
| 算法 | 最小值 | 最大值 | 均值 | 中值 | 标准差 |
| ACO | 225.958 | 238.094 | 232.224 | 232.658 | 2.665 |
| PSO | 218.996 | 284.540 | 248.474 | 239.351 | 22.283 |
误差率描述了样本平均值与理论值的偏差程度,反映了算法对问题的优化程度,误差率越小则表示算法的优化性能越好,也就是找到的最优值越接近理论最优值。误差率计算公式为
$$e = {{{S_{mean}} - S * } \over {S * }} \times 100\% $$
(21)
本文的航迹规划过程中,环境相同时,以粒子群算法和蚁群算法规划处的航迹适应度值最小值作为理论最优值,以每种算法各自的平均值来计算两种算法各自的误差率。两种算法的误差率如表 2。
| 算法 | 理论最优值 | 均值 | 误差率/% |
| ACO | 218.966 | 232.223 | 6.055 |
| PSO | 218.966 | 248.474 | 13.476 |
航迹规划搜索时间是指从算法开始到找到最优航迹经历的时间。一般来说,规划时间越少算法优化性能越好。表 3是蚁群算法和粒子群算法分别进行航迹搜索时的搜索时间,从表中可以看出,粒子群算法进行航迹搜索时的搜索时间比蚁群算法的小得多,同时,蚁群算法的规划时间更稳定一些,也间接说明蚁群算法搜索稳定性更高一些。
| 算法 | 最小值 | 最大值 | 均值 | 中值 | 标准差 |
| ACO | 20.091 | 20.831 | 20.457 | 20.440 | 0.141 |
| PSO | 0.026 | 0.578 | 0.228 | 0.171 | 0.162 |
从标准差、误差率、规划时间3个方面对两种算法进行对比和评估,从对比和评估的结果看来,蚁群算法稳定性更高一些,而粒子群算法航迹规划时间更少一些。
5 结束语本文详细介绍了四旋翼无人机航迹规划的三维环境模型构建并结合蚁群算法在航迹搜索中出现的问题对算法提出了改进,仿真实验证实改进后的算法减小了适应度值,使航迹得到了优化。但是根据搜索时间的统计图可以得出搜索时间较改进前长。本文还与同样改进策略的粒子群算法作比较,得出蚁群算法稳定性更高,但是规划时间有点长。因此,在后续的工作研究中要结合实际飞行测试实验并将蚁群算法与更多智能算法做横向对比,进而优化参数以便提高算法的规划时间。
| [1] | METEA M, TSAI J. Route planning for intelligent autonomous land vehicles using hierarchical terrain representation[C]//Proceedings of IEEE International Conference on Robotics and Automation. Raleigh, NC, USA, 2010: 1947-1952. |
| [2] | 谢奉军, 张丹平, 黄蕾,等. 旋翼无人机专利申请现状与技术发展趋势分析[C]//第六届中国航空学会青年科技论坛文集. 沈阳, 2014. |
| [3] | LIU Hongyun, JIANG Xiao, JU Hehua. Multi-goal path planning algorithm for mobile robots in grid space[C]//Proceedings of the 25th Chinese Control and Decision Conference. Guiyang, 2013: 2872-2876. |
| [4] | GALCERAN E, CARRERAS M. A survey on coverage path planning for robotics[J]. Robotics and Autonomous Systems, 2013, 61(12): 1258-1276. |
| [5] | 李翊, 王朕, 姜鹏, 等. 四旋翼无人飞行器的航迹规划[J]. 舰船电子工程, 2014, 34(12): 58-61.LI Yi, WANG Zhen, JIANG Peng, et al. Path planning of quad-rotor[J]. Ship electronic engineering, 2013, 61(12): 1258-1276. |
| [6] | 王玥, 张志强, 曹晓文. A*改进算法及其在航迹规划中的应用[J]. 信息系统工程, 2014 (1): 89-91. |
| [7] | 韩超, 王赢. 一种基于改进PSO的无人机航路规划方法[J]. 舰船电子工程, 2014, 34(4): 49-53. HAN Chao, WANG Ying. Path planning of UAV based on an improved PSO algorithm[J]. Ship electronic engineering, 2014, 34(4): 49-53. |
| [8] | 胡小兵, 黄席樾. 基于蚁群算法的三维空间机器人的路径规划[J]. 重庆大学学报, 2004, 27(8): 132-135.HU Xiaobing, HUANG Xiyue. Path planning in 3-D space for robot based on ant colony algorithm[J]. Journal of Chongqing university: natural science edition, 2004, 27(8): 132-135. |
| [9] | 胡中华. 基于智能优化算法的无人机航迹规划若干关键技术研究[D]. 南京: 南京航空航天大学, 2011: 46-52. |
| [10] | KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. International Journal of Robotics Research, 1986, 5(1): 90-99. |
| [11] | BAIRD C, ABRARNSON M. A comparison of several digital map-aided navigation technique[C]//The Proceedings of IEEE PLANS. Halifax, Nova Scotia, Canada, 1984: 286-293. |
| [12] | 任世军, 洪炳熔, 黄德海. 一种基于栅格扩展的机器人路径规划方法[J]. 哈尔滨工业大学学报, 2001, 33(1): 68-72.REN Shijun,HONG Bingrong, HUANG Dehai. A robot path planning algorithm based on grid expansion[J]. Journal of Harbin institute of technology, 2001, 33(1): 68-72. |
| [13] | 吕太之, 赵春霞. 基于改进概率栅格分解的路径规划算法[J]. 计算机工程, 2007, 33(21): 160-162, 165.LV Taizhi,ZHAO Chunxia. Path planning based on improved probabilistic cell decomposition[J]. Computer engineering, 2007, 33(21): 160-162, 165. |
| [14] | 王凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2001. |
| [15] | WEISS M A. 数据结构与算法分析[M]. 冯舜玺, 译. 2版. 北京: 机械工业出版社, 2004. |



