2. 重庆邮电大学 自动化学院, 重庆 400065;
3. 重庆邮电大学 光电工程学院, 重庆 400065
2. College of Automation, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;
3. College of Opto Electronic Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
为了提高语音识别系统的鲁棒性,谱减法、卡尔曼滤波[1, 2]和麦克风阵列[3]等语音增强技术得到应用和推广。语音特征的失真造成声学空间的变形,对此声学模型可以相应地调整,以弥补训练和测试语音之间的差异,这种调整通常被称为噪声模型补偿技术[4, 5]。由于语音去噪的复杂性,甚至小词汇的自动语音识别系统都采用了相对复杂的处理方法[6]。这些复杂的处理方法往往会造成较大的计算量和不必要的时延,降低自动语音识别系统的灵活性[7]。
因此本文综合考虑自动语音识别系统的鲁棒性和灵敏性,有针对性地提出了一种简洁的语音信号后处理方法——MVDA后处理法。同时,也改善了传统的MFCC特征提取方法中采用三角滤波器组带来的相邻频带之间的频谱能量相互泄露,且不利于反映共振特性的问题,为整个语音识别系统的优化提供了基础。实验表明,MVDA后处理法在不同的噪声环境中的鲁棒性和灵敏性都要高于传统的MFCC特征提取法。
1 噪声分类和MFCC自动语音识别系统的鲁棒性取决于噪声、语音特征和语音信号处理方法。本节首先定义了日常声学环境中常见的噪声类型,对噪声的分类有利于本文更加清晰地分析特征失真,并且有利于描述MVDA后处理法。
1.1 噪声的分类通常处理的噪声分为加性噪声和卷积噪声。加性噪声可以描述为
$$x(t) = s(t) + n(t)$$
(1)
$$x(t) = s(t) * n(t)$$
(2)
$$x(t) = s(t) * h(t) + n(t)$$
(3)
式(3)可以被看成是一般噪声情况下,表明语音成分与噪声成分的一种方法,可以简化为
$$x(t) = F(s(t))$$
(4)
另一种失真产生于噪声环境下样本采集过程中的Lombard效应[8],如延长元音的持续时间和频谱向高频率倾斜,从而改变了语音信号本身。因此,噪声环境下的{s(t)}本身存在失真,这种失真可以看做是式(4)的一个特例。
1.2 基础语音特征MFCC本文以Mel频率倒谱系数为基础,提出了新的语音特征提取法。MFCC的分析基于人的听觉机理,即根据人的听觉实验结果来分析语音的频谱,期望获得更好的语音特性。MFCC分析依据的听觉机理有两个:1)人的主观感知频域的划定并不是线性的;2)人耳听觉的临界带原理。
一帧语音信号的MFCC参数可以表示为$C \buildrel \Delta \over = {(C[I] \cdot \cdot \cdot Q[J])^T}$,这里D表示倒谱系数的维数。MFCC的定义如下:
$$C = GInQ$$
(5)
| $$\eqalign{ & {G_{ij}} = \sqrt {{2 \over J}} COS\left( {{{\pi i} \over J}(j - 0.5} \right) \cr & i = 1,2, \cdot \cdot \cdot ,I,j = 1,2, \cdot \cdot \cdot ,J \cr} $$ | (6) |
MFCC特征提取方法采用三角滤波器组处理,同时也带来的相邻频带之间频谱能量的相互泄露。
2 MVDA后处理法步骤MVDA后处理法在MFCC特征提取法的基础上,融合了均值消减、方差归一化、时间序列滤波和加权自回归移动平均滤波法,图 1为MVDA后处理法基本步骤。
 |
| 图 1 MVDA后处理法Fig. 1 Postprocessing of MVDA |
MVDA的提出是为了解决MFCC特征参数的加性和卷积噪声的问题,均值消减和方差归一化在语音处理中已经得到了相对广泛的应用[9, 10, 11, 12]。本文提出了结合时间序列滤波和加权自回归移动平均滤波法在频域的应用,可以获得相较于单独使用均值消减和方差归一化更好的效果。
本文用C(τ)表示第τ帧语音的特征,则均值消减表示为
$${\bar C^{(\tau )}} = {G^{(\tau )}} - \mu $$
(7)
$${\hat C^{(\tau )}}[d] = ({\sigma ^2}[d]) - 1/2{\bar C^{(\tau )}}[d]$$
(8)
$${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over
C} ^{(\tau )}} = {{\sum\limits_{k = 1}^w {{k^2}\hat C(\tau + k)} - \sum\limits_{k = 1}^w {{{(k - 1)}^2}{{\hat C}^{(\tau - k)}}} } \over {(4k - 2)\sum\limits_{k = 1}^w {{k^2}} }}$$
(9)
$$\eqalign{
& {{\tilde C}^{(\tau )}} = [{{\tilde C}^{(\tau - m)}} + \cdot \cdot \cdot + (m - 1){{\tilde C}^{(\tau - 1)}} + m{{\tilde C}^{(\tau )}}]/{m^2} + \cr
& [(m - 1){{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over
C} }^{(\tau - 1)}} + \cdot \cdot \cdot + {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over
C} }^{(\tau + m)}}]/{m^2} \cr} $$
(10)
均值μ和方差σ2的估计可以采用多种方法。在方差估计法[13]中,均值和方差根据一整段对话语音估计。如果环境是静态的,则这种估计是相对稳定的。而根据在线估计法[14],均值和方差可以不依赖将来的特征观察值,根据当前样本估计,这种策略时延低,适用于灵敏度要求高的系统。介于这两种策略之间的是语句估计法。本文中的所有结果都基于语句估计,其定义为 $$\eqalign{ & \mu = {1 \over T}\sum\limits_{\tau = 1}^T {{C^{(\tau )}}} \cr & {\sigma ^2} = [d] = {1 \over T}\sum\limits_{\tau = 1}^T {({C^{(\tau )}}[d]} - \mu [d]{)^2} \cr} $$ 式中:T为给定语句中的帧数。注意在语句归一化法中,结果可能被语音前后的空白和噪声影响[15],本文的研究假设在计算均值和方差统计之前,已经对语音进行了合理的分割。
3 噪声影响与MVDA滤波法分析关于频域加性和卷积噪声,本文均作了详细的分析。本节从理论上推导MVDA滤波法,分析均值消减、方差归一化、时间序列滤波和加权自回归移动平均滤波法的去噪效果,并分析在滤波前后噪声对语音特征的影响。
3.1 均值消减本文首先分析卷积噪声对语音特征造成的失真,并且得出均值消减可以有效去除卷积噪声。分析表明,频域均值消减导致参数在时不变卷积噪声下是稳定的。
卷积噪声在频域内表现为乘法运算,因此{s(t)}、{s(t)}和{h(t)}的功率谱可以表示为 $${P_x}[k] = {P_s}[k]{P_h}[k]$$ 式中:Px[k]=|X[k]2|,X[k]为语音信号x[n]的离散傅里叶变换。根据式(5),x的第i维参数为 $${C_x}[i] = \sum\limits_{J = 1}^J {{G_{ij}}} In(\sum\limits_{k = 0}^{N - 1} {{F_{jk}}{P_x}[k]} )$$ 式中:Fjk表示第j个Mel特征滤波器的第k条谱线。
一般情况下,Cx和Cs并不是简单的通过h关联,因为对数的参数求和不能被因式分解。如果假设Ph是相对平滑的,每一个Mel滤波器频带内卷积噪声的变化很小。 $$\eqalign{ & \sum\limits_{k = 0}^{N - 1} {{F_{jk}}{P_x}[k]} = \sum\limits_{k = 0}^{N - 1} {{F_{jk}}{P_s}[k]} {P_h}[k] \approx \cr & {P_h}[{k_j}]\sum\limits_{k = 0}^{N - 1} {{F_{jk}}{P_s}[k]} \cr} $$ 式中:Ph[kj]为{h(t)}在第j维滤波器中的能量谱。 $$\eqalign{ & {C_x}[i] = \sum\limits_{j = 1}^J {{G_{ij}}In({P_h}[{k_j}]} \sum\limits_{k = 0}^{N - 1} {{F_{jk}}{P_s}[k]} ) = \cr & \sum\limits_{j = 1}^J {{G_{ij}}(In{P_h}[{k_j}]} + \log [\sum\limits_{k = 0}^{N - 1} {{F_{jk}}{P_s}[k]} ) = \cr & \sum\limits_{j = 1}^J {{G_{ij}}(In{P_h}[{k_j}]} + In{Q_s}[j]) = \cr & {B_h}[i] + {C_s}[i] \cr} $$ 式中${B_h}[i] \buildrel \Delta \over = \sum _{j = 1}^J{G_{ij}}In{p_h}[{k_j}]$。
上述假设不排除在Ph在Mel频域滤波器的不同频带内产生变化,而只要求其在每个频带内的变化足够小,该假设要求设计良好的传输设备通带。然而在多噪声环境中,从声源到接收者的多路径反射可能导致峰谷的频率响应[16],不满足上述假设。因此第i维噪声和语音信号MFCC的差别与{h(t)},而与{s(t)}无关。也就是说,卷积噪声增加特征的偏置取决于瞬时的信道特性数值。如果进一步假设噪声是稳态的,对于MFCC,有
$$\eqalign{ & {{\bar C}_x}^{(\tau )}[i] = {C_x}^{(\tau )}[i] - {\mu _x}[i] = \cr & {C_x}^{(\tau )}[i] + {B_h}[i] - ({\mu _h}[i]) = \cr & {C_x}^{(\tau )}[i] - {\mu _s}[i] = {{\bar C}_s}^{(\tau )}[i],i = 0,1, \cdot \cdot \cdot ,I \cr} $$因此在稳态噪声和相对平滑的卷积噪声环境下,均值消减特征不会改变。从而在语句结构中,如果环境噪声是卷积类型并且在语句内是稳态的、平滑的,均值消减法是有效的。对均值消减的上述特性均建立在卷积噪声的基础上。对于加性噪声的分析将在后面三级滤波中进行分析。
3.2 方差归一化加性噪声不同于卷积噪声,在经过频域变换之后语音与加性噪声更加难以区分,为了更加方便地分析加性噪声环境下的语音信号,我们将含噪语音定义为 $$x(t;\gamma ) = s(t) + n(t;\gamma ) = s(t) + \gamma {n_o}(t)$$ 式中:加性噪声$n(t;\gamma ) \buildrel \Delta \over = \gamma n + \gamma {n_o}(t)$中的γ变量表示噪声的强度。本文首先分析加性噪声,然后分析语音信号。n(t;γ)和no(t)在Mel频域的对数特征表示为 $$\eqalign{ & In{Q_{n(\gamma )}}[j] = In(\sum\limits_{k = 0}^{N - 1} {{F_{jk}}} ({\gamma ^2}{P_{no}}[k])) = \cr & 2In|\gamma | + In(\sum\limits_{k = 0}^{N - 1} {{F_{jk}}} {P_{no}}[k]) = \cr & 2In|\gamma | + In{Q_{no}}[j] \cr} $$ 式中:Qn(γ)和Qno分别是n(t;γ)和no(t)的Mel频率谱表示,Mel倒谱系数可以表示为 $${C_{n(\gamma )}}[i] = \sum\limits_{j = 1}^J {{G_{jk}}} (2In|\gamma | + In{Q_{no}}[j]) = {C_{n(o)}}[i]$$ 式中:Cn(γ)和Cno分别是n(t;γ)和no(t)的倒谱,MFCC并没有衰减。含噪语音的功率谱为 $$\eqalign{ & {P_{x(\gamma )}}[k] = \cr & |S{[k]^2}|2\gamma |S[k]{N_o}[k]| + {\gamma ^2}|{N_o}{[k]^2}| = \cr & {P_s}[k] + 2\gamma |S[k]{N_o}[k]| + {\gamma ^2}{P_{no}}[k] \cr} $$ 式中:Px(γ)、Ps和Pno分别表示x(t;γ)、s(t)和no(t)的功率谱。由于Mel分级是线性运算,因此 $${Q_{x(\gamma )}}[j] = {Q_s}[j] + 2\gamma {Q_1}[j] + {\gamma ^2}{Q_{no}}[j]$$ 式中:${Q_1}[j] \buildrel \Delta \over = \sum _{k = 0}^{N - 1}{F_{jk}}|S[k]{N_o}[k]|$,Qx(γ)、Qs和Qno分别代表x(t;γ)、s(t)和no(t)的功率谱。Mel特征频谱的失真由两部分构成:一部分取决于噪声和语音信号,并且与γ成正比。另一部分只取决于噪声,并且与γ2成正比。根据式(5): $$\eqalign{ & {C_{x(\gamma )}}[i] = \sum\limits_{j = 1}^J {{G_{ij}}} In{Q_{x(\gamma )}}[j] = \cr & \sum\limits_{j = 1}^J {{G_{ij}}} In(Qs[j] + 2\gamma {Q_1})[j] + {\gamma ^2}{Q_{{n_o}}}[j]) = \cr & {C_s}[i] + \sum\limits_{j = 1}^J {{G_{ij}}} In(1 + 2\gamma {{{Q_1}[j]} \over {{Q_S}[j]}} + {\gamma ^2}{{{Q_{{n_o}}}[j]} \over {{Q_S}[j]}}) \cr & {C_s}[i] + \delta {C_{ij}}In(1 + 2\gamma {{{Q_1}[j]} \over {{Q_S}[j]}} + ){\gamma ^2}{{{Q_{{n_o}}}[j]} \over {{Q_S}[j]}} \cr} $$ 语音失真为
$$\delta {C_{x(\gamma )}}[i] \buildrel \Delta \over = \sum\limits_{j = 1}^J {{G_{ij}}} In(1 + 2\gamma {{{Q_1}[j]} \over {{Q_S}[j]}} + ){\gamma ^2}{{{Q_{{n_o}}}[j]} \over {{Q_S}[j]}}$$因此失真与语音信号s(t)和噪声n(t;γ)相关。一般强度的加性噪声影响与语音信号、噪声类型和噪声强度有着复杂的关系,因此加性噪声的滤波相对困难。当存在噪声语音数据样本时,可以考虑设计潜在的非线性变换来减小语音信号的失真。
均值消减法的使用无法弥补Ce2≠Cs造成的失真。处理含噪语音的方法有两种,一种是直接使用含噪语音样本,另一种是非线性变换去噪,直接使用含噪语音必须与测试语音噪声匹配。
加性噪声造成的语音信号失真不仅仅取决于噪声的加性增益,而与语音信号和噪声均相关,因此很难去除加性噪声。在低噪声环境下这种关联并不明显。高噪声环境下,在去除噪声增益项之后,本文应用了方差归一化法以弥补语音信号特征的衰减。由于存在γ-1的增益,在使用方差归一化法后,也无法得到零加性噪声的语音信号,因此处理后的语音特征很难满足要求。
3.3 时间序列滤波和加权自回归移动平均滤波本文首先分析了没有假设γ的语音信号失真。以此为依据建立了方差归一化法,并基于该方法的不足,分析低噪声$|\gamma | \ll 1$和高噪声$|\gamma | \gg 1$,这两种噪声情况都可以通过近似来简化。
1)低加性噪声
当$|\gamma | \ll 1$时,失真可以简化为 $$\delta {C_{x(\gamma )}}[i] \approx \sum\limits_{j = 1}^J {{G_{ij}}} In(1 + 2\gamma {{{Q_1}[j]} \over {{Q_S}[j]}} + ) \approx 2\gamma {C_{e1}}[i]$$ 式中:${C_{el}}[i] \buildrel \Delta \over = \sum _{j = 1}^J{G_{ij}}({Q_1}[j]/{Q_s}[j])$,并且ln(1+x)≈x。
2)高加性噪声
当$|\gamma | \gg 1$时,失真可简化为 $${Q_{X(\gamma )}}[i] \approx \sum\limits_{j = 1}^J {{G_{ij}}In} \left( {{\gamma ^2}\left( {{Q_{{n_o}}}[j] + {2 \over \gamma }{Q_i}[j]} \right)} \right)$$ 并且失真之后的MFCC特征近似为 $$\eqalign{ & {C_{X(\gamma )}}[i] \approx \sum\limits_{j = 1}^J {{G_{ij}}} \left( {{\gamma ^2}\left( {{Q_{{n_o}}}[j] + {2 \over \gamma }{Q_i}[j]} \right)} \right) \approx \cr & \sum\limits_{j = 1}^J {{G_{ij}}} In\left( {{\gamma ^2}{Q_{{n_o}}}\left( {1 + {2 \over \gamma }{{{Q_1}[j]} \over {{Q_{{n_o}}}[j]}}} \right)} \right) \approx \cr & \sum\limits_{j = 1}^J {{G_{ij}}} \left( {2In|\gamma | + {{{\mathop{\rm InQ}\nolimits} }_{{n_o}}}[j] + {2 \over \gamma }{{{Q_1}[j]} \over {{Q_{{n_o}}}[j]}}} \right) \approx \cr & {C_{{n_o}}}[i] + {2 \over \gamma }{C_{e2}}[i],i = 1,2, \cdot \cdot \cdot ,I \cr} $$ 式中:${C_{e2}}[i] \buildrel \Delta \over = \sum _{j = 1}^J{G_{ij}}({Q_1}[j]/{Q_{{n_o}}}[j])$。其倒谱主要与噪声no(t)相关,并且通过Ce2与语音强度成反比,倒谱特征的失真不只是偏置。由此,低噪声$|\gamma | \ll 1$和高噪声$|\gamma | \gg 1$时的噪声均反映了信号的不稳定性,因此强调语音动态特性和低频特性,将有助于加性噪声的去除。
人耳对语音的动态特征更为敏感,这种动态特性可以通过时间序列滤波实现。时间序列滤波之后的语音信号更接近真实语音信号。时间序列滤波器在语音信号静态特性的基础上,又兼顾了语音信号的动态特性,其使用达到了预期的目的。
由于人类的声音频率的结构性限制,发声时声道系统结构的改变有限,人类语音的重要信息主要是在低频段[17]。由于MFCC反映声道系统的特性,本文假设语音低频特征包含的信息更多。均值消减和方差归一化方法可以弥补能谱的下降,但却不能解决谱型平滑的问题。而加权自回归移动平均滤波由于强调了语音低频段的作用,并弱化了高频的影响。
4 实验设计及分析
实验数据库为用cooledit软件建立语音样本库。数据库规模为100人(50男50女),考虑时间的遍历性,同一段指令要求在不同的时间录制10遍。语音采样率16 kHz,单声道,Windows PCM编码格式,采样精度16位。噪声添加使用Noise-92库中的pink、volvo、destroyerengine(DE)、和white噪声,根据随机时间偏移与纯净语音信号混合,形成-5~20 dB范围内不同信噪比的数据库。
本文语音信号分帧采用交叠分段的法,每帧170个采样点,叠加步长为15个采样点,对信号进行特征提取得MFCC,设定特征维数为25。再以MFCC为基础,获得MVDA语音特征。
图 2,图 3,图 4,图 5,图 6,图 7,图 8,图 9,是语音“12345”在噪声环境下,MVDA特征向量的第一维和第D维特征。通过对比发现干净语音和不同信噪比的含噪语音的差异。均值消减和方差归化法使语音信号和含噪信号在同平均水平(均值消减)和总体规模(方差归一化法)的差异减小,然而差别依然明显。本文进一步使用了时间序列滤波和加权自回归移动平均滤波,差异进一步减小。
 |
| 图 6 语音特征C[D]噪声为20 dB时,MVDA后处理输出Fig. 6 The MVDA postprocessing output of voice features C[D] with noise of 20 dB |
 |
| 图 7 语音特征C[D]噪声为10 dB时,MVDA后处理输出Fig. 7 The MVDA postprocessing output of voice features C[D] with noise of 10 dB |
 |
| 图 8 语音特征C[D]噪声为0 dB时,MVDA后处理输出Fig. 8 The MVDA postprocessing output of voice features C[D] with noise of 0 dB |
 |
| 图 9 语音特征C[D]噪声为-5 dB时,MVDA后处理输出Fig. 9 The MVDA postprocessing output of voice features C[D] with noise of -5 dB |
然而使用视觉检查推断语音识别处理方法的不确定性总是存在的。为了便于比较,本文计算了语音信号特征和带噪语音信号特征的欧式距离,具体数值见表 1。可以分析得出,含噪语音特征和无噪语音信号特征的欧式距离均与噪声强度正相关。均值消减和方差归一化减小了含噪语音特征与无噪语音信号特征的欧式距离。最终,时间序列滤波和加权自回归移动平均滤波进一步减小了欧式距离。根据表 1,加权自回归移动平均滤波处理后的带噪语音更加接近真实的语音信号。
| 参数 | 20/dB | 10/dB | 0/dB | -10/dB |
| 均值消减 | 939 | 1 356 | 1 845 | 1 956 |
| 方差归一化 | 129 | 196 | 259 | 346 |
| 时间序列滤波 | 78 | 112 | 136 | 203 |
| 加权自回归移动平均 | 61 | 69 | 72 | 76 |
将MVDA与MFCC特征在自动语音识别系统下进行语音识别实验对比,实验结果如图 10 。可以得出,信噪比较高时,MFCC特征与MVDA特征的识别率基本相同,但随着信噪比降低,MVDA语音特征的效果更加显著。
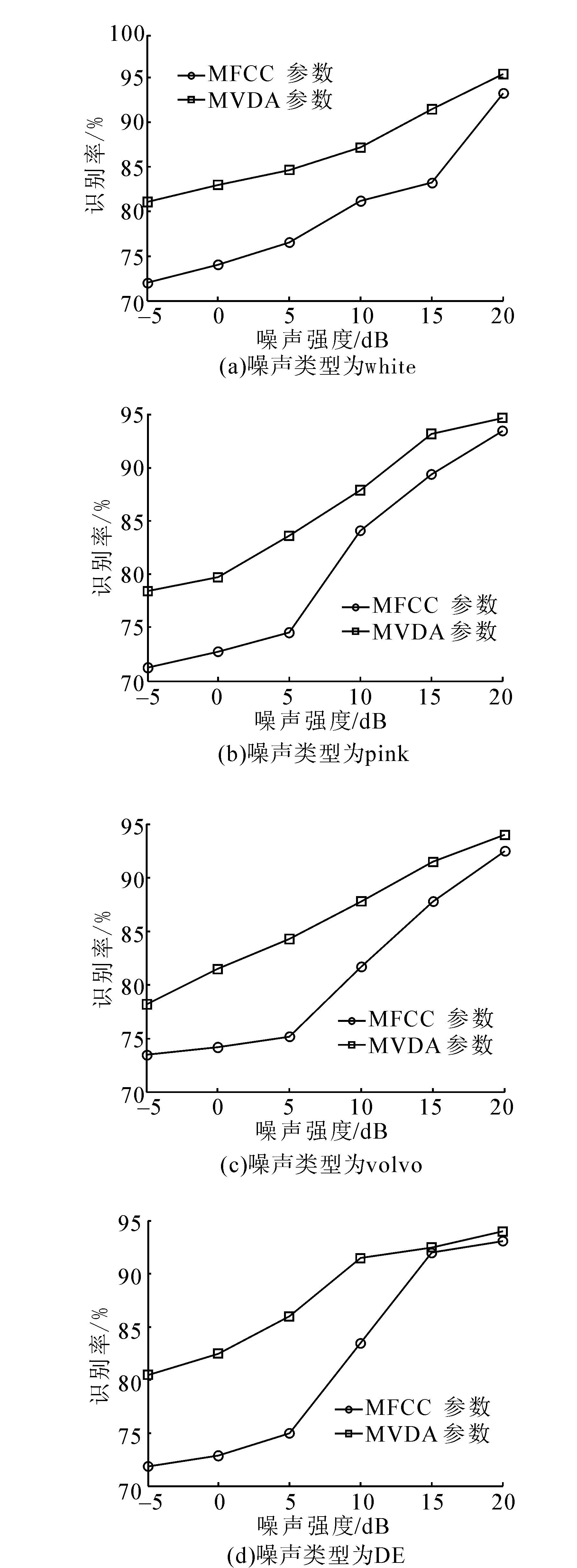 |
| 图 10 自动语音识别结果对比图Fig. 10 Comparison of automatic speech recognition results |
本文的分析主要基于加性噪声和卷积噪声环境下MFCC特征参数的失真,针对这一问题提出了MVDA语音特征提取法。分析得出实验效果与语音基本特征、滤波器的类型均相关。在使用MVDA滤波法后,相较于MFCC语音特征,自动语音识别系统在不同性噪比环境下的识别率提高了2.7%~15.0%。MVDA特征提取可以达到很多复杂去噪算法的效果,却可以减少系统对计算能力的要求,减小系统的时延。因此,MVDA后处理法可以在更小的计算代价下提高系统的鲁棒性,具有较高的实际应用价值。
| [1] | PALIWAL K K, BASU A. A speech enhancement method based on Kalman fltering[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Dallas, USA, 1997: 177-180. |
| [2] | GIBSON J D, KOO B, GRAY S D. Filtering of Colored Noise for Speech Enhancement and Coding[J]. IEEE Transactions on Signal Processing, 1991, 39(8): 1732-1742. |
| [3] | ZELINSKI R. A microphone array with adaptive post-filtering for noise reduction in reverberant rooms[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. New York, USA, 1998: 2578-2581. |
| [4] | MYLLYMAKI M, VIRTANEN T. Non-stationary noise model compensation in voice activity detection[C]//Proceedings of IEEE International Conference on Signal Processing Conference. Glasgow, Scotland, 2009: 2186-2190. |
| [5] | RAMFREZ J, SEGURA J C, BENFTEZ C, et al. Efficient voice activity detection algorithms using long-term speech information[J]. Speech communication, 2004, 42(3/4): 271-287. |
| [6] | CHOWDHURY M, SELOUANI S A, O'SHAUGHNESSY D. A soft computing approach to improve the robustness of on-line ASR in previously unseen highly non-stationary acoustic environments[C]//Proceedings of the 11th IEEE International Conference on Information Science, Signal Processing and their Applications. Montreal, Canada, 2012: 522-527. |
| [7] | GUPTA H A, RAJU A, ALWAN A. Non-linear dimension reduction of Gabor features for noise-robust ASR[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Florence, Italy, 2014: 1715-1719. |
| [8] | HANSEN J H L, VARADARAJAN V. Analysis and compensation of lombard speech across noise type and levels with application to in-set/out-of-set speaker recognition[J]. IEEE transactions on audio, speech, and language processing, 2009, 17(2): 366-378. |
| [9] | COOK G, ROBINSON T. Transcribing broadcast news with the 1997 abbot system[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Seattle, USA, 1998: 917-920. |
| [10] | KIM D S, LEE S Y, KIL R M. Auditory processing of speech signals for robust speech recognition in real-world noisy environments[J]. IEEE transactions on speech and audio processing, 1999, 7(1): 55-69. |
| [11] | HAIN T, WOODLAND P C, EVERMANN G, et al. New features in the CU-HTK system for transcription of conversational telephone speech[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Salt Lake City, UT, 2001(1): 57-60. |
| [12] | LIN S H, CHEN B, YEH Y M. Exploring the use of speech features and their corresponding distribution characteristics for robust speech recognition[J]. IEEE transactions on audio, speech, and language processing, 2009, 17(1): 84-94. |
| [13] | MORTIA S, UNOKI M, LU Xugang, et al. Robust voice activity detection based on concept of modulation transfer function in noisy reverberant environments[C]//Proceedings of International Symposium on Chinese Spoken Language Processing (ISCSLP). Singapore, 2014: 108-112. |
| [14] | CHANG J E, BAI J Y, ZENG Fangang. Unintelligible low frequency sound enhances simulated cochlear implant speech recognition in noise[J]. IEEe transactions on biomedical engineering, 2006, 53(12): 2598-2601. |
| [15] | BOLL S F. Suppression of acoustic noise in speech using spectral subtraction[J]. IEEE transactions on acoustics, speech, and signal processing, 1999, 27(2): 113-120. |
| [16] | MAMMONE R J, ZHANG Xiaoyu, RAMACHANDRAN R P. Robust speaker recognition: a feature-based approach[J]. IEEE signal processing magazine, 1996, 13(5): 58-71. |
| [17] | BOLL S F. Suppression of acoustic noise in speech using spectral subtraction[J]. IEEE transactions on acoustics, speech, and signal processing, 1999, 27(2): 113-120. |







