随着人类在海洋资源勘探和开发领域的不断加深，使得自主水下航行器(autonomous underwater vehicle,AUV)越来越得到重视，对其运动控制技术的研究也提出了新的挑战^{[1, 2, 3]}。由于自身重量和经济成本等因素，目前多数AUV采用更少推进器来完成多自由度耦合的运动控制，致使其成为典型二阶非完整约束的欠驱动系统^[4]。因此，针对一般类非完整速度约束的系统研究结论并不能直接应用到欠驱动航行器上^[5]，尤其是在系统建模参数不准确和存在未知环境扰动条件下，实现欠驱动AUV的轨迹跟踪控制更具有理论挑战与工程实际意义。

轨迹跟踪控制要求控制律能够导引AUV跟踪一条具有时变特性的参考轨迹，对时间条件具有强约束，因此与航迹点跟踪、路径跟踪控制相比，轨迹跟踪控制更加难以实现^[6]。文献^[7]基于Lyapunov直接法设计输出反馈控制器，同时实现了欠驱动AUV的全局渐近稳定及跟踪控制，但跟踪误差收敛半径依赖于环境扰动且无法通过系统增益进行适当调整，控制器具有较弱的鲁棒性。为解决系统参数不确定和外界扰动问题，鲁棒自适应控制^{[8, 9, 10, 11]}、滑模控制^{[12, 13, 14, 15, 16]}和神经网络^{[17, 18, 19]}等控制方法在水下航行器上得到大量应用。文献^[11]分别建立了五自由度和三自由度海流模型，采用反步法和级联系统理论设计控制器，但满意的跟踪效果极大地依赖参考模型，而且实际的设计与调试要比无模型方法复杂得多。文献^[16]利用滑模技术对系统参数变化的不敏感特性，将无抖振滑模控制器应用到全驱动AUV上，获得了较好的跟踪控制效果，但外界扰动未作考虑，且不能保证系统自适应估计项的有界性。文献^[18]利用DRFNN设计了六自由度AUV的自适应输出反馈控制器，虽然打破了对外界扰动及网络近似误差估计的限制条件，但系统在线自适应参数估计的计算量很大，不利于时变轨迹跟踪控制和实际工程应用。另一方面，反步法^{[20, 21, 22]}在解决欠驱动水下航行器的运动控制问题上也表现出一定优越性。文献^[20]利用虚拟速度量代替传统反步法中的姿态角误差变量，避免了控制律设计中的奇异值问题；文献^[21]采用仿生模型滤波反步法，解决了较大初始误差条件下速度跳变问题；文献^[22]基于二阶滤波反步法增加了系统对噪声的鲁棒性，但以上3种方法都未将系统内部参数不确定及外界扰动同时考虑，且自适应估计误差的有界性得不到保证。

通过以上分析，从工程应用角度出发，需要通过严谨且完整的理论分析，设计一种欠驱动AUV的轨迹跟踪控制器，满足对系统参数不确定及未知扰动的自适应和鲁棒性。除此之外，欠驱动AUV控制性能的实现，不能限制其初始条件、参考轨迹，且满足控制输入及速度约束。为此，本文首先将欠驱动AUV运动学特性线性化，设计满足速度约束的虚拟速度及航向角指令，解决了在较大初始误差条件下速度跳变问题，从而保证得到合理的控制输入，避免推进器饱和。其次，在动力学设计过程中，利用滑模对参数变化不敏感和对扰动具有良好的抑制特性，将文献^{[23, 24]}中滑模面加以改进完善，得到新的具有有界估计的自适应无抖振滑模控制器。且由于文献^{[23, 24]}中的理论存在一定缺陷，未定义航向角误差和角速度误差，所设计的控制器并不能保证航向角跟踪，本文就此给出了严谨的理论分析和仿真实验验证。仿真结果表明，即使存在较大初始误差、建模参数不准确及未知外界扰动条件下，本文所设计的控制器仍较之前方法具有更好的跟踪控制性能，且保证了控制输入及速度约束，更有利于实际工程应用。

1 欠驱动AUV的运动建模

目前，欠驱动AUV的轨迹跟踪控制大多解耦为水平面和垂直面运动，且以水平面控制器设计为主。本文考虑欠驱动AUV的平面轨迹跟踪控制，且满足如下假设条件: 1)忽略由于风、浪、流等外界扰动力引起的纵向、横摇和纵倾运动；2)AUV的惯性矢量矩阵和水动力阻尼矩阵是对角的，且高阶非线性水动力阻尼项可忽略；3)可用的控制输入仅有纵向力τ_u和偏航力矩τ_r，即AUV仅配备尾部推进器和垂直舵。建立该欠驱动AUV的运动学与动力学模型^[25]

1)AUV运动学模型

$$\left\{ \matrix{ \dot x = u\cos \psi - v\sin \psi \hfill \cr \dot y = u\sin \psi + v\cos \psi \hfill \cr \dot \psi = r \hfill \cr} \right.$$

(1)

2)AUV动力学模型

$$\left\{ \matrix{ \dot u = {{{m_{22}}} \over {{m_{11}}}}vr - {{{d_{11}}} \over {{m_{11}}}}u + {1 \over {{m_{11}}}}({\tau _{d1}} + {\tau _u}) \hfill \cr \dot v = {{{m_{11}}} \over {{m_{22}}}}ur - {{{d_{22}}} \over {{m_{22}}}}v + {1 \over {{m_{22}}}}{\tau _{d2}} \hfill \cr \dot r = {{({m_{22}} - {m_{11}})} \over {{m_{33}}}}uv - {{{d_{33}}} \over {{m_{33}}}}r + {1 \over {{m_{33}}}}({\tau _{d3}} + {\tau _r}) \hfill \cr} \right.$$

(2)

式中：${m_{11}} = m - {X_{\ddot u}}$，${m_{22}} = m - {Y_{\dot v}}$，${m_{33}} = {I_z} - {N_{\dot r}}$，${d_{11}} = {X_u} + {X_{|u|u}}|\dot u|$，${d_{22}} = {Y_v} + {Y_{|v|v}}|v|$，${d_{33}} = {N_r} + {N_{|r|r}}|r|$。状态变量(x,y,ψ)分别表示航行器在地面坐标系下的位置和航向角；(u,v,r)分别表示载体坐标系下AUV的纵向速度、横向速度和偏航角速度；m和m_(·)分别表示AUV的惯性质量和包含流体作用下的惯性质量，I_z为绕z轴的转动惯量；X_(·)、Y_(·)和N_(·)为粘性流体水动力系数；d_(·)为非线性水动力阻尼项；τ_(·)和τ_d(·)分别为AUV的控制输入和外界扰动力作用在载体坐标系下的分量。考虑到实际航行器的控制输入及速度限制，本文做出如下假设:

假设1 欠驱动AUV的控制输入及速度约束满足:|τ_u|≤τ_umax，|τ_r|≤τ_rmax，|u|≤u_max，|v|≤v_max和|r|≤r_max。

2 轨迹跟踪控制器设计 2.1 虚拟参考信号的设计

本文的设计目标是实现欠驱动AUV的平面轨迹跟踪控制，可能存在较大的初始误差条件、系统建模不准确及未知外界扰动情况。如何避免常规反步法中，虚拟速度设计直接跟位置误差变量相关，容易引起速度跳变，导致控制器输入饱和，是本节需解决的重点问题。航行器的平面参考轨迹由式(3)产生，即

$$\left\{ \matrix{ {{\dot x}_d} = {u_d}\cos {\psi _d} - {v_d}\sin {\psi _d} \hfill \cr {{\dot y}_d} = {u_d}\sin {\psi _d} - {v_d}\cos {\psi _d} \hfill \cr {{\dot \psi }_d} = {r_d} \hfill \cr} \right.$$

(3)

显然，根据假设1的条件，参考轨迹需满足下面的假设，具体论证稍后给出。

假设2 参考轨迹的速度u_d、v_d和r_d需满足:|u_d|+|v_d|≤u_max和|r_d|≤r_max。

首先，定义AUV的位姿跟踪误差为

$${x_e} = x - {x_d},{y_e} = y - {y_d},{\psi _e} = \psi - {\psi _d}$$

(4)

对位置误差求导，结合式(1)和(3)得到，

$$\eqalign{ & {{\dot x}_e} + {k_p}\tanh ({{\bar k}_p}{x_e}) = X \cr & {{\dot y}_e} + {k_p}\tanh ({{\bar k}_p}{y_e}) = Y \cr} $$

(5)

式中：k_p和${\bar k_p}$均为待设计的正常数，且 $$\eqalign{ & X = u\cos \psi - v\sin \psi - {u_d}\cos {\psi _d} + \cr & {v_d}\sin {\psi _d} + {k_p}\tanh ({{\bar k}_p}{x_e}) \cr & Y = u\sin \psi + v\cos \psi - {u_d}\sin {\psi _d} - \cr & {v_d}\cos {\psi _d} + {k_p}\tanh ({{\bar k}_p}{y_e}) \cr} $$ 定义新的误差变量e_x和e_y为

$$\left. {\left[ \matrix{ {e_x} \hfill \cr {e_y} \hfill \cr} \right.} \right]{\left[ {\matrix{ {\cos {\psi _d} - } & {\sin {\psi _d}} \cr {\sin {\psi _d}} & {\cos {\psi _d}} \cr } } \right]^{ - 1}}\left. {\left[ \matrix{ X \hfill \cr Y \hfill \cr} \right.} \right]$$

(6)

则e_x和e_y收敛到零，意味着x_e和y_e也收敛到零。根据式(6)，进一步整理得到

$$\left. {\left[ \matrix{ {e_x} \hfill \cr {e_y} \hfill \cr} \right.} \right]\left[ {\matrix{ {\cos {\psi _e} - } & {\sin {\psi _e}} \cr {\sin {\psi _e}} & {\cos {\psi _e}} \cr } } \right]\left. {\left[ \matrix{ u \hfill \cr v \hfill \cr} \right.} \right] - \left. {\left[ \matrix{ {\bar X} \hfill \cr {\bar Y} \hfill \cr} \right.} \right]$$

(7)

式中：

$$\eqalign{ & \bar X = {u_d} - \cos {\psi _d}{k_p}\tanh ({{\bar k}_p}{x_e}) - \cr & sin{\psi _d}{k_p}\tanh ({{\bar k}_p}{y_e}) \cr & \bar Y = {u_d} + sin{\psi _d}{k_p}\tanh ({{\bar k}_p}{x_e}) - \cr & \cos {\psi _d}{k_p}\tanh ({{\bar k}_p}{y_e}) \cr} $$

为得到速度u和v的虚拟控制量，将式(7)进一步变换，得到，

$$\eqalign{ & {\left[ {\matrix{ {\cos {\psi _e} - \sin {\psi _e}} \cr {\sin {\psi _e}\cos {\psi _e}} \cr } } \right]^{ - 1}}\left[ {\matrix{ {{e_x}} \cr {{e_y}} \cr } } \right] = \cr & \left[ {\matrix{ {u - \bar X\cos {\psi _e} - \bar Y\sin {\psi _e}} \cr {v + \bar X\sin {\psi _e} - \bar Y\cos {\psi _e}} \cr } } \right] \cr} $$

(8)

从式(8)可以很容易得到虚拟速度控制量u_c和v_c如式(9)所示，这也正是文献^{[23, 24]}中的控制器设计思路。虽然位置跟踪可以实现，但航向跟踪并不能保证，例如跟踪控制出现反向，这一点在本文仿真对比实验中得到进一步验证。所以，本文采用纵向速度u_c和航向角ψ_c作为虚拟控制量，从动力学模型(2)可以看出，这样设计控制器可以更好地实现位置与航向跟踪控制。

虚拟速度控制量设计为

$$\eqalign{ & {u_{e = }}\cos {\psi _{ec}}\bar X + \sin {\psi _{ec}}\bar Y \cr & {v_e} = - \sin {\psi _{ec}}\bar X + \cos {\psi _{ec}}\bar Y \cr} $$

(9)

式中：ψ_ec=ψ_c-ψ_d。为得到航向角ψ_c的控制设计，可根据式(7)，令e_x和e_y都为零，先得到航向角误差虚拟量：

$${\psi _{ec}} = \theta - \varphi {\rm{ 或}}{\psi _{ec}} = \pi + \theta - \varphi {\rm{ }}$$

(10)

式中：$\theta = arclan(\bar X/\bar Y)$和φ=arctan(v/u)。当期望速度u_d为正值时，ψ_ec=θ-φ；当u_d为负值时，ψ_ec=π+θ-φ。至此，虚拟速度控制量u_c和航向角ψ_c总结为

$$\eqalign{ & {u_e} = cos{\psi _{ec}}\bar X + \sin {\psi _{ec}}\bar Y \cr & {\psi _c} = {\psi _{ec}} + {\psi _d} \cr & {\psi _{ec}} = \theta - \varphi 或{\psi _{ec}} = \pi + \theta - \varphi \cr} $$

(11)

通过上述分析可知，当u=u_c和ψ=ψ_c，即可实现位置与航向跟踪控制。

2.2 滑模控制器设计

接下来，需要设计控制器τ_u和τ_r实现速度u和航向角ψ分别跟踪虚拟参考信号u_c和ψ_c。根据上述分析，需要对文献^{[23, 24]}中滑模面设计加以改进完善，首先考虑纵向速度控制，取滑模面S₁为

$${S_1} = {u_e} + {\lambda _1}{u_e} + {\lambda _2}\smallint {u_e}$$

(12)

式中：u_e=u-u_c，λ₁为正常数。对式(12)求导：

$${\ddot u_e} + {{{\lambda _1}} \over {{m_{11}}}}({m_{22}}vr - {d_{11}}u + {\tau _{d1}} + {\tau _u} - {m_{11}}{u_e})$$

考虑到系统建模不准确，可能引起控制器性能极度下降，定义系统不确定项f₁为 $$\eqalign{ & {f_1} = ({m_{11}} - {{\hat m}_{11}})({{\dot u}_e} - {{{{\ddot u}_e}} \over {{\lambda _1}}} - {{{\lambda _2}} \over {{\lambda _1}}}{u_e}) - \cr & ({m_{22}} - {{\hat m}_{22}})vr + ({d_{11}} - {{\hat d}_{11}})u \cr} $$ 控制器τ_u设计为

$$\eqalign{ & {\tau _u} = {{\hat m}_{11}}({{\dot u}_c} - {{{{\ddot u}_e}} \over {{\lambda _1}}} - {{{\lambda _2}} \over {{\lambda _1}}}{u_e}) - {{\hat m}_{22}}ur + \cr & {{\hat d}_{11}}u + {{\hat \smallint }_1} - {k_1}{S_1} - {B_1} \cr} $$

(14)

式中：考虑到计算${{{\ddot u}_e}}$的复杂性，采用反馈控制量${\ddot u_e} = - {k_u}{\dot u_e}$。${\hat \smallint _1}$为不确定项f₁的估计值，k₁为正常数，B_i(i=1,2)为鲁棒项，定义为

$${B_i} = \left\{ \matrix{ {{\hat \delta }_i}{{{S_i}} \over {|{S_i}|}},{S_i} \ne 0 \hfill \cr 0,{S_i} = 0 \hfill \cr} \right.$$

(15)

式中：${{\hat \delta }_1}$为有界扰动δ₁的估计值，即|τ_d1|≤δ₁。设计的控制器自适应律为

\[\begin{align} & {{{\dot{\hat{f}}}}_{1}}=-{{\Gamma }_{{{f}_{1}}}}{{S}_{1}}-{{\sigma }_{{{f}_{1}}}}{{\Gamma }_{{{f}_{1}}}}{{{\hat{f}}}_{1}} \\ & {{{\dot{\hat{\delta }}}}_{1}}={{\Gamma }_{{{\delta }_{1}}}}|{{S}_{1}}|-{{\sigma }_{{{\delta }_{1}}}}{{\Gamma }_{{{\delta }_{1}}}}|{{{\hat{\delta }}}_{1}}\text{ } \\ \end{align}\]

(16)

式中：Γ_f1、Γ_δ1为待设计正常数。σ_fi、σ_δi(i=1,2)为控制器切换参数：

$$\eqalign{ & {\sigma _{fi}} = \left\{ \matrix{ 0,|{f_i}| \le {N_{fo}} \hfill \cr {\sigma _{f0}}({{|{f_i}|} \over {{N_{f0}}}} - 1),{N_{f0}} \le |{f_i}| \hfill \cr {\sigma _{f0}},|{f_i}| \ge 2{N_{f0}} \hfill \cr} \right. \le 2{N_{f0}} \cr & {\sigma _{\delta i}} = \left\{ \matrix{ 0,|{\delta _i}| \le {N_{\delta o}} \hfill \cr {\sigma _{\delta o}}({{|{\delta _i}|} \over {{N_{\delta o}}}} - 1),{N_{\delta 0}} \le |{\delta _i}| \hfill \cr {\sigma _{\delta o}},|{\sigma _i}| \ge 2{N_{\delta o}} \hfill \cr} \right. \le 2{N_{\delta 0}} \cr} $$

(17)

式中：N_β0、N_δ0、σ_β0和σ_δ0均为正常数。下面验证控制器τ_u能够实现纵向速度控制。选取Lyapunov函数为

\[{{V}_{1}}=\frac{1}{2{{\lambda }_{1}}}{{m}_{11}}S_{1}^{2}+\frac{1}{2}\Gamma _{{{f}_{1}}}^{-1}{{\tilde{f}}_{1}}^{2}+\frac{1}{2}\Gamma _{{{\delta }_{1}}}^{-1}{{\tilde{\delta }}_{1}}^{2}\]

(18)

式中：${\tilde f_1} = {f_1} - {\hat f_1}$，${\tilde \delta _1} = {\delta _1} - {\hat \delta _1}$。对式(8)求导得到：

$${\dot V_1} \le - {k_1}S_1^2 + {\sigma _{{f_1}}}{\tilde f_1}{\hat f_1} + {\sigma _{{\delta _1}}}{\tilde \delta _1}{\hat \delta _1}$$

(19)

因此，纵向速度跟踪误差和自适应估计误差将渐近收敛到原点附近的一个小的邻域内。具体理论分析证明将在下面的稳定性分析中给出。

然后，考虑航向角和角速度跟踪控制，取滑模面S₂为

$${S_2} = {r_e} + {e_\psi } + {\lambda _3}\smallint ({r_e} + {e_\psi })$$

(20)

式中：r_e=r-r_d，e_ψ=ψ-ψ_c=ψ_e-ψ_ec，λ₃为正常数。同样，对式(20)求导，得到

$$\eqalign{ & {{\dot S}_2} = {1 \over {{m_{33}}}}[({m_{11}} - {m_{22}})uv - {d_{33}}r + {\tau _{d3}} + {\tau _r} - {m_{33}}{{\dot r}_d}] + \cr & {{\dot e}_\psi } + {\lambda _3}\smallint ({r_e} + {e_\psi }) \cr} $$

(21)

定义系统不确定项f₂为

$${f_2} = ({m_{33}} - {\hat m_{33}})({\dot r_d} - {\dot e_\psi } - {\lambda _3}({r_e} + {e_\psi })$$

(22)

控制器τ_r设计为

$$\eqalign{ & {\tau _r} = {{\hat m}_{33}}[{{\dot r}_d} - {{\dot e}_\psi } - {\lambda _3}({r_e} + {e_\psi })] - ({{\hat m}_{11}} - {{\hat m}_{22}})uv + \cr & {{\hat d}_{33}}r + {{\hat f}_2} - {k_2}{S_2} - {B_2} \cr} $$

(23)

式中：${{\hat f}_2}$为不确定项f₂的估计值，k₂为待设计的正常数，B₂为鲁棒项，定义如式(15)。${{\hat \delta }_2}$为有界扰动δ₂的估计值，即|τ_d3|≤δ₂。设计控制器自适应律为

\[\begin{align} & {{{\dot{\hat{f}}}}_{2}}=-{{\Gamma }_{{{f}_{2}}}}{{S}_{2}}-{{\sigma }_{{{f}_{2}}}}{{\Gamma }_{{{f}_{2}}}}{{{\hat{f}}}_{2}} \\ & {{{\dot{\hat{\delta }}}}_{2}}={{\Gamma }_{{{\delta }_{2}}}}|{{S}_{2}}|-{{\sigma }_{{{\delta }_{2}}}}{{\Gamma }_{{{\delta }_{2}}}}{{{\hat{\delta }}}_{2}} \\ \end{align}\]

(24)

式中：Γ_f2和Γ_δ2为待设计的正常数，控制器切换参数如式(17)中定义。下面进一步验证控制器τ_r能够实现航向角及角速度跟踪控制，选取Lyapunov函数为

$${V_2} = {1 \over 2}{m_{33}}S_2^2 + {1 \over 2}\Gamma _{{f_2}}^{ - 1}{\tilde f_2}^2 + {1 \over 2}\Gamma _{{\delta _2}}^{ - 1}{\tilde \delta _2}^2$$

(25)

式中：${{\tilde f}_2} = {f_2} - {{\hat f}_2}$，${{\tilde \delta }_2} = {\delta _2} - {{\hat \delta }_2}$。对式(25)求导，得到

$${\dot V_2} \le - {k_2}S_2^2 + {\sigma _{{f_2}}}{\tilde f_2}{\hat f_2} + {\sigma _{{\delta _2}}}{\tilde \delta _2}{\hat \delta _2}$$

(26)

因此，航向角和角速度跟踪误差都将收敛到原点附近的一个小的邻域。

3 稳定性分析

定理1 对给定AUV参考轨迹如式(3)，满足假设条件1和2,虚拟控制量如式(11)，控制器设计如式(14)和(23)，自适应律为(16)和(24)，以及鲁棒控制采用式(15)和(17)，通过合理的选择控制器参数k_p、${\bar k_p}$、k₁、k₂、k_u、Γ_f1、Γ_f2、Γ_δ1、Γ_δ2、σ_f1、σ_f2、σ_δ1和σ_δ2、实现欠驱动AUV轨迹跟踪误差的全局一致最终有界，且满足控制输入及速度约束条件。

证明 首先，给出速度跟踪误差的收敛性证明。根据上述控制器设计分析，构造Lyapunov函数V₃=V₁+V₂，对其求导，得到

$$\eqalign{ & {{\dot V}_3} = {{\dot V}_1} + {{\dot V}_2} \le \cr & - {k_1}S_2^2 + \sum\limits_{i = 1,2} {({\sigma _{{f_i}}}} {{\tilde f}_i}{{\hat f}_i} + {\sigma _{\delta i}}{{\tilde \delta }_i}{{\hat \delta }_i}) \cr} $$

(27)

利用表达式

$$\eqalign{ & {\sigma _{{f_i}}}{f_i}{{\hat f}_i} = {\sigma _{fi}}{{\tilde f}_i}({f_i} - {{\tilde f}_i}) \le \cr & - {\sigma _{fi}}{{\tilde f}^2}_i + {\sigma _{fi}}({{{{\tilde f}^2}_i + {f_i}^2} \over 2}) \le \cr & - {1 \over 2}{\sigma _{{f_i}}}{{\tilde f}^2}_i + {1 \over 2}{\sigma _{{f_i}}}{f_i}^2 \cr & {\sigma _{{\delta _i}}}{\delta _i}^T{{\hat \delta }^T}_i = ({\delta _i} - {{\hat \delta }_i}) \le \cr & - {\sigma _{{\delta _i}}}{{\tilde \delta }^2}_i + {\sigma _{{\delta _i}}}({{{{\tilde \delta }^2}_i + {\delta ^2}_i} \over 2}) \le \cr & - {1 \over 2}{\sigma _{\delta i}}{{\tilde \delta }^2}_i + {1 \over 2}{\sigma _{\delta i}}{\delta _i}^2 \cr} $$

(28)

根据式(17)，可知

$$\eqalign{ & {\sigma _{{f_i}}}{f_i}^2 \le 4{\sigma _{f0}}{N_{f0}} + {\sigma _{f0}}{f_i}^2 \cr & {\sigma _{{\delta _i}}}{\delta _i}^2 \le 4{\sigma _{{\delta _0}}}{N_{{\delta _0}}} + {\sigma _{{\delta _0}}}{\delta _i}^2 \cr} $$

(29)

结合式(28)和(29)，对式(27)整理得到

$$\eqalign{ & {{\dot V}_3} \le - {k_1}S_1^2 - {k_2}S_2^2 - {1 \over 2}\sum\limits_{i = 1,2} {\left( {{\sigma _{{f_i}}}{{\tilde f}^2}_i + {\sigma _{{\delta _i}}}{{\tilde \delta }^2}_i} \right)} + \cr & \sum\limits_{i = 1,2} {\left( {{\sigma _{{f_0}}}{f^2}_i + {\sigma _{{\delta _0}}}{\delta ^2}_i} \right)} + 4{\sigma _{{\beta _0}}}{N_{{f_0}}} + 4{\sigma _{{\delta _0}}}{N_{{\delta _0}}} \le \cr & - \mu {V_3} + C \cr & \mu = \min \{ 2{k_1}{\lambda _1},2{k_2},{{{\sigma _{{f_i}}}} \over {{\lambda _{\max }}({\Gamma _{fi}}^{ - 1})}},{{{\sigma _{{\delta _i}}}} \over {{\lambda _{\max }}({\Gamma _{\delta i}}^{ - 1})}}\} \cr & C = 4{\sigma _{fo}}{N_{{f_0}}} + 4{\sigma _{\delta o}}{N_{\delta 0}} + \sum\limits_{i = 1,2} {\left( {{\sigma _{{f_0}}}{f^2}_i + {\sigma _{{\delta _0}}}{\delta ^2}_i} \right)} \cr} $$

(30)

对式(30)进一步整理得到

$$0 \le {V_3}\left( t \right) \le {V_3}\left( 0 \right){e^{ - w}} + C/\mu $$

(31)

因此，系统的速度跟踪误差、航向角跟踪误差以及自适应估计误差均收敛到原点附近的一个小的邻域内，且收敛半径可通过适当增大式(30)中的增益值μ来减小。

接下来，进一步验证速度跟踪控制量的有界性及横向速度v跟踪误差的收敛性。

1)速度u的有界性:根据上述分析，速度u在控制器τ_u下可实现速度跟踪，即u=u_c，所以虚拟速度控制量u_c有界，即可保证速度u的有界性。根据式(11)得到，

$$\eqalign{ & |{u_c}| = |cos{\psi _{ec}}\bar X + sin{\psi _{ec}}\bar Y| \le \cr & |{u_d}| + |{v_d}| + \sqrt {2{k_p}} \cr} $$

(32)

根据假设1，|u_c|≤u_max，所以控制参数k_p应满足$0 < {k_p} \le {k_{pamx}} = {{{u_{\max }} - |{u_d}| - |{v_d}|} \over {\sqrt 2 }}$，保证了虚拟速度控制量u_c的有界性，同时也验证了假设条件2。

2)速度r的有界性:根据控制器设计，角速度r在控制器τ_r下可实现速度跟踪，即r=r_d，而参考轨迹是有界的，所以角速度r有界。

3)速度v的有界性:根据AUV动力学模型(2)，速度u、r和扰动项τ_d2均有界，所以速度v有界。

4)横向速度跟踪误差v_e的收敛性:定义横向速度误差v_e=v-v_c。根据虚拟控制量航向角ψ_ec=θ-φ，或ψ_ec=π+θ-φ可知：

$$\tan {\psi _{ec}} = {{\bar Yu - \bar Xv} \over {\bar Xu + \bar Yv}}$$

(33)

进一步整理，得

$$v = {v_e} + {T_u}{u_e}$$

(34)

式中：${T_u} = {{\cos {\psi _{ec}}\bar Y - \sin {\psi _{ec}}\bar X} \over {\cos {\psi _{ec}}\bar X + \sin {\psi _{ec}}\bar Y}}$。所以要保证横向速度误差v_e收敛，主要验证Τ_u是否有界。而根据非线性理论，Τ_u的有界性可根据两点保证:1)Τ_uu_e有界；2)当u_e=0时，Τ_uu_e=0。第一点可由v和v_c有界，根据式(34)保证Τ_uu_e有界；针对第二点，已知u_e=0和e_ψ=0，则式(8)等于零，即横向速度v=v_c，再结合式(34)可知，Τ_uu_e=0。综上所述，Τ_u有界，v_e=Τ_uu_e保证了横向速度误差的收敛性。

最后，验证位置跟踪误差的收敛性。针对外环控制系统，我们假设速度控制环已完成很好跟踪效果，即u=u_c，v=v_c和r=r_d，且e_ψ=0，即ψ_e=ψ_ec。根据位置误差定义 $$\eqalign{ & {{\dot x}_e} = \dot x - {{\dot x}_d} = \cr & u\cos \psi - v\sin \psi - {u_d}\cos {\psi _d} + \sin {\psi _d} = \cr & \left( {\cos {\psi _e}\bar X + \sin {\psi _e}\bar Y} \right)\cos \psi - ( - \sin {\psi _e}\bar X + \cr & \cos {\psi _e}\bar Y)\sin \psi - {u_d}\cos {\psi _d} + {v_d}\sin {\psi _d} = \cr & - {k_p}\tanh ({{\bar k}_p}{x_e}) \cr & {y_e} = \dot y - {{\dot y}_d} = \cr & u\sin \psi + v\cos \psi - {u_d}\sin {\psi _d} - {v_d}\cos {\psi _d} = \cr & (\cos {\psi _e}\bar X + \sin {\psi _e}\bar Y)\sin \psi + ( - \sin {\psi _e}\bar X + \cr & \cos {\psi _e}\bar Y)\cos \psi - {u_d}\sin {\psi _d} - {v_d}\cos {\psi _d} = \cr & - {k_p}\tanh ({{\bar k}_p}{y_e}) \cr} $$

所以，位置跟踪控制误差x_e和y_e均收敛到零。而航向跟踪误差ψ_e=∫r_e，根据滑模面S₂的设计，可以保证收敛到零，同时ψ_ec=ψ_e-e_ψ也收敛到零。再结合式(11)，可知虚拟速度量u_c和v_c分别收敛到u_d和v_d。综上所述，本文给出了完整且严谨的轨迹跟踪控制系统稳定性分析证明，保证了跟踪误差的全局一致最终有界。

4 仿真实验结果与分析

为验证本文所提出的控制器性能，采用文献^[27]中的欠驱动AUV模型作为实验对象。模型参数为:m₁₁=215 kg，m₂₂=265 kg，m₃₃=80 kgm²，d₁₁=70+100|u|，kg/s，d₂₂=100+200|v|，kg/s，d₃₃=50+100|r|，kgm²/s。仿真实验包括如下两种: 1)圆形轨迹跟踪x_d=100sin(0.01t)，y_d=100cos(0.01t)；2)正弦轨迹跟踪x_d=t，y_d=100sin(0.01t)。两种控制方案中都存在较大初始误差，初始速度(u(0),v(0),r(0))=(0,0,0)，且控制输入和速度约束条件为τ_umax=1 000 N，τ_rmax=1 000 Nm，u_max=5 m/s，v_max=3 m/s，r_max=2 rad/s。为满足上述约束条件，选取控制器参数为k_p=1，k-_p=0.1，λ₁=2，λ₂=1，λ₃=1，k₁=100，k₂=50，k_u=1，Γ_fi=20，Γ_δi=10，σ_f0=0.01，σ_δ0=0.01。

为更好验证控制器的鲁棒性，假设系统存在10%的建模误差，即仿真中对名义模型参数同时增加10%作为实际参数。且采用同文献^[26]中相似的方式产生随机扰动力，即τ_di=0.1m_iirand(·)，i=1,2,3，其中rand(·)为高斯随机噪声，取值区间为[0,1]，然后分别作用在AUV动力学模型(2)中各自由度上。为了更好地说明本文控制器不仅能在较大初始误差条件，系统参数不准确及未知外界扰动下具有良好的跟踪控制性能，还能解决文献^{[23, 24]}中无法实现航向跟踪控制问题。对文献^[24]中的控制器采用同样上述约束条件进行对比实验仿真验证。

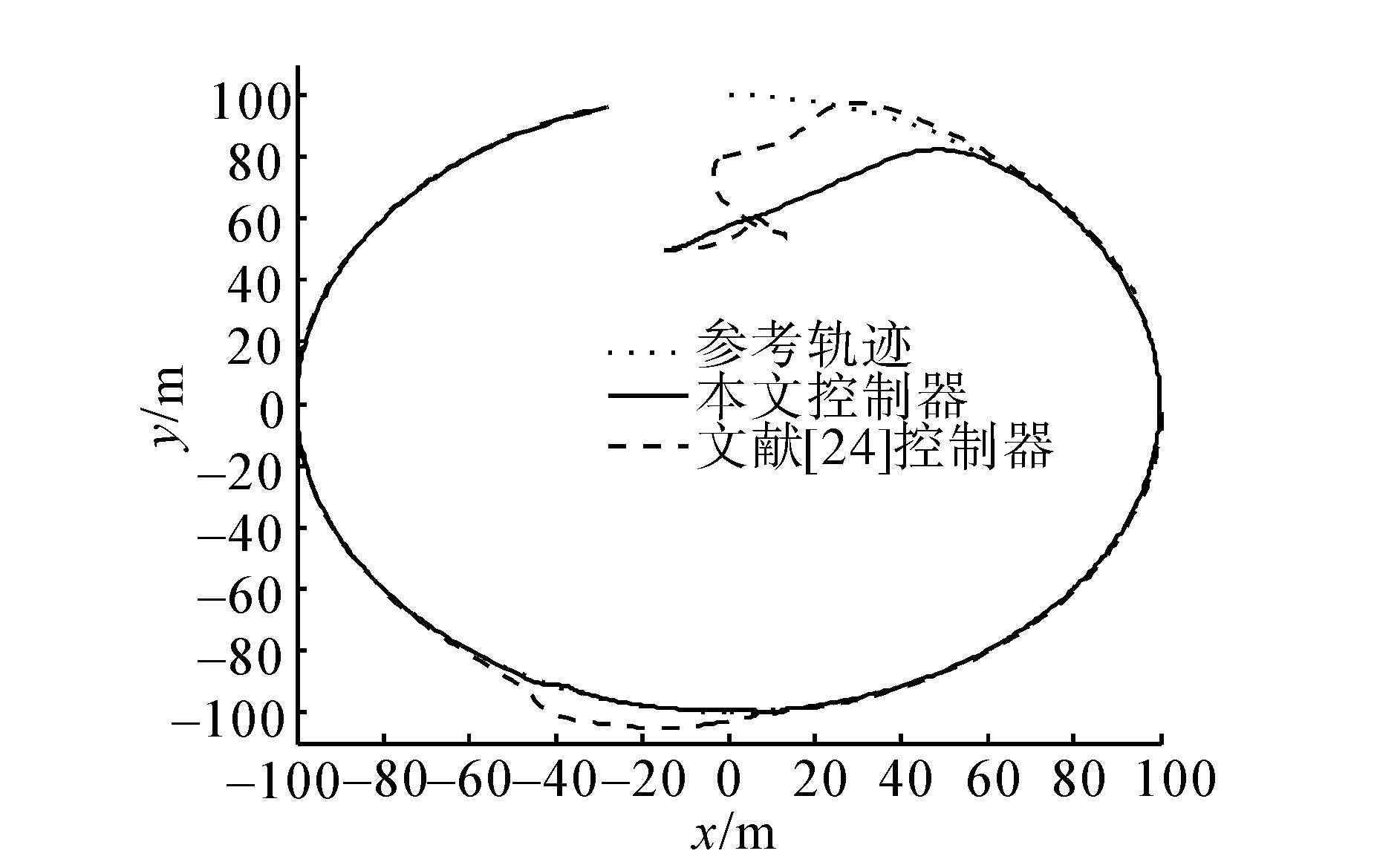
图 1给出了欠驱动AUV在两种控制方法下实现圆形轨迹跟踪控制的实验结果。

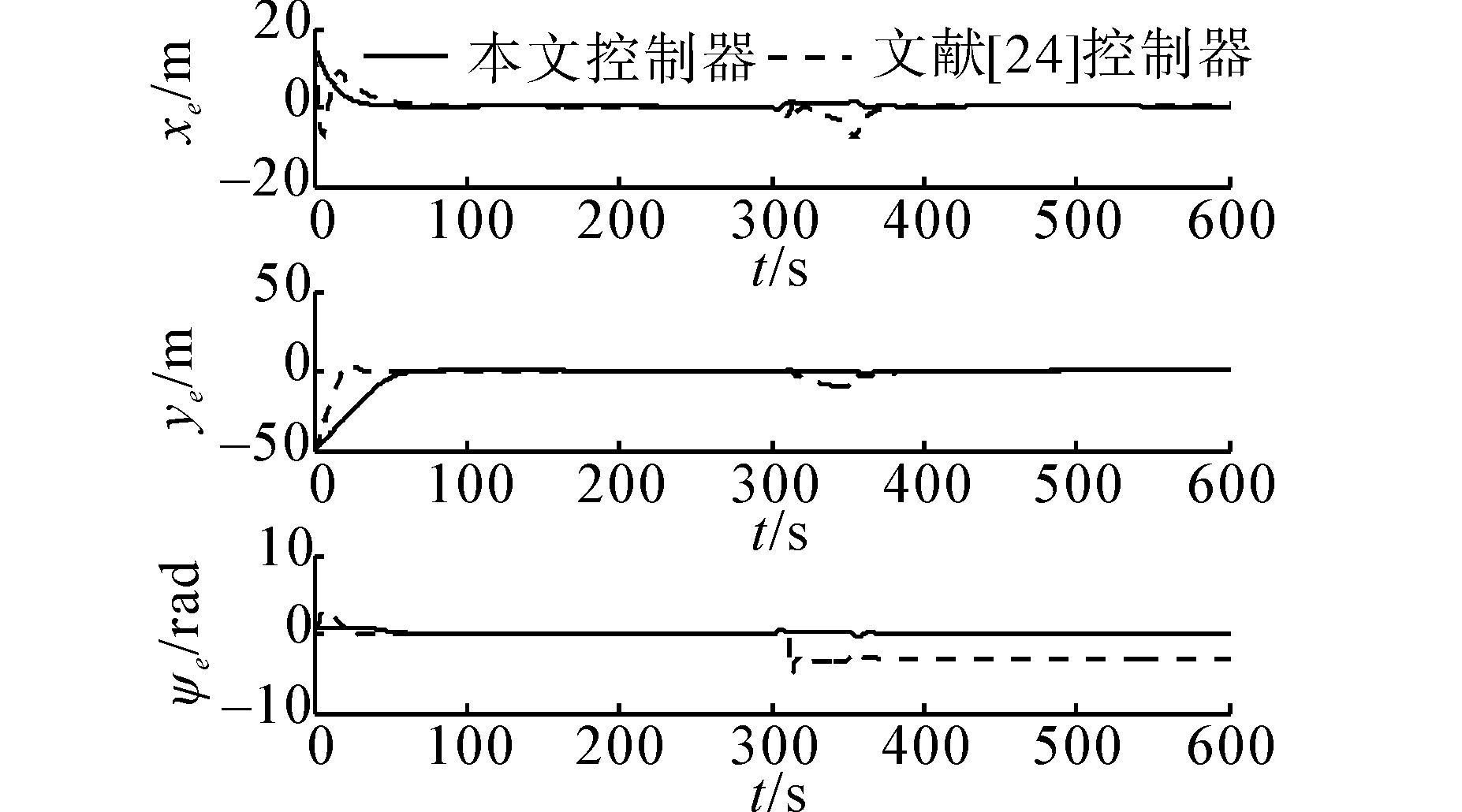
从图 1,图 2,图 3,图 4,中可以看出，虽然欠驱动AUV具有较大的初始误差条件、建模不准确、未知随机扰动以及控制输入和速度约束，但相比文献^[24]的控制方法，本文所提出的控制器明显具有更佳控制效果。

位置和航向跟踪误差充分小且收敛更加平滑、速度更快，此外，本文在初始误差较大情况下，速度跟踪并未出现文献^[24]中的速度跳变现象，避免了控制输入饱和。为了更好验证控制器的鲁棒性，在仿真时间300~350 s的时间段，额外50 N的定常扰动作用到AUV的三自由度运动学模型上。很明显之前方法在没有控制输入和速度约束下能够实现轨迹跟踪控制，但遭受重大扰动后，跟踪控制性能极度下降，甚至航向跟踪出现反向，导致纵向速度出现负值，即倒退行进，这并不符合轨迹跟踪控制要求。总之，以上跟踪控制结果充分体现了本文控制器的有效性和鲁棒性。

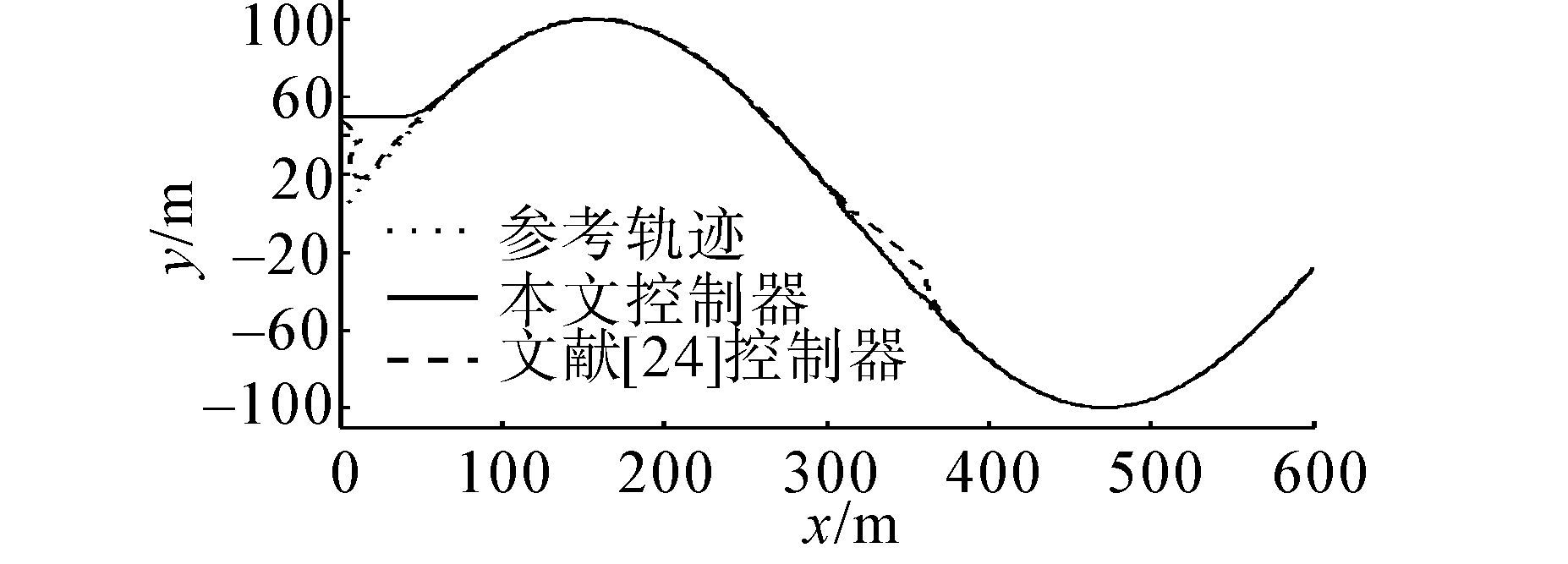
图 5为欠驱动AUV跟踪具有时变速度的正弦曲线。同样在具有较大初始误差条件下，本文控制器的跟踪控制效果，较文献^[24]中方法相比，明显具有更好的动态响应和足够充分小的跟踪误差，如图 6,图 7,图 8。即使在300~350 s出现重大未知扰动，但位姿和速度跟踪响应平滑，未出现速度跳变和推进器饱和，充分体现了该控制器的强鲁棒性。而之前文献中未对航行器航向跟踪控制给出理论分析设计，无法保证航向跟踪控制，在该实验中得到充分论证。以上跟踪控制实验结果，充分体现了欠驱动AUV即使存在较大初始误差、系统模型不准确、未知外界扰动以及控制输入和速度约束情况，本文控制器仍然能够实现全局轨迹跟踪控制，满足实际工程应用需求。

5 结束语

本文针对欠驱动AUV存在较大初始误差、系统建模参数不准确、未知外界扰动以及控制输入和速度约束等问题，采用类似反步法设计过程，提出具有有界自适应估计的无抖振滑模控制器，解决了常规反步法中因大初始误差引起速度跳变问题，避免了推进器饱和，满足了控制输入和速度约束条件。而且，针对文献^[24]中滑模控制器无法保证航向跟踪控制的缺陷，设计了高阶积分滑模面，实现了跟踪误差控制系统的全局一致有界性。最后，基于Lyapunov稳定性理论给出了完整且严谨的理论分析证明，并在仿真对比实验中加以验证，充分体现了本文控制器的有效性和强鲁棒性，能更好地适用于实际工程应用，但本文仅设计了平面控制器，未来工作需进一步扩展到欠驱动AUV的三维空间轨迹跟踪控制。