聚类就是将物理或抽象的对象按照自己的某些属性聚集成类的过程,并尽可能使得类(或者簇)之间对象的差异程度最大,而类内(或者簇内)的相似程度达到最大。聚类过程没有先验知识指导,仅凭对象间的相似程度作为类属划分的准则,是无监督分类学习的一部分。最为经典的模糊聚类算法之一就是J.C.Bezdek教授在20世纪80年代提出的模糊c均值聚类算法[1],该算法被成功地应用到了在诸多问题的解决上。
随着科学技术的发展,数据库中的数据更新速度日益加快、数据容量不断增大,若仍然采用原来的聚类算法对这样的大规模数据进行聚类将产生以下几个问题:1)数据更新前得到的聚类结果可能与数据更新后的聚类结果不匹配;2)对更新后的数据进行重新聚类会导致较高的时间复杂度和计算资源的浪费;3)还可能由于系统内存不足的原因而导致该算法失效。鉴于这些问题,Fazli Can教授在1990年提出的增量式聚类算法[2]使得这些问题得以解决。所谓增量式聚类是指利用前期数据已取得的聚类结果,对新增数据进行分批或者逐批次地进行聚类的过程。研究增量式模糊聚类算法对于避免重复聚类造成的计算资源浪费,提高聚类性能等都具有十分重要的意义。
近几年,研究者们提出了很多关于增量式聚类的算法。这些算法大致可以被分为3类:1)对大数据进行随机抽样获取小样本进行计算,例如,L. Kaufman等提出的CLARA[3],S.Guha等[4]提出的CURE;2)按序将小样本加载进内存的单程算法(single-pass),具有代表性的有F. Can在文献[5]和[6]中提出的增量式算法;3)采取类图表结构的数据转换算法,如T. Zhang等提出的BIRCH[7]和R. Ng等[8]提出的CLARANS,对于增量式模糊聚类算法;B. U. Shankar等[9]提出了快速模糊c均值算法FFCM,T. Cheng[10]提出了多阶段的随机模糊c均值算法MRFCM,J. F. Kolen等[11]提出了随机抽样模糊c均值算法rsFCM,Dhanesh Kothari等[12]提出了将随机抽样的结果扩展到整个数据集上的扩展随机抽样模糊c均值算法rseFCM。除此之外,还有基于FCM的单程模糊c均值算法SPFCM[13]、在线模糊c均值算法OFCM[14],以及在这基础上发展的基于核的模糊c均值算法spkFCM和okFCM[15],Yangtao Wang等[16]提出的基于多重中心的增量式模糊聚类算法在相关性大数据上的应用。最近Böhm等[17]受到动力学中同步现象的启发提出了一种新颖的同步聚类算法Sync,但是这种算法在大规模数据集上的聚类受到了相当大的限制,基于此应文豪等[18]在此基础上提出了快速自适应同步聚类算法FAKCS。
传统的FCM算法对初始聚类中心敏感且容易陷入局部最优,同时也忽略了类间的相互影响。Jacek M. Leski对FCM算法进行了改进,提出了模糊c+p均值聚类算法FCPM,并采用了新的方法初始化聚类中心[19]。对于某一类的聚类中心,它能吸引属于该类的样本并排斥属于其他类的样本,这样更清楚地确定了样本的“归属”问题。对于小样本数据,FCPM算法可以保持不错的聚类性能,但其在大规模数据集上的聚类性能明显降低而且有较大的时间花费,甚至可能由于无法加载进内存而导致算法失效。对于以往的增量式模糊聚类算法,比如SPFCM算法和OFCM算法都是通过对样本加权以影响每个数据块产生的聚类中心,但数据块间聚类中心的相互影响程度不明显甚至可能会由于上一次聚类结果的加入而干扰新的数据进行聚类。为了解决以上问题,通过FCPM算法计算每个数据块的聚类中心,把离聚类中心最近的一些样本点连同聚类中心一起加入到下一个数据块中参与聚类,同时添加平衡项以提高聚类性能,文中提出了适合大规模数据集的增量式聚类算法IFCM(c+p)。
1 相关算法设N元样本集合X={x1,x2,…,xN},xk(k=1,2,…,N)表示其中的某一个样本,其中每一个样本都有D={d1,d2,…,dn}Rn一共n个特征,dj(j=1,2,…,n)表示其中的某一个特征。FCM算法将N个样本按照它所固有的特征划分成c簇,用μik表示第k个样本隶属于第i簇的程度,那么划分成c簇后得到的隶属度矩阵是U={μik}Rc×N,i∈[1,c],k∈[1,N]。对于模糊划分而言,所有的样本都需要满足下面的条件: \[\left\{ \begin{align} & {{M}_{feN}}=\left\{ U\in {{R}^{c\times N}}\left| {{\mu }_{ik}}\in \left[ 0,1 \right],\forall i\in \left[ 1,c \right],k\in \left[ 1,N \right] \right. \right\}; \\ & \sum\limits_{i=1}^{c}{{{\mu }_{ik}}=1,} \\ & \forall k\in \left[ 1,N \right];\sum\limits_{k=1}^{N}{{{\mu }_{ik}}\in \left( 0,N \right),\forall i\in \left[ 1,c \right]} \\ \end{align} \right.\]
由此可见,模糊划分矩阵U的每一列的和都必须等于1,这样才能确保每一个样本都能够被完整地划分到它所属的簇中。
通过使用欧式距离寻求最小均方误差,可以得到FCM模型的目标函数(其中m为模糊指数):
$$J\left( {U,V} \right) = {\sum\limits_{i = 1}^c {\sum\limits_{k = 1}^N {\mu _{ik}^m\left\| {{x_k} - {v_i}} \right\|} } ^2}$$
(1)
在式(1)的条件下通过拉格朗日乘子法可以得出隶属度矩阵U和聚类中心V的更新公式。由于篇幅有限,FCM算法的具体更新公式以及计算步骤在此不做赘述。
传统的FCM算法让聚类中心尽可能地靠近样本点,概率约束也只考虑了聚类中心之间的排斥力,所有的样本重要性相同,同时对初始聚类中心敏感、容易陷入局部最优,得到的聚类结果往往不理想。Jacek M. Leski考虑了类别间的相互影响,利用了新的方法初始化聚类中心,采用固定一类求其他类的方法,在FCM算法的基础上提出了模糊c+p均值聚类算法FCPM。
FCPM算法中来自其他类的样本对本类的聚类会产生影响,在某一类中,聚类中心应该吸引属于该类的样本,而排斥其他类的样本。设有c个聚类中心来自一类,而p个聚类中心来自另一类,该算法把N个样本划分成为c簇,可得目标函数为
$$\eqalign{
& J\left( {U,T,V} \right) = \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^N {\mu _{jk}^m} } {\left\| {{x_k} - {v_i}} \right\|^2} + \cr
& {\sum\limits_{j = 1}^p {\sum\limits_{k = 1}^N {\xi _{jk}^m\left\| {{x_k} - {z_j}} \right\|} } ^2} \cr} $$
(2)
$$\eqalign{
& \sum\limits_{i = 1}^c {{\mu _{ik}} + \sum\limits_{j = 1}^p {{\xi _{jk}} = 1,{\mu _{ik}} \in \left[ {0,1} \right]} } , \cr
& {\xi _{jk}} \in \left[ {0,1} \right],\forall k \in \left[ {1,N} \right] \cr} $$
(3)
利用拉格朗日乘子法,可以得到划分矩阵U、T以及聚类中心V的更新公式:
$$\eqalign{
& \mu ik = \frac{{{{\left\| {{x_k} - {v_i}} \right\|}^{\frac{2}{{1 - m}}}}}}{{\sum\limits_{l = 1}^c {{{\left\| {{x_k} - {v_i}} \right\|}^{\frac{2}{{1 - m}}}} + \sum\limits_{r = 1}^p {{{\left\| {{x_k} - {z_r}} \right\|}^{\frac{2}{{1 - m}}}}} } }} \cr
& \forall k \in \left[ {1,N} \right],i \in \left[ {1,c} \right] \cr} $$
(4)
$$\eqalign{
& {\xi _{jk}} = \frac{{{{\left\| {{x_k} - {z_j}} \right\|}^{\frac{2}{{1 - m}}}}}}{{\sum\limits_{l = 1}^c {{{\left\| {{x_k} - {v_l}} \right\|}^{\frac{2}{{1 - m}}}} + \sum\limits_{r = 1}^p {{{\left\| {{x_k} - {z_r}} \right\|}^{\frac{2}{{1 - m}}}}} } }} \cr
& \forall k \in \left[ {1,N} \right],j \in \left[ {1,p} \right] \cr} $$
(5)
$${v_i} = \frac{{\sum\limits_{k = 1}^N {\mu _{ik}^m{x_k}} }}{{\sum\limits_{k = 1}^N {\mu _{ik}^m} }},\forall i \in \left[ {1,c} \right]$$
(6)
针对FCM算法对初始聚类中心敏感的问题,FCPM算法采用了新的方法初始化聚类中心。通过该方法初始化未知类的聚类中心V,使用FCM算法初始化已知类的聚类中心Z,再依次通过式(4)、(5)和(6)获取模糊划分矩阵U和聚类中心V。文献[19]详细介绍了新的聚类中心初始化方法及FCPM算法,此处不再赘述。
如文献[19]所示,FCPM算法在模糊系统建模上得到了很好的应用。该算法采用新的初始化聚类中心的方法有效地避免了FCM算法对初始聚类中心敏感的问题,通过先确定已知类聚类中心来求未知类聚类中心的方法以提高算法的聚类性能。通过实验可以发现,FCPM算法对一类已知的小样本数据集有着不错的聚类性能,但对现实中的大规模数据集而言,该算法的聚类性能会下降、算法效率会大大降低甚至会由于样本过大而导致算法失效。基于这些问题,本文提出了适合大规模数据集的增量式模糊聚类算法IFCM(c+p)。
2 适合大规模数据集的增量式模糊聚类算法IFCM(c+p) 2.1 IFCM(c+p)算法在增量式模糊聚类算法中,对每一个数据块进行聚类的算法起着举足轻重的作用。针对以往基于FCM的增量式模糊聚类算法对初始聚类中心敏感的问题,文中采用了FCPM算法中提到的特别的方法初始化聚类中心。另外在传统的增量式模糊聚类算法中,不管是静态的还是动态的、单程的还是在线的、一个中心或者是多个中心(多个中心形成了一个约束对)等等的方法,都没有考虑数据块之间聚类中心的相互影响,提及的IFCM(c+p)算法很好地解决了这些问题。
为了增加数据块间聚类中心的相互影响程度,本文添加了一个平衡项$\alpha {\sum\limits_{i = 1}^c {\left\| {{v_i} - v_i^o} \right\|} ^2}$,其中α被称为平衡因子,往往它的取值与J(U,T,V)有关。由此,可以得到提及算法的目标函数:
$$\eqalign{
& J\left( {U,T,V,\alpha } \right) = J\left( {U,T,V} \right) + \alpha \sum\limits_{i = 1}^c {{{\left\| {{V_i} - V_i^o} \right\|}^2} = } \cr
& \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^N {\mu _{ik}^m} } {\left\| {{x_k} - {v_i}} \right\|^2} + \sum\limits_{j = 1}^p {\sum\limits_{k = 1}^N {\xi _{jk}^m{{\left\| {{x_k} - {z_j}} \right\|}^2} + } } \cr
& \alpha \sum\limits_{i = 1}^c {{{\left\| {{v_i} - v_i^o} \right\|}^2}} \cr} $$
(7)
下面采用拉格朗日极值法求模糊划分矩阵U、T以及聚类中心V的更新公式。
$$\eqalign{
& G\left( {U,T,V,\lambda } \right) = \cr
& J\left( {U,T,V,\alpha } \right) - \lambda (\sum\limits_{i = 1}^c {{\mu _{ik}} + \sum\limits_{j = 1}^p {{\xi _{jk}} - 1} } ) = \cr
& J\left( {U,T,V} \right) + \alpha {\sum\limits_{i = 1}^c {\left\| {{v_i} - v_i^o} \right\|} ^2} - \cr
& \lambda (\sum\limits_{i = 1}^c {{\mu _{ik}} + \sum\limits_{j = 1}^p {{\xi _{jk}} - 1) = } } \cr
& \sum\limits_{i = 1}^c {\mu _{ik}^m{{\left\| {{x_k} - {v_i}} \right\|}^2} + \sum\limits_{j = 1}^p {\xi _{jk}^m{{\left\| {{x_k} - {z_j}} \right\|}^2} + } } \cr
& \alpha \sum\limits_{i = 1}^c {{{\left\| {{v_i} - v_i^o} \right\|}^2} - \lambda (\sum\limits_{i = 1}^c {{\mu _{ik}} + \sum\limits_{j = 1}^p {{\xi _{jk}} - 1)} } } \cr
& \forall k \in \left[ {1,N} \right] \cr} $$
(8)
对G(U,T,V,λ)中的各个变量分别求偏导并令其等于零得:
\[\left\{ \begin{align}
& \frac{{{\partial }_{J}}_{(U,T,V,\lambda )}}{{{\partial }_{\mu ik}}}=m\sum\limits_{i=1}^{c}{\mu _{ik}^{m-1}}{{\left\| {{x}_{k}}-{{v}_{i}} \right\|}^{2}}-\lambda =0 \\
& \frac{{{\partial }_{J}}_{(U,T,V,\lambda )}}{{{\partial }_{\xi ik}}}=m\sum\limits_{i=1}^{c}{\xi _{jk}^{m-1}{{\left\| {{x}_{k}}-{{z}_{j}} \right\|}^{2}}-\lambda =0} \\
& \frac{{{\partial }_{J(U,T,V,\lambda )}}}{{{\partial }_{\lambda }}}=\sum\limits_{i=1}^{c}{{{\mu }_{ik}}+\sum\limits_{j=1}^{p}{{{\xi }_{jk}}-1=0}} \\
& \frac{{{\partial }_{J(U,T,V,\lambda )}}}{{{\partial }_{vi}}}=-2\sum\limits_{i=1}^{c}{\mu _{ik}^{m}\left\| {{x}_{k}}-{{v}_{i}} \right\|+} \\
& 2\alpha \sum\limits_{i=1}^{c}{\left\| {{v}_{i}}-v_{i}^{o} \right\|=0} \\
\end{align} \right.\]
(9)
通过(9)可以很容易地求出模糊划分矩阵的更新公式μik和ζjk,如式(4)、(5)所示。可以发现,模糊划分矩阵U和T与平衡因子α无关。
由式(9)第4个等式可得
$${v_i} = {{\sum\limits_{k = 1}^N {\mu _{ik}^m{x_k} + \alpha v_i^o} } \over {\sum\limits_{k = 1}^N {\mu _{ik}^m + \alpha } }},\forall i \in \left[ {1,c} \right]$$
(10)
从式(10)可以看出,根据平衡因子α是否等于0,又可以分为两种情况。
当α=0即不考虑数据块间聚类中心的相互影响时,在每一个数据块的聚类过程中,将某个数据块产生的聚类中心加入下一个数据块中参与聚类,为了增大对数据块间聚类效果的影响程度,把距聚类中心最近的n0个样本点也一同加入下一个数据块参与聚类,以此类推,直至计算出最后一个数据块的聚类中心,这个最终的聚类中心就是我们所要求的整个数据集的聚类中心。
α=0时的情况仅仅考虑了某一数据块的聚类中心及其周围的n0个样本点对下一个数据块的聚类性能的影响,这样得出的聚类效果并不理想。为了提高聚类性能,应该考虑数据块间聚类中心的相互影响即α≠0时的情况,此时平衡项的加入很好地提高了聚类性能。
如下所述为IFCM(c+p)算法的具体计算步骤。
输入:X,c,p,m,n0,ε;
输出:聚类中心V。
1)把样本集x随机划分成大小相等的s个子集即x={X1,X2,…,Xs};
2)定义一个空的集合Xincre和Xnear;
3)遍历所有的数据块获取聚类中心:for l=1,2,…,s
①初始化未知类和已知类的聚类中心V、Z;
②把从上一数据块获得的样本Xincre添加到当前数据块,即Xl={Xl∪Xincre};
③使用式(4)、(5)和(10)计算当前数据块的聚类中心Vl;
④取出距当前数据块的聚类中心最近的n0个样本点存入Xnear中;
⑤把聚类中心Vl及其附近的n0个样本点存入Xincre中,即Xincre={Vl∪Xnear}; end for
上述算法步骤2)的Xincre用以存放每一个数据块产生的聚类中心及其附近的n0个样本点Xnear,3)对这s个数据块进行遍历,求其聚类中心。3)中的主要迭代过程在每个数据块中使用FCPM算法计算聚类中心,使用欧氏距离求距聚类中心最近的n0个样本点,并把它们一同加入到下一个数据块中去参与聚类。注意在初始化聚类中心时,采用前面提到的FCPM算法的初始化方法对已知类和未知类的聚类中心Z、V进行初始化,聚类中心V和模糊隶属度矩阵U的更新公式分别为(10)、(4),‖·‖表示求欧氏距离。FCPM算法的迭代终止于聚类中心的连续变化值的Frobenius范数小于ε。整个IFCM(c+p)算法终止于所有的数据块遍历结束并获得最终的聚类中心。
2.2 算法的可行性分析正如传统的增量式聚类算法一样,IFCM(c+p)算法对每个数据块进行聚类。在IFCM(c+p)算法中,没有添加平衡项时,将每个数据块的c个聚类中心及距其最近的n0个样本点作为一次聚类结果的历史信息加入到新增数据中,即每次都有c+n0个样本点加入到新增数据中参与聚类,那么这些历史信息的加入势必将影响新增数据的聚类效果。如果历史信息恰好位于新增数据附近,则其聚类效果将变好,如果历史信息远离它们,历史信息的加入反而会导致一个很差的聚类效果。对于SPFCM算法和OFCM算法而言,它们通过添加样本权值以增加聚类效果,在一定程度上比仅仅添加历史信息得到的聚类效果要好,但也存在上面所提到的一些问题。为了克服以上问题,提到的IFCM(c+p)算法添加了平衡项,通过平衡项中的平衡因子去改变数据块间聚类中心的相互影响程度,此时即便历史信息远离新增数据,通过合理调节平衡因子α的取值也可以使得聚类中心吸引它周围的新增数据,从而提高聚类效果。
2.3 算法复杂度文献[15]详细介绍了rseFCM、SPFCM算法的时间和空间复杂度,如表1所示,本文提到的FCPM及IFCM(c+p)算法的时间和空间复杂度也如表1所示。其中t表示非增量式算法的迭代次数,t'表示增量式算法中每个数据块的平均迭代次数,d表示数据集维数,c表示未知类的聚类个数,p表示已知类的聚类个数,s表示数据块的个数,n0表示在IFCM(c+p)算法中距每个数据块的聚类中心最近的样本点个数。
| 算法 | 时间复杂度 | 空间复杂度 |
| FCPM | O(tnd(c+p)+tc) | O(n(d+c+p)) |
| rseFCM | O(tc2dn/s) | O((d+c)n/s) |
| SPFCM | O(ndt′c2) | O((d+c)n/s) |
| IFCM(c+p) | O(t′nd(c+p)+t′c) | O((d+c+p+n0)n/s) |
如表1所示,本文提到的算法均在相同环境下运行,都对同一数据集X进行处理,时间复杂度都为O(n)。然而从第3部分的实验可以看出,各算法的运行时间存在着显著不同。对于增量式模糊聚类算法,由于它们在每个数据块的处理中能够快速收敛因而可以使得算法总的运行时间减少。
本文提到的增量式模糊聚类算法都是对数据进行分块处理,因此需要计算每个数据块所占用的空间即为n/s。如表1所示,同rseFCM和SPFCM算法相比,由于IFCM(c+p)算法需要存储聚类中心及其周围的一些样本,因此需要占用相对较多的存储空间,也就拥有相对高的空间复杂度。
3 相关实验研究 3.1 评价指标为了公正地对各聚类算法的聚类效果做出合理的评价,本文采用如下3种评价指标进行算法的性能分析。
3.1.1 算法运行时间的加速比speedup
该指标反映了聚类算法在指定数据集下运行时间的比较情况。定义加速比:
speedup=tfull/tincremental
2)归一化互信息(normalized mutual information,NMI)[20, 21] $${\rm N}{\rm M}{\rm I} = {{\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^c {N_i^j\log \left( {{{N \cdot N_i^j} \over {{N_i} \cdot {N_j}}}} \right)} } } \over {\sqrt {\sum\limits_{i = 1}^c {{N_i}\log \left( {{{{N_i}} \over N}} \right)} } \cdot \sqrt {\sum\limits_{j = 1}^c {{N_j}\log \left( {{{{N_j}} \over N}} \right)} } }}$$ 式中:N表示样本总数,Ni表示经本文聚类算法之后第i簇的样本总数,Nj表示真实数据集的第j类的样本总数,Nji表示第i簇与第j类的契合程度,即二者共有的样本总数。
3)芮氏指标(rand index,RI)[20, 21, 22] $$R{\rm I} = {{{f_{00}} + {f_{11}}} \over {N(N - 1)/2}}$$ 式中:f00表示样本点具有不同的类标签并且属于不同类的配对样本数目,f11则表示样本点具有相同的类标签并且属于同一类的配对样本数目,N表示样本总数。
以上NMI、RI两种指标,其取值范围均为[0, 1],且取值越靠近1越能反映该聚类算法在某数据集下的聚类效果越好,反之越靠近0则反映该聚类算法的聚类效果越差。加速比speedup越大反映了增量式聚类算法的运行时间越短。
3.2实验结果1)实验环境
本文所有的实验均在如表2的环境中进行。
| 结构 | 具体参数 |
| 操作系统 | Windows 7专业版64位 |
| 处理器 | Intel(R)Xeon(R)E5-1620 v2@3.7GHz |
| 运行内存 | 64G |
| 软件及版本 |
MATLAB 7.11.0 .584 (R2010b) |
2)实验数据集
实验所选取的数据集包括人工数据集2D15(http://www.uef.fi/en/sipu/datasets)、UCI(http://archive.ics.uci.edu/ml/datasets.html)、标准数据集waveform、forest和手写数字数据集MNIST(http://yann.lecun.com/exdb/mnist/)。各数据集的分布情况如表3。
| 数据集 | 大小 | 维数 | 类别数 |
| 2D15 | 5000 | 2 | 15 |
| waveform | 5000 | 21 | 3 |
| forest | 581012 | 54 | 7 |
| MNIST | 70000 | 784 | 10 |
MNIST数据集是手写数字集的一个子集,包含了70000张28 × 28 像素的数字0~9的图像,每个像素都在整数0~255之间取值。为加快运算,对MNIST数据集中的所有样本分别除以255进行归一化处理[15]。为方便计算,本文随机取forest的581000个样本进行计算。同样,对其他数据集也进行归一化处理以加快运算,即用每个特征的所有样本与该特征的最小值作差再除以该特征的最大值与最小值之差。
3)实验参数设置
本文中所有的参数都按如下取值:模糊指数m取2,最大迭代次数均为100,迭代终止参数ε取1e-3,聚类中心附近的样本点个数n0取5,其中数据集2D15、waveform重复试验50次,由于数据集MNIST和forest样本过大,我们重复试验20次。数据块的大小应由用户指定,但在实验中,由于计算机内存受限,forest数据集的数据块大小依次取0.1%、0.5%、1%、2.5%、5%,其余均按照整个数据集的1%、2.5%、5%、10%、25%、50%随机抽取。取MNIST数据集70%的样本、forest数据集10%的样本参与FCPM算法的聚类。平衡因子α的具体取值也由用户指定,但是必须在给定的经验值范围内取值,本文中的所有α值均是在多次重复实验中,提到的聚类指标的均值达到最好的时候的取值。我们计算提到的几种算法在各个数据集上的NMI和RI的最值、均值以及标准差,其中均值反映了算法的平均聚类性能,最值和标准差反映了算法的稳定鲁棒性。
4)算法性能比较
本文采用SPFCM算法和rseFCM算法同IFCM(c+p)算法在聚类性能和加速比上进行比较。
1)各算法在数据集上的聚类性能比较
各算法在指定数据集下的聚类性能如表4~11所示,其中最优均值已用黑体标出。
| 样本大小 | IFCM(c+p)(α=2.1) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 1% | 0.4107 | 0.0233 | 0.4091 | 0.0026 | 0.3909 | 0.0074 | 0.3078 | 0.0037 |
| 0.3855 | 0.4398 | 0.3980 | 0.4173 | 0.3567 | 0.4248 | 0.3061 | 0.3332 | |
| 2.50% | 0.4329 | 0.0062 | 0.3484 | 0 | 0.3613 | 0.0018 | 0.3199 | 0.0040 |
| 0.4320 | 0.4756 | 0.3472 | 0.3485 | 0.3488 | 0.3616 | 0.3185 | 0.3474 | |
| 5% | 0.4194 | 0.0079 | 0.3345 | 0.0010 | 0.3369 | 0 | 0.3463 | 0 |
| 0.3872 | 0.4220 | 0.3343 | 0.3415 | 0.3365 | 0.3371 | 0.3463 | 0.3464 | |
| 10% | 0.3411 | 0 | 0.3332 | 0 | 0.3259 | 0 | 0.2964 | 0 |
| 0.3409 | 0.3415 | 0.3299 | 0.3333 | 0.3258 | 0.3263 | 0.2958 | 0.2968 | |
| 25% | 0.3350 | 0.0049 | 0.3308 | 0 | 0.3245 | 0 | 0.3362 | 0 |
| 0.3025 | 0.3442 | 0.3307 | 0.3309 | 0.3237 | 0.3251 | 0.3361 | 0.3363 | |
| 35% | 0.3656 | 0 | 0.3253 | 0 | 0.3311 | 0 | 0.3259 | 0 |
| 0.3617 | 0.3660 | 0.3251 | 0.3254 | 0.3311 | 0.3312 | 0.3257 | 0.3265 | |
| 50% | 0.3556 | 0 | 0.3354 | 0 | 0.3361 | 0 | 0.3241 | 0 |
| 0.3554 | 0.3558 | 0.3353 | 0.3354 | 0.3349 | 0.3365 | 0.3239 | 0.3246 | |
| FCPM | 0.3285 | 0.0081 | ||||||
| 0.2892 | 0.3302 | |||||||
| 样本大小 | IFCM(c+p)(α=2.1) | IFCM(c+p)(α=0) | SPFCM | |||||
| rseFCM | ||||||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 1% | 0.9399 | 0.0244 | 0.8438 | 0.0312 | 0.9260 | 0.0164 | 0.8688 | 0.0213 |
| 0.8785 | 0.9870 | 0.7699 | 0.9055 | 0.8972 | 0.9494 | 0.8195 | 0.9137 | |
| 2.50% | 0.9348 | 0.0100 | 0.8695 | 0.0193 | 0.9302 | 0.0163 | 0.8965 | 0.0252 |
| 0.9000 | 0.9553 | 0.8278 | 0.9238 | 0.9042 | 0.9513 | 0.8298 | 0.9410 | |
| 5% | 0.9519 | 0.0159 | 0.9123 | 0.0086 | 0.943 | 0.0165 | 0.9035 | 0.0202 |
| 0.9155 | 0.9715 | 0.8783 | 0.9262 | 0.9055 | 0.9606 | 0.8652 | 0.9433 | |
| 10% | 0.9369 | 0.0084 | 0.8775 | 0.0047 | 0.9313 | 0.0115 | 0.9200 | 0.0193 |
| 0.9284 | 0.9507 | 0.8717 | 0.8882 | 0.8906 | 0.9449 | 0.8776 | 0.9432 | |
| 25% | 0.9260 | 0 | 0.8646 | 0.0130 | 0.9222 | 0.0147 | 0.9294 | 0.0195 |
| 0.9255 | 0.9263 | 0.8259 | 0.8713 | 0.8958 | 0.9405 | 0.8866 | 0.9509 | |
| 35% | 0.9137 | 0.0248 | 0.9097 | 0 | 0.9270 | 0.0157 | 0.9214 | 0.0208 |
| 0.8952 | 0.9474 | 0.9087 | 0.9104 | 0.8992 | 0.9431 | 0.8652 | 0.9438 | |
| 50% | 0.9118 | 0 | 0.9079 | 0 | 0.921 | 0.0174 | 0.9169 | 0.02 |
| 0.9111 | 0.9122 | 0.9076 | 0.9083 | 0.8839 | 0.9439 | 0.8696 | 0.9425 | |
| FCPM | 0.8607 | 0 | ||||||
| 0.8604 | 0.8608 | |||||||
| 样本大小 | IFCM(c+p)(α=160) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 1% | 0.3139 | 0 | 0.2447 | 0 | 0.2246 | 0.0709 | — | — |
| 0.3139 | 0.3139 | 0.2447 | 0.2447 | 0.1337 | 0.3345 | — | — | |
| 2.50% | 0.2606 | 0 | 0.2390 | 0 | 0.2588 | 0.0310 | — | — |
| 0.2606 | 0.2606 | 0.2390 | 0.2390 | 0.1915 | 0.3173 | — | — | |
| 5% | 0.2974 | 0 | 0.1646 | 0 | 0.2424 | 0.0423 | — | — |
| 0.2974 | 0.2974 | 0.1646 | 0.1646 | 0.1417 | 0.2987 | — | — | |
| 10% | 0.3217 | 0 | 0.2089 | 0 | 0.2299 | 0 | — | — |
| 0.3217 | 0.3217 | 0.2089 | 0.2089 | 0.2296 | 0.2301 | — | — | |
| 25% | 0.2634 | 0 | 0.2180 | 0 | 0.1818 | 0 | — | — |
| 0.2634 | 0.2634 | 0.2180 | 0.2180 | 0.1807 | 0.1832 | — | — | |
| 35% | 0.3309 | 0 | 0.1712 | 0 | 0.2027 | 0.0131 | — | — |
| 0.3309 | 0.3309 | 0.1712 | 0.1712 | 0.1763 | 0.2328 | — | — | |
| 50% | 0.2135 | 0 | 0.2072 | 0 | 0.1744 | 0.0188 | — | — |
| 0.2135 | 0.2135 | 0.2072 | 0.2072 | 0.1632 | 0.2037 | — | — | |
| FCPM(70%) | 0.1723 | 0 | ||||||
| 0.1723 | 0.1723 | |||||||
| 样本大小 | IFCM(c+p)(α=21) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 0.1% | 0.1593 | 0.0016 | 0.1036 | 0 | 0.1161 | 0.0089 | — | — |
| 0.1583 | 0.1631 | 0.1036 | 0.1036 | 0.1042 | 0.1370 | — | — | |
| 0.5% | 0.1123 | 0 | 0.1016 | 0 | 0.1012 | 0.0049 | — | — |
| 0.1123 | 0.1125 | 0.1016 | 0.1016 | 0.0943 | 0.1143 | — | — | |
| 1% | 0.1264 | 0 | 0.1055 | 0 | 0.1102 | 0.0056 | — | — |
| 0.1260 | 0.1273 | 0.1055 | 0.1055 | 0.1036 | 0.1225 | — | — | |
| 2.50% | 0.1077 | 0 | 0.1064 | 0 | 0.1003 | 0.0030 | — | — |
| 0.1077 | 0.1077 | 0.1064 | 0.1064 | 0.0963 | 0.1075 | — | — | |
| 5% | 0.1092 | 0 | 0.1021 | 0 | 0.1025 | 0.0050 | — | — |
| 0.1053 | 0.1094 | 0.1021 | 0.1021 | 0.0988 | 0.1113 | — | — | |
| FCPM(10%) | 0.1015 | 0 | ||||||
| 0.1015 | 0.1015 | |||||||
| 样本大小 | IFCM(c+p)(α=2.1) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 0.1% | 0.7023 | 0.0095 | 0.6804 | 0.0018 | 0.6691 | 0.3301 | 0.6572 | 0.0018 |
| 0.6841 | 0.7176 | 0.6767 | 0.6873 | 0.6637 | 0.6882 | 0.65656 | 0.6697 | |
| 2.50% | 0.6890 | 0.0015 | 0.6638 | 0 | 0.6743 | 0 | 0.6633 | 0.0028 |
| 0.6888 | 0.6996 | 0.6627 | 0.6639 | 0.6743 | 0.6748 | 0.6623 | 0.6824 | |
| 5% | 0.7009 | 0.0024 | 0.6659 | 0 | 0.6625 | 0 | 0.6658 | 0 |
| 0.6911 | 0.7017 | 0.6658 | 0.6674 | 0.6622 | 0.6626 | 0.6658 | 0.6659 | |
| 10% | 0.6666 | 0 | 0.6651 | 0 | 0.6619 | 0 | 0.6531 | 0 |
| 0.6664 | 0.6708 | 0.6632 | 0.6652 | 0.6619 | 0.6621 | 0.6529 | 0.6533 | |
| 25% | 0.6643 | 0.0018 | 0.6633 | 0 | 0.6613 | 0 | 0.6633 | 0 |
| 0.6537 | 0.6693 | 0.6633 | 0.6634 | 0.6612 | 0.6615 | 0.6632 | 0.6634 | |
| 35% | 0.6702 | 0 | 0.6640 | 0 | 0.6632 | 0 | 0.6623 | 0.0024 |
| 0.6692 | 0.6703 | 0.6638 | 0.664 | 0.6632 | 0.6633 | 0.6619 | 0.6790 | |
| 50% | 0.6699 | 0 | 0.6644 | 0 | 0.6651 | 0 | 0.6607 | 0 |
| 0.6698 | 0.6701 | 0.6644 | 0.6644 | 0.6648 | 0.6652 | 0.6607 | 0.6608 | |
| FCPM | 0.6622 | 0.0027 | ||||||
| 0.6492 | 0.6627 | |||||||
| 样本大小 | IFCM(c+p)(α=0.2) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 0.1% | 0.979 | 0.0097 | 0.9383 | 0.0127 | 0.9755 | 0.006 | 0.9697 | 0.0079 |
| 0.9559 | 0.9976 | 0.9135 | 0.9665 | 0.9665 | 0.9837 | 0.9504 | 0.9856 | |
| 2.50% | 0.9848 | 0.0024 | 0.9605 | 0.0064 | 0.9818 | 0.0054 | 0.9773 | 0.008 |
| 0.9756 | 0.9879 | 0.9461 | 0.9761 | 0.9717 | 0.9881 | 0.9561 | 0.9912 | |
| 5% | 0.9897 | 0.0050 | 0.9767 | 0.0030 | 0.9869 | 0.0049 | 0.9787 | 0.0064 |
| 0.9792 | 0.9946 | 0.9648 | 0.9805 | 0.9773 | 0.9916 | 0.9647 | 0.9915 | |
| 10% | 0.9871 | 0.0033 | 0.9701 | 0.0019 | 0.9864 | 0.0039 | 0.9836 | 0.0067 |
| 0.9836 | 0.9914 | 0.9677 | 0.9720 | 0.9743 | 0.9903 | 0.9687 | 0.9917 | |
| 25% | 0.9835 | 0 | 0.9651 | 0.0029 | 0.9849 | 0.0052 | 0.9861 | 0.0061 |
| 0.9834 | 0.9835 | 0.9566 | 0.9678 | 0.9763 | 0.9901 | 0.9708 | 0.9929 | |
| 35% | 0.9832 | 0.0066 | 0.9804 | 0 | 0.9860 | 0.0053 | 0.9844 | 0.0067 |
| 0.9783 | 0.9932 | 0.9803 | 0.9805 | 0.9779 | 0.9910 | 0.9672 | 0.9917 | |
| 50% | 0.9801 | 0 | 0.9812 | 0 | 0.9842 | 0.0056 | 0.9829 | 0.0066 |
| 0.9799 | 0.9802 | 0.9812 | 0.9813 | 0.9711 | 0.9915 | 0.9652 | 0.9913 | |
| FCPM | 0.9683 | 0 | ||||||
| 0.9683 | 0.9684 | |||||||
| 样本大小 | IFCM(c+p)(α=160) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | avg. | std. | |
| 0.1% | 0.7864 | 0 | 0.7222 | 0 | 0.7352 | 0.0961 | — | — |
| 0.7864 | 0.7864 | 0.7222 | 0.7222 | 0.6063 | 0.8401 | — | — | |
| 2.50% | 0.7935 | 0 | 0.7123 | 0 | 0.7924 | 0.0336 | — | — |
| 0.7935 | 0.7935 | 0.7123 | 0.7123 | 0.6925 | 0.8300 | — | — | |
| 5% | 0.7576 | 0 | 0.6129 | 0 | 0.7541 | 0.0503 | — | — |
| 0.7576 | 0.7576 | 0.6129 | 0.6129 | 0.6448 | 0.8221 | — | — | |
| 10% | 0.8117 | 0 | 0.6429 | 0 | 0.7947 | 0 | — | — |
| 0.8117 | 0.8117 | 0.6429 | 0.6429 | 0.7944 | 0.7953 | — | — | |
| 25% | 0.7375 | 0 | 0.6608 | 0 | 0.7274 | 0 | — | — |
| 0.7375 | 0.7375 | 0.6608 | 0.6608 | 0.7270 | 0.7289 | — | — | |
| 35% | 0.7729 | 0 | 0.6076 | 0 | 0.7215 | 0.0099 | — | — |
| 0.7729 | 0.7729 | 0.6076 | 0.6076 | 0.7032 | 0.7408 | — | — | |
| 50% | 0.6633 | 0 | 0.6612 | 0 | 0.6420 | 0.0224 | — | — |
| 0.6633 | 0.6633 | 0.6612 | 0.6612 | 0.6094 | 0.6916 | — | — | |
| FCPM(70%) | 0.6134 | 0 | ||||||
| 0.6134 | 0.6134 | |||||||
| 样本大小 | IFCM(c+p)(α=21) | IFCM(c+p)(α=0) | SPFCM | rseFCM | ||||
| avg. | std. | avg. | std. | avg. | std. | vg. | std. | |
| 0.1% | 0.5828 | 0 | 0.5697 | 0 | 0.5804 | 0.0122 | — | — |
| 0.5827 | 0.583 | 0.5697 | 0.5697 | 0.5616 | 0.6007 | — | — | |
| 0.5% | 0.5648 | 0 | 0.5608 | 0 | 0.5674 | 0 | — | — |
| 0.5648 | 0.5648 | 0.5608 | 0.5608 | 0.5583 | 0.587 | — | — | |
| 1% | 0.5737 | 0 | 0.5641 | 0 | 0.5728 | 0.0072 | — | — |
| 0.5737 | 0.5737 | 0.5641 | 0.5641 | 0.5643 | 0.5887 | — | — | |
| 2.50% | 0.5680 | 0 | 0.5640 | 0 | 0.5722 | 0.0093 | — | — |
| 0.5680 | 0.5680 | 0.5640 | 0.5640 | 0.5615 | 0.5904 | — | — | |
| 5% | 0.5696 | 0 | 0.5626 | 0 | 0.5688 | 0.0188 | — | — |
| 0.569 | 0.5696 | 0.5626 | 0.5626 | 0.5615 | 0.5941 | — | — | |
| FCPM(10%) | 0.5628 | 0 | ||||||
| 0.5628 | 0.5628 | |||||||
从各表中的实验结果对比发现,增量式模糊聚类算法的聚类性能均优于FCPM算法。在人工数据集2D15的聚类性能比较中发现数据块大小取25%、35%和50%时,rseFCM算法和SPFCM算法的聚类性能略优于IFCM(c+p)算法,对类似2D15这样的小样本数据集而言这种情况是可能的,而IFCM(c+p)算法在大规模数据集的聚类问题上可以表现出很好的效果。在本文提到的其他数据集中,IFCM(c+p)算法均能保持最好的聚类性能。在高维大样本的手写数字集MNIST和大样本的forest数据集的实验结果中可以发现IFCM(c+p)算法在提高了聚类性能的同时还具备很好的稳定鲁棒性,这是本文其他算法不具备的。另外还可以发现随着数据块大小的增加,所有增量式模糊聚类算法的聚类性能均呈下降趋势,这是由于本文提及的增量式算法均采用分块处理的方式,随着数据块大小的增加直至接近原数据集大小时,在某数据块中聚类就相当于在整个数据集上进行聚类,很明显这样增加算法运行时间的同时还降低了聚类性能。另外还注意到对于大样本数据,随机抽取的数据块较小时rseFCM算法会由于无法加载进内存而致使该算法失效,而IFCM(c+p)算法不用担心这个问题。
2)各算法在数据集上运行时间的加速比比较
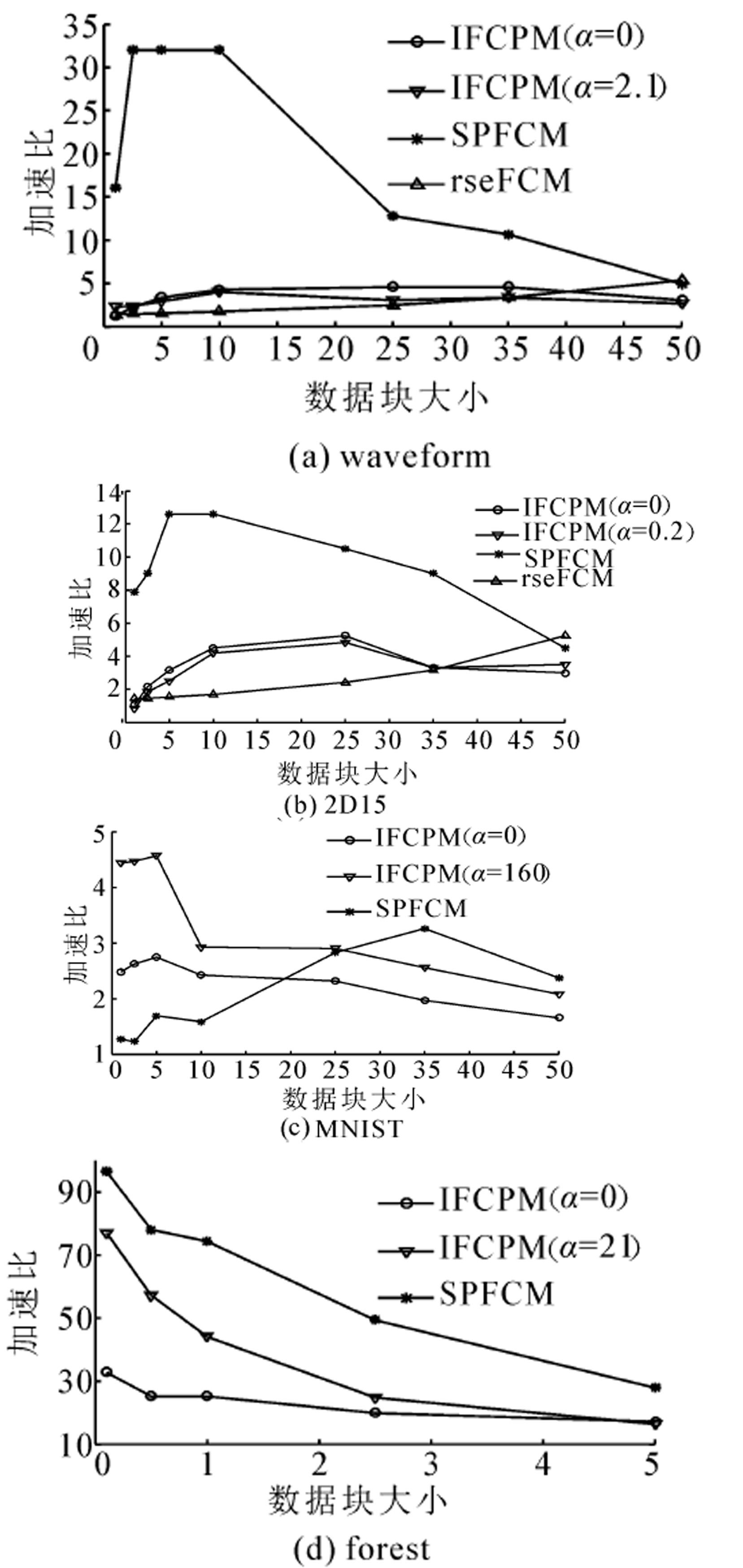
各个算法相对于FCPM算法在不同数据集上不同大小的数据块下运行时间的加速比的比较情况下图1所示。
|
| 图 1 IFCM(c+p)、SPFCM、rseFCM算法在不同数据集的不同大小数据块下的加速比 Fig. 1 Speedup ratio of IFCM(c+p),SPFCM,rseFCM for different chunk size of different datasets |
从图1中可以看出,本文提到的算法的运行时间的加速比基本上随着数据块大小的增加呈下降趋势,这是由于随着数据块大小的增加,提到的算法单次运行的样本总量在增加,因而运行时间会随之增加。在小样本数据集waveform和2D15中,IFCM(c+p)算法的运行时间高于SPFCM算法。由于forest数据集的数据块取得较小,因而SPFCM算法在此时的运行时间也较短。而在大样本的MNIST数据集中,SPFCM算法的加速程度明显降低,IFCM(c+p)算法的加速程度明显提高。由此可见,IFCM(c+p)算法会随着数据集样本的增加而加速程度得到提高,尤其是对于一类聚类中心已知的大规模数据集,该算法的运行时间会大幅降低。
4 结束语针对FCPM算法对大样本数据聚类性能较差甚至可能出现算法失效的问题,本文在该算法的基础上提出了IFCM(c+p)算法,特别是适合处理某一类已知的大规模数据集的聚类问题。通过对每一个数据块使用FCPM算法获取其聚类中心,并把它们及其附近的一些样本点加入到下一个数据块中参与聚类,同时添加平衡项以提高聚类性能。通过第3部分的实验可以发现,平衡项的加入提高了IFCM(c+p)算法的聚类性能和运行时间,另外还保持了很好的稳定鲁棒性。平衡项中的平衡因子的合理选择是IFCM(c+p)算法的关键所在,本文中所采用的方法是根据经验值,保证公式(7)中的J(U,T,V)值与平衡项尽量处于同一数量级,取在各数据集下IFCM(c+p)算法能够达到最好的聚能性能时的α值作为算法的最佳平衡因子。对于如何才能选取更好的平衡因子α,如何既保证算法的聚类性能又提高运行时间,都是我们继续研究的方向。
| [1] | BEZDEK J C, EHRLICH R, FULL W. FCM: the fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2): 191-203. |
| [2] | CAN F, DROCHAK N D II. Incremental clustering for dynamic document databases[C]//Proceedings of the 1990 Symposium on Applied Computing. Fayetteville, AR, USA, 1990: 61-67. |
| [3] | KAUFMAN L, ROUSSEEUW P J. Finding groups in data: an introduction to cluster analysis[M]. New York: John Wiley & Sons, 2009: 830-832. |
| [4] | GUHA S, RASTOGI R, SHIM K. Cure: an efficient clustering algorithm for large databases[J]. Information systems, 2001, 26(1): 35-58. |
| [5] | CAN F. Incremental clustering for dynamic information processing[J]. ACM transactions on information systems, 1993, 11(2): 143-164. |
| [6] | CAN F, FOX E A, SNAVELY C D, et al. Incremental clustering for very large document databases: Initial MARIAN experience[J]. Information sciences, 1995, 84(1/2): 101-114. |
| [7] | ZHANG Tian, RAMAKIRSHNAN R, LIVNY M. BIRCH: An efficient data clustering method for very large databases[C]//Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data. New York, USA, 1996: 103-114. |
| [8] | NG R T, HAN Jiawei. CLARANS: A method for clustering objects for spatial data mining[J]. IEEE transactions on knowledge and data engineering, 2002, 14(5): 1003-1016. |
| [9] | SHANKER B U, PAL N R. FFCM: An effective approach for large data sets[C]//Proceedings of the 3rd International Conference on Fuzzy Logic, Neural Nets and Soft Computing. Iizuka, Japan, 1994: 331-332. |
| [10] | CHENG Taiwai, GOLDGOF D B, HALL L O. Fast clustering with application to fuzzy rule generation[C]//Proceedings of 1995 IEEE International Fuzzy Systems, 1995. International Joint Conference of the Fourth IEEE International Conference on Fuzzy Systems and The Second International Fuzzy Engineering Symposium. Yokohama, Japan, 1995: 2289-2295. |
| [11] | KOLEN J F, HUTCHESON T. Reducing the time complexity of the fuzzy c-means algorithm[J]. IEEE transactions on fuzzy systems, 2002, 10(2): 263-267. |
| [12] | KOTHARI D, NARAYANAN S T, DEVI K K. Extended fuzzy c-means with random sampling techniques for clustering large data[J]. International journal of innovative research in advanced engineering (IJIRAE), 2014, 1(1): 1-4. |
| [13] | HORE P, HALL L O, GOLDGOF D B. Single pass fuzzy c means[C]//Proceedings of IEEE International Fuzzy Systems Conference. London, UK, 2007: 1-7. |
| [14] | HORE P, HALL L O, GOLDGOF D B, et al. Online fuzzy c means[C]//Proceedings of Annual Meeting of the North American Fuzzy Information Processing Society. New York, USA, 2008: 1-5. |
| [15] | HAVENS T, BEZDEK J, LECKIE C, et al. Fuzzy c-means algorithms for very large data[J]. IEEE transactions on fuzzy systems, 2012, 20(6): 1130-1146. |
| [16] | WANG Yangtao, CHEN Lihui, MEI Jianping. Incremental fuzzy clustering with multiple medoids for large data[J]. IEEE transactions on fuzzy systems, 2014, 22(6): 1557-1568 |
| [17] | B�ZHM C, PLANT C, SHAO J, et al. Clustering by synchronization[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA, 2010: 583-592. |
| [18] | 应文豪, 许敏, 王士同, 等. 在大规模数据集上进行快速自适应同步聚类[J]. 计算机研究与发展, 2014, 51(4): 707-720. YING Wenhao, XU Min, WANG Shitong, et al. Fast adaptive clustering by synchronization on large scale datasets[J]. Journal of computer research and development, 2014, 51(4): 707-720. |
| [19] | LESKI J M. Fuzzy (c+p) -means clustering and its application to a fuzzy rule-based classifier: towards good generalization and good interpretability[J]. IEEE transactions on fuzzy systems, 2014, 23(4): 802-812. |
| [20] | LIU Jun, MOHAMMED J, CARTER J, et al. Distance-Based clustering of CGH data[J]. Bioinformatics, 2006, 22(16): 1971-1978. |
| [21] | DENG Zhaohong, CHOI K S, CHUNG Fulai, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]. Pattern recognition, 2010, 43(3): 767-781. |
| [22] | RAND W M. Objective criteria for the evaluation of clustering methods[J]. Journal of the American statistical association, 1971, 66(336): 846-850. |



