仿人机器人是研究人类智能的高级平台,它是集机械、电子、传感技术、控制、人工智能、仿生学等多学科的复杂智能系统。在近50 年的发展历程中,仿人机器人技术取得了飞速的发展,已成为机器人领域的重要研究方向之一。Nao机器人是Aldebaran Robotics公司开发的一款可编程类人机器人,在研究领域得到世界范围的广泛应用,不仅应用于机器人研究、人工智能、工程学和计算机科学领域,还运用在社会学和医疗保健领域,其研究项目包括语音识别、视频处理、模式识别、自闭症治疗、多智能体系统、路径规划等。是否具备学习的能力是机器人智能性的重要体现,而模仿学习[1]作为机器人学习的重要方式,为避开繁琐困难的底层运动控制实现复杂运动的生成提供了可能,在机器人仿生学中占有重要地位。
所谓模仿学习是指模仿者(机器人)通过“观察”示教者(人或机器人)的运动行为,学习运动控制策略,泛化输出,进而获取运动技能[2]。模仿学习的过程可分为3个过程:行为感知、行为表征、行为再现,分别对应示教数据获取,特征编码进行表征学习和泛化输出的过程。示教数据的获取通过体态感知来实现,体态感知作为一种自然的人机交互方式,以其传达意图的便捷性和丰富性,能够有效实现人机对话,在智能识别与控制系统中应用广泛,常见的体感设备有惯性穿戴式系统,如3DSuit、数据手套等,光学式动作捕捉系统,如微软的Kinect体感摄影机等。表征学习是对示教数据的特征进行编码,基于概率模型的轨迹水平表征是将运动建模为随机模型,如高斯混合模型(GMM)[3, 4, 5]、隐马尔可夫模型(HMM)[6]等,具有较强的编码和噪声处理能力,抗干扰性强,能够处理高维问题。行为再现包括运动轨迹再现和运动控制再现,轨迹再现是将编码的数据通过回归技术,如高斯过程回归(GPR)[7]、高斯混合回归(GMR)[8]等,得到泛化输出的过程,控制再现是将泛化的输出映射到机器人底层运动控制中,实现动作复现,即行为动作的模仿。
机器人动作模仿系统的研究已取得一定进展,但大多是在仿真环境下的实现,见文献[9, 10];物理环境下的实现如文献[11],利用穿戴式动作捕捉系统Xsens MVN进行数据的采集,实现机器人的动作模仿,取得了良好的效果,但其数据采集所需的硬件代价较高,文献[12]能够实现基本动作的模仿,但对复杂动作的再现可靠性和稳定性不足。
本文以模仿学习的框架为指导,将体态感知与Nao机器人相结合,构建了机器人的动作模仿系统,实现了Nao机器人动作模仿学习。利用Microsoft的Kinect体感摄像机进行骨骼跟踪,获取示教者示教过程中人体节点的空间坐标信息,经预处理后得到模仿学习的示教数据;通过高斯混合模型(GMM)对示教数据进行编码表征,利用高斯混合回归(GMR)泛化输出,映射到Nao机器人中,实现动作的模仿。该系统可以实现在线和离线两种模式的动作模仿,在线模式下,可以进行实时的复杂动作模仿,运动轨迹平滑稳定;离线模式下可以通过学习多次示教泛化出最佳轨迹,具有较强的噪声处理能力,而且可以通过控制重采样点数目,实现动作执行速度的控制,更主要的是一旦学会,可以形成动作记忆,实现示教动作的重复执行。
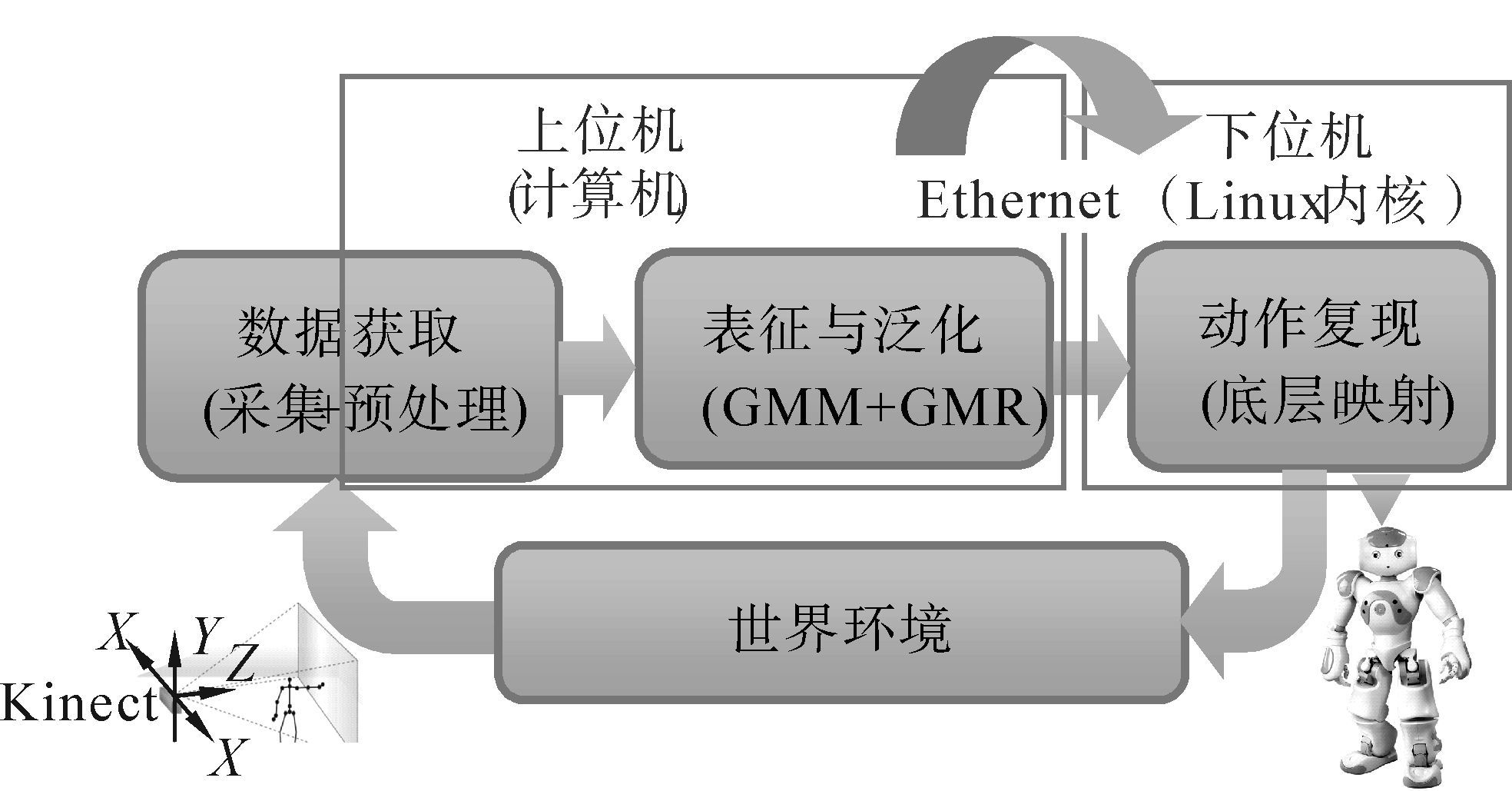
1 Nao机器人模仿学习系统构建以机器人模仿学习的框架为指导,构建了Nao机器人动作模仿的系统结构,如图1所示。利用Kinect的骨骼跟踪,采集示教者骨骼点三维空间坐标信息,经上位机预处理实现示教数据获取;通过GMM对示教数据信息进行编码,利用GMR泛化输出后,通过Ethernet(以太网)与下位机通信,映射到Nao机器人的底层运动控制中,在Nao机器人的Linux内核下进行运动控制,实现动作的模仿。
|
| 图 1 机器人动作模仿的系统结构 Fig. 1 The system structure of robot imitation |
示教动作信息的获取是机器人模仿实现的基础,系统利用Kinect采集骨骼点信息,建立虚拟坐标系,由节点信息得到各关节向量,计算向量间的夹角,进而得到各关节控制角度,即可获得各关节运动信息,为模仿的表征学习提供数据支持。
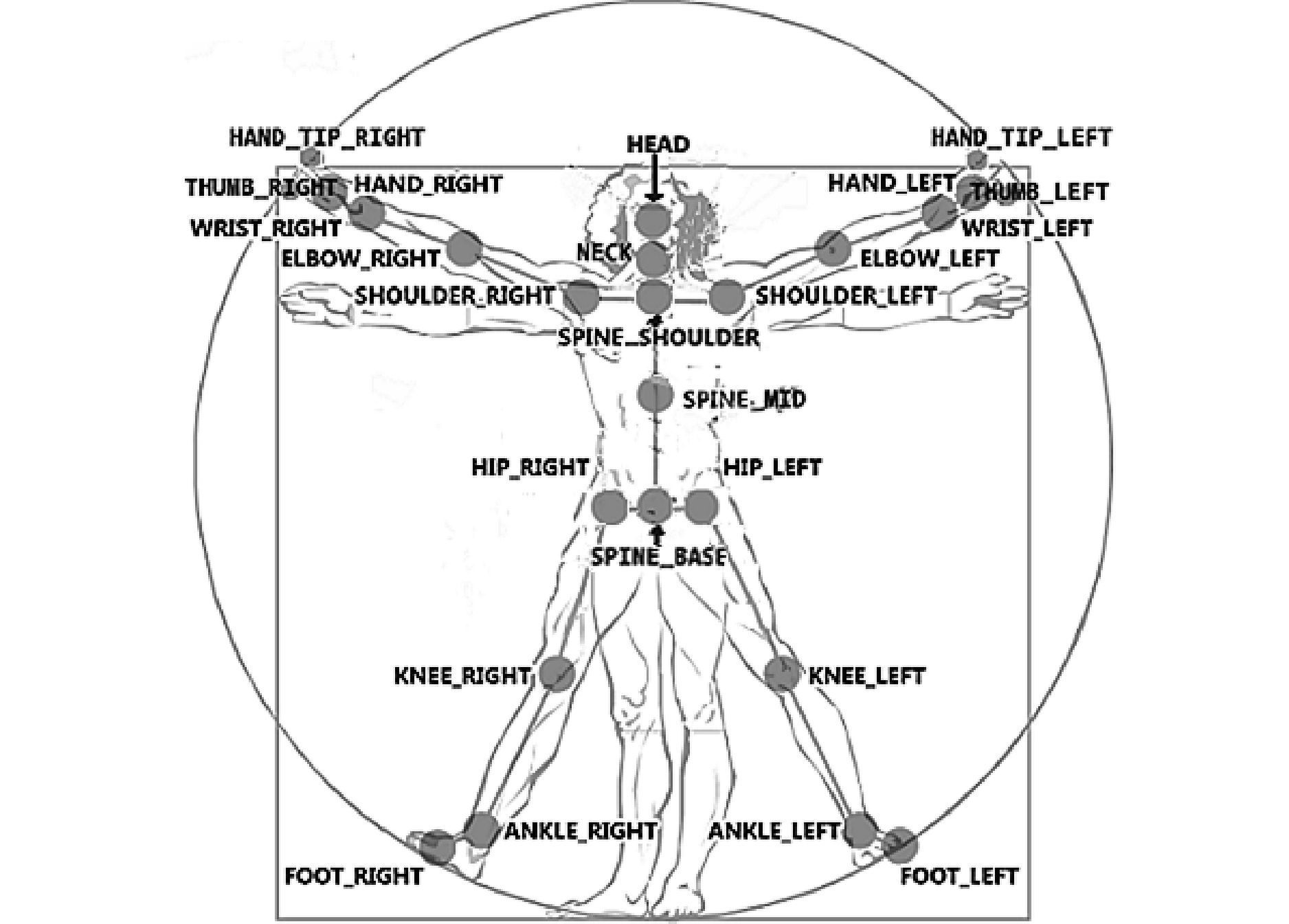
2.1 示教者骨骼点信息采集Kinect for windows v2 是微软专为开发者发布的一款3D体感摄影机,包含RGB 彩色摄像机及由红外线发射器和红外线CMOS 摄像机所构成的3D 深度传感器,利用彩色摄像头采集到的彩色图像与红外摄像头采集到的深度图像,导入即时动态捕捉、影像辨识功能,能够提取25个关节点,从而得到人体的骨架信息,S=[s1,s2,…,si,…,s25],其中si=(xi,yi,zi),如图2,Kinect的空间坐标系如图3。
|
| 图 2 Kinect提取的人体骨骼点信息 Fig. 2 Skeleton point information of human body extracted from Kinect |

|
| 图 3 Kinect的空间坐标系 Fig. 3 The space coordinate system of Kinect |
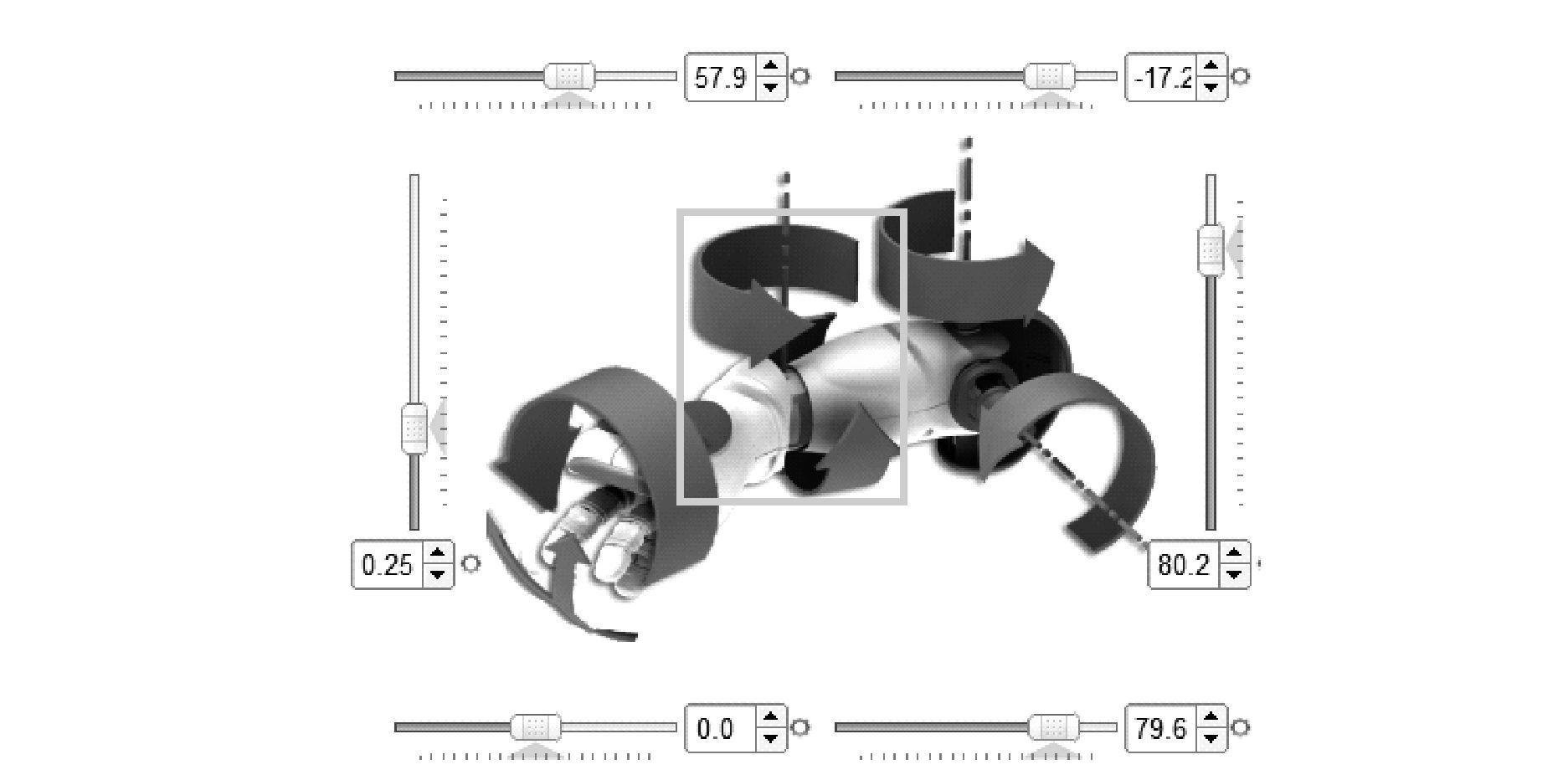
仿人机器人Nao是Aldebaran Robotics公司开发机器人平台,具有25个自由度,共13个关节,右上肢的自由度如图4所示。由于Kinect采集的骨骼信息中均认定所有关节为质点,故末端关节的转动信息无法从Kinect提取的骨架信息中计算得到,因此忽略各关节的转动信息,推导出各关节对应的自由度及所需的Kinect骨骼点如表1所示。
|
| 图 4 Nao机器人右上肢自由度 Fig. 4 The DOF of right upper limb of Nao robot |
| 关节 | 自由度 | Kinect骨骼点 |
| 头部(Head) | HeadPitch | Head、Neck、Spine_Shoulder |
| 手部(Hand) | LHand、RHand | None |
| 左肩(LShoulder) | LShoulderPitch、LShoulderRoll | Elbow_L、Shoulder_L、Spine_Shoulder、Spine_Mid |
| 右肩(RShoulder) | RShoulderPitch、RShoulderRoll | Elbow_R、Shoulder_R、Spine_Shoulder、Spine_Mid |
| 左肘(LElbow) | LElbowYaw、LElbowRoll | Wrist_L、Elbow_L、Shoulder_L、Spine_Shoulder |
| 右肘(RElbow) | RElbowYaw、RElbowRoll | Wrist_R、Elbow_R、Shoulder_R、Spine_Shoulder |
| 左大腿(LHip) | LHipPitch、LHipRoll | Knee_L、Hip_L、Spine_Base、Spine_Mid |
| 右大腿(RHip) | RHipPitch、RHipRoll | Knee_R、Hip_R、Spine_Base、Spine_Mid |
| 左膝(LKnee) | LKneePitch | Ankle_L、Knee_L、Hip_L |
| 右膝(RKnee) | RKneePitch | Ankle_R、Knee_R、Hip_R |
利用Kinect获取骨骼点三维坐标信息,生成关节向量,通过计算关节向量的夹角得到各关节控制角,以右肘翻滚角RElbowRoll和偏航角RElbowYaw(图4中方框部分)为例,对关节角的计算过程进行说明。由表1知,为求RElbowRoll和RElbowYaw的关节角需要Kinect提取的骨骼点有Wrist_R、Elbow_R、Shoulder_R,Spine_Shoulder,如图2所示,分别用p1、p2、p3、p4表示,设其三维坐标信息分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4)则有向量:
\[\left\{ \begin{align}
& {{p}_{2}}{{p}_{1}}={{p}_{1}}-{{p}_{2}}=\left( {{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}},{{z}_{1}}-{{z}_{2}} \right) \\
& {{p}_{2}}{{p}_{3}}={{p}_{3}}-{{p}_{2}}=\left( {{x}_{3}}-{{x}_{2}},{{y}_{3}}-{{y}_{2}},{{z}_{3}}-{{z}_{2}} \right) \\
& {{p}_{3}}{{p}_{4}}={{p}_{4}}-{{p}_{3}}=\left( {{x}_{4}}-{{x}_{3}},{{y}_{4}}-{{y}_{3}},{{z}_{4}}-{{z}_{3}} \right) \\
\end{align} \right.\]
(1)
$$\eqalign{
& {\theta _{RElbowRoll}} = < {p_2}{p_1},{p_2}{p_3} > = \cr
& \arccos \left( {\frac{{{p_2}{p_1} \cdot {p_2}{p_3}}}{{\left| {{p_2}{p_1}} \right|\left| {{p_2}{p_3}} \right|}}} \right) \cr} $$
(2)
记向量p3,4p2,3=p3p4×p2p3,则关节角RElbowYaw为
$$\eqalign{
& {\theta _{RElbowYaw}} = \left\langle {{p_{3,4}}{p_{2,3}},{p_2}{p_1}} \right\rangle + \frac{\pi }{2} = \cr
& \arccos \left( {\frac{{{p_{3,4}}{p_{2,3}} \cdot {p_2}{p_1}}}{{\left| {{p_{3,4}}{p_{2,3}}} \right|\left| {{p_2}{p_1}} \right|}}} \right) + \frac{\pi }{2} \cr} $$
(3)
如表1所示,共15个自由度,其中,左肘偏航角LElbowYaw的计算与RElbowYaw类似,如式(3)所示,其余各自由度的计算与RElbowRoll类似,如式(2)所示,不同之处在于根据选取向量的方向不同,参照Nao机器人的各自由度角度变化范围,作取负、加减π/2或π的校正,如此,即可得到各自由度一系列角度变化信息,也即模仿学习的示教数据。为得到平滑稳定的运动轨迹,需对离散数据进行表征学习,作进一步的泛化处理,得到连续的运动轨迹。
3 示教数据的表征与泛化将各关节角的运动信息,即示教数据,分别利用GMM进行编码,实现表征学习,通过GMR进行数据重构,泛化输出,以得到连续模仿运动轨迹[8]。
3.1 示教数据的表征与泛化
对任一自由度,设其第j个示教数据点为ξj={ξs,j,ξt,j},j={1,2,…,N},其中,N是单次示教包含的数据点的个数,ξs,j是关节角,ξt,j是时间值。假设每一个数据点ξj服从如下概率分布:
$$p\left( {{\xi _j}} \right) = \sum\limits_{k = 1}^k {p\left( k \right)p\left( {{\xi _j}\left| k \right.} \right)} $$
(4)
$$p\left( k \right) = {\pi _k}$$
(5)
$\eqalign{
& p\left( {{\xi _j}\left| k \right.} \right) = N\left( {{\xi _j};{\mu _k},{\sum _k}} \right) = \cr
& \frac{1}{{\sqrt {{{\left( {2\pi } \right)}^D}\left| {{\sum _k}} \right|} }}{e^{ - \frac{1}{2}}}^{\left( {{{\left( {{\xi _j} - {\mu _k}} \right)}^T}\sum {k^{ - 1}}\left( {{\xi _j} - {\mu _k}} \right)} \right)} \cr} $$
(6)
示教数据的ξt用作查询点,对应的空间值ξ′s利用GMR进行估计。已知p(ξj|k)满足高斯分布,即$\left( \begin{align}
& {{\xi }_{s,k}} \\
& {{\xi }_{t,k}} \\
\end{align} \right)\sim N\left( {{\mu }_{k}},{{\sum }_{k}} \right),其中,$${\mu _k} = \left\{ {{\mu _{s,k}},{\mu _{t,k}}} \right\}$$,$$\left\{ \matrix{
{\sum _{s,k}}{\sum _{st,k}} \hfill \cr
{\sum _{ts,k}}{\sum _{t,k}} \hfill \cr} \right\}$,则在给定ξt,k下,ξs,k的条件概率也满足高斯分布,即ξs,k|ξt,k~N(μ′s,k,∑′s,k)。
\[{{{\mu }'}_{s,k}}={{\mu }_{s,k}}+{{\sum }_{st,k}}{{\left( {{\sum }_{t,k}} \right)}^{-1}}\left( {{\xi }_{t,k}}-{{\mu }_{t,k}} \right)\]
(7)
\[{{{\sum }'}_{s,k}}={{\sum }_{s,k}}-{{\sum }_{st,k}}{{\left( {{\sum }_{t,k}} \right)}^{-1}}{{\sum }_{ts,k}}\]
(8)
由式(7)、(8)可得,K个高斯成分的高斯混合模型的均值μ′s和方差Σ′s。
$${\eta _k} = \frac{{p\left( {{\xi _t}\left| k \right.} \right)}}{{\sum _{i = 1}^kp\left( {{\xi _t}\left| i \right.} \right)}}$$
(9)
$${{\mu '}_s} = \sum\limits_{k = 1}^k {{\eta _k}{{\mu '}_{s,k}}} $$
(10)
$${{\sum '}_s} = \sum\limits_{k = 1}^k {\eta _k^2} {{\sum '}_{s,k}}$$
(11)
由ξs,k|ξt,k~N(μ′s,k,∑′s,k)分布估计条件期望E(ξs|ξt),即μ′s为ξt对应的重构空间值,则泛化的数据点为$\xi ' = \left\{ {{{\xi '}_s},{\xi _t}} \right\}$,该点不包含在示教数据中,但封装了示教行为的所有本质特征,在协方差约束Σ′s下能够生成平滑的运动轨迹。
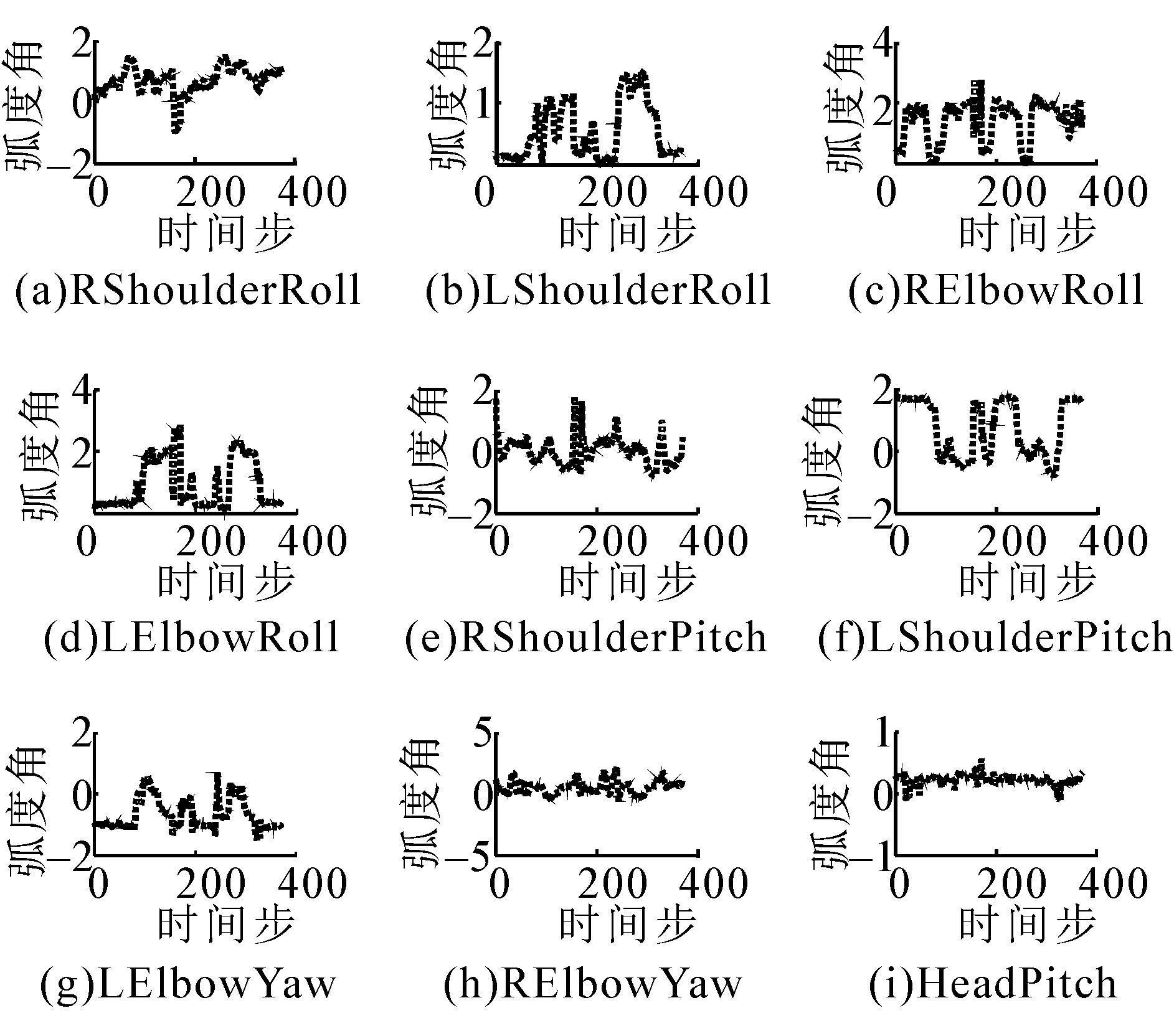
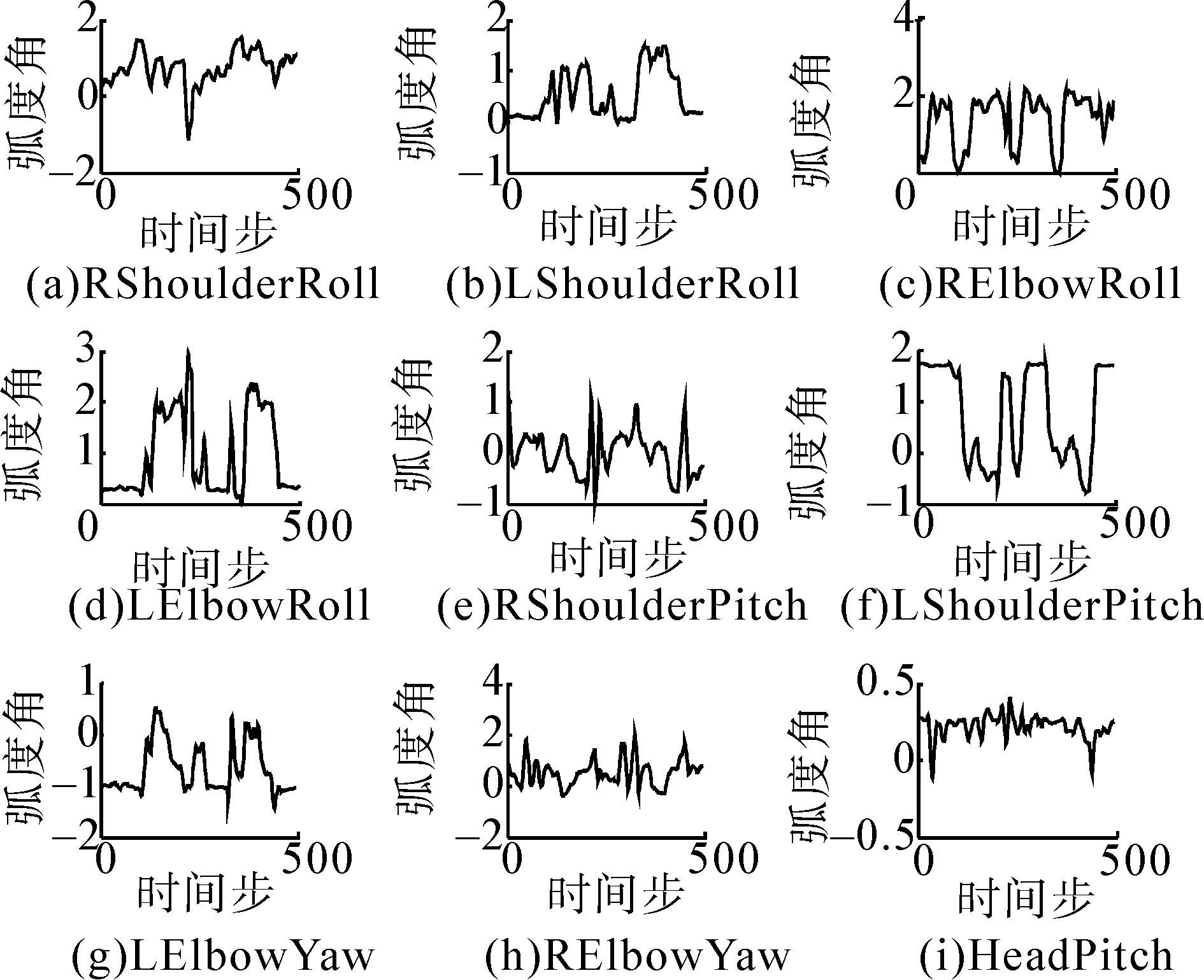
3.2 实验设计与分析示教者(人)做一套连贯的动作(包括抬臂、伸展、挥手等),经预处理后得到的上肢的9个自由度(包括双臂和头部)的角度变化信息,如图5所示。将这些数据加入到GMM进行编码,经表征学习后,利用GMR泛化输出,得到连续的运动轨迹,如图6所示,可知,经表征和泛化后,得到连续的运动轨迹,而且原始数据中的噪声得到很好的处理,波动性大大降低,稳定性增强。
|
| 图 5 示教数据的角度变化信息 Fig. 5 Angle change information of demonstration data |
|
| 图 6 经表征和泛化后的角度变化信息 Fig. 6 The angle change information of demo data after representation and generalization |
以RShoulderRoll、RElbowRoll、RShoulderPitch3个自由度为例,对单次示教的表征和泛化过程进行说明,如图7所示,每列表示一个自由度,第1行是原始数据,第2行是GMM编码的结果,第3行实线是GMR泛化的输出,阴影表示协方差约束。

|
| 图 7 单次示教的GMM编码和GMR泛化 Fig. 7 The output of single demonstration after encoding by GMM and generalization by GMR |
在离线模式下,可以对多次示教进行学习,如图8所示,是对摆臂动作进行三次示教,以RElbowRoll自由度为例进行的说明,依次对应示教数据获取、表征编码及泛化输出的过程。对原始数据处理后得到示教数据,由图可知,GMM能对多次示教进行编码,利用GMR泛化出包含多次示教特征的输出,具有较强的噪声处理能力,如果某次示教过程中存在干扰或跳变,可编码多次示教的特性可对噪声进行自动过滤,泛化出最优轨迹。
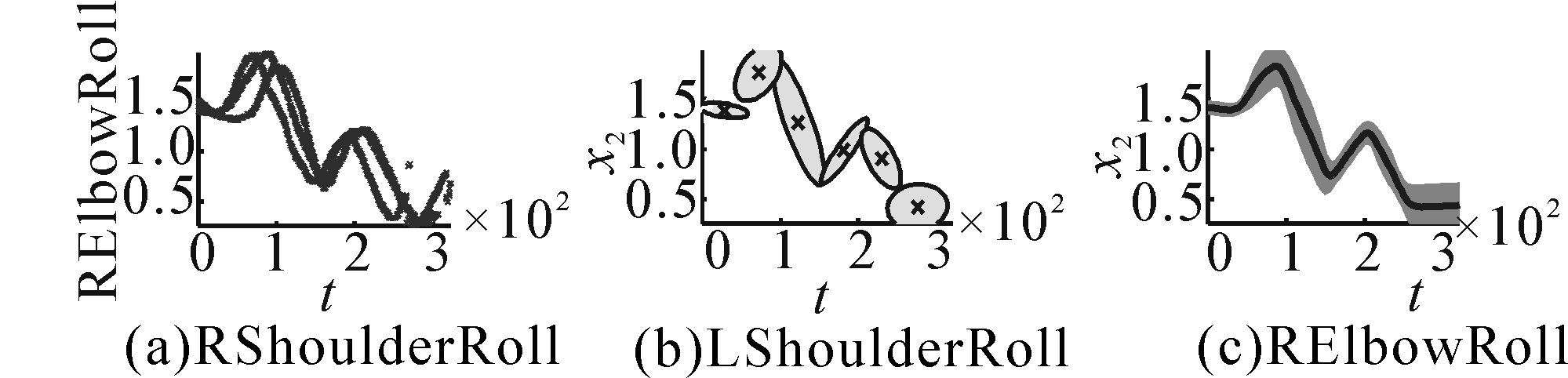
|
| 图 8 多次示教的GMM编码和GMR泛化 Fig. 8 The output of multi-demonstration after encoding by GMM and generalization by GMR |
Nao机器人的嵌入式软件NAOqi包含一个跨平台的分布式机器人框架,为开发人员提高、改进Nao的各项功能提供了一个良好的基础。本文构建的Nao机器人动作模仿系统,骨骼点信息采集及示教数据的获取采用C#语言开发实现,示教数据的表征与泛化基于MATLAB环境开发实现,将泛化得到的运动信息通过NAOqi进行数据的更新,映射到Nao机器人的底层控制中,实现动作模仿。
实验研究表明,构建的基于Kinect的Nao机器人动作模仿系统可以实现实时、离线两种方式的动作行为模仿,实时动作模仿展示如图9~12所示,对每一个子图,左边是示教者,右边是模仿者(Nao机器人),中间是计算机界面,包括Kinect采集到的人体骨骼信息和运用Nao机器人的开发套件NaoSim与Choregraphe,在虚拟环境下的动作模拟测试结果,其中,图9~11是基本动作的模仿,图9是双臂伸展动作,图10是双臂弯曲动作,图11分别表示头部自由度动作(低头)和手的状态模仿(右手闭合,左手张开),图12是复合动作,分别是挥手和武术起手式动作。

|
| 图 9 双臂伸展动作 Fig. 9 The motion of stretching arms |

|
| 图 10 双臂弯曲动作 Fig. 10 Motion of bending arms |

|
| 图 11 低头及手的状态模仿 Fig. 11 Head drop and imitation of the state of hands |

|
| 图 12 复合动作 Fig. 12 Composite actions |
基于模仿系统的灵活性和稳定性,该系统可用于实际操作任务,如图13所示,控制机器人将彩笔放入笔筒中,其中A~C是左手抓取动作,对应的细节图是a~c;D~E是将彩笔从左手交换到右手,细节对于d~e;F~H是右手将彩笔放入到右边透明笔筒中,细节对应f~h,整个过程较灵活稳定。基于模仿学习的框架,将Kinect与Nao机器人相结合实现的动作模仿系统,在上肢的动作模仿中效果较好,如图9~13所示,运动平滑稳定,能够用于执行实际任务。在线模式下,示教过程中,实时更新数据,动作的模仿是实时的。本系统还可以实现离线模式下的行为动作模仿,离线模式下,数据是在示教完成后,进行数据的更新。离线模式下,可以通过记录动作执行过程中各自由度角度的变化,实现动作学习的记忆,在环境和任务不变的情况下,实现学习到的动作(技能)重复执行,可将其应用于生产线上的重复性行为动作,通过示教-模仿的机制,可有效避免机器人底层的复杂编程。

|
| 图 13 基于实时模仿的抓-放任务的实现 Fig. 13 The implementation of catch-put task based on real-time imitation |
此外,可通过重采样不同数目的泛化输出点,实现对运动速度的控制,对于图6中的一套动作,经反复试验,采样500个数据点映射到机器人中时,运动轨迹较平滑自然,若采样200个点动作较快,而800个点,则动作较慢,更多的点则显得动作迟钝。
但是,目前该系统在下肢的动作模仿中实际效果不太理想,其原因在于下肢存在平衡问题,而该系统本质上是一开环系统,为解决下肢模仿的平衡考虑引入内部传感实现闭环的控制。
5 结论本文将体态感知与仿人机器人相结合,研究机器人的模仿学习,并以该框架为指导,开发实现了基于Kinect的Nao机器人动作模仿系统。该系统在Nao机器人上肢的动作模仿中效果较好,运动平滑而自然,实验结果表明:
1) 通过Kinect采集骨骼点空间坐标,用于计算示教者运动过程的关节角变化信息的方法是可行的,能够为模型训练提供较好的数据支持。
2) 经GMM编码和GMR泛化后,能够得到连续的平滑运动轨迹,且原始数据中的噪声得到很好的处理,波动性大大降低,稳定性较好。
3) 在上肢的动作模仿中,运动较平滑稳定,能够用于复杂运动技能的学习,能够较灵活地执行遥操作任务,对面向搜救任务的机器人研究有一定的参考意义。
4) 在离线模式下,可实现动作记忆,进而实现动作的重复执行,而且可通过重采样方法对运动速度进行控制。
5) 不足之处在于,下肢存在平衡控制的问题,不能实现上下肢的协同运动。
下一步研究的方向是考虑引入闭环控制,解决下肢的平衡问题,实现上肢和下肢的协同动作,将整个系统应用于远程遥操作任务,提高其实用性。
| [1] | SCHAAL S. Is imitation learning the route to humanoid robots?[J]. Trends in cognitive sciences, 1999, 3(6): 233-242. |
| [2] | BILLARD A, CALINON S, DILLMANN R, et al. Robot programming by demonstration[M]//SICILIANO B, KHATIB O. Springer Handbook of Robotics. Berlin Heidelberg: Springer, 2008: 1371-1394. |
| [3] | ENGLERT P, PARASCHOS A, DEISENROTH M P, et al. Probabilistic model-based imitation learning[J]. Adaptive behavior, 2013, 21(5): 388-403. |
| [4] | GRIBOVSKAYA E, KHANSARI-ZADEH S M, BILLARD A. Learning non-linear multivariate dynamics of motion in robotic manipulators[J]. The international journal of robotics research, 2011, 30(1): 80-117. |
| [5] | LEE Sang H L, SUH I H, CALINON S, et al. Autonomous framework for segmenting robot trajectories of manipulation task[J]. Autonomous robots, 2015, 38(2): 107-141. |
| [6] | ASFOUR T, AZAD P, GYARFAS F, et al. Imitation learning of dual-arm manipulation tasks in humanoid robots[J]. International journal of humanoid robotics, 2008, 5(2): 183-202. |
| [7] | 于建均, 韩春晓, 阮晓钢, 等. 基于高斯过程的机器人模仿学习研究与实现[J]. 北京工业大学学报, 2015, 41(7): 1000-1004.YU Jianjun , HAN Chunxiao , RUAN Xiaogang, et al. Robot imitation learning based on Gaussian processes[J]. Journal of Beijing university of technology, 2015, 41(7): 1000-1004. |
| [8] | CALINON S. Robot programming by demonstration: a probabilistic approach[M]. Lausanne: EPFL Press, 2009: 75-100. |
| [9] | 赵姝颖, 徐文杰, 郑雪林, 等. 基于体感的机器人展示系统研究与开发[J]. 机器人技术与应用, 2012(6): 54-57.ZHAO Shuying, XU Wenjie, ZHENG Xuelin, et al. research and development of display system of Nao humanoid robot based on posture perception[J]. Robot technique and application of robot, 2012 (6): 54-57. |
| [10] | ALMETWALLY I, MALLEM M. Real-time tele-operation and tele-walking of humanoid Robot Nao using Kinect Depth Camera[C]//Proceedings of the 10th IEEE International Conference on Networking, Sensing and Control (ICNSC). 2013 10th IEEE International Conference on Evry, France: IEEE, 2013: 463-466. |
| [11] | KOENEMANN J, BENNEWITZ M. Whole-body imitation of human motions with a Nao humanoid[C]//Proceedings of the 7th ACM/IEEE International Conference on Human-Robot Interaction (HRI).2012 7th ACM/IEEE International Conference onBoston, MA, USA: IEEE, 2012: 425-425. |
| [12] | YANG Ningjia, DUAN Feng, WEI Yudi, et al.A study of the human-robot synchronous control system based on skeletal tracking technology[C]//Proceedings of IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 2013: 2191-2196. |
| [13] | BISHOP C M. Pattern recognition and machine learning[M]. New York: Springer, 2006: 423-455. |



