随着优化问题在工程应用和理论研究上日益突出,基于群体智能理论的优化算法受到人们广泛关注。近年来,人工蜂群(artificial bee colony,ABC)算法因结构简单、参数较少和易于实现的良好特性在群体智能算法中脱颖而出[1, 2]。文献[1]中指出ABC算法与遗传算法(genetic algorithm,GA)、差分进化算法(differential evolution,DE)和粒子群优化算法(particle swarm optimization,PSO)相比较,其求解质量较好。目前,ABC算法已经在人工神经网络训练[3, 4]、组合优化[5, 6]、电力系统优化[7]等多个领域成功应用。但是,ABC算法作为一种随机优化算法,也存在收敛速度慢、易陷入局部最优的不足,与其他群体智能相比,ABC算法的探索能力很强,但开发能力不足,因此,许多学者致力于ABC算法的改进工作,主要集中在对种群初始化[8, 9]、混合算法[10, 11]和学习策略[11, 12, 13]的探索,这些研究在一定程度上都提高了ABC算法的性能,但难以同时拥有较快的收敛速度和较高的收敛精度。
为了进一步增强ABC算法的性能,本文在基本ABC算法的基础上,对种群更新策略,适应度函数以及淘汰更新函数进行改进。通过对标准函数的测试表明,改进后的算法在保持良好探索能力的同时,有效提高了其开发能力,能够以较快的速度和较高的收敛精度收敛至最优解。
1 人工蜂群算法
ABC算法是通过种群协作工作来完成寻优过程的优化算法,在ABC算法中,蜂群被分为引领蜂、跟随蜂和侦查蜂3类以协同工作。假设对于一个优化问题,其最优解在D维空间,采用ABC算法对其寻优,主要过程如下:
1)初始化种群。设置种群数量为N,其中引领蜂和跟随蜂各占一半,即N/2;设置最大迭代次数和最大不更新淘汰次数;随机产生N/2个D维的初始解{x1,x2,…,xN/2},其中xi={xi1,xi2,…,xiD},i=1,2,…,N/2,并对初始解(蜜源)进行适应度评价。随机产生初始解的公式为
xij=L+rand(0,1)×(U-L)
(1)
2)种群更新。引领蜂随机选择相邻蜜源并与其产生一个新的蜜源,比较二者蜜源质量,择优保留;跟随蜂根据由引领蜂蜜源质量信息转化的概率来选择是否对该蜜源进行邻域搜索并更新。引领蜂和跟随蜂的蜜源更新公式为
vnj=xij+R×(xij-xkj)
(2)
3)概率选择。跟随蜂根据一定概率决定是否选择对引领蜂蜜源进行邻域搜索,概率信息计算公式为
\[{P_i} = \frac{{{F_i}}}{{\sum\limits_{i = 1}^{N/2} {{F_i}} }}\]
(3)
\[{F_i} = \left\{ \begin{array}{l}
\frac{1}{{1 + {\rm{fi}}{{\rm{t}}_i}}},{\rm{fi}}{{\rm{t}}_i} \ge 0\\
1 + \left| {{\rm{fi}}{{\rm{t}}_i}} \right|,{\rm{fi}}{{\rm{t}}_i} < 0
\end{array} \right.\]
(4)
4)种群淘汰。如果某个解经过一定次数的更新后,其解的质量仍未得到改善,一般认为该解陷入局部最优,此时,引领蜂将转化为侦查蜂,由式(1)重新产生一个新的解。
2 改进的人工蜂群算法 2.1 基于信息反馈的种群更新
在基本ABC算法中,种群更新是通过随机选择一个个体中的某个随机分量进行更新,主要包括选择过程和更新过程。
选择过程包括种群个体的选择和个体分量的选择,在基本算法中,二者皆采用随机选择策略,前者的随机选择有利于保持种群个体的公平竞争,但后者的随机选择却不利于个体的进化,原因在于即便一个个体分量的更新对该个体产生了积极的影响,在下一次迭代更新过程中,也不一定能够继续对该分量进行深度搜索以获得更优个体,相反,对产生消极影响的个体分量却在下次迭代中仍存在继续更新的可能,这样不仅降低了算法收敛速度,而且不利于提高解的精度。针对这一问题,本文引入个体分量记忆机制对个体信息进行反馈,使对个体进化产生积极影响的个体分量得以充分搜索,改进后算法的个体分量由随机选择变成根据前一次个体更新情况的反馈信息选择。具体做法是在前一次个体分量更新后,采用个体分量记录器CH记录其蜜源质量是否得到提高并进行反馈,如提高则CH=1,在下次迭代时仍对该个体分量进行邻域搜索;否则CH=0,随机选择一个分量进行搜索。
更新过程主要取决于更新公式,基本ABC算法中的更新公式虽有效提高了算法的探索能力,但却降低了算法的开发能力。本文基于信息反馈的思想,参考文献[14],采用最优个体引导机制对基本更新公式进行改进,即将前一次迭代产生的最优个体信息反馈到下一次迭代时个体分量的更新公式中,从而提高算法的开发能力。改进后的更新公式为
xpq=xkq+φ×(xqbest-xkq)
(5)
2.2 基于对数的适应度函数
在基本ABC算法中,概率选择过程是跟随蜂通过概率信息选择较优蜜源进行深度搜索来推动整个种群进化,概率信息反映了蜜源质量(适应度值)的好坏程度,因此,这一信息的获取在该过程中尤为重要。基本算法中的概率信息通过式(3)和(4)计算而来,但对于式(4)而言,当同时存在适应度值无限接近于零但并不相同时,所有适应度值都将趋于1,此时,选择概率也将相同,如式(6)所示。
$\left\{ \matrix{
{\rm{fi}}{{\rm{t}}_1} = 1 \times {10^{ - 20}}\buildrel {{f_4}} \over
\longrightarrow {F_1} \approx 1\buildrel {{f_3}} \over
\longrightarrow {P_1} = 0.33 \hfill \cr
{\rm{fi}}{{\rm{t}}_2} = 1 \times {10^{ - 50}}\buildrel {{f_4}} \over
\longrightarrow {F_2} \approx 1\buildrel {{f_3}} \over
\longrightarrow {P_2} = 0.33 \hfill \cr
{\rm{fi}}{{\rm{t}}_3} = 1 \times {10^{ - 100}}\buildrel {{f_4}} \over
\longrightarrow {F_3} \approx 1\buildrel {{f_3}} \over
\longrightarrow {P_3} = 0.33 \hfill \cr} \right.$
(6)
针对这一问题,本文采用基于对数的适应度函数进行改进,通过对数效应增大不同个体适应度值差异,进而区分不同个体被选择的概率,使得优秀个体更易被选择更新,而不良个体被选择的概率降低。具体做法是在最优个体适应度值达到一定精度后,采用改进的适应度函数对所有个体的解重新评价,改进后的适应度函数公式为
\[{F_i} = \frac{{0.1}}{{0.1 + \frac{1}{{\left| {{\rm{lgfi}}{{\rm{t}}_i}} \right|}}}},0 \le {\rm{fi}}{{\rm{t}}_i} \le {10^{ - \alpha }}\]
(7)
$\left\{ \matrix{
{\rm{fi}}{{\rm{t}}_1} = 1 \times {10^{ - 20}}\buildrel {{f_7}} \over
\longrightarrow {F_1} \approx 0.67\buildrel {{f_3}} \over
\longrightarrow {P_1} = 0.27 \hfill \cr
{\rm{fi}}{{\rm{t}}_2} = 1 \times {10^{ - 50}}\buildrel {{f_7}} \over
\longrightarrow {F_2} \approx 0.83\buildrel {{f_3}} \over
\longrightarrow {P_2} = 0.35 \hfill \cr
{\rm{fi}}{{\rm{t}}_3} = 1 \times {10^{ - 100}}\buildrel {{f_7}} \over
\longrightarrow {F_3} \approx 0.91\buildrel {{f_3}} \over
\longrightarrow {P_3} = 0.38 \hfill \cr} \right.$
(8)
2.3 基于最优引导的淘汰更新函数
在种群淘汰过程中,当满足种群淘汰条件时,基本算法通过式(1)重新产生新的个体,在种群进化后期不仅容易引入不良个体,误导种群进化,而且对淘汰个体的完全否定,会导致种群多样性降低。为解决这一问题,本文在满足种群淘汰条件时,采用淘汰蜜源与最优蜜源交叉引导产生新个体,这样不仅可以避免不良个体的引入,防止对种群进化产生误导,而且有利于保持种群多样性,其交叉公式为
xnm=xmbest+φ×(xmbest-xlm)
(9)
改进后算法的流程图如图 1所示。
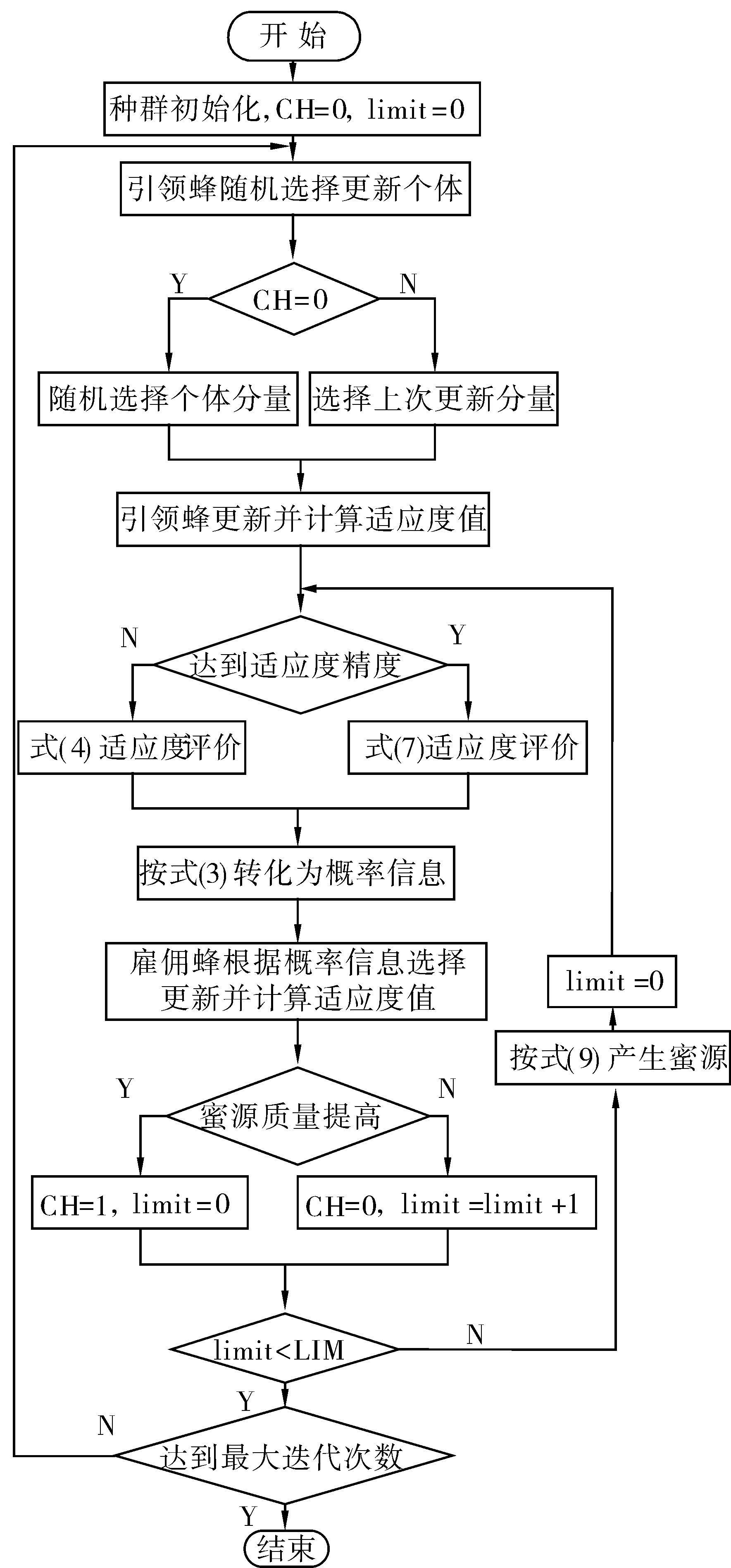 |
| 图 1 改进后算法流程图Fig. 1 The flow diagram of improved algorithm |
为验证本文所改进的ABC算法(memorial and modified ABC,MMABC)的性能,对10种基本函数进行测试。表 1列出了10种基本测试函数的名称、公式、搜索范围和理论最优值。
将MMABC与基本ABC进行比较,其中,设置参数N=50,LIM=D×N/2,测试函数维数为50和100,50维的最大迭代次数为5×104,α=8,100维的最大迭代次数为1×105,α=4。将测试函数分别采用这2种算法在MATLAB上独立运行30次,表 2为测试结果,其中Best表示最好值,Mean表示平均值,Worst表示最差值,Std表示标准差。
| Function | 函数 | 公式 | 搜索范围 | 最优值 |
| f1 | Sphere | f(x)=$\sum\limits_{i = 1}^n {X_i^2} $ | [-100,100] | 0 |
| f2 | Schwefel2.22 | f(x)=$\sum\limits_{i = 1}^n {\left| {{x_i}} \right| + \prod\limits_{i = 1}^n {\left| {{x_i}} \right|} } $ | [-10,100] | 0 |
| f3 | Schwefel2.21 | f(x)=maxi=1n|xi| | [-100,100] | 0 |
| f4 | Rosenbrock | f(x)=$\sum\limits_{i = 1}^{n - 1} {\left[ {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {1 - {x_i}} \right)}^2}} \right]} $ | [-30,30] | 0 |
| f5 | Step | f(x)=$\sum\limits_{i = 1}^n {{{\left( {\left\lfloor {{x_i} + 0.5} \right\rfloor } \right)}^2}} $ | [-100,100] | 0 |
| f6 | Quartic | f(x)=$\sum\limits_{i = 1}^n {ix_i^4 + {\rm{random}}\left[ {0,1} \right)} $ | [-1.28,1.28] | 0 |
| f7 | Schwefel2.26 | f(x)=$ - \sum\limits_{i = 1}^n {\left( {{x_i}\sin \sqrt {\left| {{x_i}} \right|} } \right)} $ | [-500,500] | -418.98n |
| f8 | Rastrigin | f(x)=$\sum\limits_{i = 1}^n {\left[ {x_i^2 - 10\cos \left( {2\pi {x_i}} \right) + 10} \right]} $ | [-5.12,5.12] | 0 |
| f9 | Ackley | f(x)=$ - 20\exp \left( { - 0.2\sqrt {\sum\limits_{i = 1}^n {x_i^2/n} } } \right) - \exp \left( {\sum\limits_{i = 1}^n {\cos \left( {2\pi {x_i}} \right)/n} } \right) + 20 + e$ | [-32,32] | 0 |
| f10 | Griewank | f(x)=${1 \over {4000}}\sum\limits_{i = 1}^n {x_i^2} - \prod\limits_{i = 1}^n {\cos \left( {{{{x_i}} \over {\sqrt i }}} \right) + 1} $ | [-600,600] | 0 |
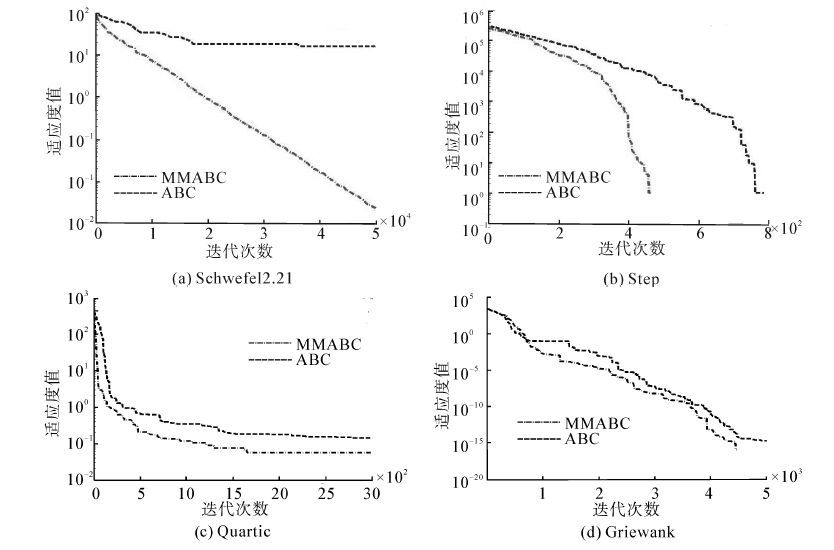 |
| 图 2 MMABC和ABC对部分测试函数收敛曲线Fig. 2 Some convergence curves of testing functions between MMABC and ABC |
| Function | Dimensions | Algorithm | Best | Worst | Mean | Std |
| f1 |
50
100 |
ABC
MMABC ABC MMABC |
8.91×10-16
0 2.09×10-15 0 |
1.13×10-15
0 2.55×10-15 0 |
9.62×10-16
0 2.33×10-15 0 |
8.52×10-17
0 1.68×10-16 0 |
| f2 |
50
100 |
ABC
MMABC ABC MMABC |
2.28×10-15
7.95×10-255 4.99×10-15 8.59×10-254 |
2.52×10-15
9.85×10-253 5.42×10-15 6.57×10-252 |
2.42×10-15
2.12×10-253 5.19×10-15 1.64×10-252 |
1.01×10-17
7.95×10-255 1.37×10-16 2.51×10-253 |
| f3 |
50
100 |
ABC
MMABC ABC MMABC |
2.85×10-2
1.35×10-16 1.14×101 1.46×10-7 |
1.39×10-1
2.22×10-15 1.33×101 5.42×10-7 |
6.58×10-2
8.89×10-16 1.21×101 2.46×10-7 |
4.12×10-2
7.32×10-16 6.64×10-1 1.49×10-7 |
| f4 |
50
100 |
ABC
MMABC ABC MMABC |
1.71×10-3
3.01×10-4 7.82×10-2 9.28×10-3 |
9.23×10-2
1.88×10-2 2.77×10-1 1.16×10-2 |
6.31×10-3
2.57×10-3 9.94×10-2 1.13×10-2 |
3.48×10-2
7.84×10-3 1.02×10-1 3.23×10-3 |
| f5 |
50
100 |
ABC
MMABC ABC MMABC |
0
0 0 0 |
0
0 0 0 |
0
0 0 0 |
0
0 0 0 |
| f6 |
50
100 |
ABC
MMABC ABC MMABC |
7.61×10-2
2.91×10-2 2.61×10-1 1.12×10-1 |
9.22×10-2
3.93×10-2 3.67×10-1 1.43×10-1 |
9.89×10-2
3.56×10-2 3.26×10-1 1.31×10-1 |
8.5×10-3
3.72×10-3 3.61×10-2 1.05×10-2 |
| f7 |
50
100 |
ABC
MMABC ABC MMABC |
-2.094 75×104
-2.094 91×104 -4.189 79×104 -4.189 83×104 |
-2.071 16×104
-2.094 91×104 -4.166 14×104 -4.189 83×104 |
-2.081 97×104
-2.094 91×104 -4.179 95×104 -4.189 83×104 |
7.57×101
3.98×10-12 8.46×101 2.64×10-3 |
| f8 |
50
100 |
ABC
MMABC ABC MMABC |
0
0 1.14×10-13 0 |
5.68×10-14
0 2.27×10-13 0 |
4.55×10-14
0 1.18×10-13 0 |
2.27×10-14
0 5.57×10-14 0 |
| f9 |
50
100 |
ABC
MMABC ABC MMABC |
1.04×10-13
1.63×10-16 1.46×10-13 2.33×10-16 |
1.47×10-13
4.44×10-16 1.61×10-13 8.87×10-16 |
1.35×10-13
3.25×10-16 1.55×10-13 5.78×10-16 |
1.59×10-14
2.35×10-17 5.32×10-15 1.42×10-17 |
| f10 |
50
100 |
ABC
MMABC ABC MMABC |
1.11×10-16
0 1.44×10-15 0 |
5.54×10-16
0 1.56×10-13 0 |
1.99×10-16
0 3.27×10-14 0 |
1.78×10-16
0 6.14×10-14 0 |
由表 2可以看出,无论测试函数是50维,还是100维,MMABC算法在解的收敛精度上与基本ABC相比有了较大提高,尤其是对测试函数f1~f3,f8~f10,一方面这是由于个体分量记忆存储机制提高了算法的开发能力,另一方面新的适应度函数能够在迭代后期增大种群个体的适应度差别,充分发挥概率选择作用,使得最终解更接近于最优解l;此外,从标准差看出MMABC算法在解的稳定性方面也表现良好。为了更加直观地观察算法的寻优过程,图 2(a)~(d)给出了部分基准函数(D=100)的收敛曲线。
为了进一步验证MMABC算法的性能,将其与文献[14]中的MABC、文献[15]中的IABC和文献[16]中的LRABC进行比较,基本参数N=50,D=30,LIM=DN/2,MMABC中α=8,MABC、IABC和LRABC中的其他参数设置分别参考文献[14, 15, 16]。表 3中给出了10种基准函数的测试结果,图中适应度值取实验平均值。
| Function | Iter | ABC | MABC | IABC | LRABC | MMABC | |
| f1 | 1×105 |
Mean
Std |
4.73×10-16
4.38×10-17 |
0
0 |
0
0 |
0
0 |
0
0 |
| f2 | 1×105 |
Mean
Std |
1.17×10-15
2.53×10-17 |
0
0 |
0
0 |
0
0 |
0
0 |
| f3 | 1×104 |
Mean
Std |
6.71×10-3
8.37×10-4 |
1.43×10-2
5.48×10-3 |
3.08×10-5
3.16×10-5 |
3.07×10-4
3.11×10-4 |
5.16×10-6
2.65×10-6 |
| f4 | 1×105 |
Mean
Std |
3.11×10-1
3.23×10-1 |
1.18×10-1
1.26×10-2 |
1.76×10-2
2.16×10-2 |
1.71×10-2
1.65×10-2 |
2.89×10-3
5.73×10-3 |
| f5 | 1×103 |
Mean
Std |
0
0 |
0
0 |
0
0 |
0
0 |
0
0 |
| f6 | 1×104 |
Mean
Std |
2.51×10-2
3.87×10-2 |
3.36×10-2
8.08×10-3 |
1.05×10-2
2.59×10-3 |
5.98×10-4
2.88×10-4 |
4.41×10-3
1.23×10-3 |
| f7 | 3×103 |
Mean
Std |
-12 569.5
1.03×10-4 |
-12 569.5
1.63×10-12 |
-12 569.5
1.15×10-12 |
-12 569.5
8.13×10-13 |
-12 569.5
3.68×10-13 |
| f8 | 3×103 |
Mean
Std |
3.41×10-14
2.78×10-14 |
0
0 |
0
0 |
0
0 |
0
0 |
| f9 | 3×103 |
Mean
Std |
9.45×10-14
8.26×10-15 |
3.92×10-14
5.22×10-15 |
3.14×10-14
2.84×10-15 |
2.31×10-15
1.74×10-15 |
1.45×10-14
1.02×10-15 |
| f10 | 3×103 |
Mean
Std |
4.44×10-17
5.43×10-17 |
0
0 |
0
0 |
0
0 |
0
0 |
由表 3可以看出,无论是MABC、IABC,还是LRABC、MMABC,在对基本ABC算法进行改进后,性能都有了一定的提高。但由测试结果还可以看出,仅有函数f6和f9,MMABC性能略差于LRABC,但其比另两种算法性能要好;对于函数f3、f4和f7测试表明,MMABC算法相比于其他3种算法不仅在收敛精度上有了提高,而且其稳定性也得以改善,尤其是对函数f3和f4。
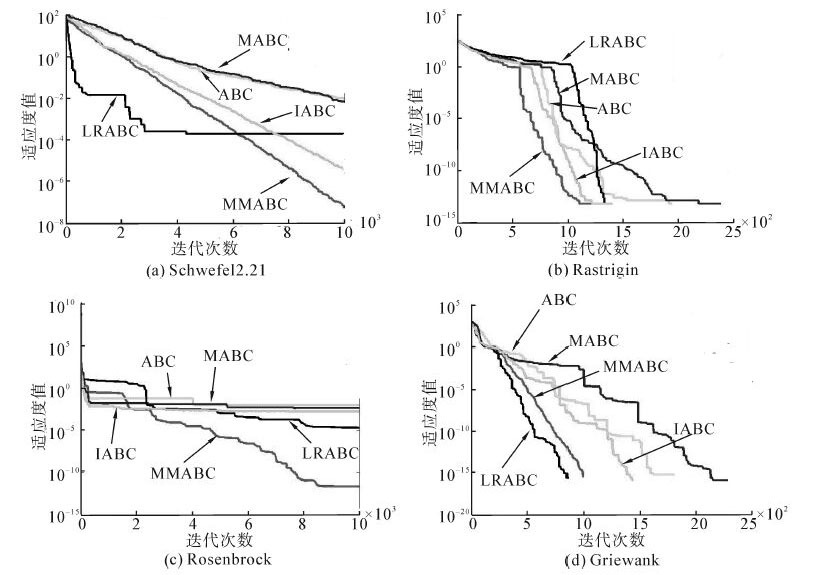 |
| 图 3 5种算法对部分函数测试对比曲线Fig. 3 Some comparison curves of testing functions between five algorithms |
为更加直观比较MMABC和其他3种改进算法以及基本ABC的性能,图 3(a)~(d)给出了这5种算法对部分函数测试结果的收敛曲线,其中(a)和(b)为单峰函数,(c)和(d)为多峰函数,图中适应度值取30次试验最优值。
从图 3中可知,对Schewefel2.21的测试结果表明,虽然LRABC算法在前期收敛速度相比于其他几种算法要快,但很快陷入局部最优,相反,MMABC算法的收敛精度较另外几种算法要高,且收敛速度仅比LRABC慢;在Rosenbrock函数的测试过程中,MMABC算法不仅有较高收敛精度,而且有较快的收敛速度;而在对Rastrigin函数的测试中,尽管5种算法都能够达到理论最优值,但MMABC算法的收敛速度较其他几种算法要快;从Griewank函数的测试曲线中看出,MMABC算法的收敛曲线几乎呈线性下降,这表明MMABC不易陷入局部最优,在收敛精度方面,5种算法都能够达到理论最优值,收敛速度方面,MMABC仅比LRABC稍慢。综上所述,无论对于单峰函数,还是多峰函数,MMABC都表现出了良好的性能,不仅在收敛速度和收敛精度上有了很大改善,而且能够有效避免陷入局部最优,具有良好的寻优性能。
4 结束语
本文针对基本ABC算法存在收敛速度慢和易陷入局部最优的缺点,从多个角度对其进行改进。首先,通过增加最优个体分量记忆机制来提高算法的开发能力,加快算法收敛速度;其次,改进适应度函数以增大迭代后期种群适应度差异,有效避免陷入局部最优;最后,为了防止在淘汰过程中引入不良个体,采用最优蜜源引导机制产生新个体。对多个函数的测试表明,改进后的算法不仅提高了收敛速度和收敛精度,而且能够有效避免“早熟”现象。后续工作可针对个别函数(如f4和f9)深入研究改进策略以提高算法泛化性能,此外,还可研究将本文改进的ABC算法应用于求解实际工程优化问题。
| [1] | KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied soft computing, 2008, 8(1): 687-697. |
| [2] | 秦全德, 程适, 李丽, 等. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2): 127-135. QIN Quande, CHENG Shi, LI Li, et al. Artificial bee colony algorithm: a survey[J]. CAAI transactions on intelligent systems, 2014, 9(2): 127-135. |
| [3] | 温长吉, 王生生, 于合龙, 等. 基于改进蜂群算法优化神经网络的玉米病害图像分割[J]. 农业工程学报, 2013, 29(13): 142-149. WEN Changji, WANG Shengsheng, YU Helong, et al. Image segmentation method for maize diseases based on pulse coupled neural network with modified artificial bee algorithm[J]. Transactions of the Chinese society of agricultural engineering, 2013, 29(13): 142-149. |
| [4] | OZTURK C, KARABOGA D. Hybrid artificial bee colony algorithm for neural network training[C]//Proceedings of IEEE Congress on Evolutionary Computation. New Orleans, LA: IEEE, 2011: 84-88. |
| [5] | ZHANG Rui, SONG Shiji, WU Cheng. A hybrid artificial bee colony algorithm for the job shop scheduling problem[J]. International journal of production economics, 2013, 141(1): 167-178. |
| [6] | ZHANG Shuzhu, LEE C K M, CHOY K L, et al. Design and development of a hybrid artificial bee colony algorithm for the environmental vehicle routing problem[J]. Transportation research part D, 2014, 31: 85-89. |
| [7] | ADARYANI M R, KARAMI A. Artificial bee colony algorithm for solving multi-objective optimal power flow problem[J]. International journal of electrical power & energy systems, 2013, 53: 219-230. |
| [8] | 匡芳君, 徐蔚鸿, 金忠. 自适应Tent混沌搜索的人工蜂群算法[J]. 控制理论与应用, 2014, 31(11): 1502-1509. KUANG Fangjun, XU Weihong, JIN Zhong. Artificial bee colony algorithm based on self-adaptive Tent chaos search[J]. Control theory & applications, 2014, 31(11): 1502-1509. |
| [9] | ALIZADEGAN A, ASADY B, AHMADPOUR M. Two modified versions of artificial bee colony algorithm[J]. Applied mathematics and computation, 2013, 225: 601-609. |
| [10] | LIAO Xiang, ZHOU Jianzhong, OUYANG Shuo, et al. An adaptive chaotic artificial bee colony algorithm for short-term hydrothermal generation scheduling[J]. International journal of electrical power & energy systems, 2013, 53: 34-42. |
| [11] | GAO Weifeng, LIU Sanyang, HUANG Lingling. Enhancing artificial bee colony algorithm using more information-based search equations[J]. Information sciences, 2014, 270: 112-133. |
| [12] | 李国亮, 魏振华, 徐蕾. 分阶段搜索的改进人工蜂群算法[J]. 计算机应用, 2015, 35(4): 1057-1061. LI Guoliang, WEI Zhenhua, XU Lei. Improved artificial bee colony algorithm using phased search[J]. Journal of computer applications, 2015, 35(4): 1057-1061. |
| [13] | BABAYIGIT B, OZDEMIR R. A modified artificial bee colony algorithm for numerical function optimization[C]//Proceedings of IEEE Symposium on Computers and Communications. Cappadocia: IEEE, 2012: 245-249. |
| [14] | GAO Weifeng, LIU Sanyang. A modified artificial bee colony algorithm[J]. Computers & operations research, 2012, 39(3): 687-697. |
| [15] | 高卫峰, 刘三阳, 黄玲玲. 受启发的人工蜂群算法在全局优化问题中的应用[J]. 电子学报, 2012, 40(12): 2396-2403. GAO Weifeng, LIU Sanyang, HUANG Lingling. Inspired artificial bee colony algorithm for global optimization problem[J]. Acta electronica sinica, 2012, 40(12): 2396-2403. |
| [16] | 刘三阳, 张平, 朱明敏. 基于局部搜索的人工蜂群算法[J]. 控制与决策, 2014, 29(1): 123-128. LIU Sanyang, ZHANG Ping, ZHU Mingmin. Artificial bee colony algorithm based on local search[J]. Control and decision, 2014, 29(1): 123-128. |



