2. 首都经济贸易大学 信息学院,北京 100070;
3. 首都经济贸易大学 计算交通科学研究中心,北京 100070;
4. 清华大学 信息技术研究院,北京 100084;
5. 北京工业大学 电子信息与控制工程学院,北京 100124
2. Information College, Capital University of Economics and Business, Beijing 100070, China;
3. Computational Transportation Science Center, Capital University of Economics and Business, Beijing 100070, China;
4. Research Institute of Information Technology, Tsinghua University, Beijing 100084, China;
5. School of Computer Science, Beijing Information Science & Technology University, Beijing 100124, China
2015年,谷歌公司研究人员在“Nature”杂志发表了一篇关于将人工智能方法应用于49个不同的游戏控制系统的研究报告[1],报告中展示了在这49个智能系统中,计算机经过反复地学习与控制过程,不但可以学会上述系统的运行规则,还在绝大多数比赛中达到了人类的操控水平,甚至还在少数项目中超越了人类。2012年以来微软、苹果公司也相继在人工智能领域进行大量研发,Cortana、Siri等智能操控系统相继上市。上述研究成果标志着人工智能研究领域已经突破了瓶颈期,成为了前沿领域的研究热点和世界一线企业进行市场竞争的焦点。
早在1997年,作为基于推理机制人工智能系统的里程碑,IBM公司研制的基于庞大规则库推理机制深蓝计算机,输入了一百多年来优秀棋手的对局两百多万局,战胜了国际象棋世界冠军卡斯帕罗夫。而在随后的10年中,人工智能却进入了一个缓慢的发展阶段。直到2007年前后,“深度神经网络”的概念[2-3]开始受到关注,Geoffrey Hinton等[4]提出了一种在前馈神经网络中进行有效训练的算法。这一算法将网络中的每一层视为无监督的受限玻尔兹曼机,再使用有监督的反向传播算法进行调优[5]。此后,神经计算科学迎来了一个跨越式的发展阶段[6-7]。
如上所述,现有的最具代表性的人工智能方法有以下两类:1)以数理逻辑、模糊推理为代表的基于规则与推理技术的人工智能方法与技术;2)以模拟人脑生物学特征构建的神经网络为特征的神经计算方法与技术。前者的特点在于:1)整个推理过程具有严格的公式定义,推理规则(先验知识)必须十分精确地描述,推理系统才可以很好地工作;2)如果推理规则不合理,系统往往无法对推理规则进行修正;3)推理模型的机理原型是数学推理机制。后者的特点在于:1)整个推理过程和规则是在系统运行过程中根据控制目标、系统状态以及输出动态修正的,因此系统可以在先验知识不足的情况下运行;2)系统运行过程中,推理机制本身可以得到优化;3)神经网络模型的机理原型是人脑生物系统的学习与思维机制。
由于神经计算科学在原理上更加接近人脑智能的生理学原理,在对于知识学习的容量与深度方面具有无限的扩展能力,因此在更为复杂的知识系统与智能的学习及表达方面具有更广阔的发展空间。
人工智能复合(改进)经典控制(AI-CC)方法在经典控制方法的基础上采用智能算法对关键参数进行整定,相对于预测控制、自适应控制等其他类型的智能控制算法具有以下优点:1)理论研究方面可以借助大量非常成熟的经典控制理论;2)大量经典控制的实际应用案例为研究工作带来了大量的实验环境和市场价值;3)在经典控制基础上,引入预测、优化、推理等经典的人工智能算法建模的难度大幅降低,无需构建新型系统模型。常见的AI-CC方法有:专家复合经典控制(E-PID)[8]、模糊复合经典控制(F-PID)[9-10]、神经网络复合经典控制(NN-PID)在线整定方法[11-12]等。上述现有方法待解决的问题如下:1)系统特性有待进行理论论证,例如普适特征与稳定性等;2)很多应用对工艺有特殊要求,例如超调量;3)系统特性有待进一步提升,例如响应速度、稳态误差、抗干扰能力等。
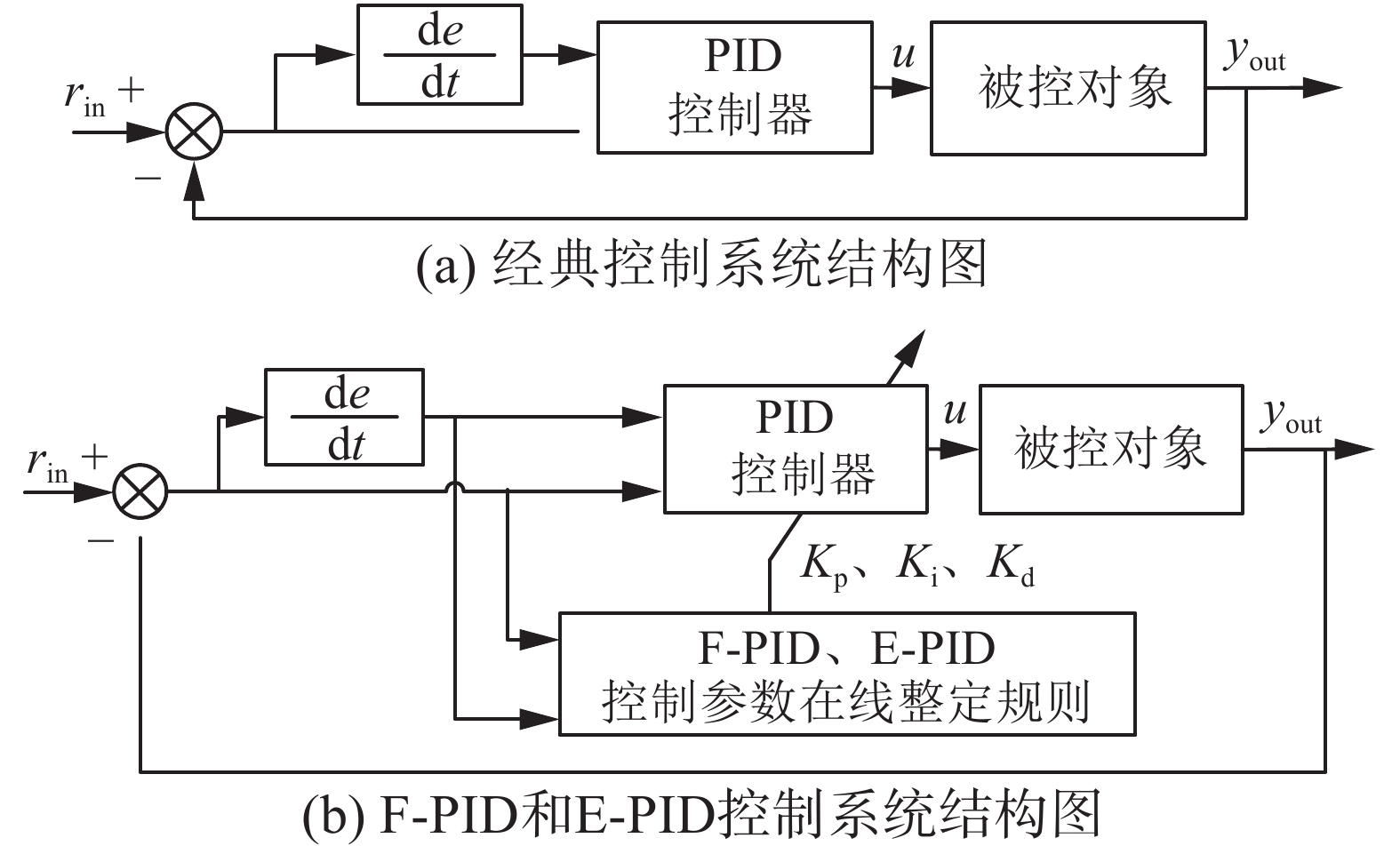
1 基于规则推理的AI-CC智能控制系统建模及改进 1.1 模型设计经典控制系统如图1(a)所示,基于规则推理与经典控制相结合的智能控制系统如图1(b)所示。如果控制参数在线整定的规则为根据系统输出及其变化率一一映射推理出控制参数,称为专家规则在线整定方法,采用E-PID表示;如果是根据系统输出及其变化率通过模糊计算出控制参数整定值,称为模糊推理在线整定方法,采用F-PID表示[13-14]。
|
图 1 现有的经典控制和智能控制方法的系统结构 Fig.1 Existing AI-CC method and system structure |
本研究在实现F-PID和E-PID的基础上,改变推理规则在线整定控制参数算法实现改进,改进的核心步骤是:E-PID和F-PID根据系统误差及变化率直接推力产生控制量,本研究提出根据系统误差及变化率产生控制量的修正量,提出EA-PID和FA-PID方法,如图2所示。

|
图 2 改进智能控制方法的系统结构图 Fig.2 Improved AI-CC method and system structure |
F-PID方法经过模糊化计算直接得到控制参数的计算公式如式(1)~(3):
| $K_{\rm{p}}\left( k \right) = R_{K_{\rm{p}}}^F(e(k),ec(k))$ | (1) |
| $K_{\rm{i}}\left( k \right) = R_{K_{\rm{i}}}^F(e(k),ec(k))$ | (2) |
| $K_{\rm{d}}\left( k \right) = R_{K_{\rm{d}}}^F(e(k),ec(k))$ | (3) |
本研究提出改进的FA-PID方法经过模糊化计算得到的结果
| $K_{\rm{p}}\left( k \right) = R_{K_{\rm{p}}}^{FA}(e(k),ec(k)) \cdot K_{\rm{p}}(k - 1)$ | (4) |
| $K_{\rm{i}}\left( k \right) = R_{K_{\rm{i}}}^{FA}(e(k),ec(k)) \cdot K_{\rm{i}}(k - 1)$ | (5) |
| $K_{\rm{d}}\left( k \right) = R_{K_{\rm{d}}}^{FA}(e(k),ec(k)) \cdot K_{\rm{d}}(k - 1)$ | (6) |
同理,E-PID方法通过查询规则表直接得到控制参数
| $K_{\rm{p}}\left( k \right) = R_{K_{\rm{p}}}^E(e(k),ec(k))$ | (7) |
| $K_{\rm{i}}\left( k \right) = R_{K_{\rm{i}}}^E(e(k),ec(k))$ | (8) |
| $K_{\rm{d}}\left( k \right) = R_{K_{\rm{d}}}^E(e(k),ec(k))$ | (9) |
本研究提出改进的EA-PID同样通过查询专家经验规则表如表1所示。
| 表 1 专家经验规则表 Tab.1 The table of expert experiences |
查询结果
| $K_{\rm{p}}\left( k \right) = R_{K_{\rm{p}}}^{EA}(e(k),ec(k)) \cdot K_{\rm{p}}(k - 1)$ | (10) |
| $K_{\rm{i}}\left( k \right) = R_{K_{\rm{i}}}^{EA}(e(k),ec(k)) \cdot K_{\rm{i}}(k - 1)$ | (11) |
| $K_{\rm{d}}\left( k \right) = R_{K_{\rm{d}}}^{EA}(e(k),ec(k)) \cdot K_{\rm{d}}(k - 1)$ | (12) |
现有的F-PID和E-PID与本研究提出改进的FA-PID和EA-PID方法对比如表2所示。
| 表 2 多种规则推理与经典控制相结合方法对比 Tab.2 Table of increase adaptive fuzzy PID ptimization rule |
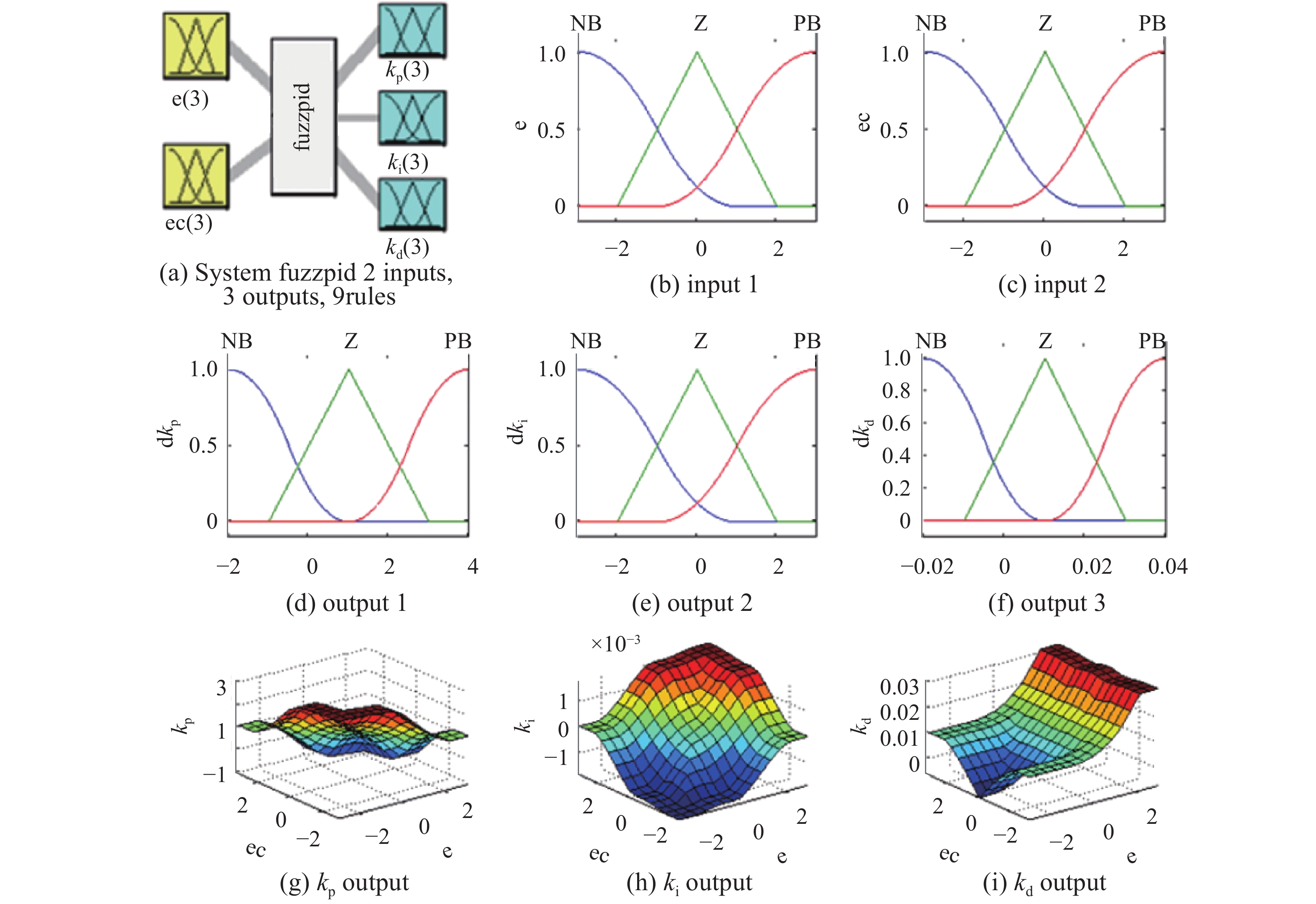
设计F-PID与FA-PID算例的模糊控制器及其关键参数分别如图3与图4所示。
|
图 3 F-PID模糊控制器参数设置 Fig.3 Parameters setting of fuzzy controller in F-PID |
若模糊规则序列
| $\mu {\rm{ = }}\frac{{\sum\nolimits_{i,j} {{\mu _i}(e) \cdot } {\mu _i}(\Delta e) \cdot {\mu _{ij}}}}{{\sum\nolimits_{i,j} {{\mu _i}(e) \cdot } {\mu _i}(\Delta e)}}$ | (13) |
设计EA-PID算法的规则表如表3所示,E-PID算法的规则表同理。
| 表 3 增量式自适应专家PID优化器规则表 Tab.3 Rule of increase expert PID optimizer |
为F-PID、FA-PID、E-PID、EA-PID智能控制系统设计相同的控制系统和实验参数:1)每个仿真周期运行一次控制参数的整定计算;2)采用增量式数字PID算法作为PID控制器算法;3)本研究采用最常见的带有延迟环节的二阶离散化模型作为被控对象模型进行研究,本研究方法可以推广到其他更多被控对象模型的情况,即
F-PID、FA-PID、E-PID、EA-PID 4中算法的仿真结果如图5所示。

|
图 4 FA-PID模糊控制器参数设置 Fig.4 Parameters setting of fuzzy controller in FA-PID |
各算法的结果指标如表4所示,实验表明:1)从系统响应的快速性角度看,基于规则表的算法快于模糊计算的算法,E-PID具有最快的起始上升速度,而EA-PID具有最快的稳定速度,FA-PID算法在上升和稳定速度方面快于F-PID算法,EA-PID算法存在超调量,其他各算法均不存在超调;2)从稳态误差的角度看,EA-PID具有最小的稳态误差,FA-PID算法在稳态误差方面低于F-PID算法;3)从抗干扰能力角度看,EA-PID算法具有最好的抗干扰能力。综上所述,EA-PID和FA-PID算法的很多控制指标都优于改进前的E-PID和FA-PID算法。
| 表 4 控制系统输出和误差的仿真结果对比 Tab.4 The comparison of simulation results of control system output and error |
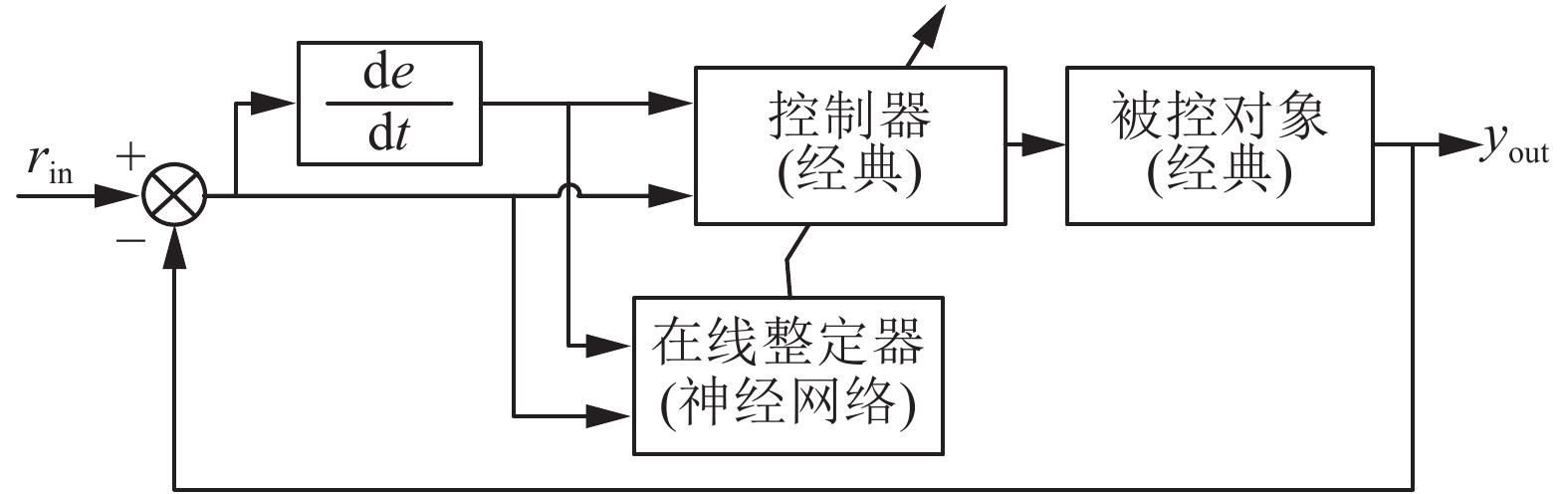
基于神经网络与经典控制相结合的智能控制方法如图6所示,神经网络输出即为更新的控制参数,从而影响经典控制器更新对被控对象的控制量。

|
图 5 各系统计算机仿真结果 Fig.5 Simulation results of each system |
令神经网络的训练目标为使系统均方误差达极小,即定义目标函数为均方误差,如式(14):
| $E(t) = \frac{1}{2}{(r_{\rm{in}}(k) - y_{\rm{out}}(k))^2}$ | (14) |
本研究提出采用改进的自适应小波神经网络[15]与经典控制相结合构成智能控制系统,即实现AWNN-PID控制,并同时实现BPNN-PID、RBFNN-PID作为对比算法[16-17],验证新方法的控制效果有所提升。
2.2 在线整定器算法令小波函数尺度变换函数
| ${\psi _{a,b}}(t) = \cos \, (1.75t) \cdot {{\rm{e}}^{ - \frac{{{t^2}}}{2}}}$ | (15) |
训练算法采用梯度下降法,对神经网络的权值
| $\Delta w_{jk}^{(3)}(t) = \alpha \cdot \Delta w_{jk}^{(3)}\left( {t - 1} \right) - \eta \cdot \frac{{\partial E(t)}}{{\partial w_{jk}^{(3)}(t)}}$ | (16) |
| $\Delta w_{ij}^{(2)}(t) = \alpha \cdot \Delta w_{ij}^{(2)}\left( {t - 1} \right) - \eta \cdot \frac{{\partial E(t)}}{{\partial w_{ij}^{(2)}(t)}}$ | (17) |
| $\Delta {a_j}(t) = \alpha \cdot \Delta {a_j}(t - 1) - \eta \cdot \frac{{\partial E(t)}}{{\partial {a_j}(t)}}$ | (18) |
| $\Delta {b_j}(t) = \alpha \cdot \Delta {b_j}(t - 1) - \eta \cdot \frac{{\partial E(t)}}{{\partial {b_j}(t)}}$ | (19) |
式中,各项的表达式如式(20)~(25):
| $\frac{{\partial E(t)}}{{\partial w_{jk}^{(3)}(t)}} \!=\! {\rm{error}}(t) \cdot {\mathop{\rm sgn}} (\frac{{\partial y(t)}}{{\partial \Delta u(t)}}) \cdot \frac{{\partial \Delta u(t)}}{{\partial o_k^{(3)}(t)}} \cdot {g'}({\rm{net}}_k^{(3)}(t)) \cdot o_j^{(2)}(t)$ | (20) |
| $\begin{aligned}\frac{{\partial E(t)}}{{\partial w_{ij}^{(2)}(t)}} = \sum\limits_{k = 1}^L {\delta _k^{(3)}} (t) \cdot w_{jk}^{(3)}(t) \cdot \\ \psi _{a,b}'\left( {\frac{{{\rm{net}}_j^{(2)}(t) - {b_j}(t)}}{{{a_j}(t)}}} \right) \cdot \frac{1}{{{a_j}(t)}} \cdot o_i^{(1)}(t)\end{aligned}$ | (21) |
| $\begin{aligned}& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \frac{{\partial E(t)}}{{\partial {a_j}(t)}} = \sum\limits_{k = 1}^L {\delta _k^{(3)}} (t) \cdot w_{jk}^{(3)}(t) \cdot \\ &\psi _{a,b}'\left( {\frac{{net_j^{(2)}(t10.) - {b_j}(t)}}{{{a_j}(t)}}} \right) \cdot \left( { - \frac{{net_j^{(2)}(t) - {b_j}(t)}}{{a_j^2(t)}}} \right)\end{aligned}$ | (22) |
| $\begin{aligned}&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \frac{{\partial E(t)}}{{\partial {a_j}(t)}} = \sum\limits_{k = 1}^L {\delta _k^{(3)}} (t) \cdot w_{jk}^{(3)}(t) \cdot \\ &\psi _{a,b}'\left( {\frac{{{\rm{net}}_j^{(2)}(t) - {b_j}(t)}}{{{a_j}(t)}}} \right) \cdot \left( { - \frac{{{\rm{net}}_j^{(2)}(t) - {b_j}(t)}}{{a_j^2(t)}}} \right)\end{aligned}$ | (23) |
| $\delta _k^{(3)}(t) = {\rm{error}}(t) \cdot {\mathop{\rm sgn}} \left( {\frac{{\partial y(t)}}{{\partial u(t)}}} \right) \cdot \frac{{\partial u(t)}}{{\partial o_k^{(3)}(t)}} \cdot {g'}\left( {\left. {{\rm{net}}_k^{(3)}(t)} \right)} \right.$ | (24) |
| $g(x) = \frac{{{{\rm{e}}^x}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}},{g'}(x) = \frac{2}{{{{({{\rm{e}}^x} + {{\rm{e}}^{ - x}})}^2}}}$ | (25) |
为BPNN-PID、RBFNN-PID、AWNN-PID仿真系统设计与F-PID、FA-PID、E-PID、EA-PID仿真系统相同的控制系统和实验参数:1)每个仿真周期运行一次控制参数的整定计算;2)采用增量式数字PID算法;3)同样采用最常见的带有延迟环节的二阶离散化模型作为被控对象模型进行研究,本方法可以推广到其他更多被控对象模型的情况,即
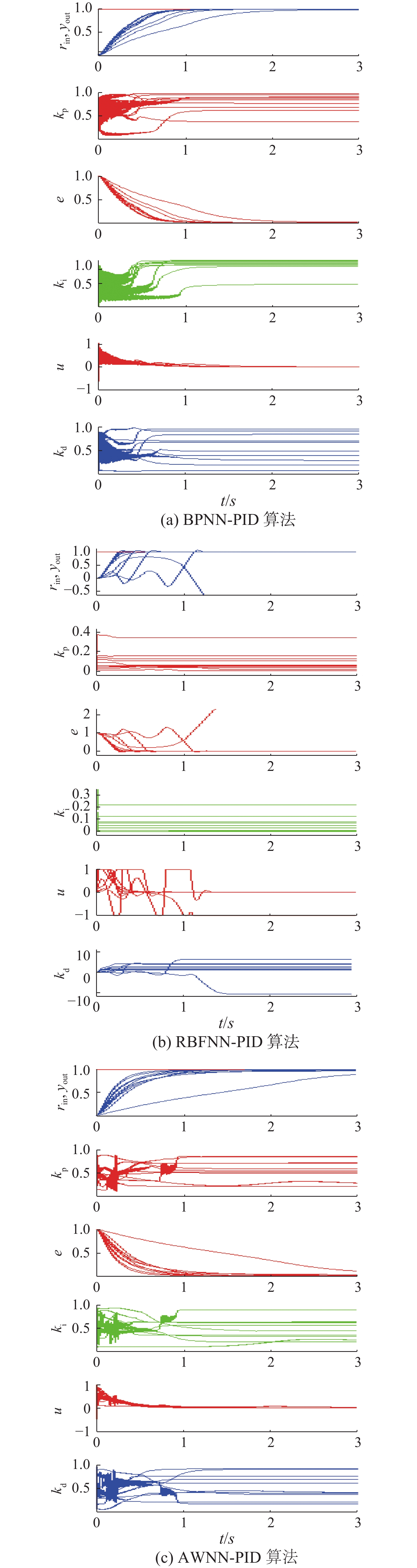
BPNN-PID、RBFNN-PID和AWNN-PID 3种算法各连续10次计算机仿真的结果如图7所示。
|
图 6 神经网络智能控制系统的结构图 Fig.6 System diagram of neural network intelligent control system |
BPNN-PID、RBFNN-PID和AWNN-PID 3种算法各连续30次计算机仿真的结果如表5所示。
| 表 5 每种算法各30次计算机仿真结果的上升时间、稳定时间、静态误差统计 Tab.5 Rise time, settling time, steady-state error statistics of 30 simulations per method |
实验表明:1)从算法可行性角度看,各算法都可以实现控制参数实时在线智能整定和优化的设想;2)从可靠性(稳定性)角度看,RBFNN-PID方法存在不稳定的情况,在下一节将通过理论分析的方法进一步论证出保障稳定性的修正方法,而AWNN-PID则具有很好的稳定性;3)从算法动态和稳态特性方面看,AWNN-PID较之BPNN-PID具有更快的响应速度,BPNN-PID则具有最小的稳态误差。
3 AI-CC智能控制系统稳定性的理论研究本研究聚焦两类人工智能方法与经典的PID控制方法相结合构成两种AI-CC方法与系统,可以基于非常成熟的PID理论体系[20]进行研究,避免了非线性控制在理论分析方面遇到的难题。
本研究给出了对于高阶系统和带有延时环节的系统的稳定性分析方法,并以二阶延迟系统为例给出了理论分析和推导案例。该理论分析方法对于更加普遍的多阶系统与延时系统同样适用。
3.1 稳定性与稳定条件的理论研究AI-CC系统的开环传递函数如果描述为
| $D = {T_1}{T_2}{s^3} + ({T_1} + {T_2} + K{k_d}){s^2} + (1 + {k_p})s + K{k_i}$ | (26) |
根据式(26)和劳斯判据(Routh Criterion)方法,可以得到劳斯表为
| $\begin{array}{*{20}{c}}{{s^3}} & {{T_1} \cdot {T_2}} & {1 + {K_p}}\\{{s^2}} & {{T_1} + {T_2} + K \cdot {K_d}} & {K \cdot {K_i}}\\{{s^1}} & { - \displaystyle\frac{{\left| {\left. {\begin{array}{*{20}{c}}{{T_1} \cdot {T_2}} & {1 + {K_p}}\\{{T_1} + {T_2} + K \cdot {K_d}} & {K \cdot {K_i}}\end{array}} \right|} \right.}}{{{T_1} + {T_2} + K \cdot {K_d}}}} & {}\\{{s^0}} & {K \cdot {K_i}} & {}\end{array}$ |
当劳斯表第一列系数均为正数,系统稳定,即可以推导出系统稳定条件如式(27):
| $\left\{ \begin{array}{l}{T_1} \cdot {T_2} > 0\\{k_d} > - ({T_1} + {T_2})\\{k_p} > - 1\\{k_i} > 0\\({T_1} + {T_2} + K{k_d})(1 + {k_p}) - {T_1}{T_2}K{k_i} > 0\end{array} \right.$ | (27) |
本研究的重点是对F-PID、FA-PID、E-PID、EA- PID、BPNN-PID、RBFNN-PID、AWNN-PID智能控制方法及系统的稳定性在理论上得出保证算法。特别是将上述算法中最不稳定的RBFNN-PID算法作为重点研究案例,给出系统稳定性保障机制,对于加入稳定性保证机制的RBFNN-PID算法记作RBFNN-S-PID。
针对生产实践中最常见的具有延时环节的多阶被控对象进行理论推导,令系统中关键环节的传递函数为
已知奈奎斯特稳定性判据的等价判据:1)当
例如:被控对象模型为
|
图 7 每算法各10次计算机仿真结果 Fig.7 10 simulations of each method |
未采用稳定性保证算法的RBFNN-PID控制系统的计算机仿真结果如图9(a)所示;采用了上述稳定性保证算法的RBFNN-S-PID控制系统的计算机仿真结果如图9(b)所示。
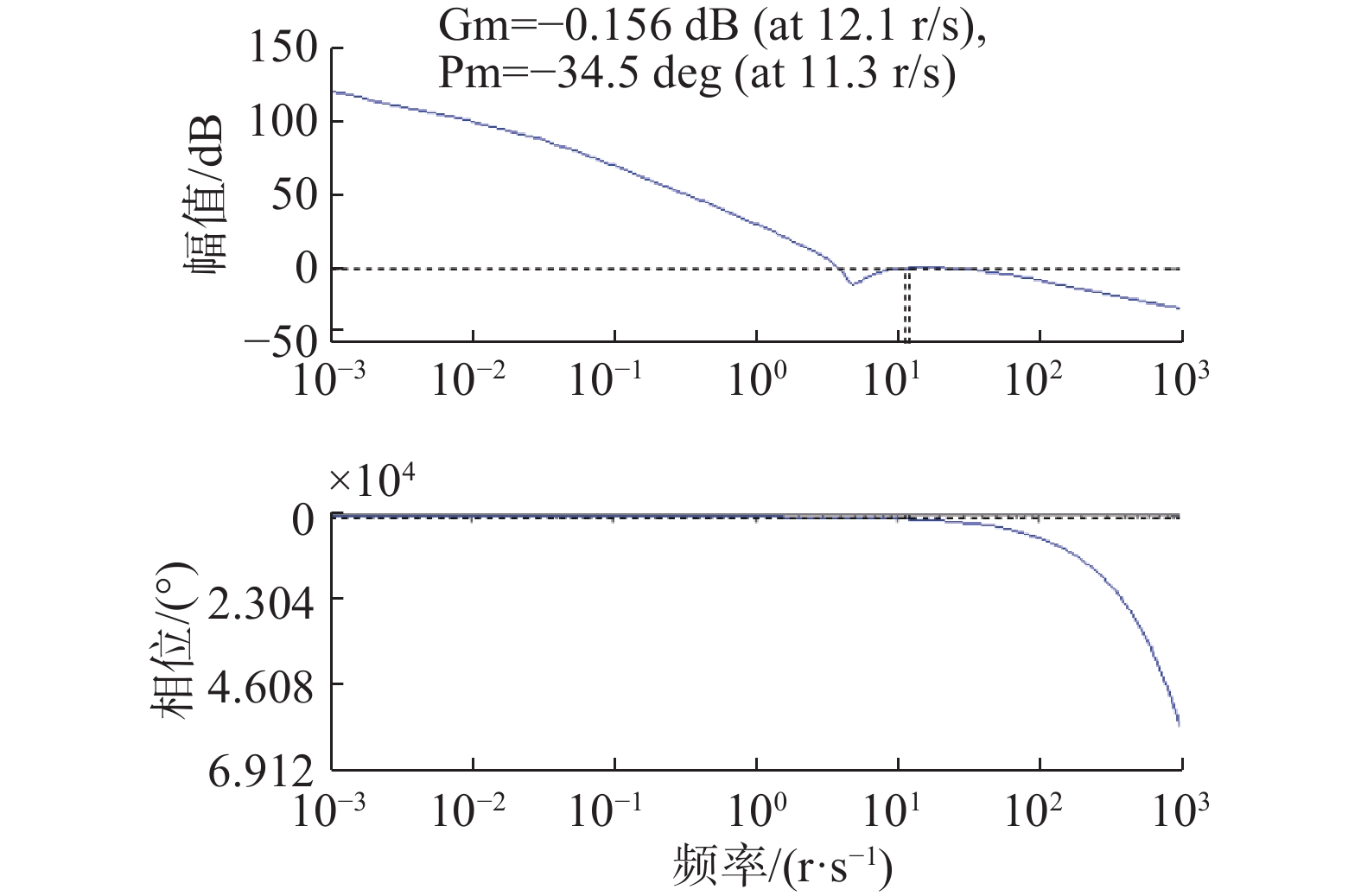
|
图 8 控制参数在线整定系统伯德图 Fig.8 Bode diagram of AI-CC |
从图9可以看出,RBFNN-S-PID系统克服了RBFNN-PID系统输出的普遍震荡、大量超调、发散不稳定的情况,输出更加平稳和稳定。验证了理论推导出的稳定性保障方法可行。
4 AI-CC智能控制系统的对比研究从实验结果的角度看:将F-PID、FA-PID、E-PID、EA-PID、BPNN-PID、RBFNN-PID、AWNN-PID各方法的性能指标进行汇总,从而进一步对各智能控制系统的智能化程度、快速性、稳态误差、抗干扰、稳定性进行对比分析,为该领域的研究者提供参考,如表6所示。
表6中的对比结果显示:1)基于规则推理的智能控制方法E-PID与EA-PID具有最好的动态性能和稳态性能,即响应速度快、稳态误差小;2)基于模糊推理的智能控制方法F-PID与FA-PID动态和稳态性能略差于前者;3)基于神经网络的智能控制方法BPNN-PID、RBFNN-PID与AWNN-PID动态和稳态性能相对最差。
从实际应用便利性和算法智能程度的角度看:1)基于神经网络优化的智能控制方法,对工程师的要求最低,即在系统运行前只需要凭经验设置一个初始参数,或者使用默认初始参数,系统在运行过程中会实时整定优化,得到最佳的控制参数;2)基于规则推理的智能控制方法的配置过程则需要工程师对规则表进行精确的配置,这个过程需要经过多次系统运行调试验证;3)基于模糊推理的智能控制方法需要配置隶属度函数的多个配置项,还需要多次系统运行调试验证,生产实践中需要对工程师进行培训才可以实施。综上所述,智能系统的智能程度和性能特征之间存在着此消彼长的辩证关系,即系统的智能程度提高,往往伴随着性能的降低,因此智能与性能之间如何取舍是需要进一步研究的重点。
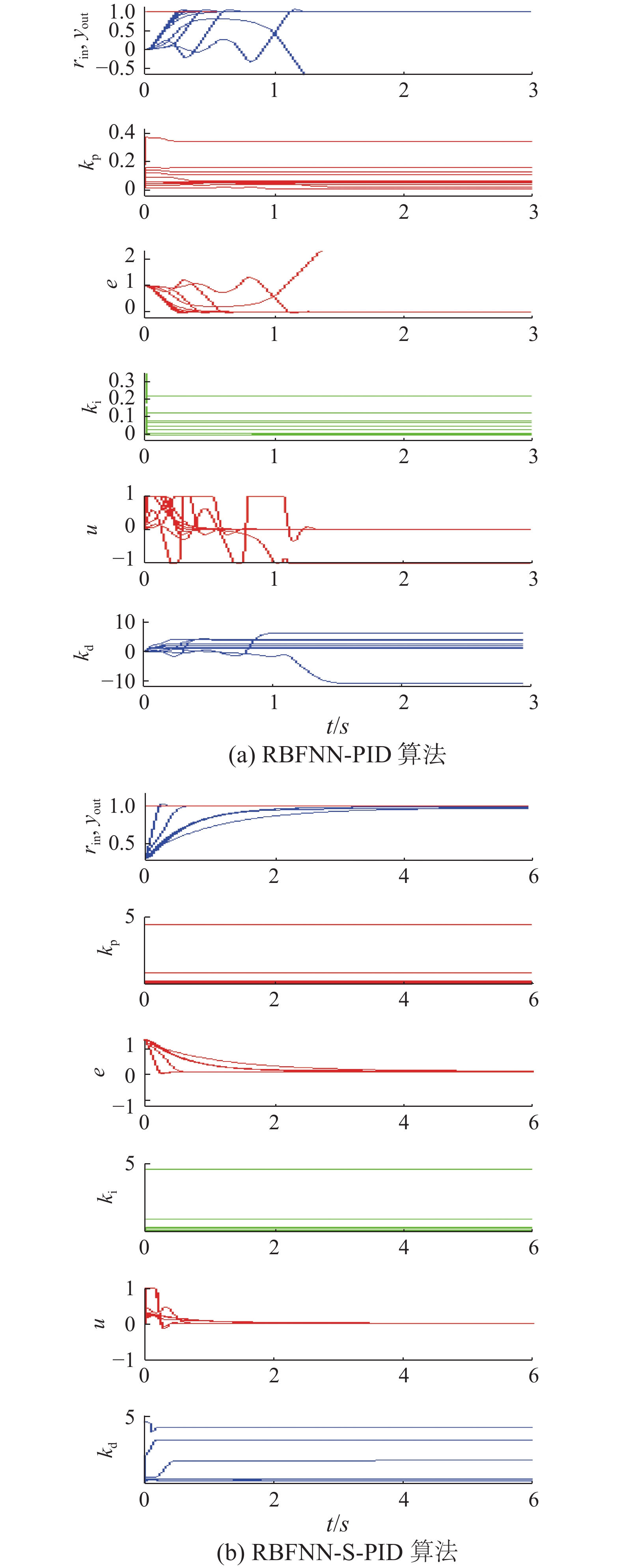
|
图 9 RBFNN-PID和RBFNN-S-PID系统仿真结果对比 Fig.9 Simulation result of RBFNN-PID and RBFNN-S-PID |
对两类多种AI-CC智能控制方法及系统的性能与实用性进行总结,如表7所示。实验结果表明:AI-CC智能控制方法随着人工智能程度的提升,在控制参数的智能能力方面具有一些优势,但是在性能方面会有所损失,与不具备智能功能的经典控制相比,个别性能会略有下降。
研究表明:控制系统的智能化程度的提升会牺牲系统所能达到的最高性能指标;系统通过精确设置,使得某项控制指标达到了极高,同时会使得系统丧失自适应能力与智能能力。
| 表 6 多种AI-CC智能控制系统仿真结果对比 Tab.6 Comparison of different intelligent control systems |
| 表 7 多种AI-CC智能控制系统的对比结果综合 Tab.7 Comparison results between different intelligent control systems |
从智能控制系统的可行性角度看,基于推理规则与神经计算的人工智能方法及经典控制系统相结合构建的AI-CC智能控制系统具有可行性。此类方法基于经典控制,是对经典控制的升级改造,因此具有坚实的理论基础和广泛的实际应用空间。
从提出的算法改进的效果看,本研究提出的EA-PID、FA-PID、AWNN-PID三项改进分别在系统的动态性能和稳态性能方面较之已有的方法有所提升。
从提出的算法稳定性和工程应用可靠性理论分析的角度看,本研究从理论上分析了上述系统的稳定性,给出了对E-PID、EA-PID、F-PID、FA-PID、BPNN-PID、RBFNN-PID、AWNN-PID多种方法保证稳定性的保证算法,使得各算法具有工程应用的可靠性保障。
本研究通过对比研究的方法,将多种AI-CC人工智能方法构建的智能控制系统进行全面对比研究,发现了智能系统的智能化程度与性能之间此消彼长的辩证统一关系。为该领域的学术研究者提供了理论推导、分析方法和仿真对比实例,为工程应用领域提供了可以基于经典系统升级改造的、可靠的智能控制系统解决方案。
| [1] |
VOLODYMYR M, KORAY K, DAVID S. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518: 529-533. ( 0) 0)
|
| [2] |
RIEDMILLER M, GABEL T, HAFNER R, LANGE S. Reinforcement learning for robot soccer[J]. Robots, 2009, 27: 55-73. ( 0) 0)
|
| [3] |
DIUK C, COHENA L. An object-oriented representation for efficient reinforcement learning[J]. Mach learn, 2008(1): 240-247. ( 0) 0)
|
| [4] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2016, 12(21): 436-444. ( 0) 0)
|
| [5] |
HINTON G. Learning multiple layers of representation[J]. Trends in cognitive sciences, 2007, 11(5): 428-434. ( 0) 0)
|
| [6] |
KRIZHEVSKY A, SUTSKEVER I, HINTON GE. Imagenet classification with deep convolutional neural networks[J]. Neural information processing systems foundation, 2012, 47: 777-780. ( 0) 0)
|
| [7] |
FARABET C, COUPRIE C, NAJMAN L, LECUN Y. Learning hierarchical features for scene labeling[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(8): 1915-1929. ( 0) 0)
|
| [8] |
SUSANTO-LEE R, FERNANDO T, SREERAM V. Simulation of fuzzy-modified expert PID algorithms for blood glucose control[C]//10th International Conference on Control, Automation, Robotics and Vision. Hanoi, Vietnam, 2008: 1583–1589.
( 0) 0)
|
| [9] |
XUE Ping, WANG Haichao, HOU Juanjuan. Based on the fuzzy PID brushless DC motor control system design[C]//International Conference on Measurement, Information and Control. Harbin, China, 2012: 703–706.
( 0) 0)
|
| [10] |
OU Kai, WANG Yaxiong, LI Zhenzhe. Feedforward fuzzy-PID control for air flow regulation of PEM fuel cell system[J]. International journal of hydrogen energy, 2015, 40(35): 11686-11695. ( 0) 0)
|
| [11] |
SHI Hongbo, HUANG Chuang. A BP wavelet neural network structure for process monitoring and fault detection [C]//The Sixth World Congress on Intelligent Control and Automation. Dalian, China, 2006(2): 5675–5681.
( 0) 0)
|
| [12] |
SHARIFIAN M B B; MIRLO A, TAVOOSI J, SABAHI M. Self-adaptive RBF neural network PID controller in linear elevator[C]//International Conference on Electrical Machines and Systems. Beijing, China, 2011: 1–4.
( 0) 0)
|
| [13] |
赵新华, 王璞, 陈晓红. 智能投球机器人模糊PID控制[J]. 智能系统学报, 2015, 10(3): 399-406. ZHAO Xinhua, WANG Pu, CHEN Xiaohong. Intelligent pitching robot based on fuzzy PID control[J]. CAAI transactions on intelligent systems, 2015, 10(3): 399-406. (  0) 0)
|
| [14] |
刘经纬, 王普, 等. 专家模糊增量式自适应的参数在线整定优化系统及方法[P]. 201110023946.6, 2012-11-07.
( 0) 0)
|
| [15] |
王普, 刘经纬, 等. 自适应小波神经网络异常检测故障诊断分类系统及方法[P]. 201110023943.2, 2012-08-30.
( 0) 0)
|
| [16] |
SHARIFIAN M B B, MIRLO A, TAVOOSI J, SABAHI M. Self-adaptive RBF neural network PID controller in linear elevator[C]//International Conference on Electrical Machines and Systems. Beijing, China, 2011: 1–4.
( 0) 0)
|
| [17] |
NIE Yanmin, HE Zhiqiang. Optimization of the main steam temperature PID parameters based on improve BP neural network[C]//International Conference on Simulation and Modeling Methodologies, Technologies and Applications. Rome, Italy, 2015: 113–116.
( 0) 0)
|
| [18] |
CHEN Zhe, FENG Tianjin, et al. The application of wavelet neural network for time series predictionand system modeling based on multiresolution learning[C]//International Conference on System, Man and Cybernetics. Tokyo, Japan, 1999(1): 425–430.
( 0) 0)
|
| [19] |
LOUSSIFI H, NOURI K, BRAIEK N B. A new efficient hybrid intelligent method for nonlinear dynamical systems identification: the wavelet kernel fuzzy neural network[J]. Communications in nonlinear science and numerical simulation, 2016, 32: 10-30. ( 0) 0)
|
| [20] |
SILVA G J, DATTA A, BHATTACHARYYA S P. New results on the synthesis of PID controllers[J]. IEEE trans on automatic sontrol, 2002, 47(2): 241-252. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


