2. Department of Nat-ural Science and Mathematics, West Liberty University, West Virginia, United States 26074
Recently,visual target tracking was widely used in security surveillance,navigation,human-computer interaction,and other applications[1, 2]. In a video sequence,targets for tracking often change dynamically and uncertainly because of disturbance phenomena such as occlusion,noisy and varying illumination,and object appearance. Many tracking algorithms were proposed in the last twenty years that can be divided into two categories: generative tracking and discriminant tracking algorithms[1, 2]. Generative algorithms (e.g.,eigen tracker,mean-shift tracker,incremental tracker,covariance tracker[2]) adopt appearance models to express the target observations,whereas discriminant algorithms (e.g.,TLD[3],ensemble tracking [4],and MILTrack[5]) view tracking as a classification problem,thus attempting to distinguish the target from the backgrounds. Here,we present a new generative algorithm.
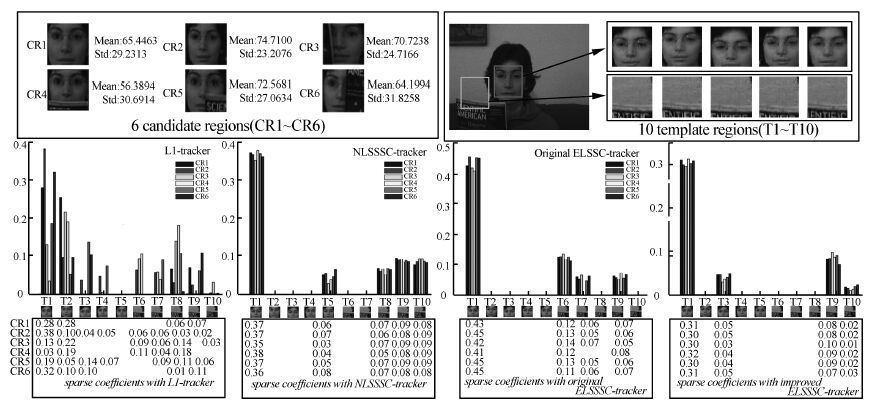
Based on sparse coding (SC; also referred to as sparse sensing or compressive sensing)[6, 7],Mei proposed an l1-tracker for generative tracking [8, 9],addressing occlusion,corruption,and some other challenging issues. However,this tracker incurs a very high computational cost to achieve efficient tracking (see section 2.1 and Fig. 1 for details),and the local structures of similar regions are ignored,which may cause the instability and even failure of the l1 -tracker. Indeed,the sparse coefficients,for representing six similar regions (CR1-CR6) under ten template regions (T1-T10) with original l1-tracker,are diversified (Fig. 3). Considering CR1 and CR4,for example,we can see that although the latter is almost the partial occlusion version of the former,their sparse representations are very different. Tracking CR4 (the woman's face) may fail,because the tracker is likely to incorrectly consider the region T8 (the book) as its target.

|
| Fig. 1 Original l1-tracker algorithm |
|
| Fig. 3 Comparisions of sparsity and stability with the original l1-,NLSSSC-,and our ELSSC-optimization. The sparse coefficients only are accurated to the second decimal place. |
Contrary to expectations,Xu proved that a sparse algorithm cannot be stable and that similar signals may not exhibit similar sparse coefficients[10]. Thus,a trade-off occurs between sparsity and stability when designing a learning algorithm. In addition,instability in the l1-optimization problem affects the performance of the l1-tracker.
Lu developed a NLSSS-tracker (NLSSST) based on SC applying a non-local self-similarity constraint by introducing the geometrical information of the set of candidates as a smoothing term to alleviate the instability of the l1-tracker[11]. However,its low efficiency (even slower than the original l1-tracker,Table 4) restricts its applicability in real-time tracking. In this study,motivated by the robustness of the l1-tracker and stability of NLSSST,we propose a novel tracker,called ELSS-tracker (ELSST),that is both robust and efficient. The main contributions of this study are as follows:
1)An efficient tracker,i.e.,ELSST,is developed by considering the local structure of the set of target candidates. In contrast to the Lu5s[11] and Mei5s-tracker[8, 9],our tracker is more stable and sparse.
2)The proposed tracker shows excellent performance in tracking different video sequences with regard to scale,occlusion,pose variations,background clutter,and illumination changes.
The rest of this study is organized as follows: l1- and NLSSS-tracker are introduced in section 2; in section 3,we analyze the disadvantages of these two trackers and propose our tracker; experimental results with our tracker and four comparison algorithms are reported in section 4; the conclusion and future work are summarized in section 5.
1 Related works 1.1 Sparse coding and the l1-trackerSparse coding is an attractive signal reconstruction method proposed by Candes[6, 7] that reconstructs a signal y∈Rm×1 with an over-complete dictionary D∈Rm×(n+2m) with a sparse coefficient vectorc∈Rn×1. The SC formulation can be written as the l0-norm-constrained optimization problem as follows:

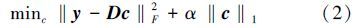
Based on SC,Mei presented a nice l1-tracker for robust tracking[8, 9] (Fig. 1). Considering that the target is located in the latest frame,the l1-tracker is initialized in the new arrival frame and N candidate regions are generated with Bayesian inference (Fig. 1a,b). With n templates learned from previous tracking and 2m trivial templates (m positive ones and m negative ones,where m is the dimension of 1D stretched image,Fig. 1c),Eq.(2) can be solved (Fig. 1d,e,f). With positive and negative trivial templates,Mei added a non-negative constraint c≥0 in Eq.(2),with which the reconstruction errors of all candidate regions with SC coefficients can be used to determine the weights for each candidate,and the object in the new arrival frame can be located with the sum of the weighted candidates. The dictionaries updating strategies can be seen in[8, 9].
1.2 Non-local self-similarity based sparse coding for tracking (NLSSST)Recently,Xu indicated the trade-off between sparsity and stability in sparse regularized algorithms[10]. Moreover,Yang pointed out the same A-optimization issue in pattern classification[12]. Based on the fact that lots of similar regions exist in all N candidates generated by Bayesian inference,Lu proposed his tracker with the non-local self-similarity constraint as

 ,where h is a parameter enforcing similarity,and sj is the normalization factor. The weight wji measures the similarity between the K-neighborhood of yj and yi. Lu’s algorithm actually attempts to solve the following:
,where h is a parameter enforcing similarity,and sj is the normalization factor. The weight wji measures the similarity between the K-neighborhood of yj and yi. Lu’s algorithm actually attempts to solve the following:

Taking the solution of the l1-tracker from Eq.(2) as the initial coefficients c0,Eq.(4) can be solved through iterative computations[11]. However,the high computational cost of the original l1-tracker and iterative procedure for maintaining the neighborhood constraints of sparse coefficients make NLSSST inefficient in achieving real-timing tracking. In contrast to Fig. 1,the schematic diagram of NLSSST presented in Fig. 2,includes an additional neighborhood constraint between yi and NK (yi).
|
| Fig. 2 Lu's NLSSST Algorithm |
To circumvent the heavy computation burden of the l1-tracker and NLSSST (Table 4),we propose an efficient tracker,called ELSST,that considers the local Euclidean structures of the candidates.
2.1 Original euclidean local structure constraint sparse coding (Original ELSSC)It is evident from Eq. (4) that NLSSST attempts to solve a double l1-norm problem. However,it is well known that the l2-norm is much more commonly used for measuring the distance between two vectors and is much easier to optimize than the l1-norm. Thus,we take the former to measure the relationships between the sparse coefficient vectors,which are close to each other,i.e.,the Euclidean local-structure constraint,and the latter l1-norm of C to maintain the sparsity of the optimization as follows:
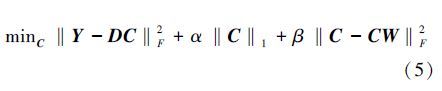
Equation (5) is the objective function of our Euclidean local structure constraint-based SC and can be solved through iterative computation. In particular,at the t-th iteration,for a single candidate yi in Y,Eq. (5) can be written as follows:
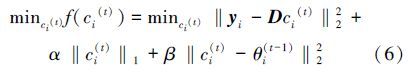
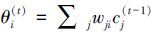 . At the t-th iteration for the optimization of ci,cj,i≠j is fixed. Therefore,we can regard θi(t-1) as a constant. To solve Eq. (6),we introduce the following surrogate function as presented in [11]:
. At the t-th iteration for the optimization of ci,cj,i≠j is fixed. Therefore,we can regard θi(t-1) as a constant. To solve Eq. (6),we introduce the following surrogate function as presented in [11]:
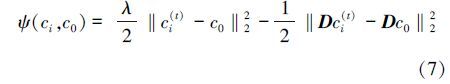
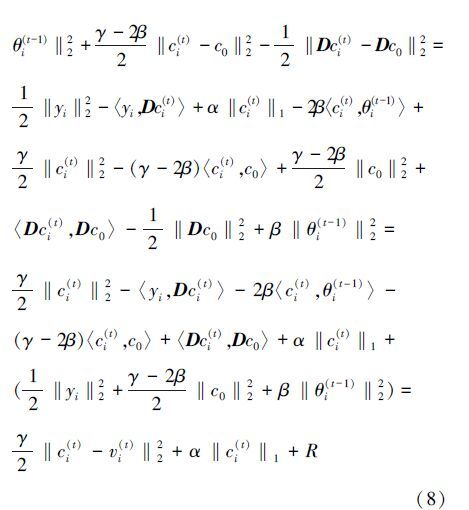

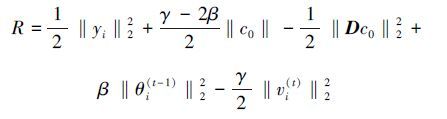


| Input:Given N data points Y=[y1 … yN]∈R m×N,over-complete dictionary D∈Rm×(n+2m) |
| Output:Sparse matrix C=[c1 … cN] ∈R(n+2m)×N |
| Parameters: Maxiumn iteration number J=10,neighborhood size K=5,all-zero vector c0 , α=0.01,β=0.5,γ=0.001 |
| 1:For each point yi,compute the nearest K neighborhoods NK(yi) and weights wji |
| 2:Compute the SVD-decomposition of D=UΣVT,where V∈R(n+2m)×(n+2m) |
| 3:compute ‖DT D‖,and set ‖DTD ‖+2β randomly |
| 4:For i=1:N |
| 5: For t=1:J |
| 6: If ‖ci(t)-c i(t-1)‖2<τ,break inner iteration |
7:Compute 
|
| 8: Represent xi(t) with sparse coefficient vector ci(t),i.e.,optimize γ/2‖xi(t)-Vci(t)‖ 22+α‖ci(t)‖1 |
| 9: End |
| 10:End |
If m in Eq. (10) is large,it is time-consuming to obtain the optimization result ci, as that in l1-optimization and NLSSSC. Fortunately,in terms of SVD and the structure of D (Figs. 1 and 2),we have

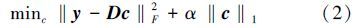
Based on the above algorithm,our tracker can be obtained with the framework of the original l1-tracker[8, 9] (Table 2). We need to iteratively solve the large-scale l1-optimization problem in Eq. (10) twice,up to three times for each candidate in the algorithm,and more than five times in NLSSST. The initial sparse coefficients c0 are considered as all-zero vectors and iteratively solve the problem without any l1-optimization issues,as in Table 1 in [11]. Nevertheless,we find that,in NLSSST,it is more effective and accurate to initialize c0 as the solution of the l1-optimization problem. Therefore,the computation complexity of our tracker is of the same order of magnitude as that of the l1-tracker and NLSSST. When we resize all n= 10 targets and n = 200 candidate regions to 40 × 40,i.e.,m= 1 600 (Figs. 1 and 2),then the over-complete dictionary D is 1 600 × 3 210 and the orthogonal matrix V is 3 210 × 3 210 in Eq. (10). It is very difficult to solve the corresponding l1-optimization problem with such a D (in l1-tracker and NLSSST) or V (in our ELSST).
With the improved ELSSC,Σ′ is the first ten rows of Σ ,and V′ consists of the first ten rows and first ten columns of V. Thus,each iteration of each candidate region in ELSST can be reduced from the large-scale l1-optimization problem to a much smaller one because of the much smaller scale V′∈R10×10. To overcome the problem of occlusions in tracking,the analogous trivial templates are used to construct the new dictionaryV″∈ R10×30,i.e.,a ten-ordered identity matrix and ten-ordered negative identity matrix.
| Input:Given a video stream for tracking,location of the target l1 in frame #1 |
| Output:Tracking results of each frame |
| 1:Set s=1,select 10 template regions extremely near the target in #1,then resize and stretch them to be T∈R1 600×10 |
| 2:While not reach the end of the video sequence,s←s+1 |
| 3:Pick N=200 candidate regions around the latest target location ls-1 in frame #s,and stretch to be Y∈R1 600×200 |
| 4:Construct D with T,positive and negative identity matries,likewise in Fig. 1 and Fig 2 |
| 5:Solve ELSSC-optimization with Y and D in Table 1,and denote the optimization result as ci(s) |
6:Compute the reconstruct errors ei(s)=‖xi(s)-Vci(s)‖22 and the normalized weight 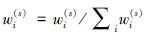 ,where
wi(s)=exp(-ei(s)/α) ,where
wi(s)=exp(-ei(s)/α)
|
| 7:Locate the object for tracking with the weighted sum of all 200 candidate regions and wi(s) in frame #s |
| 8:Select 10 regions that extremely nearby the object as the new target templates T |
| 9:End |
In order to evaluate the proposed tracker,experiments on 12 video sequences were conducted,including Surfer,Dudek,Faceocc2,Animal,Girl,Stone,Car,Cup,Face,Juice,Singer,Sunshade,Bike,Car Dark,and Jumping[17, 18, 19]. These sequences covered almost all challenges in tracking,including occlusion (even heavy occlusion),motion blur,rotation,scale variation,illumination variation,and complex background. For comparison,we used four state-of-the-art algorithms with the same initial positions and the same representations of the targets. They were the incremental learning-based tracker (IVT,a common discriminant tracker) [14],the covariance-based tracker (CovTrack,a generative tracker on Lie-group)[15],the l1-tracker (a generative tracking method)[8, 9],and the NLSSST[11].All the experiments were run on a computer with a 2.67 GHz CPU and a 2 GB memory.
The main parameters used in our experiments are set as follows: the number of candidate regions n=200,the number of template regions is n= 10,and the candidates and targets are resized to 40×40.
3.2 Experimental results for sparsity and stabilityThe stability and sparsity of the original sparse coding,the NLSSSC,and the original and improved ELSSC were verified. The experiments were designed with the Face sequence in the VOT 2013 benchmark dataset[18] as follows: six similar regions were represented (CR1,…,CR6,their means and standard derivations illustrate the similarity) sparsely with template T=[T1,…,T10]∈R1 600×10 from two regions apart from each other (the red region and the green one). Evidently,T is over-completed,and the entire dictionary D∈R1 600×3 210is constructed likewise in Figs. 1 and 2.
The sparse coefficients of CR1,…,CR6 generated with the l1-,the NLSSSC-,the original ELSSC-,and the improved ELSSC-optimization are plotted in Fig. 3. In particular,six similar regions have very different representation coefficients,when using the original l1-optimization problem,which ignores the structure information between regions. The results of the other three algorithms are much more stable,because of preservation of the structural information. If two regions are similar to each other,they also have similar sparse coefficients. This improves the robustness of tracking; otherwise,the tracker may degenerate or even fail to track. CR4 for example,with l1-optimization,can be represented by T2, T8, T6, T7,and T1,and the tracker may fail to track the top of the book. Meanwhile,experimental results show that,NLSSSC and our two ELSSC are sparser than the original l1-optimization problem.
3.3 Experimental results for visual target trackingWe evaluate the investigated algorithms comparatively,using the center location errors,the average success rates,and the average frames per second. The results are shown in Figs. 4&5 and in Tables 3&4. The templates of NLSSST,the original ELSST,and the improved ELSST are shown in Fig. 4(g-o). Overall,our original and improved trackers outperform the other state-of-the-art algorithms.
For occlusion,five algorithms,except IVT,function satisfactorily,especially at #206,#366 of the Dudek sequence in Fig. 4(b) (the head in tracking is covered by the hand and glasses),#143,#265,#496 of the Faceocc2 sequence in Fig. 4(c) (the head in tracking is covered by the book),#85,#108,#433 of the Girl sequence in Fig .4 (e) (the head in tracking turns right,turns back,and blocks someone else),and #56,#104,#301 of the Face sequence in Fig. 4(i) (the head in tracking is also covered by the book). After the target recovers from occlusion,these five trackers can seek it quickly. IVT works poorly,even loses the target in #10 of the Girl sequence (Fig. 5(e)),because the number of positive and negative samples is limited (considering the learning efficiency),and the incremental updating of the classifier in IVT is less effective. CovTracking has a large size of candidates (based on the definition of integral image,the feature extraction of these candidates is so fast,that its cost can be ignored),which makes it robust for occlusion,scale variation,and blur. NLSSST and our original and improved trackers all work well,when the targets are occluded; our two trackers work even better.
For motion blur,our two trackers work better than IVT and the original l1-tracker. Moreover,CovTracking also reveals its ability to handle blur (e.g.,#4,#9,and #38 in Fig. 4(d,o). In the former sequence,the animal runs and jumps fast (motion blur) with a lot of water splashing (occlusion),while in the latter,the man ropes skipping and the camera cannot take the clear face of the man. IVT and l1-tracker fail both from #4 in Fig. 4(d),and never recover after that. Our original and improved ELSS lost the target in #31 and #41,then recovered in #33 and #44 (Fig. 4(d)). In #12 to #21 and #44 to #71,the improved ELSST works better than original ELSST,CovTracking,l1-tracker,and NLSSST.

|
| Fig. 4 Some tracking results |
For rotation and scale variation,our trackers also perform robustly (Figs. 4(a,c,e,g,j) and 5(a,c,e,g,j). When the surfer falls forward and backward,the girl turns left and right,moves towards and away from the camera,the man turns left and right,the car turns over,and the juice bottle becomes bigger and smaller in Surfer,Girl,Faceocc2,Car,and Juice sequence,respectively,five trackers except IVT perform well,especially the NLSSS-tracker and our two ELSSC-trackers.
In a complex background and with high illumination variance (Fig. 4(f)),there are many similar stones to track. The l1-tracker and our two trackers work better than other three trackers. Cov-tracker fails,because it extracts edge information of targets as one dimension of features,and in this sequences,edge of targets are ambiguous and hard to be distinct. Similar results are obtained from Fig. 4(h,l,m).
Table 3 summarizes the average success rates. Given the tracking results RT and the ground-truth RG,we use the detection criterion in the PASCAL VOC challenge[16],i.e.,
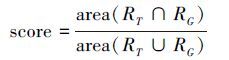
| Video | IVT | CovTrack | l1-tracker | NLSSST | ELSST1 | ELSST2 |
| Sufer | 0.051 5 | 0.477 0 | 0.038 8 | 0.464 6 | 0.466 7 | 0.405 2 |
| Dudek | 0.201 1 | 0.421 6 | 0.621 5 | 0.652 8 | 0.672 6 | 0.660 4 |
| Faceocc2 | 0.455 3 | 0.391 8 | 0.608 4 | 0.457 9 | 0.574 7 | 0.464 1 |
| Animal | 0.021 8 | 0.270 1 | 0.033 6 | 0.369 2 | 0.407 8 | 0.411 7 |
| Girl | 0.022 8 | 0.217 1 | 0.486 9 | 0.485 3 | 0.400 6 | 0.469 3 |
| Stone | 0.097 4 | 0.111 4 | 0.583 4 | 0.410 9 | 0.661 1 | 0.657 2 |
| Car | 0.060 7 | 0.185 8 | 0.095 6 | 0.341 8 | 0.327 8 | 0.382 5 |
| Cup | 0.630 0 | 0.376 9 | 0.559 8 | 0.573 8 | 0.523 8 | 0.563 7 |
| Face | 0.334 1 | 0.280 6 | 0.047 9 | 0.524 8 | 0.549 6 | 0.582 7 |
| Juice | 0.074 3 | 0.421 8 | 0.511 1 | 0.529 9 | 0.518 6 | 0.583 5 |
| Singer | 0.332 6 | 0.136 1 | 0.118 4 | 0.579 0 | 0.478 1 | 0.565 1 |
| Sunshade | 0.048 1 | 0.180 3 | 0.525 7 | 0.534 8 | 0.474 3 | 0.494 8 |
| Bike | 0.057 6 | 0.372 1 | 0.045 1 | 0.443 8 | 0.360 8 | 0.391 7 |
| CarDark | 0.083 1 | 0.308 7 | 0.079 0 | 0.011 0 | 0.420 8 | 0.373 7 |
| Jumping | 0.057 7 | 0.275 5 | 0.071 1 | 0.084 7 | 0.453 0 | 0.450 5 |
| The best two results are shown in bold. Our original and improved algorithms are shown in the last two columns,respectively. | ||||||
to evaluate the success rate. In general,from the above analysis,we find that our original and improved ELSSC-trackers perform almost the same,and the former is slightly better,especially in the Dudek,Faceocc2,Surfer,Stone,CarDark,and Jumping sequences (Fig. 5(a,b,c,f,n,o). However,we also find from Table 4,which summarizes the average frames per second,that the improved ELSST works much faster than the original ELSST and almost all the other trackers; IVT is faster than the improved ELSST when dealing with Surfer and Dudek sequences,but its success rate is much worse than that of the improved ELSST. It is sensitive under the phenomena of occlusion,rotation,and target motion blur. The original l1-tracker performs well in most frames,but it is also time-consuming and fails to track sometimes; Cov-Tracking is suitable for occlusion and rotation,but fails when facing a complex background.

|
| Fig. 5 Quantitative evaluation in terms of center location error (in pixel) |
| Video | IVT | CovTrack | l1-tracker | NLSSST | ELSST1 | ELSST2 |
| Sufer | 2.864 9 | 1.570 7 | 0.035 8 | 0.014 1 | 0.015 6 | 2.346 9 |
| Dudek | 3.321 1 | 1.245 4 | 0.038 8 | 0.017 1 | 0.017 9 | 3.245 4 |
| Faceocc2 | 2.788 6 | 1.127 8 | 0.018 0 | 0.010 7 | 0.014 2 | 3.127 8 |
| Animal | 1.897 9 | 1.253 4 | 0.031 2 | 0.015 0 | 0.007 1 | 3.253 4 |
| Girl | 1.654 8 | 1.220 9 | 0.037 6 | 0.016 7 | 0.009 8 | 3.220 9 |
| Stone | 1.290 3 | 1.889 0 | 0.027 1 | 0.014 4 | 0.014 6 | 4.113 8 |
| Car | 3.684 1 | 2.850 2 | 0.062 1 | 0.052 5 | 0.036 5 | 6.225 3 |
| Cup | 7.817 5 | 3.547 9 | 0.079 8 | 0.067 7 | 0.053 8 | 6.394 9 |
| Face | 6.742 2 | 2.896 1 | 0.054 3 | 0.041 7 | 0.054 6 | 6.168 1 |
| Juice | 7.048 9 | 3.929 7 | 0.063 5 | 0.066 5 | 0.058 6 | 5.473 8 |
| Singer | 6.095 9 | 2.802 6 | 0.019 5 | 0.068 3 | 0.048 1 | 6.189 1 |
| Sunshade | 7.302 7 | 2.790 5 | 0.071 3 | 0.058 7 | 0.078 1 | 6.060 1 |
| Bike | 6.974 7 | 2.719 2 | 0.016 3 | 0.032 0 | 0.021 0 | 5.840 0 |
| CarDark | 3.704 1 | 1.395 1 | 0.022 6 | 0.055 2 | 0.029 5 | 2.422 1 |
| Jumping | 7.329 6 | 2.608 0 | 0.052 0 | 0.047 6 | 0.057 9 | 3.551 9 |
| The best two results are shown in bold. Our original and improved algorithms are shown in the last two columns,respectively . | ||||||
In this study,to deal with sparsity and instability in the l1-optimization problem[10, 11, 12] and the high time complexity of the NLSSSC-tracker [11],we propose a novel efficient tracker,i.e.,the Euclidean local-structure constraint based sparse coding (ELSSC). Our new algorithm is a l1-tracker with a reconstructed over-complete dictionary,which is different from that in the original l1-tracker and NLSSSC-tracker. Moreover,we simplify the large-scale l1-optimization problem in our tracker to a much smaller one in our improved ELSSC-tracker.
Compared with the original l1-tracker,our ELSSC-tracker introduces the structure information among the candidate regions generated by the Bayesian inference to the l1-tracker,similar to that in the NLSSSC-tracker. With our derivation,the optimization procedure of our tracker (Eq.(10)) can be solved as that in the l1-optimization but very differently from that in the NLSSSC. Furthermore,our improved tracker is much more efficient than the l1-tracker and NLSSSC-tracker. Our experiments demonstrate the sparsity,stability,and efficiency of our tracker.
| [1] | ZHANG Shengping, YAO Hongxun, SUN Xin, et al. Sparse coding based visual tracking:review and experimental com-parison[J]. Pattern recognition, 2013, 46(7):1772-1788. |
| [2] | YILMAZ A, JAVED O, SHAH M. Object tracking:a sur-vey[J]. ACM computing surveys (CSUR), 2006, 38(4):1-45. |
| [3] | KALAL Z, MIKOLAJCZYK K, MATAS J. Tracking-learn-ing-detection[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(7):1409-1422. |
| [4] | AVIDAN S. Ensemble tracking[J]. IEEE transactions on pattern analysis and machine intelligence, 2007, 29(2):261-271. |
| [5] | BABENKO B, YANG M H, BELONGIE S. Visual tracking with online multiple instance learning[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recogni-tion (CVPR). Miami, USA, 2009:983-990. |
| [6] | CANDÈS E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE, signal processing magazine, 2008, 25(2):21-30. |
| [7] | CANDÈS E J, ROMBERG J, TAO J. Robust uncertainty principles:exact signal reconstruction from highly incom-plete frequency information[J]. IEEE transactions on infor-mation theory, 2006, 52(2):489-509. |
| [8] | MEI Xue, LING Haibin, WU Yi, et al. Minimum error bounded efficient l1 tracker with occlusion detection[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Colorado, USA, 2011:1257-1264. |
| [9] | MEI Xue, LING Haibin. Robust visual tracking and vehicle classification via sparse representation[J]. IEEE transac-tions on pattern analysis and machine intelligence, 2011, 33(11):2259-2272. |
| [10] | XU Huan, CARAMANIS C, MANNOR S. Sparse algo-rithms are not stable:a no-free-lunch theorem[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 34(1):187-193. |
| [11] | LU Xiaoqiang, YUAN Yuan, LU Pingkun, et al. Robust visual tracking with discriminative sparse learning[J]. Pat-tern recognition, 2013, 46(7):1762-1771. |
| [12] | YANG Jian, ZHANG Lei, XU Yong, et al. Beyond sparsi-ty:the role of L1-optimizer in pattern classification[J]. Pattern recognition, 2012, 45(3):1104-1118. |
| [13] | DAUBECHIES I, DEFRISE M, DE MOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on pure and ap-plied mathematics, 2004, 57(11):1413-1457. |
| [14] | ROSS D A, LIM J, LIN R S, et al. Incremental learning for robust visual tracking[J]. International journal of com-puter vision, 2008, 77(1-3):125-141. |
| [15] | PORIKLI F, TUZEL O, MEER P. Covariance tracking u-sing model update based on lie algebra[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York, USA, 2006:728-735. |
| [16] | EVERINGHAM M, VAN GOOL L, WILLIAMS C K I, et al. The pascal visual object classes (VOC) challenge[J]. International journal of computer vision, 2010, 88(2):303-338. |
| [17] | WU Yi, LIM J, YANG M H. Online object tracking:A benchmark[C]//Proceedings of IEEE Conference on Com-puter Vision and Pattern Recognition (CVPR). Portland, USA, 2013:2411-2418. |
| [18] | KRISTAN M, PflUGFELDER R, LEONARDIS A, et al. The visual object tracking VOT2013 challenge results[C]//Proceedings of IEEE International Conference on Computer Vision Workshops (ICCVW). Sydney, Austral-ia,2013:98-111. |
| [19] | SONG Shuran, XIAO Jianxiong. Tracking revisited using RGBD camera:unified benchmark and baselines[C]//Proceedings of IEEE International Conference on Computer Vision (ICCV). Sydney, Australia, 2013:233-240. |



