2. 广西师范大学计算机科学与信息工程学院, 广西桂林 541004
2. College of Computer Science and Information Technology, Guangxi Normal University, Guilin 541004, China
波兰的数学家Pawlak在20世纪80年代提出的粗糙集是一种新型的用来处理不完全、不精确与不相容的数学工具和理论[1, 2]。经过了30多年的研究和发展,粗糙集理论已在知识发现、数据挖掘、模式识别等领域得到了大量应用[3, 4]。属性约简作为粗糙集理论的重要研究内容,已被广大学者所研究,提出了围绕完备决策表的属性约简算法,但是现实生活中的数据往往存在误差,缺失及多源等特征。如何对不完备决策表进行直接处理,已成为粗糙集理论的一个研究热点[4]。近年来针对不完备决策表的研究也取得了显著的进步,已有学者提出很多有效的不完备决策表属性约简算法[5, 6, 7, 8, 9, 10, 11]。知识粒度[12, 13]作为粗糙集理论中度量属性约简的重要方法之一,被广泛运用于不完备属性约简算法。文献[5]以属性重要性为启发信息,设计了一个基于知识粒度的属性约简算法[5];文献[6]通过不断向核属性集中添加属性的方法,设计出一种基于相对知识粒度的不完备决策表属性约简算法[6];文献[7]定义了一个粒度差别矩阵,进而设计了基于知识粒度的不完备决策表的属性约简算法[7],其时间复杂度 为max{O(|C|2|U||Upos|),O(|K||C|U|)},其中K=max{|TC(xi)|,xi∈U},其空间复杂度为max{O(|C||U||Upos|),O(|U|)};文献[8]给出了一个计算条件属性频率的公式,设计一个基于知识粒度的属性约简算法[8];文献[9] 设计了一种基于对象矩阵的属性约简算法[9];文献[11]提出简化差别矩阵定义,设计了一种快速的属性约简算法[11];文献[12]中根据区分对象对集的思想,设计了基于正区域的属性约简算法[12];文献[13]根据粒计算的思想构建了粒矩阵,在此基础上,设计了属性约简算法。文献[14]在粒计算属性约简算法的基础上进行了改进,得到一个新的算法。上述算法大多因为要多次计算知识粒度,导致计算效率都不太理想,为此设计出基于知识粒度的高效属性约简算法具有非常重要的现实意义[5]。
差别矩阵作为粗糙集理论的重要技术之一,被广泛应用,但是求解差别矩阵费时,本文引入了基于粒度的差别矩阵,利用条件属性在区分对象时出现频率的属性约简思想,设计一个基于粒度差别矩阵计算属性频率的启发函数。
1 粗糙集基本概念
定义1[3] 五元组
S=(U,C,D,V,f)是一个不完备决策表,其中U={x1,x2,…,xn}表示对象的非空有限集合,称为论域;
C={c1,c2,…,cm}表示条件属性的非空有限集合;
D表示决策属性的非空有限集合,且
C∩D=∅;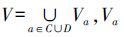 Va,Va是属性a的值域;f:U×C∪D→V是一个信息函数,它对一个对象的每一个属性赋予一个信息值,即∀a∈C∪D,x∈U,有f(x,a)∈Va。
Va,Va是属性a的值域;f:U×C∪D→V是一个信息函数,它对一个对象的每一个属性赋予一个信息值,即∀a∈C∪D,x∈U,有f(x,a)∈Va。
在五元组中,如果至少有一个属性a∈C,使得 Va包含空值(用*表示),即至少有一个属性a∈U,存在一个a∈U,使得f(x,a)=*,称之为不完备决策表。
定义2[3] 在不完备决策表 s=(U,C,D,V,f)中,令B⊆C,定义U上的容差关系 T(B)为T(B)={(x,y)∈U×U|∀b∈B},f(x,b)= f(y,b)∨f(x,b)=*∨f(y,b)=*}。用TB(x)表示在B中与x具有容差关系的全体对象集{y∈U|(x,y)∈T(B)}。
定义3[16] 在不完备决策表
S=(U,C,D,V,f)中 ,知识B⊆C的知识粒度定义为GD(B)=
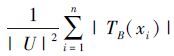 .其中U={x1,x2,…,xn},|X|表示集合X的基数. 显然有CD(∅)=0。
.其中U={x1,x2,…,xn},|X|表示集合X的基数. 显然有CD(∅)=0。
性质1[16] 设S=(U,C,D,V,f)是一个不完备信息系统,知识B⊆C的知识粒度定义为 GD(B),则1/|U|≤GD(B)≤1。
性质2[16] 设 S=(U,C,D,V,f)是一个不完备信息系统,其中P,Q⊆C,如果 ∀i∈{1,2,…,|U|}有TP(xi)⊆TQ(xi),则GD(P)≤GD(Q)。
知识粒度可以描述知识的区分能力,知识粒度越小,其区分能力越强,反之区分能力越弱[5]。
定义4[5] 在不完备决策表 S=(U,C,D,V,f)中 ,知识B(B⊆C) 是C关于D的一个知识粒度的属性约简,当且仅当B满足条件:
1)GD(B)=GD(C);
2)∀b∈B⇒GD((B-{b}))≠GD(C)。
定义5[7] 在不完备决策表
S=(U,C,D,V,f)中,∀B⊆C,U/D={D1,D2,…,DK}表示由决策属性集D对论域U的划分,称 为C关于D的正区域,设条件属性对论域的划分为U/C={[xi1]c,
[xi2]c,…,[xik]c},Upos={
xij|[xij]c⊆POSC(D)},Uneg=
U-Upos。
为C关于D的正区域,设条件属性对论域的划分为U/C={[xi1]c,
[xi2]c,…,[xik]c},Upos={
xij|[xij]c⊆POSC(D)},Uneg=
U-Upos。
定义6[11] 设在一个不完备决策表 S=(U,C,D,V,f)中,U=Upos∪Uneg,定义粒度差别矩阵M=(m(i,j)),其元素定义如下:
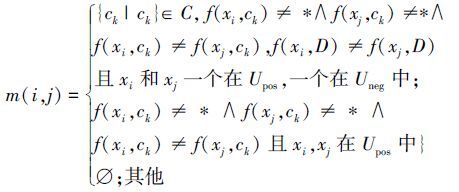
定义7[7] 设M =(m(i,j))为不完备决策表S=(U,C,D,V,f)的粒度差别矩阵,∀B⊆C,若B满足:
1)∀∅≠m(i,j)∈M,有B∩m(i,j)≠∅;
2)∀a∈B,B′=B-{a}均不满足(1)。
则称B是C关于D的一个属性约简,此约简记为基于粒度差别矩阵的属性约简。
定理1 在不完备决策表S=(U,C,D,V,f) 中,有RC=∪a∈CR{a}。
证明 由定义1知:命题显然成立。
定理2[7] 基于知识粒度的属性约简定义与基于粒度差别矩阵的属性约简定义是等价的。
定理2说明基于知识粒度的属性约简可以转化到粒度差别矩阵上进行。
针对不完备决策表,文献[7]中给出了一个基于粒度差别矩阵的属性约简算法,其时间复杂度为max{O(|C|2|U pos||U|),O(K|U||C|)}。算法对粒度差别矩阵进行遍历,若只包含一个条件属性就将其放入属性约简中,并去掉差别矩阵中任何含有该条件属性的差别元素,直至差别矩阵为空。该算法 虽然有效降低了时间复杂度,但是构造粒度差别矩阵仍然需要占用大量的空间,对于处理大型数据集仍然具有一定的难度。
经分析,算法中在粒度差别矩阵中出现的条件属性才是能区分对象的条件属性,由于构造粒度差别矩阵耗费空间,参考文献[16]的方法,设计一种计算粒度差别矩阵中含有的条件属性频率的函数,然后给出计算该函数的快速算法,无须构造粒度差别矩阵就可以将其中能有效区分对象的条件属性找出,以降低算法的时间和空间复杂度。
3 计算属性频率的启发函数
定理3 在决策表
S=(U,C,D,V,f)中,B⊆C,U/B={A1,A2,…,Al}
,Ai/{a}={Ai1,Ai2,…,Aik},
Aij=posi∪Negj,U=Upos∪Uneg,其中posi=Aij∩U
pos,Negj=Aij∩Uneg,posi/D={Di1,Di2,…,DiD},Negj/D=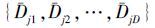 。令si=|posi/D|=
。令si=|posi/D|= |D||Dij|=|posi|,则所有集合中属于正域的集合对D划分posi/D总和为S=
|D||Dij|=|posi|,则所有集合中属于正域的集合对D划分posi/D总和为S=
 S=
S= posi|,所有集合中属于正域的所有集合对D划分
posi/D中决策值相同集合总数为
Tj=
posi|,所有集合中属于正域的所有集合对D划分
posi/D中决策值相同集合总数为
Tj= Dij。
Dij。
根据定义6,粒度差别矩阵中包含的条件属性可由两部分产生,设对象都在Upos里产生的条件属性的个数为
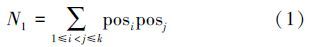
两个对象一个在Upos中,另一个在 Uneg中,产生的条件属性频率为N2,则
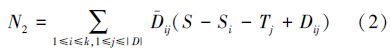
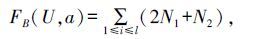
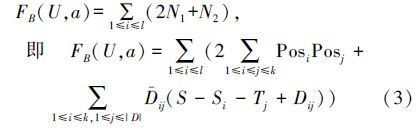
证明 由粒度差别矩阵的定义知,计算 Ai/{a}={Ai1,Ai2,…,Aik}产生的条件属性频率,可分两部分计算,一种是对象都在 Upos 中;另一种是一个在Upos中,而另一个在Uneg中的。
1)若两个对象都在Upos中,由划分的定义知,在同一个划分集合里的两个对象值相等,即只有不同划分集合里才有可能产生有效区分对象的条件属性。则只有不同划分集合的
Upos之间才能产生条件属性频率;若两个对象都在Upos中,产生的条件属性频率为N1=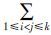 posiposj,任意两个划分集合都可产生,因为在正域之间产生的差别矩阵的元素是对称的,故条件属性频率为2N1。
posiposj,任意两个划分集合都可产生,因为在正域之间产生的差别矩阵的元素是对称的,故条件属性频率为2N1。
2)若一个对象在Upos中,另一个对象在Uneg中,由划分的定义知,同属一个集合里的两个对象值相等,即只有不同划分集合里才有可能产生条件属性频率,且Upos和Uneg之间要求决策值不同,故需要对每个划分集合里属于Upos的集合对D划分,同时属于Uneg的集合也对D划分。所以,Negj/D划分集合里每个集合与posi/D划分集合里对于决策属性在不同划分集合里就能产生条件属性频率。
为了方便叙述,假设将Ai{b}所有集合中属于正域的所有集合对D划分posi/D存放在一个矩阵中,矩阵的行表示每一个非空集合对D的划分,矩阵的列表示决策值相同的集合,生成的矩阵为

同理,将Ai{b}所有集合中属于负域的所有集合对D划分 Negj/D存放在另一个矩阵中,生成的矩阵为

从这两个矩阵中可以看出,$\bar D$ij
只能与式(4)矩阵中与其不同行不同列的集合产生条件属性频率,为了求得所有条件属性频率且不重复计算,在式(4)矩阵中,定义任一行的和,即Si=|posi/D|= Dij|=|posi|,则所有行的总和
Dij|=|posi|,则所有行的总和 Si。
Si。
定义任一列的和:Tj= Dij。
Dij。
则若两个对象一个在
Upos中,另一个在Uneg中,产生的条件属性频率
N2=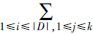 $\bar D$(S-Si-Tj+Dij)。故
FB(U,a)=
$\bar D$(S-Si-Tj+Dij)。故
FB(U,a)=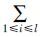 (2N1+N2)表示简化决策表中所有对象相对于条件属性集B产生的条件属性频率的总个数,证明完毕。
(2N1+N2)表示简化决策表中所有对象相对于条件属性集B产生的条件属性频率的总个数,证明完毕。
根据定义6可知,只有属性值不同且不为缺省值的才能包含条件属性,所以在本文的所有算法中,对象 U对属性a的划分,将含有缺省值的放在划分的最后一个集合里,不予处理。
4 属性约简算法首先,对不完备决策系统中的对象进行划分。
算法1 论域U对属性a的划分
输入 不完备决策表S=(U,C,D,V,f),C={a1,a2,…,am},U={x1,x2,…,x|U|}
输出 U/a={A1,A2,…,At}
1)t=1;At={xi};
2)for(j=2;j<|U|+1;j++)。
若任一条件属性ai∈C(i=1,2,…,|C|) 均有f(xi,ai)=f(xj,ai)≠*,则At=At∪{xj};否则t=t+1;At={xj};(其中在此求划分时*单独放到一块)。
3)输出U/a={A1,A2,…,At}。
算法1中,1)、3)时间复杂度忽略不计,2)的时间复杂度为O(|U|),则算法2的时间复杂度是 O(|U|),空间复杂度为O(|U|)。
算法2 求条件属性频率的函数
输入 U/A={A1,A2,…,At},条件属性的最大值和最小值分别标记为Mb,mb;
输出 U/(A∪{b}),条件属性频率函数|Fa(U,b)|;
1)|FA(U,b)|=0,U/(A∪{b})=∅;
2)对∀Ai={x1,x2,…,xj}∈U/A,以静态链表为存储空间,依次放入对象x1,x2,…,xj;令表头指针指向xi;
①建立Mb-mb+2空队列,令front[k]和end[k](k=0,1,2,…,Mb-mb+1)分别为第k个队列的头指针和尾指针,将链表中的对象x∈Ai按链表中的次序分配到第f(x,b)-mb个队列中去,将链表中的对象值为*的对象分配到*队列中。
②对除*队列的每个非空队列作如下处理:
a)将非空队列中属于Upos的对象放入
posi(i=0,1,2,…,k)中,属于Uneg的对象放入Negi(i=1,2,…,k)中。并计算两个对象都在U
pos中产生的条件属性频率N1,则N1=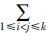 posiposj。
posiposj。
b)计算每个非空队列中posj/D=
{Dj1,Dj2,…,Dj|D|},
Negj/D={Dj1,Dj2,…,Dj|D|},则在正域矩阵中Si=|posi/D|= Dij|,S=
Dij|,S= Si所有集合中属于正域的所有集合对D划分posj/D中决策值相同集合总数为Tj=
Si所有集合中属于正域的所有集合对D划分posj/D中决策值相同集合总数为Tj= Dij。一个对象在Upos中,一个在Uneg中,产生的条件属性总频率为N2=
Dij。一个对象在Upos中,一个在Uneg中,产生的条件属性总频率为N2=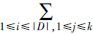 $\bar D$ij(S-Si-Tj+Dij)
,产生的条件属性总频率为|FA(U,b)|=2N1+N2;
$\bar D$ij(S-Si-Tj+Dij)
,产生的条件属性总频率为|FA(U,b)|=2N1+N2;
3)输出U/(A∪{b}),条件属性总频率数|FA(U,b)|。
算法时间空间复杂度分析:算法2中1)的时间复杂度忽略不计,2)①的时间复杂度为O(|Ai|),设posi/{b}={Ai1,Ai2,…,Aik},则2)②a时间复杂度为O(Aij)(j=1,2,…,k),2)②b时间复杂度为O(Aij),即2)②时间复杂度为 O(|Ai|),2)时间复杂度 O(|Ai|)+O(|A2|)+…+O(|Ai|)≤O(|U|)。故算法2的最坏时间复杂度为O(|U|),同理可得最坏空间复杂度为O(|U|)。
算法3 以条件属性的频率为启发信息的属性约简算法
输入 不完备决策表S=(U,C,D,V,f),C=(c1,c2,…,cm),U={x1,x2,…,xn};
输出 属性约简Red(C)。
1)由文献[11]求出容差类Tci(xi)(xi∈U),
Upos,Uneg计算知识粒度|GD(ci)|= |Tci(xi)|/|U|2,令|Ki|=GD(ci);
|Tci(xi)|/|U|2,令|Ki|=GD(ci);
2)将Ki按从小到大运用快速排序方法得到 |Ki1|≤ |Ki2|≤…≤|Kim|,它们对应的属性为 ci1,ci2,…,cim令 Red(C)={ci1};
3)for(k=2,k <m+1;k++)
由算法3计算;|Fred(U,ci(k-1))|
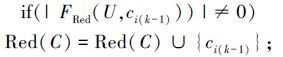
4)输出属性约简Red(C)。
算法正确性分析:若|FRed(U,ci(k-1))|=0,即当前属性不能将两个对象区分开,则RRed∪{cik}=RRed,则由算法3知,当输出约简 Red(C) 时,有RC=RRed。由定理2知,算法3求出的属性约简就是基于知识粒度的属性约简。
算法时间复杂度分析:算法3的1)由文献[11]知时间复杂度为 O(K|C||U|)(其中K=max{|Tc(xi)|,xi∈U}),空间复杂度为O(|U|)。2) 的时间复杂度为O(|C|)+O(|U|),空间复杂度为 O(|U|)(由算法1的复杂度分析可得)。3)的时间复杂度为O(|C||U|),空间复杂度为O(|U|)。故算法3的时间复杂度为O(K|C||U|)(其中K=max{|TC(xi)|,xi∈U},空间复杂度为O(|U|)。
5 实例分析为了证明算法的可行性,以文献[16]中的不完备决策表 1为例子进行相应说明。
| car | price | mileage | size | max-speed | conclusion |
| x1 | high | high | full | low | good |
| x2 | low | * | full | low | good |
| x3 | * | * | compact | high | poor |
| x4 | high | * | full | high | good |
| x5 | * | * | full | high | excel |
| x6 | low | high | full | * | good |
为方便计算,将属性值从左至右简记为 P、M、S、X,则该表的条件属性为C={P,M,S,X}。
由算法3 1)求得各属性的知识粒度分别是 :
|K1|=GD(P)=(4+4+6+4+6+4)/36=28/36;
|K2|=GD(M)=(6+6+6+6+6+6)/36=36/36;
|K3|=GD(S)=(5+5+5+5+5+1)/36=26/36;
|K3|=GD(X)=(3+3+4+4+4+6)/36=24/36;
Upos={x1,x2,x3},Uneg={x4,x5,x6}
由2)排序|K4|≤|K3|≤|K1|≤|K2|,他们对应的属性为X、S、P、M,则有Red(C)={X},RC=∅。
由3)计算|F∅(U,X)|=6,计算的|FX(U,S)|=6,计算的|F {X,S}(U,P)|=1,计算的|F{X,S,P}{U,M}|=0,算法结束,输出约简Red(C)={X,S,P}。
由算法2求|FRed(X)|。
输入 U/∅={x1,x2,x3,x4,x5,x6}
由算法2,2)的2)①对 A1={x1,x2,x3,x4,x5,x6}求得:
front[*]→x6→end[*];
对第1个非空队列有pos1={x1,x2},Neg1= ∅;
对第2个非空队列pos2={x3},Neg2={x4,x5},则
N1=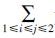 posiposj=
|pos1|*|pos2|=2*1=2。
posiposj=
|pos1|*|pos2|=2*1=2。
由算法2,2)的②计算每个非空队列中的posi/D。
D11={x1,x2},D12=∅,D13=∅,
D21=∅,D22={x3},D23=∅ ,则
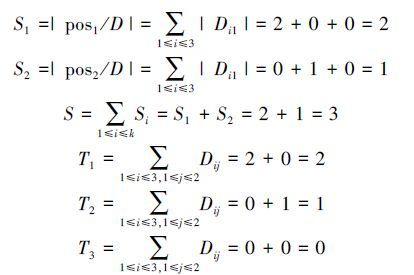
每个非空队列中的Negi/D:

对A*={x6},因A*不能区分对象,故无需计算。
故|F∅(U,X)|=2N1+N2=2*2+2=6,
求|FX(U,S)|。
输入 U/(X)={{x1,x2},{x3,x4,x5}}
由算法2 2)的①对A1={x1,x2}求得front[1]→x1→x2→end[1];
对其划分有pos1={x1,x2},Neg1=∅;
易知,|FX(U,S)|1=0,
对A2={x3,x4,x5}求得
对第1个非空队列有pos1={x3},Neg1=∅;
对第2个非空队列pos2=∅,Neg2={x4,x5},
则N1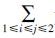 posiposj=1*0=0,对决
策属性划分后得
posiposj=1*0=0,对决
策属性划分后得
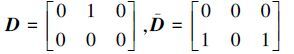
|FX(U,S)|2=2N1+N2=0+6=6
|FX(U,S)|=|FX(U,S)|1+|FX(U,S)|2=6
输入 U/(X∪({S})={{x1,x2},{x3},{x4,x5} 由算法2的2)①对 A1={x1,x2}求得
对第1个非空队列有 pos1={x1},Neg1=∅;
对第2个非空队列pos2={x2},Neg2=∅。
则
N1=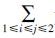 posiposj=1*1=1易知N2=0,
posiposj=1*1=1易知N2=0,
故|F{X,S}(U,P)|1=1。
对A2={x3} 求
易知,|F{X,S}(U,P)|2=0
对A3={x4,x5}求得
front[*]→x5→end[*];
易知,|F{X,S}(U,P)|3=0,
|F{X,S}(U,P)|=|F{X,S}(U,P)|1+
|F{X,S}(U,P)|2+|F{X,S}(U,P)|3=1
输入 U/({X,S}∪{P})={{x1},{x2},{x4}}
求得|F{X,S,P}(U,M)|=0。
实例说明,该约简与文献[5]相同。新算法不仅通俗易懂,且在粒度差别矩阵的基础上大大减少存储空间,且大大提高了算法收敛的时间速度,即新算法是一个高效可行的属性约简算法。
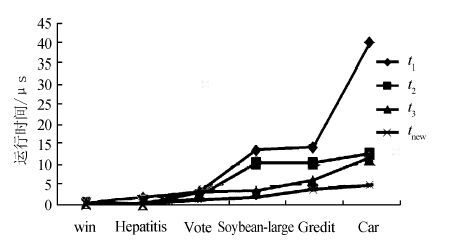
6 实验对比为了更好地说明新算法比其他同类算法更具有有效性和实用性,选用UCI机器学习数据库中的6个数据集:Credit、Car、Hepatitis、Soybean-large、Vote和Wine进行实验。选取比较新的算法进行对比,考察新算法的高效性,分别与文献[17]、文献[18]、文献[11]进行对比,文献[17]是在差别矩阵的基础上提出的属性约简算法,文献[17]算法运行时间记为 t1,文献[18]是基于冲突域的属性约简算法,算法运行时间记为t2,文献[11] 算法运行时间 记为t3,本文算法运行时间记为tnew,对比结果见表 2。为了增强实验结果的可靠性,本文所取的最终时间为 7次实验结果的平均值。实验运行的环境为:CPU为AMD,2.00 GB内存,在Visual Stdio2010平台。
| 数据集 | 完备 | |C| | |U| |
| Car | 是 | 6 | 1 700 |
| Hepatitis | 否 | 15 | 199 |
| Vote | 否 | 16 | 435 |
| Credit | 否 | 15 | 690 |
| Soybean-large | 否 | 35 | 351 |
| Wine | 是 | 14 | 178 |
|
| 图 1 UCI数据集对比 Fig. 1 The comparison of UCI data sets |
表 2中的数据集,|C|代表条件属性个数,|U|代表对象个数。
从表 2 中的实验数据可以看出,对于小的数据集({Hepatitis,15,199},{Wine,14,178})上,对比的4种算法的运行时间相差不大。但是对于较大的数据集,运行时间就相差很大,而且随着数据集的扩大,新算法的运行时间相对于其他3种算法的增长幅度小得多,表明新算法具有较好的可扩展性。
7 结束语在决策表中,知识粒度是有效进行属性约简的方法,以往的属性约简算法由于计算知识粒度浪费了大量时间,算法效率不高。因此,本文设计一个基于知识粒度的计算条件属性频率的启发函数,以知识粒度为启发信息,提出新的属性约简算法,大大降低了算法的时间复杂度。在以后的研究中,可以将计算属性频率的思想利用到其他属性约简的方法中,如相容矩阵、差别矩阵等,也可进一步应用到规则获取中。
| [1] | PAWLAK Z, GRZYMALA-BUSSE J, SLOWINSKI R. Rough sets[J]. Communications of the ACM, 1995, 8(1):89-95. |
| [2] | PAWLAK Z. Rough set theory and its applications to data analysis[J]. Cybernetics and systems:an international, 1998, 29(7):661-668. |
| [3] | KRYSZKIEWICZ M. Rough set approach to incomplete information systems[J]. Information sciences, 1998, 112(1-4):39-49. |
| [4] | 钱文彬, 杨炳儒, 徐章艳, 等. 基于不完备决策表的容差类高效求解算法[J]. 小型微型计算机系统, 2013, 34(2):345-350. QIAN Wenbin, YANG Bingru, XU Zhangyan, et al. Efficient algorithm for computing tolerance classes of incomplete decision table[J]. Journal of Chinese computer systems, 2013, 34(2):345-350. |
| [5] | 李秀红, 史开泉. 一种基于知识粒度的不完备信息系统的属性约简算法[J]. 计算机科学, 2006, 33(11):169-170, 199. LI Xiuhong, SHI Kaiquan. A knowledge granulation-based algorithm for attribute reduction under incomplete information systems[J]. Computer science, 2006, 33(11):169-170, 199. |
| [6] | 史先红, 史进玲. 一种基于相对粒度的不完备决策表约简算法[J]. 河南师范大学学报:自然科学版, 2010, 38(4):51-53, 84. SHI Xianhong, SHI Jinling. A reduction algorithm based on relative granularity in incomplete decision tables[J]. Journal of Henan normal university:natural science, 2010, 38(4):51-53, 84. |
| [7] | 张清国, 郑雪峰. 基于知识粒度的不完备决策表的属性约简的矩阵算法[J]. 计算机科学, 2012, 39(2):209-211, 243. ZHANG Qingguo, ZHENG Xuefeng. Discernibility matrix algorithm of attribute reduction based on knowledge granulaion in incomplete decision table[J]. Computer science, 2012, 39(2):209-211, 243. |
| [8] | 张伟, 徐章艳, 王晓宇. 一种结合概率启发信息和知识粒度的属性约简算法[J]. 计算机应用与软件, 2013, 30(7):43-45, 50.ZHANG Wei, XU Zhangyan, WANG Xiaoyu. An attribute reduction algorithm combining probability heuristic information and knowledge granularity[J]. Computer applications and software, 2013, 30(7):43-45, 50. |
| [9] | PAWLAK Z. Rough sets and intelligent data analysis[J]. Information sciences, 2002, 147(1-4):1-12. |
| [10] | 王炜, 徐章艳, 李晓瑜. 不完备决策表中基于对象矩阵属性约简算法[J]. 计算机科学, 2012, 39(4):201-204. WANG Wei, XU Zhangyan, LI Xiaoyu. Attribute reduction algorithm based on object matrix in incomplete decision table[J]. Computer science, 2012, 39(4):201-204. |
| [11] | 舒文豪, 徐章艳, 钱文彬, 等. 一种快速的不完备决策表属性约简算法[J]. 小型微型计算机系统, 2011, 32(9):1867-1871. SHU Wenhao, XU Zhangyan, QIAN Wenbin, et al. Quick attribution reduction algorithm based on incomplete decision table[J]. Journal of Chinese computer systems, 2011, 32(9):1867-1871. |
| [12] | 韩智东, 王志良, 高静. 用差别矩阵思想设计的基于正区域的高效属性约简算法[J]. 小型微型计算机系统, 2011, 32(2):299-304.HAN Zhidong, WANG Zhiliang, GAO Jing. Efficient attribute reduction algorithm based on the idea of discernibility object pair set[J]. Journal of Chinese computer systems, 2011, 32(2):299-304. |
| [13] | 钟珞, 梅磊, 郭翠翠, 等. 粒矩阵属性约简的启发式算法[J]. 小型微型计算机系统, 2011, 32(3):516-520. ZHONG Luo, MEI Lei, GUO Cuicui, et al. Heuristic algorithm for attribute reduction on granular matrix[J]. Journal of Chinese computer systems, 2011, 32(3):516-520. |
| [14] | 唐孝, 舒兰. 基于粒计算的属性约简改进算法[J]. 计算机科学, 2014, 41(11A):313-315, 346. TANG Xiao, SHU Lan. Improved algorithm of attribute reduction based on granular computing[J]. Computer science, 2014, 41(11A):313-315, 346. |
| [15] | 张清国, 郑雪峰. 相容矩阵的高效属性约简算法[J]. 小型微型计算机系统, 2012, 33(9):1944-1947. ZHANG Qingguo, ZHENG Xuefeng. An efficiency attribute reduction algorithm of tolerance matrix[J]. Journal of Chiese computer systems, 2012, 33(9):1944-1947. |
| [16] | 梁吉业, 李德玉. 信息系统中的不确定性与知识获取[M]. 北京:科学出版社, 2005:1-70. |
| [17] | 王炜, 徐章艳, 李晓瑜.不完备决策表中基于对象矩阵属性约简算法[J]. 计算机科学, 2012, 39(4):201-204.WANG Wei, XU Zhangyan, LI Xiaoyu. Attribute reduction algorithm based on object matrix in incomplete decision table[J]. Computer science, 2012, 39(4):201-204. |
| [18] | 周建华, 徐章艳, 章晨光. 一种基于冲突域的不完备决策表属性约简算法[J]. 计算机应用与软件, 2014, 31(3):239-241, 255. ZHOU Jianhua, XU Zhangyan, ZHANG Chenguang. An incomplete decision table attribute reduction algorithm based on conflict region[J]. Computer applications and software, 2014, 31(3):239-241, 255. |



