冠心病是供应心脏的血管冠状动脉发生硬化狭窄疾病的简称,以冠状动脉粥样硬化性狭窄多见。冠状动脉造影是诊断冠心病的一个“金标准”,诊断地位非常高。如果血管轮廓光滑,没有狭窄缺损的表现,那就没有冠心病;如果见到狭窄表现,那就是冠心病。实际上获得的造影图像经常是不理想的,影响了医生对病人病情的诊断,因此对冠脉造影图像进行有效的增强对辅助医生诊断有着很重要的作用。近年来,不少学者致力于研究血管增强的算法,也取得了相当多的研究成果和方法。其中一种被广泛应用的是基于Hessian矩阵的血管增强方法,如Frangi的方法[1, 2, 3]、Sato的方法[4]、Lorenz的方法[5]、Krissian的方法[6, 7, 8]等。这种方法可被检测到的血管的宽度可以在一个很大的范围内,但是它存在着对医学诊断来说极其致命的缺点——分支处的不连续。Perona和Milik将各向异性扩散方程引入血管增强领域[9],将其代替高斯平滑滤波器。这种方法能够很好地增强血管结构,但是在求解偏微分方程时运算量非常大。针对冠脉造影图像中血管存在连续性、方向性和尺度渐变的特点,很多学者将方向滤波器组应用到血管增强中。本文结合无抽样方向滤波器组和Hessian矩阵对血管图像进行增强,提出了一种新的方向图像合成方法,将增强结果与其他的血管增强方法进行对比验证。
1 图像分解本文算法涉及到的一个很重要的步骤就是对造影图像进行方向分解。方向分解属于多尺度几何分析,能够充分利用数据本身所特有的几何特性。对图像进行方向分解需要使用方向滤波器组(directional filter banks,DFBs),DFB最初被Bamberger和Smith[10]提出,文献说明了DFB可以将输入图像的光谱区分解成n=2k(k=1,2,…)个楔形频率子带,每个子带与空间域的一个特定方向的线性特性相对应。起初DFB多被用于图像压缩[11],后来被用于图像增强[12, 13],在文献[14]中,DFB被用于指纹识别。方向滤波器组可以将一个图像分解为最大幅度抽样的波带,每个波带对应一个单独的角度,并且可以通过一个双合成滤波器完美地重构图像。方向滤波器的输出被称为波带。文献[10]表明,使用方向滤波器组分解图像得到的输出波带在空间域上的显示是扭曲的,它们由于混淆而视觉失真了。
方向滤波器组有着一定的缺点,即次波带的大小比原始图像要小。波带大小上的缩小是由于抽样。当方向滤波器组被用于图像分解时,抽样的操作造成了2个问题:一是随着方向分辨率的增加,空间分辨率会降低;另外一个是该方法涉及到一个额外的插值过程,这个额外的插值过程不仅影响整个系统的效率,而且会产生错误的噪声,它对医学图像来说是尤其有害的。由于这些噪声的存在,一些血管可能被破坏,一些血管可能被错误地连接到其他血管。因此,一个可能的研究方向是修改方向滤波器组的结构,使分解过程中没有抽样操作。本文采用将抽样和重采样部分转移到滤波器的左侧的方法来建一个无抽样方向滤波器组(decimation-free directional filter banks,DDFBs),它最后得到的不是方向波带,而是方向图像,达到了消除插值的目的。
8方向的DFBs需要3层结构。第1层的结构需要一组菱形通带滤波器组
H0ω1,ω2,H1ω1,ω2,一个调节器和不可分的梅花型2×2下采样矩阵
: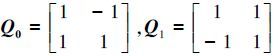 式中:
式中: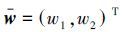 是一组二维傅里叶频率变量。在这一层中,首先使用调节器通过π改变输入图像的频谱,在经过调节器处理之后,组成的频率成份发生了变化。然后使用菱形滤波器,对两种频率区域进行滤波。每个滤波器后都伴随着一个梅花形下采样矩阵。该矩阵不仅对图像进行下采样,而且能够将图像旋转45°。DFBs第2层所需要的结构和第1层相同。第1层输出的波带作为这一层的输入。第2层产生的波带的光谱几何结构有一个平行四边形的几何结构。方向滤波器组的第3层结构与第1层、第2层相比,增加了重采样矩阵和后采样矩阵。重采样矩阵Ri被用于将平行四边形波带变为菱形波带。后采样矩阵将所有的非对角的采样矩阵转变为菱形的。得到的每个波带图像比原始图像要小,因此所有波带的像素之和与原始图像的像素个数是相
同的。
是一组二维傅里叶频率变量。在这一层中,首先使用调节器通过π改变输入图像的频谱,在经过调节器处理之后,组成的频率成份发生了变化。然后使用菱形滤波器,对两种频率区域进行滤波。每个滤波器后都伴随着一个梅花形下采样矩阵。该矩阵不仅对图像进行下采样,而且能够将图像旋转45°。DFBs第2层所需要的结构和第1层相同。第1层输出的波带作为这一层的输入。第2层产生的波带的光谱几何结构有一个平行四边形的几何结构。方向滤波器组的第3层结构与第1层、第2层相比,增加了重采样矩阵和后采样矩阵。重采样矩阵Ri被用于将平行四边形波带变为菱形波带。后采样矩阵将所有的非对角的采样矩阵转变为菱形的。得到的每个波带图像比原始图像要小,因此所有波带的像素之和与原始图像的像素个数是相
同的。
无抽样方向滤波器组(DDFB)是在方向滤波器组的基础上进行改进的。8方向DDFB的第1层结构只需要2个滤波器H00ω1,ω2,H11ω1,ω2。它包含沙漏形状的滤波通带,这个滤波通带是通过将 DFB第1层的调节器移动到滤波器左边得到的。因此DDFB与DFB第1层所使用的滤波器之间的关系可表示为
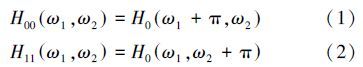
DDFB第2层所需要的滤波器是 H00 QTω1,ω2和H11QTω1,ω2 ,其中T代表转置, Q与DFB第1层中的梅花形下采样矩阵相同。DDFB第2层的滤波器与DFB中滤波器的关系可表示为

从DDFB第1层中得到的方向图像通过这两个滤波器进一步处理,所得到的图像在这一层不需要进一步处理。
DDFB第3层所需要的滤波器是 H00iω1,ω2和H11iω1,ω2,其中 i=1,2,3,4。这一层一共需要8个不同的滤波器。DDFB第三层的滤波器与DFB中滤波器的关系可表示为
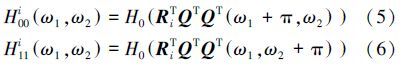
将原图像进行方向分解后,需要对方向图像的血管建立血管模型。假定在二维X射线造影图像中,血管在黑色的背景上是明亮的,并且亮度从中间到边界是逐渐降低的。那么由于血管的横截面灰度分布类似高斯曲线,因此可以表示为

上述模型的Hessian矩阵可表达如下:
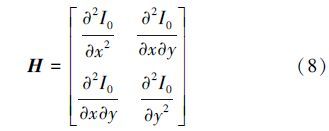
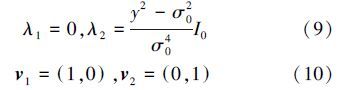
为了获得不同大小的血管,需要计算不同尺度 σ下的梯度和Hessian矩阵。通过与高斯卷积来计算导数:
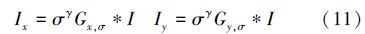
对血管中的像素点(y2<σ02 ),负的特征值对应的特征向量与血管方向正交。另一个特征值的绝对值更小,其对应的特征向量与血管轴的方向相同。在这种情况下,当血管方向v1与x轴方向相同时,Hessian的特征值与它对角线上的值相同。利用这个特征来计算Hessian矩阵的特征值,得到了与原始方法相比对噪声更加不敏感的计算方法。
为了在计算特征值时减少噪声的影响,在建模时让血管方向与x轴方向一致。实现这个思想的一个可行的方法是旋转方向图像,然而图像旋转需要插值,这样很有可能产生噪声,对医学图像的处理是很有害的,因此通过旋转坐标系实现。
假设方向图像Iii=1,2,…,n对应方向从θi,min到θi,max (逆时针方向旋转)。则相关联的坐标系Oxy将被旋转到Ox′y′,旋转的角度为 θi=θi,min+θi,max/2。
方向图像Ii的海森矩阵在新坐标系中的定义为
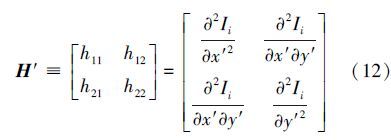
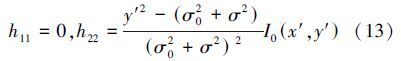
实际上,一般来说血管轴并非与x轴完全一致,因此h11≈0。在血管中,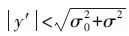 ,因此h22是负的。所以,当h22<0且
,因此h22是负的。所以,当h22<0且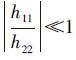 时,血管像素点得以确定。
时,血管像素点得以确定。
在传统的基于方向滤波器组的图像处理中,合成时采用的是将各方向图像直接相加的方式进行合成,从而得到最后的图像处理结果。设每一个方向图像为
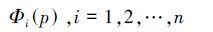
传统的重构得到最后图像的方法如下:
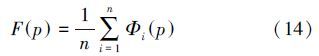
一种常用的图像加权方法是高斯加权。高斯加权中一个点邻域内某像素的权值为该像素与中心像素灰度差的高斯函数,可以根据不同方向邻域点的权值确定方向图像的权值。
针对冠脉造影图像中血管存在方向性的特点,提出一种方向加权的方法,增加主方向图像像素点的权重,从而能够更准确地捕捉到血管的信息,减少干扰像素点在加权平均计算时的权值。
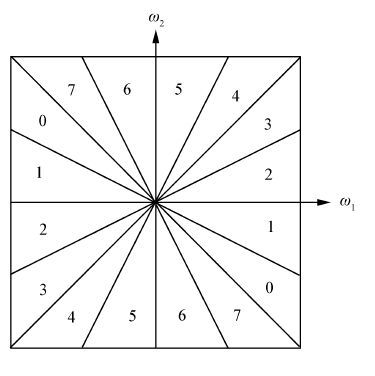
加权合成时,需要确定主方向,根据图像计算梯度,根据不同方向梯度的大小来采用不同的方向权值进行加权。如图 1所示,对于8方向分解,计算每个方向的中心梯度来确定各自的权值。由于每个方向图像确定的方向是一个范围,采用每个方向中心的梯度来确定该方向的权值。由于方向分解的方向并非平均的角度,因此要确定这些梯度所需要的邻域是非常大的,而邻域取过大不利于确定该点附近各方向的信息,因此最终取各方向两边缘的均值来确定该方向的权值。为了计算8方向的方向梯度,以每个像素点为中心选取5×5的邻域。
|
| 图 1 方向分解示意图 Fig. 1 Direction decomposition diagram |
由于图像在计算机中以数字图像的形式进行存储,即图像是离散的数字信号,因此对数字图像的梯度使用差分来代替连续信号中的微分。对于图像f(i,j),在点(i,j)处沿x方向和y方向的一阶差分可以表示为
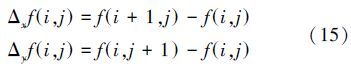
同理,利用差分方程对x和y方向上的二阶偏导数进行近似为
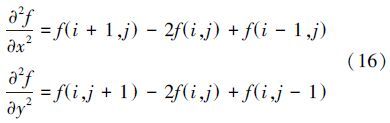
水平垂直以及45°倍数方向仍然用3×3邻域的像素点插值计算。
设中心像素点为f(i,j),按上述方法可以计算得到8个方向的梯度如下:
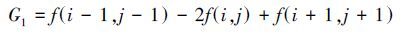
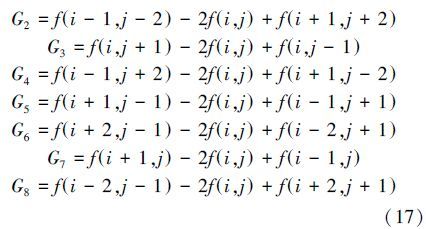
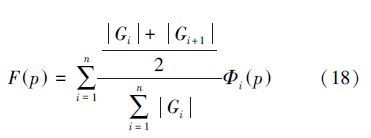
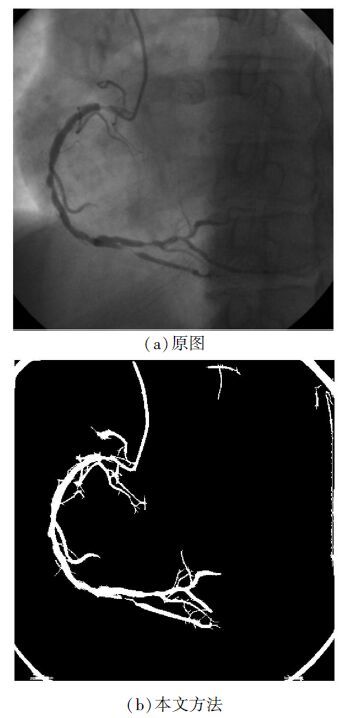
利用大连医科大学第二附属医院提供的冠脉造影图像,使用本文中所描述的方法,对冠脉造影图像进行血管增强,得到的结果如图 2所示。
|
| 图 2 血管增强结果 Fig. 2 Vascular enhancement result |
将本文算法的血管提取结果与现有的基于Hessian矩阵的血管增强算法结果作比较。
图 3给出了传统的基于Hessian矩阵的血管图像增强[1]和本文提出的基于无抽样方向滤波器组的图像增强算法的实验结果对比。可以明显地看出,基于Hessian矩阵的图像增强方法得到的结果在血管连接处有明显的断开,且不能显示小血管;而本文算法得到的结果相对较好,增强效果明显,细节部分清晰,可以正确地显示小而薄的血管,有效地避免了结抑制,从而能够得到连续的血管树。

|
| 图 3 不同算法的结果 Fig. 3 The results of different algorithms |
本文从血管图像的特点出发,结合无抽样方向滤波器组和Hessian增强对血管进行增强,提出一种基于方向梯度的方向图像加权合成方法,并且应用于冠脉造影图像。本文方法的优点是能够较好地提取分支和交叉处的血管,能够获得不同的方向图像,因此可以得到不同的区别于原始图像的Hessian特征值。方向图像的数量越大,结果就越准确,但是时间代价也会更高。如何在保证结果准确的基础上降低时间代价是进一步研究的方向。
| [1] | FRANGI A F, NIESSEN W J, VINCKEN K L, et al. Multiscale vessel enhancement filtering[M]//WELLS W M, COLCHESTER A, DELP S L. Medical Image Computing and Computer-Assisted Interventation-MICCAI'98. Berlin Heidelberg:Springer, 1998:130-137. |
| [2] | FRANGI A F, NIESSEN W J, HOOGEVEEN R M, et al. Model-based quantitation of 3-D magnetic resonance angiographic images[J]. IEEE transactions on medical imaging, 1999, 18(10):946-956. |
| [3] | FRANGI A F, NIESSEN W J, NEDERKOORN P J, et al. Quantitative analysis of vascular morphology from 3D MR angiograms:In vitro and in vivo results[J]. Magnetic resonance in medicine, 2001, 45(2):311-322. |
| [4] | SATO Y, NAKAJIMA S, SHIRAGA N, et al. Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images[J]. Medical image analysis, 1998, 2(2):143-168. |
| [5] | LORENZ C, CARLSEN I C, Buzug T M, et al. A multi-scale line filter with automatic scale selection based on the Hessian matrix for medical image segmentation[M]//TER HAAR ROMENY B, FLORACK L, KOENDERINK J, et al. Scale-Space Theory in Computer Vision. Berlin Heidelberg:Springer, 2006, 1252:152-163. |
| [6] | KRISSIAN K. Flux-based anisotropic diffusion applied to enhancement of 3D angiograms[J]. IEEE transactions on medical imaging, 2002, 21(11):1440-1442. |
| [7] | KRISSIAN K, MALANDAIN G, AYACHE N. Directional anisotropic diffusion applied to segmentation of vessels in 3D images[M]//TER HAAR ROMENY B, FLORACK L, KOENDERINK J, et al. Scale-Space Theory in Computer Vision. Berlin Heidelberg:Springer, 1997, 1252:345-348. |
| [8] | KRISSIAN K, MALANDAIN G, AYACHE N, et al. Model-based detection of tubular structures in 3D images[J]. Computer vision and image understanding, 2000, 80(2):130-171. |
| [9] | PERONA P, MALIK J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE transactions on pattern analysis and machine intelligence, 1990, 12(7):629-639. |
| [10] | BAMBERGER R H, SMITH M J T. A filter bank for the directional decomposition of images:theory and design[J]. IEEE transactions on signal processing, 1992, 40(4):882-893. |
| [11] | BAMBERGER R H. New subband decompositions and coders for image and video compression[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. San Francisco, CA, 1992:217-220. |
| [12] | PARK S, SMITH M J T, LEE J J. Fingerprint enhancement based on the directional filter bank[C]//Proceedings of International Conference on Image Processing. Vancouver, BC, 2000, 3:793-796. |
| [13] | BAMBERGER R H. New results on two and three dimensional directional filter banks[C]//Proceedings of the Twenty-Seventh Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, 1993, 2:1286-1290. |
| [14] | PARK C H, LEE J J, SMITH M J T, et al. Directional filter bank-based fingerprint feature extraction and matching[J]. IEEE transactions on circuits and systems for video technology, 2004, 14(1):74-85. |
| [15] | FLORACK L M J, TER HAAR ROMENY B M, KOENDERINK J J, et al. Scale and the differential structure of images[J]. Image and vision computing, 1992, 10(6):376-388. |
| [16] | LINDEBERG T. Edge detection and ridge detection with automatic scale selection[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, CA, 1996:465-470. |



