复杂系统[1, 2, 3, 4]中存在着各种各样的关系,相关性是其中最重要的一种关系。由于相关性的存在,当对系统中的某个对象实施主动可拓变换时,会导致与其相关的其他对象发生传导变换[5]。尤其当其中存在的矛盾问题需要解决时,更要关注相关性和传导变换[6, 7, 8, 9, 10]。例如,一项复杂的产品往往是由很多个部分连接组装而成,各个部分之间以及它们与整个产品的属性之间必然存在着纷繁交错的依赖关系。在复杂产品的创新设计中,如果对某一部分的结构和材质实施变换,则其他相关的部分也会随之改变,进而引起整个产品的功能和成本等发生传导变换。为此,设计者需要对这一传导过程中所涉及的传导机制有清晰、准确的认识,才能有效地提升产品的功能、降低成本。由此可见,研究传导变换的相关理论和计算模型具有非常重要的意义。
相关性是传导变换产生的根源,事物之间的相关关系决定了传导变换的对象和效应。文献[11, 12, 13, 14, 15]基于基元的相关性介绍了传导变换的概念以及传导效应的计算方法。然而,这些研究都是在基元相关链、基元相关环和基元相关树等规则的基元相关关系下进行的。对于大部分的系统而言,其内部事物之间的相关关系实质上是一个包含多个不规则基元相关关系的复杂基元相关网,基于此的传导变换过程非常复杂,需要综合多方面的信息,往往不是人脑能够勾划的,必须利用计算机来实现。这就需要建立基于不规则基元相关关系的传导变换理论以及相应的形式化表达模型。为此,本文提出了基元相关矩阵和基元相关函数的概念,建立了复杂基元相关网下的传导推理规则和传导效应计算模型,并结合实例进行说明。
1 基元相关矩阵和基元相关函数 1.1 基元相关矩阵在基元相关网中,不同基元之间的相关关系错综复杂,为了直观、形式化地表达这些相关关系,本文提出基元相关矩阵的概念。
定义1 (单评价特征基元相关矩阵) 设给定基元集合B1,B2,…Bn和评价特征c,定义基元相关矩阵 ρ如下:


ρij=1;否则ρij=0。若ρji>=ρij=1,则表示基元Bi和Bj关于评价特征c互为相关,记作

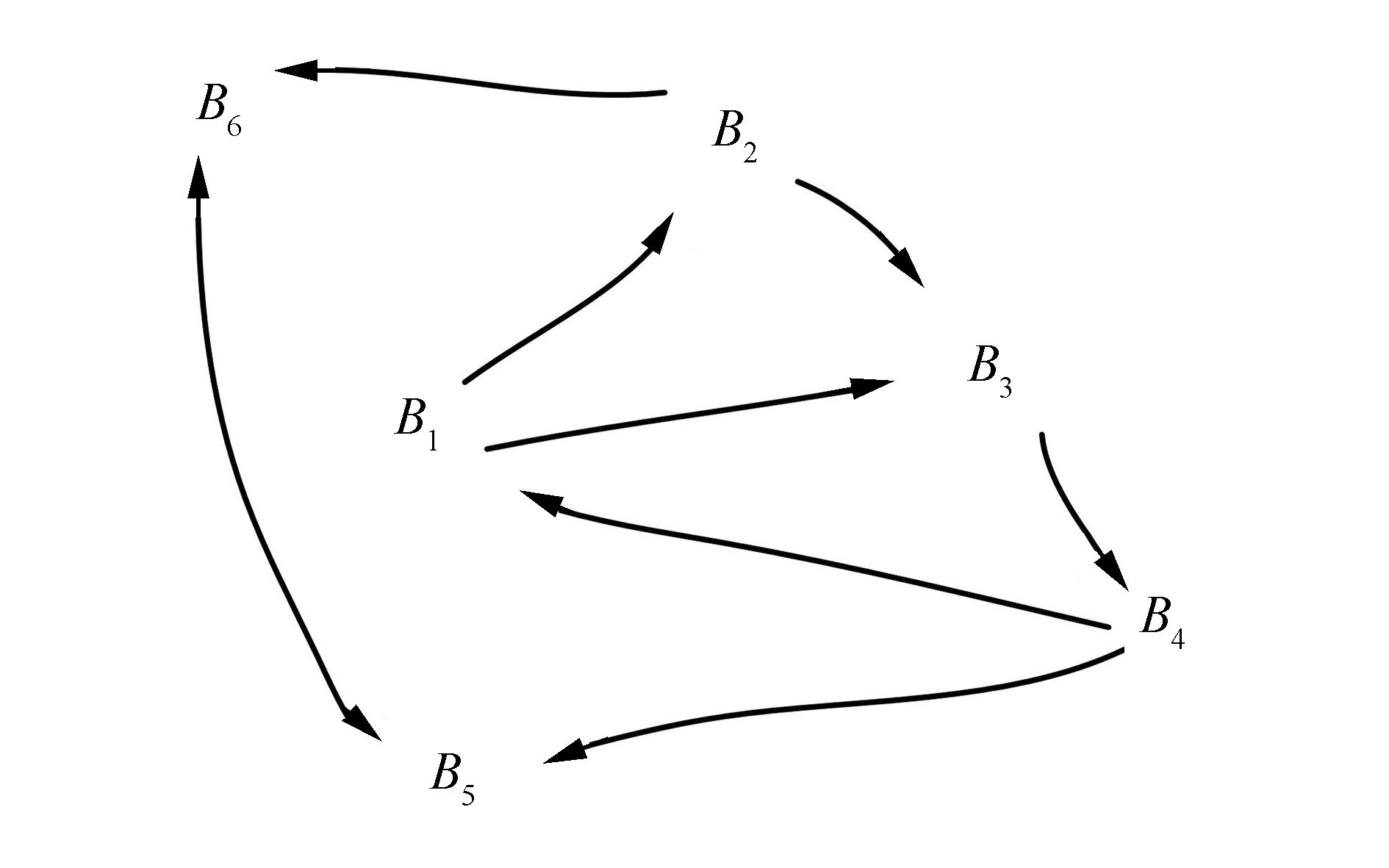
例如,给定6个基元之间关于评价特征c的相关关系如图 1所示。
|
| 图 1 6个基元的相关关系 Fig. 1 Correlations of the six basic-elements |
定义2(多评价特征基元相关矩阵) 对于给定基元集合B1,B2,…,Bn,设Bi的评价特征集合为Ci=ci1,ci2,…,cimi(mi为Bi评价特征的个数),定义分块基元相关矩阵ρ为
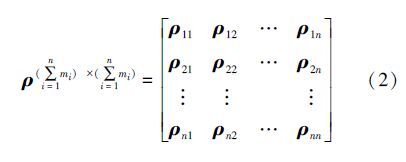
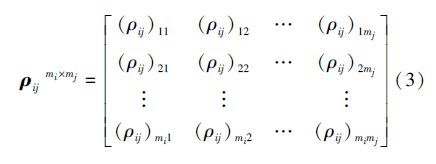
式中:(ρij)kl(1≤k≤mi,1≤l≤mj)的取值集合为0,1,若基元Bi关于评价特征cik和Bj关于评价特征cjl单向相关,即满足

基于基元相关矩阵,可以建立定量化表达基元相关关系的基元相关函数。
定义3(单评价特征基元相关函数) 设给定基元集合B1,B2,…,Bn,评价特征c和基元相关矩阵ρ,对于基元Bj,若i|ρij=1,i≠j=i1,i2,…,is非空,则根据相关性必有
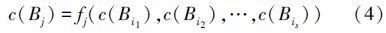
定义4(多评价特征基元相关函数) 对于给定基元集合B1,B2,…,Bn,相应的评价特征集合C1,C2,…,Cn以及分块基元相关矩阵ρ,对于基元Bj的第l个评价特征cjl,记

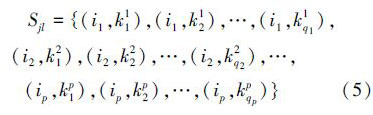
则根据相关性必有
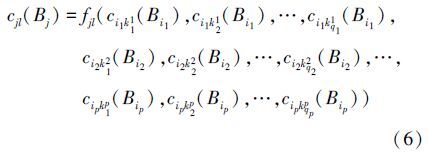
由以上内容可知,单评价特征相关可以作为多评价特征相关的特例来考虑。为此,本文仅考虑多评价特征相关下的传导规则。
对于基元相关网中的基元而言,在主动变换实施以后,某一基元可能由于局部相关环的作用而多次发生传导变换。为了准确地区分这些变换,这里引入基元变换阶的概念。
定义5 (基元变换阶) 设基元集{B1,B2,…,Bn}在主动变换的作用下发生了N(N为非负整数)次传导变换,称第k个基元被变换过的次数(包括主动变换)为该基元在N次传导变换下的变换阶,记为Qk(N)。
传导推理规则1对于可拓变换Ti=(Bi,Bi′),记Ti的一次传导变换集合为Ψ1(Ti),则

当j≠i时,Qj(0)=0,Qj(1)=1,Ti⇒φj=(Bj,Bj′)表示由不同对象之间的相关性引起的传导变换;当 j=i时,Qj(0)=1,Qj(1)=2,φj(2)=(Bj ′,Bj″)表示由相同对象关于不同评价特征的相关性引起的自身传导变换,故φ(2)j称为二阶变换。
传导推理规则2 记Ti的下标序集为U0 (Ti),若主动变换Ti涉及基元Bi的第k个特征,则 (i,k)∈U0(Ti)。基元集合B1,B2,…,Bn分块基元相关矩阵为ρ,则
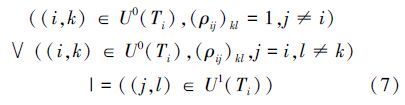
若j≠i,表示由不同对象之间的相关性引起的传导变换;若j=i,表示由相同对象关于不同评价特征的相关性引起的自身传导变换。
传导推理规则3 若Ti的二次传导变换集合为Ψ2(Ti),则

传导推理规则4 设U2(Ti)为Ti的二次传导变换的下标序集,则有
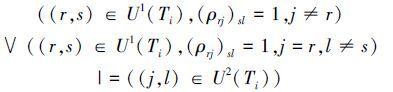
传导推理规则5 设Ti的N(N>2)次传导变换集合为ΨN(Ti),则
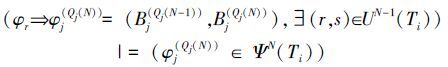
传导推理规则6 设UN(Ti)为Ti的N (N>2)次传导变换的下标序集,则有

传导效应是定量化评价传导变换的重要指标[12],文献[12]将传导变换关于某个评价特征的传导效应定义为基元关于该评价特征在变换前后的量值之差。对于连续、复杂的传导过程,希望利用先前的基元信息,对后续的传导效应进行计算。为此,本文利用基元相关函数给出复杂基元相关网下传导效应的计算模型。
原理1(一次传导变换效应) 设φ(Qj(1))j=(B(Qj(0))j,B(Qj(1))j)是Ti一次传导变换集合Ψ1(Ti)中的变换,即φ(Qj(1))j∈Ψ1(Ti),设Sjl非空,则根据定义4可知,φ (Qj(1))j关于评价特征cjl(1≤l≤mj)的一次传导效应为
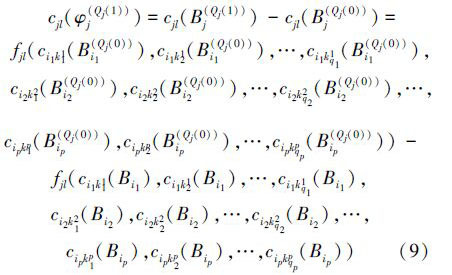
原理2(二次传导变换效应) 设φ(Qj(2))j=(B(Qj(1))j,B(Qj(2))j)是Ti二次传导变换集合Ψ2(Ti)中的变换,即φ(Qj(2))j∈Ψ2(Ti),设Sjl非空,则根据定义4可知,φ(Qj(2))j关于评价特征cjl(1≤l≤mj)的二次传导效应为

原理3(N(N>2)次传导变换效应) 设φ(Qj(N))j=(B(Qj(N-1))j,B(Qj(N))j)是Ti的N次传导变换集合ΨN(Ti)中的变换,即φ(Qj(N))j∈ΨN(Ti),设Sjl非空,则根据定义4可知,φ(Qj(N))j关于评价特征cjl(1≤l≤mj)的N次传导效应为
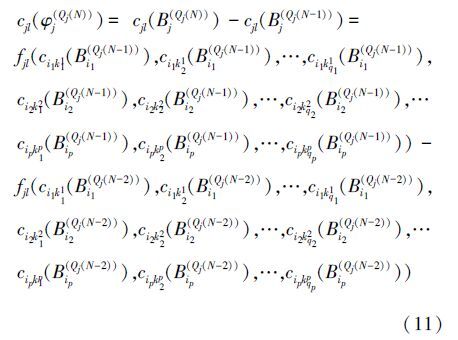
以某企业的产品供销活动为例,采用上述理论与方法,可以用形式化的方法建立由产品、消费者和生产企业构成的供销系统中的相关关系,并建立当主动变换为产品的材质和结构时,相应的传导规则和传导效应计算模型。
首先将产品、消费者和生产企业用物元来表达:
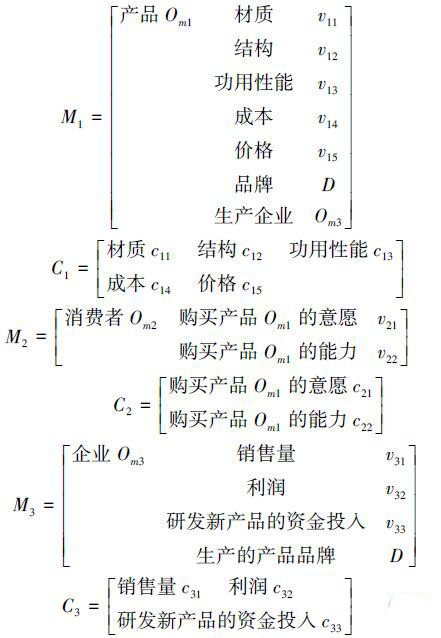
由供销活动的相关领域知识可知,M1、M2和M3的相关关系如下:
产品的材质与产品的功用性能相关:
(c11)M1 (c13)M1;
(c13)M1;
产品的结构与产品的功用性能相关:
(c12)M1 (c13)M1;
(c13)M1;
产品的材质与产品的成本相关:
(c11)M1 (c14)M1;
(c14)M1;
产品的结构与产品的成本相关:
(c12)M1 (c14)M1;
(c14)M1;
产品的成本与产品的价格相关:
(c14)M1 (c15)M1;
(c15)M1;
产品的功用性能与消费者购买产品的意愿相关:
(c13)M1 (c21)M2;
(c21)M2;
产品的价格与消费者购买产品的意愿相关:
(c15)M1 (c21)M2;
(c21)M2;
消费者购买产品的能力与消费者购买产品的意愿相关:
(c22)M2 (c21)M2
(c21)M2
消费者购买产品的意愿与生产企业的销售量相关:
(c21)M2 (c31)M3;
(c31)M3;
生产企业的销售量与生产企业的利润相关:
(c31)M3 (c32)M3;
(c32)M3;
产品的成本与生产企业的利润相关:
(c14)M1 (c32)M3;
(c32)M3;
产品的价格与生产企业的利润相关:
(c15)M1 (c32)M3;
(c32)M3;
生产企业的利润与生产企业在产品研发上的资金投入相关:
(c32)M3 (c33)M3;
(c33)M3;
根据定义2,可得如下基元相关矩阵:
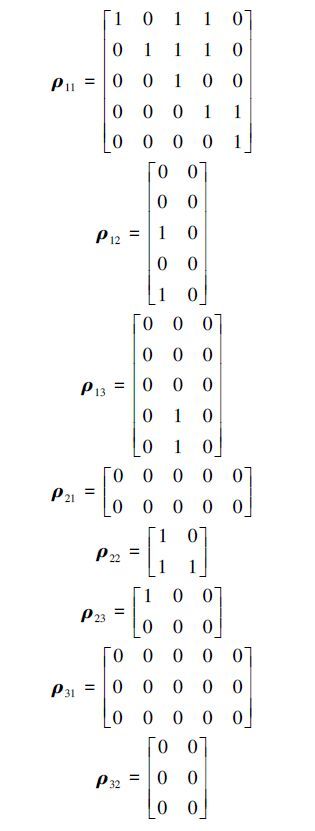



上述所有的“f”均可由已有领域知识或采用数据挖掘方法来获得。例如,利润=(价格-成本)*销售量,故有
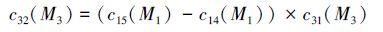
假设生产企业通过改变已有产品的材质和结构进行新产品的开发,则有如下主动变换:

则U0(T1)=(1,1),(1,2)。根据传导推理规则2有:U1(T1)=(1,3),(1,4);则根据传导推理规则1,T1一次传导变换集合为
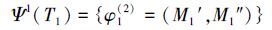
产品材质和结构的变化使得产品的成本和功用性能发生改变,其改变程度即为相应的一次传导变换效应(根据原理1)
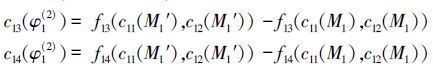
根据传导推理规则4有U2(T1)=(1,5), (2,1),(3,2);则根据传导推理规则3,T1的二次传导变换集合为

产品成本的变化进一步引起产品价格和生产企业利润发生变化;产品功用性能的变化进一步引起消费者购买产品意愿的改变,其改变程度即为相应的二次传导变换效应(根据原理2):

根据传导推理规则6有:U3(T1)=(2,1),(3,2),(3,1),(3,3);则根据传导推理规则5,T1的三次传导变换集合为
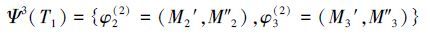
产品价格的变化再次引起消费者购买产品意愿和生产企业利润的变化;消费者购买产品意愿的改变引起销售量的改变;生产企业利润的变化又会引起其在产品研发上的资金投入的改变,其改变程度即为相应的三次传导变换效应(根据原理3):

这里,仅示范性地给出3次传导变换的结果和传导效应的计算方法。据此,由产品的材质和结构的改变,可以确定它所引起的一系列传导变换的结果,为合理地选择主动变换、实现生产企业利润的增长提供依据。
5 结论可拓学的发展为矛盾问题的智能化处理提供了形式化、可操作性好的方法。为了更好地求解复杂系统中的矛盾问题,可拓理论中的传导变换理论有待于在普适性方面进一步发展:
1)作为矛盾问题处理过程中传导推理的重要依据,已有传导变换理论应从基元相关链和相关环的情况推广至任意基元相关网的情况;
2)本文针对复杂基元相关网,提出了基元相关矩阵和基元相关函数的概念,为基元相关性的形式化表述提供了工具;
3)在此基础上,进一步给出了复杂基元相关网下传导变换对象的判定规则及其传导效应的计算模型;
4)以某企业的产品供销活动为例,通过构建产品供销系统的传导机制对所建立理论进行解读,验证了其有效性。
本文给出了复杂系统矛盾问题处理所涉及的若干理论依据,可为未来工作中相应关键技术的研究作好基础性工作。
| [1] | 黄欣荣. 复杂性科学的方法论研究[M]. 重庆:重庆大学出版社, 2006. |
| [2] | 吴志伟, 袁德成. 关于复杂系统研究的发展情况[J]. 控制工程, 2005, 12(增刊1):10-13,95.WU Zhiwei, YUAN Decheng. Study of the development in complex systems[J]. Control engineering of China, 2005, 12(S1):10-13,95. |
| [3] | 闫八一,王龙, 革明鸣. 近二十年复杂系统研究回顾[J]. 系统科学学报, 2007, 15(3):47-50, 54.YAN Bayi, WANG Long, GE Mingming. The review of study on complexity 20 years[J]. Chinese journal of systems science, 2007, 15(3):47-50, 54. |
| [4] | 曹征,张雪平,曹谢东,等.复杂系统研究方法的讨论[J].智能系统学报,2009, 4(1):76-80. CAO Zheng, ZHANG Xueping, CAO Xiedong, et al. A discussion on methodologies for research into complex systems[J].CAAI transactions on intelligent systems, 2009, 4(1):76-80. |
| [5] | 李小川. 基于可拓变换的产品适应性设计方法研究[D]. 杭州:浙江工业大学, 2009.LI Xiaochuan. Research on adaptability design method of product based on extensible transforming[D]. Hangzhou:Zhejiang University of Technology, 2009. |
| [6] | 周建强,赵燕伟,洪欢欢,等. 基于需求驱动的性能冲突可拓传导变换协调方法[J]. 计算机集成制造系统, 2013, 19(6):1205-1215.ZHOU Jianqiang, ZHAO Yanwei, HONG Huanhuan, et al. Coordination method of extension conductive transformation for performance conflict based-on requirement driven[J]. Computer integrated manufacturing systems, 2013, 19(6):1205-1215. |
| [7] | 何斌, 杨春燕, 蔡文. 关键策略的传导效应[J]. 系统工程理论与实践, 2000, 20(5):84-88.HE Bin, YANG Chunyan, CAI Wen. Conduction effect of key strategy[J]. Systems engineering-theory & practice, 2000, 20(5):84-88. |
| [8] | 蔡文, 杨春燕. 基于传导变换的传导知识研究[J]. 数学的实践与认识, 2008, 38(17):85-88.CAI Wen, YANG Chunyan. Conductive knowledge based on conductive transformation[J]. Mathematics in practice and theory, 2008, 38(17):85-88. |
| [9] | 李珊珊, 刘巍, 高红. 基于可拓基元理论的复杂社会网络分析模型[J]. 科技导报, 2014, 32(36):21-25.LI Shanshan, LIU Wei, GAO Hong. A complex social network analysis model based on extenics basic-element theory[J]. Science & technology review, 2014, 32(36):21-25. |
| [10] | 薛名辉, 邹广天. 基于传导变换的建筑立面形式构成[J]. 城市建筑, 2011, 13(9):105-106.XUE Minghui, ZOU Guangtian. Form constitute of architectural facade based on conduction transformation[J]. Urbanism and architecture, 2011, 13(9):105-106. |
| [11] | 杨春燕, 蔡文. 可拓学与矛盾问题智能化处理[J]. 科技导报, 2014, 32(36):15-20.YANG Chunyan, CAI Wen. Extenics and intelligent processing of contradictory problems[J]. Science & technology Review, 2014, 32(36):15-20. |
| [12] | 杨春燕, 蔡文. 可拓学[M]. 北京:科学出版社, 2014:66-73.YANG Chunyan, CAI Wen. Extenics[M]. Beijing:Science Press, 2014:66-73. |
| [13] | 蔡文, 杨春燕, 何斌. 可拓逻辑初步[M]. 北京:科学出版社, 2004:55-56. |
| [14] | 杨春燕,蔡文,可拓学:理论、方法与应用[M].北京:科学出版社,2013.YANG Chunyan, CAI Wen. Extenics:theory, method and application[M]. Beijing:Science Press, 2013. |
| [15] | 李立希, 杨春燕, 李铧汶. 可拓策略生成系统[M]. 北京:科学出版社, 2006:46-62. |



