数据挖掘是一种从大量数据中发现感兴趣信息的技术,聚类算法在数据挖掘应用中日益广泛。其中,基于密度的聚类算法可以发现任意形状的簇且能够较好地处理噪声数据,越来越受到广泛的关注。DBSCAN算法能够发现任意形状的簇,并有效识别离群点,但聚类之前需要人工选择Eps和minPts 2个参数。当数据量增大时,要求较大的内存支持,I/O消耗也很大;当空间聚类的密度不均匀,聚类间距离相差很大时,聚类质量较差[1, 2, 3]。 针对DBSCAN算法在大型数据库与多密度数据集聚类精度低,计算复杂度高,全局参数人工选取等问题,已有很多学者进行了相关研究:S. Mimaroglu等[4]提出对位向量使用裁剪技术,H. Jiang等[5]提出一种基于划分的DBSCAN算法,B. Borah等[6]提出一种改进的基于抽样的DBSCAN算法,D. Kellner[7]提出基于格点的DBSCAN算法,旨在解决DBSCAN算法在内存占用,处理高维数据和密度分布不均数据聚类效果不好等问题;H. F. Zhou、S. H. Yue、Y.Ma、S.JAHIRABAPKAR和Z. Y. Xiong等[8, 9, 10, 11, 12]基于数据的数学统计特性,确定全局参数;B. Liu[13]提出一种基于密度的快速聚类方法,按照特定维的坐标排序,选择有序的未被标记的在核心对象邻域以外的点作为种子扩展簇。综上所述,基于密度聚类算法的改进点主要集中在全局参数的选择以及提高密度聚类效率等。DBSCAN全局参数选择根据k-dist曲线人工确定,过程繁琐,实用性不高。其他基于统计分析的方法,部分以特定数据分布确定全局参数,而数据分布存在不确定性,以特定分布规定不能准确反映数据的分布特性,使计算出的全局参数不准确;提高密度聚类效率主要集中在区域查询中的代表对象的选择,但是选择的代表对象进行区域查询时存在丢失对象现象,对丢失对象进行查漏操作,一定程度上增加了区域查询的复杂度。
1 DBSCAN算法及改进算法DBSCAN是一种经典的基于密度聚类算法[8],可以自动确定簇的数量,并能够发现任意形状的簇。 Eps近邻表示一个给定对象的Eps半径内的近邻称为该对象的Eps近邻,表示为NEps(p):
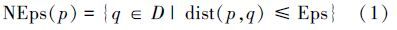
直接密度可达是指对于给定的MinPts和Eps,从对象q可以直接密度可达p,需要满足的条件为

DBSCAN算法的全局参数MinPts和Eps的选取依赖于人工干预,对密度分布均匀的数据根据k-dist曲线升序排列后,人为选择曲线变化幅度开始陡升的点作为Eps参数,并且确定MinPts参数为固定常量4,实施过程繁琐,依赖于人工干预。本文提出一种全局参数自适应选择的方法,根据数据距离空间的统计分布特性,统计出k-dist值的分布情况,曲线拟合出分布曲线,通过计算拟合曲线拐点处对应的值,自适应确定出Eps参数,并根据数据中每个点Eps领域内点数的分布情况,计算出参数MinPts。
DBSCAN以核心对象P来拓展一个簇,通过对包含在P邻域内的点进行区域查询扩展簇。包含在P邻域的对象相互交叉,Q是P的邻域内的一个对象,如果它的邻域被P中其他对象的邻域所覆盖,那么Q的区域查询操作就可以省略,Q不需要作为种子对象用于类的扩展。因此,用于Q的区域查询时间和Q作为核心对象的内存占用都可以被省去。而一个核心对象边界的对象更有利于作为候选对象被选为种子,因为内部对象邻域往往会被外部对象的邻域覆盖。因此,抽样种子实际上是选择的代表对象能够准确描绘出核心对象邻域形状的问题。实际上,对于密度聚类,在核心对象邻域内相当一部分种子对象可以被忽略,选择核心对象边界的部分代表对象进行类的扩展,从而达到减少区域查询频度的目的。
为了自适应确定合适的全局参数MinPts和Eps,减少内存占用量和I/O消耗,提高DBSCAN的计算效率,基于这些分析,本文提出一种改进的自适应快速算法(adaptive and fast density-based spatial clustering of applications with noise,AF-DBSCAN),旨在以自适应方式确定合理的全局参数MinPts和Eps,以及区域查询时选择部分具有代表性的对象作为种子对象进行类扩展。改进算法描述如下:1)自适应确定全局参数Eps和MinPts;2)将所有点分类,分别标记为核心点、边界点和噪声点;3)删除标记处的噪声点;4)连接距离在Eps距离内的所有核心点,并归入到同一簇中;5)各个簇中的核心点对应种子代表对象的选择;6)遍历数据集,根据选择的代表对象进行区域查询,将边界点分入与之对应核心点的簇中。如果数据集中所有点都被处理,算法结束。
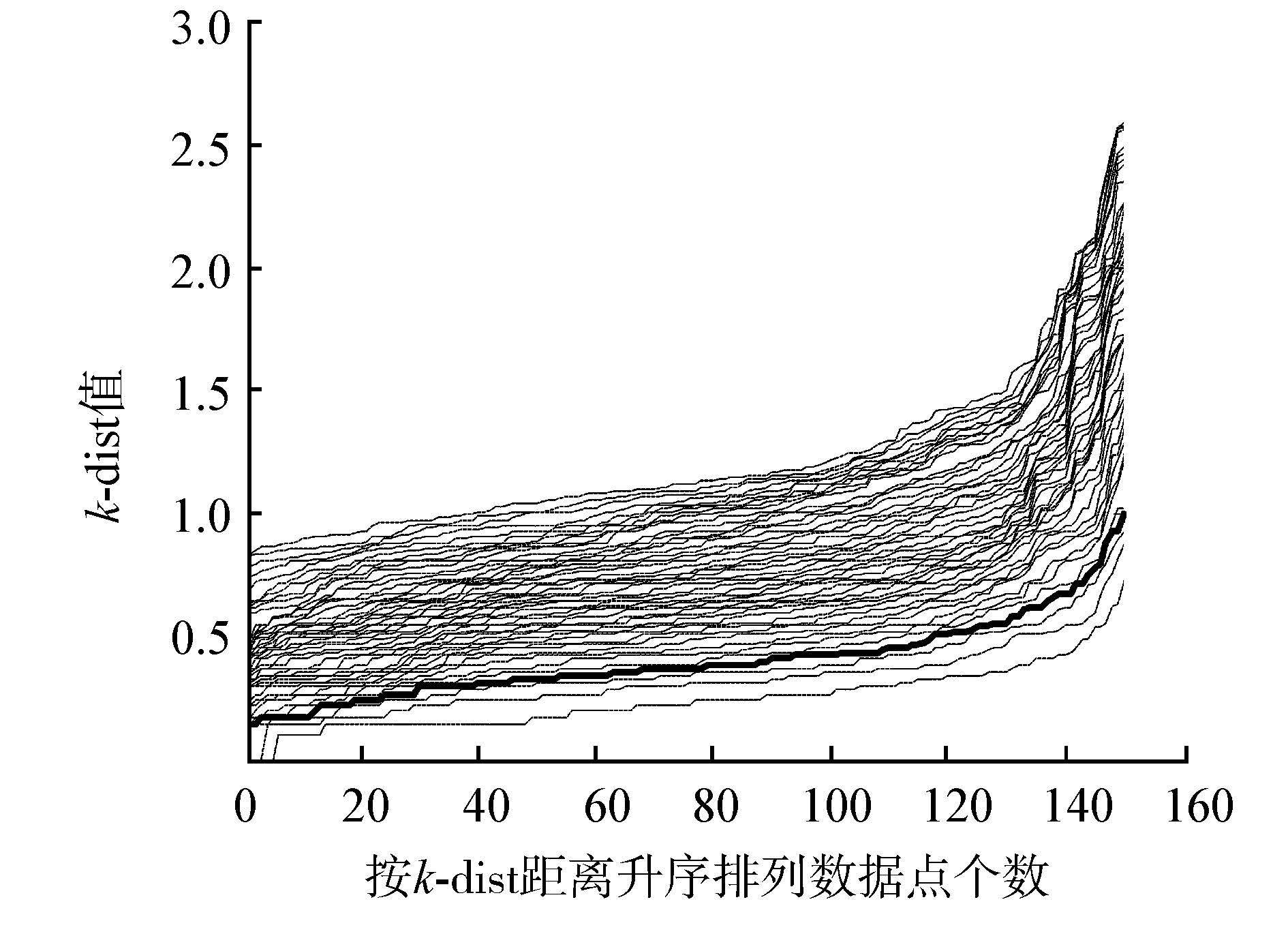
2 AF-DBSCAN聚类算法 2.1 参数Eps与参数MinPts的确定由于密度衡量指标单一,本文算法数据集主要针对簇密度差异不明显的数据。根据输入数据集D计算出距离分布矩阵 DISTn×n,如式(3)所示:
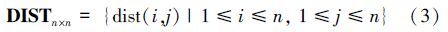
|
| 图 1 KNN分布 Fig. 1 KNN distribution |
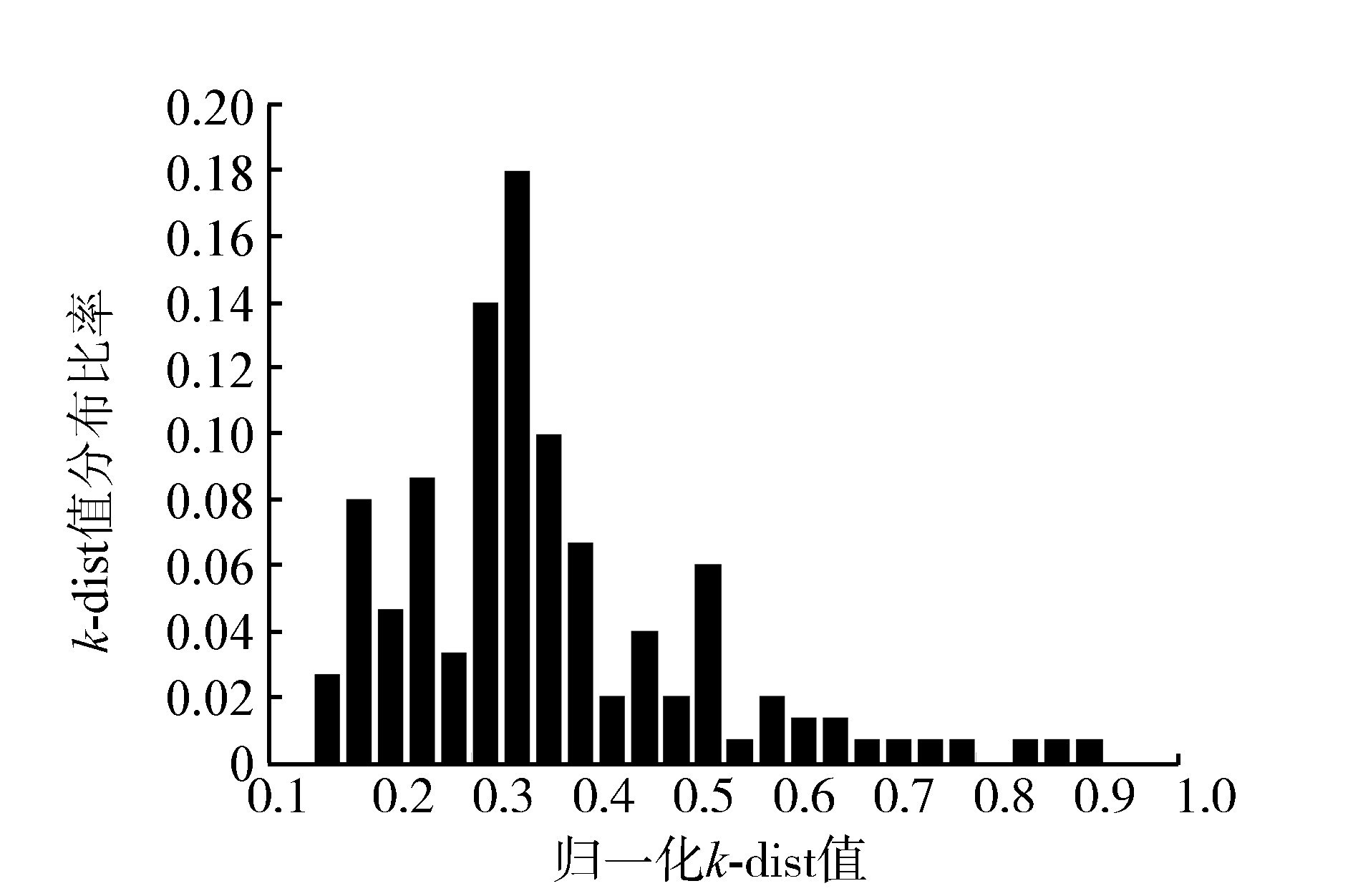
图 1中,k=1,2,…,45,根据k-dist分布曲线可以看出,k=4的dist4曲线可以反映出其他distk曲线的形状。本文选择k=4的distk(k-最近邻距离)的数据进行统计分析,dist4的概率分布图 2所示。
|
| 图 2 distk(k=4)概率分布 Fig. 2 Probability distribution of distk(k=4) |
从图 1可以看出,任何一条曲线都是在平缓变化后急剧上升,distk中大部分值落在一个比较密集的区域内,因此可以判断distk中大部分值应落在一个比较密集的区域内(曲线平缓段)。如果可以通过数学方法找出distk中平缓变化到急剧上升处的点,或者distk概率分布最为密集的区域,则可确定扫描半径参数Eps,所以本文选择图 1中distk拐点处的值为Eps。由图 2可以得到distk的概率分布情况,假如能够通过数学方法找到分布曲线的峰值,也可以用峰值点所对应的k-最近邻距离值(横坐标刻度)作为Eps。
对于概率分布数据,通过分析数据集的统计特性,建立统计模型对数据集进行曲线拟合[14]。本文通过实验对概率分布使用傅里叶、高斯和多项式3种典型曲线拟合方法,如图 3所示。

|
| 图 3 归一化KNN分布拟合曲线 Fig. 3 Fitting curves of normalized KNN distribution |
其中,高斯曲线拟合方法的效果最佳,但是由于概率分布的拟合精度过低,不可用于全局参数Eps的估计。拟合结果为SSE:312.7,R-square:0.675 5,调整R-square:0.651 4,RMSE:3.403,参数SSE和RMSE越接近0拟合越准确;R-square和调整后的R-square越接近于1越准确;高斯拟合曲线如式(4)所示:

根据KNN升序排列曲线确定Eps,对dist4曲线进行拟合。对于升序排列得到KNN分布数据,采用3种拟合方法进行曲线拟合。实验发现高斯拟合精度高,但拟合阶数高,计算复杂度高;傅里叶拟合精度不高;而多项式拟合不仅拟合阶数低,而且拟合精度高,计算复杂度低,拟合结果为SSE:0.046 36,R-square:0.988 3,调整 R-square:0.988,RMSE:0.017 88,如图 4所示。多项式曲线拟合如式(5)所示。
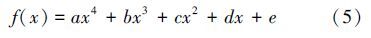

|
| 图 4 多项式拟合曲线 Fig. 4 Polynomial fitting curves |
根据多项式拟合曲线,求解曲线的拐点,对 y求二次导可得f(x)″=12ax2+6bx+2c,求解二次导方程得x的解为x0=${{ - 6b \pm \sqrt {36{b^2} - 96ac} } \over {24a}}$ 。由于较小的值为靠近边界的点,取x解中较大的值,舍去较小的值,将其带入式(5),可以得到Eps=f(x0)。Eps确定后,需要确定MinPts的值。根据每个点邻域数据点的统计分布特性,依次计算出每个点的Eps邻域的对象数量;计算数据对象的数学期望,即MinPts,如式(6)所示:
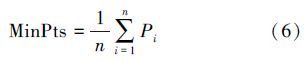
本文将密度聚类算法与基于统计模型相结合,基于数理统计理论,假定数据集由统计过程产生,并通过找出最佳拟合模型来描述数据集,自适应计算出最优全局参数Eps和Minpts。
2.2 种子代表对象的选择本文提出一种改进的基于DBSCAN的快速聚类算法,在通过选用核心对象附近区域包含的所有对象的代表对象作为种子对象扩展类,减少了区域查询的次数,减低了聚类时间和I/O开销。
对于一个给出Eps和MinPts的核心对象P,为了便于阐述,仅考虑二维对象,算法可用于其他大于二维的高维对象。代表对象选择过多则难以发挥算法效率,选择过少则容易造成对象丢失,影响算法聚类质量。FDBSCAN[15]算法在区域查询后,在第1轮核心点区域查询时无丢失对象现象,而在以种子对象进行类扩展时,产生丢失对象,因此需要选择足够多的代表对象;而I-DBSCAN[6]在二维数据中采用至多8个代表对象,不存在对象丢失的情况。本文结合FDBSCAN与I-DBSCAN,第1轮区域查询时采用4个代表对象进行类扩展,继续扩展类时,选择8个代表对象进行类扩展。本算法在提高查询效率的基础上,解决了类扩展时丢失对象的问题。
本文提出的代表对象选择方式如下:以核心对象p为中心,Eps为半径画圆,以对象p为原点画坐标系交圆周于A、C、E和G 4点,再画2条分别与x轴成45°和135°角的直径交圆周于B、D、F和H 4点。第1轮选择代表对象时,以核心点边界的A、C、E和G点为参照,在p的Eps区域中分别选择离A、C、E和G点最近的点作为代表对象。当对于不同参照点存在离其距离最近的点为同一点时,此点只能被选择1次,且属于第1个参考点的代表对象。如果对象是n维数据,则至多可以选择2n个代表对象。
在继续扩展类选择代表对象时,以核心点边界的A、B、C、D、E、F、G和H点为参照点选择代表对象,其原则为p的Eps区域中选择离参考点对象最近的点作为代表对象,即使1个代表对象到2个以上的参考点都是最近的,它也只被选1次,且归入第1个参考点的代表对象。因此,在二维空间范围内,对任一对象的被选代表对象数最多为8个。一般情况下,对n维空间,由于有3n-1个参考点和2n个象限,因此被选种子数最多为3n-1个,按照以上方式实现区域查询,有效提高聚类效率以及解决对象丢失的问题。
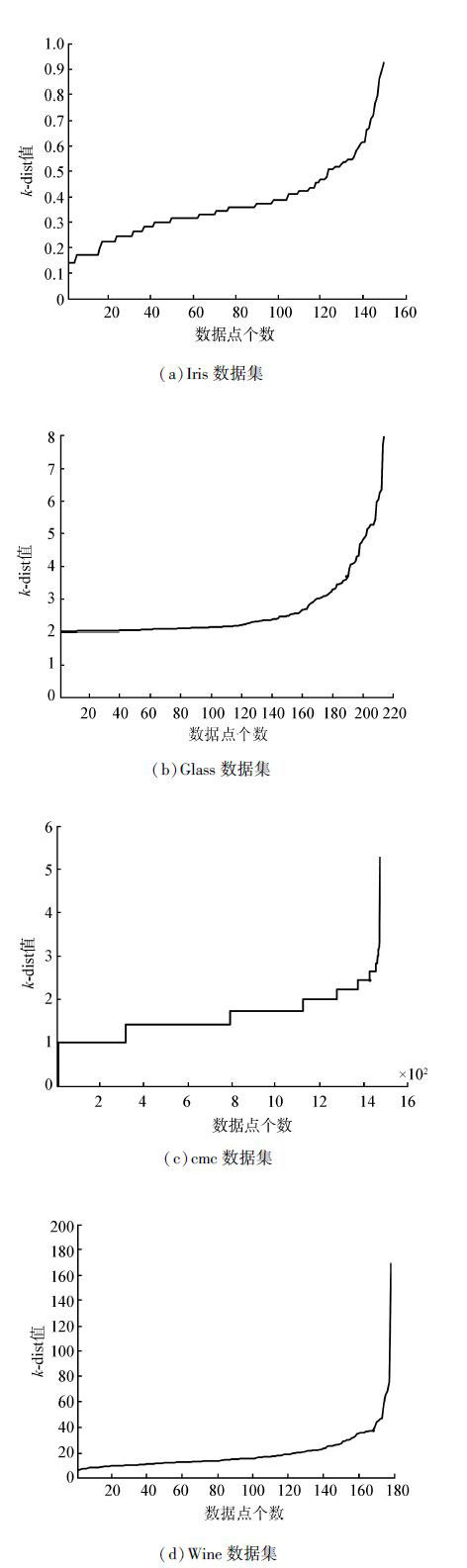
3 实验与分析本文算法采用了Java语言,在Windows XP系统和eclipse环境下运行,PC机硬件配置:Pentium(R) CPU,3 GB内存,300 GB硬盘。为了验证本文改进算法的有效性,根据数据集的维度、数据量和密度分布3种标准进行数据库的选择,选取UCI数据库中的4种典型数据集Iris、Wine、Glass和cmc。根据聚类准确度和时间特性分析2项指标对DBSCAN、I-DBSCAN[8]和AF-DBSCAN算法性能进行比较分析,其中聚类准确度采用F-Measure[13]。DBSCAN中根据k-dist曲线,选取dist4曲线图进行参数Eps值的确定,如图 5所示。
|
| 图 5 dist4曲线 Fig. 5 Curve of dist4 |
根据图 5中平缓变化后急剧上升处对应的k-dist值作为全局参数Eps的值,且Minpts值设为4。得到4种数据集Iris、Wine、Glass和cmc的(Minpts,Eps)分别为(4,0.436)、(4,27.330)、(4,3.700)和(4,1.732)。
本文提出的AF-DBSCAN算法的(Minpts,Eps)分别为(7,0.389)、(6,29.870)、(4,2.695)和(5,1.646)。4种数据集聚类结果如表 1所示。由表 1可以看出,本文提出的AF-DBSCAN算法自适应计算出的全局参数减少了人为根据k-dist曲线确定全局参数Eps的误差及工作量,以及设定MinPts为固定值4,而使聚类结果达不到全局最优的效果。通过比较分析4种数据集的聚类结果,AF-DBSCAN的F-Measure值均优于其他2种典型算法,尤其在Iris和Glass数据集上,聚类精度比DBSCAN算法分别高12.55%和13.18%。而I-DBSCAN算法规定数据符合泊松分布,对于不同数据集F-Measure值不稳定,不能适应不同统计特性的数据集。由于密度衡量指标单一,AF-DBSCAN算法适用于簇密度差异不明显的数据集。经过区域查询改进后的AF-DBSCAN算法,运行速度明显比DBSCAN和I-DBSCAN算法快,有效减少了密度聚类的时间。
| 数据集 | 算法 | MinPts | Eps | 时间/s | 精度 |
| Iris | DBSCAN | 4 | 0.436 | 0.342 | 0.740 7 |
| I-DBSCAN | 6 | 0.405 | 0.335 | 0.8803 | |
| AF-DBSCAN | 7 | 0.389 | 0.157 | 0.866 2 | |
| Wine | DBSACN | 4 | 27.330 | 0.481 | 0.599 4 |
| I-DBSCAN | 6 | 22.890 | 0.467 | 0.566 7 | |
| AF-DBSCAN | 6 | 29.870 | 0.172 | 0.609 1 | |
| Glass | DBSCAN | 4 | 3.700 | 0.516 | 0.656 1 |
| I-DBSCAN | 4 | 2.980 | 0.525 | 0.652 2 | |
| AF-DBSCAN | 4 | 2.695 | 0.188 | 0.787 9 | |
| cmc | DBSCAN | 4 | 1.732 | 3.239 | 0.449 1 |
| I-DBSCAN | 6 | 1.691 | 3.145 | 0.449 1 | |
| AF-DBSCAN | 5 | 1.646 | 1.266 | 0.449 1 |
本文针对DBSCAN算法的参数选取困难,计算效率低以及区域查询中代表对象选择后类扩展易丢失对象点等问题,提出一种改进的自适应快速AF-DBSCAN聚类算法,通过分析数据的KNN的数学统计规律,辅助用户自适应确定全局参数Eps与MinPts。通过改进的区域查询方法,有效提高类扩展的效率,AF-DBSCAN算法解决了DBSCAN算法人工干预,给定全局参数导致聚类质量恶化以及大数据集计算效率低的问题。
| [1] | 吉根林, 姚瑶. 一种分布式隐私保护的密度聚类算法[J]. 智能系统学报, 2009, 4(2):137-141. JI Genlin, YAO Yao. Density-based privacy preserving distributed clustering algorithm[J]. CAAI transactions on intelligent systems, 2009, 4(2):137-141. |
| [2] | SMITI A, ELOUEDI Z. DBSCAN-GM:An improved clustering method based on Gaussian means and DBSCAN techniques[C]//2012 IEEE 16th International Conference on Intelligent Engineering Systems (INES). Lisbon, 2012:573-578. |
| [3] | ZHANG Jiashu, KEREKES J. An adaptive density-based model for extracting surface returns from photon-counting laser altimeter data[J]. Geoscience and remote sensing letters, 2015, 12(4):726-730. |
| [4] | MIMAROGLU S, AKSEHIRLI E. Improving DBSCAN's execution time by using a pruning technique on bit vectors[J]. Pattern Recognition Letters, 2011, 32(13):1572-1580. |
| [5] | JIANG Hua, LI Jing, YI Shenghe, et al. A new hybrid method based on partitioning-based DBSCAN and ant clustering[J]. Expert systems with applications, 2011, 38(8):9373-9381. |
| [6] | BORAH B, BHATTACHARYYA D K. An improved sampling-based DBSCAN for large spatial databases[C]//Proceedings of International Conference on Intelligent Sensing and Information Processing(ICISIP). Chennai, India, 2004:92-96. |
| [7] | KELLNER D, KLAPPSTEIN J, DIETMAYER K. Grid-based DBSCAN for clustering extended objects in radar data[C]//2012 IEEE Intelligent Vehicles Symposium. Alcal de Henares, Madrid, Spain, 2012:365-370. |
| [8] | ZHOU Hongfang, Wang Peng, LI Hongyan. Research on adaptive parameters determination in DBSCAN algorithm[J]. Journal of information & computational science, 2012, 9(7):1967-1973. |
| [9] | YUE Shihong, LI Ping, GUO Jidong, et al. A statistical information-based clustering approach in distance space[J]. Journal of Zhejiang university science, 2005, 6A(1):71-78. |
| [10] | MA Yu, GAO Yuling, SONG Shaoyun. The algorithm of DBSCAN based on probability distribution[C]//5th International Symposium on IT in Medicine and Education. Xining, China, 2014:2785-2792. |
| [11] | JAHIRABADKAR S, KULKARNI P. Algorithm to determine ε-distance parameter in density based clustering[J]. Expert systems with applications, 2014, 41(6):2939-2946. |
| [12] | XIONG Zhongyang, CHEN Ruotian, ZHANG Yufang, et al. Multi-density DBSCAN algorithm based on density levels partitioning[J]. Journal of information and computational science, 2012, 9(10):2739-2749. |
| [13] | LIU Bing. A fast density-based clustering algorithm for large databases[C]//2006 International Conference on Machine Learning and Cybernetics. Dalian, China, 2006:996-1000. |
| [14] | 夏鲁宁.SA-DBSCAN:一种自适应基于密度聚类算法[J]. 中国科学院研究生院学报, 2009, 26(4):530-538. XIA Luning. SA-DBSCAN:A self-adaptive density-based clustering algorithm[J]. Journal of the graduate school of the Chinese academy of sciences, 2009, 26(4):530-538. |
| [15] | 周水庚, 周傲英, 曹晶, 等. 一种基于密度的快速聚类算法[J]. 计算机研究与发展, 2000, 37(11):1287-1292. ZHOU Shuigeng, ZHOU Aoying, CAO Jing, et al. A fast density-based clustering algorithm[J]. Journal of computer research & development, 2000, 37(11):1287-1292. |



