2. 清华大学自动化系, 北京 100086
2. Department of Automation, Tsinghua University, Beijing 100086, China
机器学习在人工智能领域的研究中具有十分重要的地位。目前,其应用已遍及人工智能的各个分支,如模式识别、计算机视觉、数据挖掘、医学诊断、自然语言处理等领域[1, 2, 3, 4, 5, 6]。概率模型则是模式识别中被研究较多的一类模型,它给予了数据产生的复杂现象和内在机理的描述方式。其中,贝叶斯理论是基于概率表达的机器学习的主要工具,其认为:先验信息反映了试验前对总体参数分布的认识,在观察到样本信息后,对此认识有了改变,其结果反映在后验信息中,后验信息综合了样本信息和参数的先验信息[7]。
产生式模型(generative model)和判别式模型(discriminative model)是2个比较常见的有监督学习的分类模型。产生式模型可以指定数据结构的先验信息,但需要对观测数据建立正确的模型,而不是对类别分布进行建模,如贝叶斯决策理论;判别式模型则是通过最大化类别的概率学习模型,如Logistic Regression (LR)[8, 9]。然而,在实际使用中,贝叶斯决策理论仍然存在着一定的局限性。
贝叶斯决策理论是解决模式分类问题的一种基本统计方法。该理论的出发点是利用概率的不同分类决策与相应的决策代价之间的定量折中;目的则是对未知的数据所属的类别做出判决[10]。由于缺乏对于数据结构的信息,贝叶斯决策理论中类条件概率密度函数通常是很难准确估计的。
目前,估计类条件概率密度函数的方法主要有2种,但两者都是基于一定的假设条件。第一种是假设类条件概率密度函数服从多元高斯分布,简称为高斯判别分类器(Gaussian discriminant classifier,GDC)[11]。然而,多元高斯分布的边缘分布是一元高斯分布,该一元高斯分布并非和实际特征的概率分布相吻合。所以,该假设条件并不能准确地表现出多元变量的依赖结构。更重要的是,多元高斯分布中的协方差矩阵只能反映出各个特征之间的线性关系,难以精确地描述特征之间的非线性关系。第2种则是基于朴素贝叶斯条件独立的特点,假设类条件概率密度函数服从若干个一元高斯分布,简称为高斯朴素分类器(Gaussian naive Bayes classifier,GNBC)[12]。该假设条件虽然可以有效地减少参数估计的个数,但它过于简单,直接忽略了各个特征之间的依赖结构。因此,该方法也不能准确地估计出多个特征的联合分布。
由上述可知,现有的估计方法都存在着一定的不足和局限性。本文考虑了特征之间存在的依赖关系,提出了将贝叶斯决策理论和Copula理论相结合的分类器,简称为Bayesian-Copula判别分类器。该模型将Copula函数和核密度估计相结合构建类条件概率密度函数。Copula函数能够描述变量间的线性或者非线性相关性,该理论表明多元联合分布函数可以通过Copula函数和任意的随机变量的边缘分布函数构建[13, 14, 15]。而核密度估计则是一种非参数估计方法,它不需要假设概率分布的形式,可以直接计算得到概率密度值[16]。最后,将改进的BCDC算法用于生物电信号分类识别的实际问题中进行模型的验证。由于从生物电信号中提取的特征之间存在依赖关系,在分类精度和AUC两个指标上,相比于传统的GDC、GNBC和LR模型,所提出的方法呈现出更好的分类效果。因此,该模型可以被用于处理特征间存在一定的相关性的实际问题,为机器学习问题提供了一种新的方法。
1 Bayesian-Copula 判别分类器 1.1 贝叶斯决策理论贝叶斯决策理论表明对未知的数据x所属的类别做出判决,可以通过计算x属于某一个类别的概率值得到,因此通过贝叶斯公式,该概率值可表示为
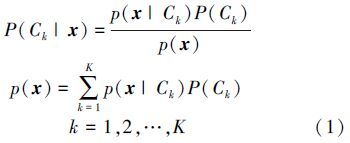
根据最小化误差概率的准则,未知数据x将被归于后验概率P(Ck|x)最大的类别。考虑到p(x)只是一个标量因子,所以式(1)可以简化为
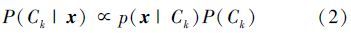
注意到,在式(2)中,后验概率P(Ck|x)主要由先验概率P(Ck)和类条件概率密度函数p(x|Ck)的乘积所决定。先验概率P(Ck)可以经验性地获得,计算在训练数据中属于某一类别的数据个数,再除以训练数据的总个数即可得到。
在下面小节中,我们将通过Copula函数和核密度估计的方法来构建类条件概率密度函数。
1.2 Copula理论近年来,在统计领域里,Copula理论引起了研究者的关注。该理论可以理解为:多维随机变量的联合分布函数可以分解成若干个一维的分布函数和一个Copula函数,而Copula函数则将若干个分布函数连接起来,它可以描述随机变量间的依赖关系。目前,该理论被广泛应用于经济、金融等领域[17, 18]。Sklar定理是Copula理论的核心部分,也是Copula理论在统计学中应用的基础,在建立联合分布函数和它们相应边缘分布函数之间的关联中起着关键的作用。
定理 (Sklar定理 (1959)):令H为n个随机变量X1,X2,…,Xn的联合分布函数,令F1(x1),F2(x2),…,Fn(xn)为随机变量的边缘分布函数,如果所有的边缘分布函数都是连续的,那么存在唯一一个Copula函数C满足:
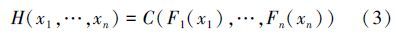
联合密度函数h被定义为

推论 如果C是一个 Copula函数,C的值域为[0,1]n,F1(x1),F2(x2),…,Fn(xn)为随机变量的边缘分布函数,那么C(F1(x1),…,Fn(xn))可以定义一个联合分布函数。
通过Copula理论,式(2)可以被推导出

Copula函数连接的是每个特征的累积分布函数Fi(xi),而累积分布函数的值域是[0,1],因此,当每个特征都是连续的随机变量时,需对数据进行概率积分变换,计算出每个特征的经验累积分布,该方法可以使任意给定的分布转换为均匀分布。
1.3 边缘分布估计式(4)表明,一个联合概率密度函数可以分解为一个Copula密度函数和n个边缘密度函数。非参数估计的方法,如直方图和核密度估计,可以直接利用样本来估计变量的密度函数。考虑到直方图的缺点,核密度估计被用来估计每个特征的概率密度函数。假设有N个样本xi,对于一个新来的样本x,核密度估计的方法可以定义为
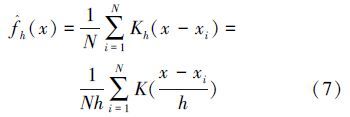
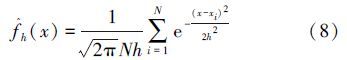
采用极大似然估计的方法对Copula密度函数的参数θ进行估计,可以得到θ的估计值:
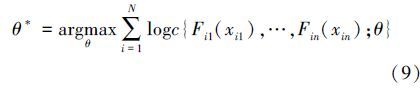
此外,为了校准参数θ,我们充分使用了随机数的性质,从估计的Copula密度函数中生成10 000个随机数,然后用极大似然估计的方法对生成的随机数重新进行参数拟合,估计出最终的参数θ。
1.5 模型选择目前广泛使用的Copula密度函数主要分为两大类:elliptical Copulas和Archimedean Copulas。在本文中,主要使用的是elliptical Copulas中的多元Gaussian Copula函数和多元Student-t Copula函数。
通常,Copula模型的选择会对后续步骤造成一定的影响。因此,贝叶斯信息准则(Bayesian information criterion,BIC)用来对Copula模型进行选择,它是模型拟合程度和模型复杂度之间的权衡,BIC值较小的Copula密度函数会被用于构建类条件概率密度函数。
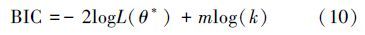
通过检测受试者在白天短时睡眠过程中的困倦状态(drowsiness)和觉醒状态(alertness)这一个实际问题,验证所提出方法的有效性。通常对生物电信号问题进行分析和识别,需要经过信号的数据采集、特征提取和模式分类3个步骤[19, 20, 21, 22]。考虑到从生物电信号中提取的特征参数能反映人的生理状态,而且特征之间可能存在一定的相关性,所以BCDC模型可以用于进行状态检测。
2.1 数据采集共有8名受试者参与了白天短时睡眠的实验,将受试者安排在一个安静舒适的环境内,记录其午后30分钟的睡眠数据。原始睡眠数据的采集按照多导睡眠描记图(PSG,Ploysomnograph)的标准记录方式,包括了4导脑电信号 (C3-A2,C4-A1,O1-A2,O2-A1),并同步采集了2导眼电信号(LOC-A1,ROC-A2),1导肌电信号和1导心电信号。其中脑电、眼电和心电信号的采样频率为100 Hz,肌电信号的采样频率为200 Hz,高频截至频率是30 Hz,时间常数是0.3 s。本文主要分析4导脑电信号(EEG)和2导眼电信号(EOG)。
2.2 特征提取考虑到在20 s的时间内,受试者的状态可能有所变化,因而特征参数可能也会有较大的波动,所以将受试者原始每段20 s的脑电和眼电信号进一步划分为5 s一段和2.5 s的重叠窗,提高特征参数的准确性,并对5 s的数据进行512个点的快速傅立叶变换(FFT),计算每个5 s内脑电信号和眼电信号的特征,对所有5 s的特征参数取平均值,将其作为20 s数据的特征参数,以减少干扰。选取的特征分别对应于 C3/C4导联的θ波(4~8 Hz)和 O1/O2导联的α波(8~13 Hz)的脑电能量占空比和左、右眼电信号的频域能量和(2~10 Hz),即特征向量x={Dθ ,Dα ,SLOC ,SROC}。特征参数计算公式如表 1。
| 信号 | 意义 | 特征参数 |
| EEG | 能量占空比/% | Dθ= max{${{{S_\theta }\left( {{C_3}} \right)} \over {{S_T}\left( {{C_3}} \right)}}$×100%,${{{S_\theta }\left( {{C_4}} \right)} \over {{S_T}\left( {{C_4}} \right)}}$×100%} |
| Dα=max{${{{S_\alpha }\left( {{O_1}} \right)} \over {{S_T}\left( {{O_1}} \right)}}$×100%,${{{S_\alpha }\left( {{O_2}} \right)} \over {{S_T}\left( {{O_2}} \right)}}$×100%} | ||
| EOG | 频域能量和/μV2 | SLOC(LOC),SROC(ROC) |
表 1中θ (4~8Hz),α(8~13 Hz),T(0.5~25 Hz);LOC,ROC(2~10 Hz)。
2.3 模式分类2.3.1 参数优化和模型选择
首先,对数据集做归一化处理,随机选取70%的数据作为训练数据,30%的数据作为测试数据进行分析。然后,针对每一个类别,通过概率积分变换计算训练数据中4个特征的经验累积分布,并用kendall秩相关系数表示两两特征之间的相关性。相关性如下所示:
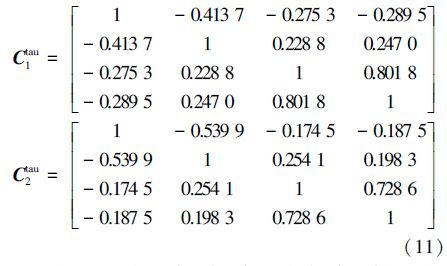
从以上2个矩阵可知,每一个类别的特征之间存在正、负相关性,有些特征间的相关性比较微弱,这主要是由于不同的受试者对2个状态存在一定的差异性。
随后,对Copula密度函数的参数θ进行极大似然估计,并用随机数的性质重新校准参数θ。最后,采用BIC选取最合适的Copula密度函数,并与核密度估计相结合,构建类条件概率密度函数,BIC选取的模型如表 2所示。
| Copula密度函数 | 觉醒状态(A) | 困倦状态(D) |
| Gaussian Copula | -451.63 | -477.25 |
| Student-t Copula | -459.46 | -471.83 |
BIC值较小的Copula函数会被选择,所以针对alertness类别选取的是Student-t Copula函数,而drowsiness类别选取的是Gaussian Copula函数。
2.3.2 模式分类和模型比较
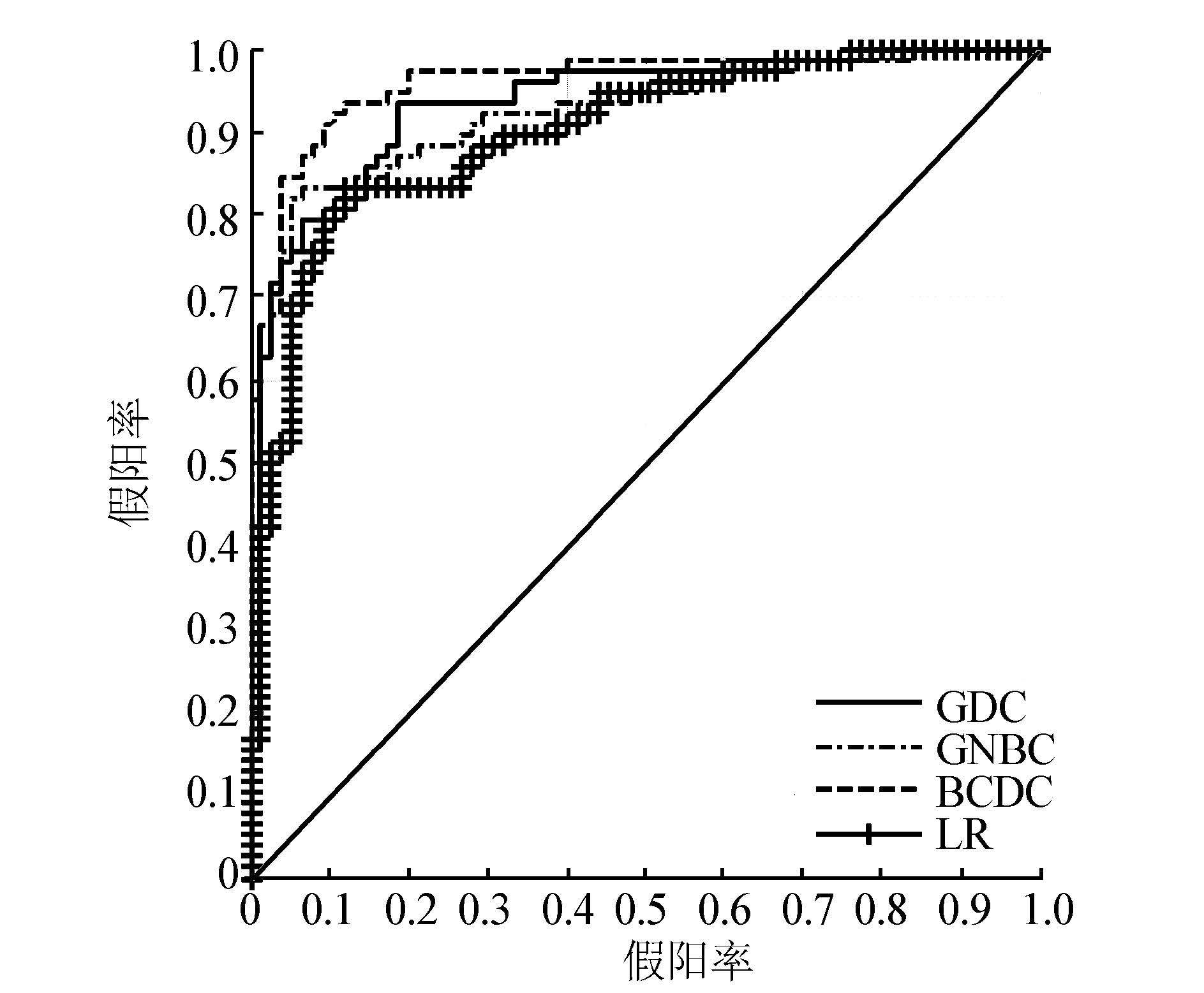
将改进的BCDC算法与GDC、GNBC和LR对测试数据进行分析和比较。ROC曲线被用来表现分类器的性能,它通过将连续变量设定出多个不同的阈值来揭示真阳率(true positive rate,TPR)和假阳率(false positive rate,FPR)的相互关系。其横轴表示真阳率,纵轴表示假阳率,曲线下面积越大,分类器分类的能力越强。图 1呈现出4个分类器在测试数据上的ROC曲线,其中连接点(0,0)和(1,1)的直线表示随机猜测。相比其他3个方法,BCDC算法的曲线处于左上角,所以该方法表现出较好的分类能力。
|
| 图 1 GDC、GNBC、BCDC、LR的ROC曲线 Fig. 1 ROC curves obtained by GDC,GNBC,BCDC,LR,respectively |
为了进一步定量地检验4个分类器识别的准确性,通过分类精度和AUC两个性能指标对分类器进行评价。考虑到训练数据和测试数据是随机选取的,数据中存在的个体差异性可能会影响分类器的性能评估,所以将随机实验循环50次,得到分类器的平均分类精度和平均AUC,如表 3所示。
| 分类器 | 平均精度(标准差) | 平均AUC(标准差) |
| GDC | 0.855 9(0.025 7) | 0.940 8(0.012 9) |
| GNBC | 0.858 8(0.025 8) | 0.925 3(0.016 9) |
| LR | 0.838 2(0.023 9) | 0.912 0(0.017 3) |
| BCDC | 0.902 6(0.017 9) | 0.963 4(0.010 3) |
从表 3可知,本文提出的BCDC算法在两个分类指标上呈现出更好的分类表现。就平均精度而言,BCDC识别的精度高于其他3个分类器大约5%左右,同时标准差也小于其他3个分类器。而对于AUC,尽管GDC相对接近于BCDC,但BCDC的AUC值大于其他3个方法,且标准差也较小,呈现出更强的稳定性。
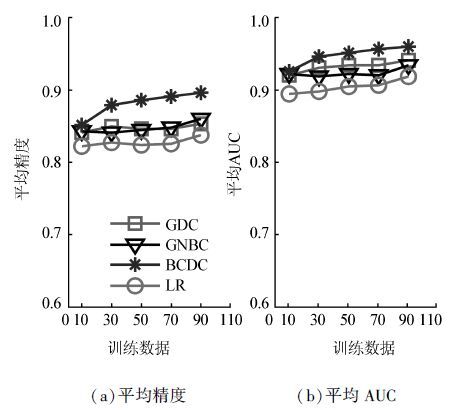
为了了解不同分类器在不同数量的数据集上的分类能力,从数据中分别随机选取10%、30%、50%、70%和90%的数据作为训练数据,用剩余的测试数据评估4个分类方法,结果如图 2所示。
|
| 图 2 GDC、GNBC、BCDC、LR在不同训练数据个数下的平均精度和平均AUC Fig. 2 Average accuracy and average AUC obtained by GDC,GNBC,BCDC,and LR based on the different subsets of the training data |
分析数据可得:当训练数据较少时(10%),4个方法表现出几乎相同的平均精度,BCDC并没有产生显著的识别精度。当训练数据增加(30%),提出的方法的分类表现很快超越了其他3个分类器。当数据量大于30%,BCDC表现出更高的分类表现。总而言之,当30%、50%、70%和90%作为训练数据时,相比较GDC、GNBC、LR,改进的BCDC的分类能力更强。由图 2表明,增加训练数据个数能够提供更多的某种特定类别的信息,从而更加准确地判断类别。
作为一种监督式学习方法,BCDC算法通过参数优化和模型选择提高了类条件概率密度函数估计的准确性。虽然训练时间大约是10 s,但是在不同数据量的条件下,BCDC算法呈现出更好的平均分类精度和平均AUC。
3 结束语本文提出了基于贝叶斯决策理论和Copula理论的分类算法。该算法在实际运用过程中,参数Copula模型和核密度估计相结合提升类条件概率密度函数估计的准确性。相比较其他传统的贝叶斯决策模型,Bayesian-Copula判别分类器能够在实际的生物电信号分类识别问题中得到较好的分类效果。
Copula模型的优势主要是不需要对边缘分布的形式进行假设,在模型中,我们仅仅计算每个特征的经验累积分布,用不同的Copula函数建立特征间的依赖结构。该模型简单、易懂,在对未知数据建立模型时,具有更多的灵活性。对于许多实际问题,概率模型中独立同分布的假设通常是不成立的。所以,通过Copula理论能够提高对联合分布估计的准确性。
要研究方向为控制理论及应用、信号处理、机器人控制等。主持或参与国家973项目、国家863项目、国家自然科学基金项目多项。曾获得教育部自然科学奖、军队科技进步奖、中国电子信息科学技术奖等。发表论文200余篇,其中被SCI检索40余篇,EI检索120余篇。
| [1] | TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of machine learning research, 2001, 1(3):211-244. |
| [2] | XUE Jinghao, HALL P. Why does rebalancing class-unbalanced data improve AUC for linear discriminant analysis?[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(5):1109-1112. |
| [3] | FERNÁNDEZ-DELGADO M, CERNADAS E, BARRO S, et al. Do we need hundreds of classifiers to solve real world classification problems?[J]. Journal of machine learning research, 2014, 15(1):3133-3181. |
| [4] | RODRIGUEZ A, LAIo A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191):1492-1496. |
| [5] | 李宏伟, 刘扬, 卢汉清, 等. 结合半监督核的高斯过程分类[J]. 自动化学报, 2009, 35(7):888-895. LI Hongwei, LIU Yang, LU Hanqing, et al. Gaussian processes classification combined with semi-supervised kernels[J]. Acta automatica sinica, 2009, 35(7):888-895. |
| [6] | BLEI D M, NG A Y, JORDAN M I. Latent dirichlet allocation[J]. Journal of machine learning research, 2001, 3(4-5):993-1022. |
| [7] | BISHOP C M. Pattern Recognition and Machine Learning[M]. New York:Springer, 2006:21-31. |
| [8] | NG A Y, JORDAN M I. On discriminative vs. generative classifiers:a comparison of logistic regression and naïve Bayes[C]//Advances in Neural Information Processing Systems. Vancouver, British Columbia, Canada, 2002, 14:841-848. |
| [9] | 李航. 统计学习方法[M]. 北京:清华大学出版社, 2012:77-91. |
| [10] | JAIN A K, DUIN R P W, MAO Jianchang. Statistical pattern recognition:a review[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(1):4-37. |
| [11] | DUDA R O, HART P E, STORK D G. Pattern Classification[M]. 2nd ed. New York:Wiley, 2001:20-45. |
| [12] | MURPHY K P. Machine Learning:A Probabilistic Perspective[M]. England:MIT, 2012:82-87. |
| [13] | NELSEN R B. An Introduction to Copulas[M]. 2nd ed. Springer:Berlin, 2006. |
| [14] | GENEST C, FAVRE A C. Everything you always wanted to know about Copula modeling but were afraid to ask[J]. Journal of hydrologic engineering, 2007, 12(4):347-368. |
| [15] | EBAN E, ROTHSCHILD G, MIZRAHI A, et al. Dynamic Copula networks for modeling real-valued time series[C]//Proceedings of the 16th International Conference on Artificial Intelligence and Statistics. Scottsdale, AZ, USA, 2013, 4:247-255. |
| [16] | KRISTAN M, LEONARDIS A, SKOC AJ D. Multivariate online kernel density estimation with Gaussian kernels[J]. Pattern recognition, 2011, 44(10-11):2630-2642. |
| [17] | CHERUBINI U, LUCIANO E, VECCHIATO W. Copula Methods in Finance[M]. England:John Wiley & Sons, 2004. |
| [18] | PATTON A J. A review of Copula models for economic time series[J]. Journal of multivariate analysis, 2012, 110:4-18. |
| [19] | AUBASI A. Classification of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders[J]. Computers in biology and medicine, 2013, 43(5):576-586. |
| [20] | TAGLUK M E, SEZGIN N, AKIN M. Estimation of sleep stages by an artificial neural network employing EEG, EMG and EOG[J]. Journal of medical systems, 2010, 34(4):717-725. |
| [21] | CICHOCKI A, MANDIC D, DE LATHAUWER L, et al. Tensor decompositions for signal processing applications:from two-way to multiway component analysis[J]. IEEE signal processing, 2015, 32(2):145-163. |
| [22] | KHUSHABA R N, KODAGODA S, LAL S, et al. Driver drowsiness classification using fuzzy wavelet-packet-based feature-extraction algorithm[J]. IEEE transactions on biomedical engineering, 2011, 58(1):121-131. |



