2. 中国民航大学理学院, 天津 300300
2. College of Science, Civil Aviation University of China, Tianjin 300300, China
现如今无论是基于传递函数的经典控制理论,还是基于状态空间模型的现代控制理论,大部分控制器的设计都是基于模型的。然而基于模型的控制理论不可避免地需要对被控对象进行建模,但是建立被控对象的数学模型并不是一件易事,尤其是对于非线性系统来说,需要耗费巨大的人力物力。无模型控制思想的提出恰恰能解决上述基于模型的控制方法存在的问题。无模型控制就是无需建立被控对象的数学模型而能实现控制的一种方法。其实在工业应用中最广泛的PID控制方法就是最原始的无模型控制思想的应用,然而PID方法最大的缺点就是控制器参数不易调节。无模型控制方法现阶段没有固定的控制器结构与设计方式,广义上来说,所有不基于数学模型设计控制器的方法都可称之为无模型控制。
现在无模型控制方法得到了越来越多国内外专家的重视,有的已经在工业过程中得以应用。文献[1, 2, 3]为基于动态线性化的无模型控制方法,在每一离散时刻对系统进行线性化处理,然后可以利用线性系统理论求解问题。在无模型控制方法中,神经网络因其结构的特殊性,发挥着巨大的作用。如文献[4]中提出以函数近似结构(可采用神经网络)作为其控制器,以同时扰动随机逼近算法估计梯度的无模型控制方法。文献[5]以前馈神经网络作为无模型自适应控制器结构,运用BP算法训练控制器参数,所设计控制器已广泛应用于工业过程控制中。文献[6]介绍了基于数据的自学习优化控制方法,采用函数近似结构来估计系统性能指标函数,然后依据最优性原理来获得最优的控制策略。文献[7]采用双神经元作为控制器结构,主神经元控制器用来控制PH过程,子神经元控制器用来补偿其非线性。本文则采用递归神经网络中的Elman网络作为控制器结构,并且采用粒子群优化算法训练神经网络权值参数,从而得到控制量,无需从被控对象的数学模型出发设计控制器,实现系统的无模型控制。
1 Elman无模型控制系统下面以SISO离散非线性系统作为被控对象,
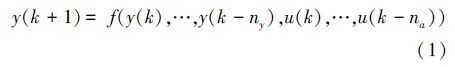

|
| 图 1 Elman无模型控制系统 Fig. 1 Elman model-free control system |
设计控制器的原则是,在每一个离散时刻寻找一组最优的控制器参数(权值参数),使得以下控制性能指标函数达到最小。
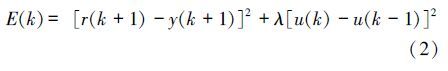
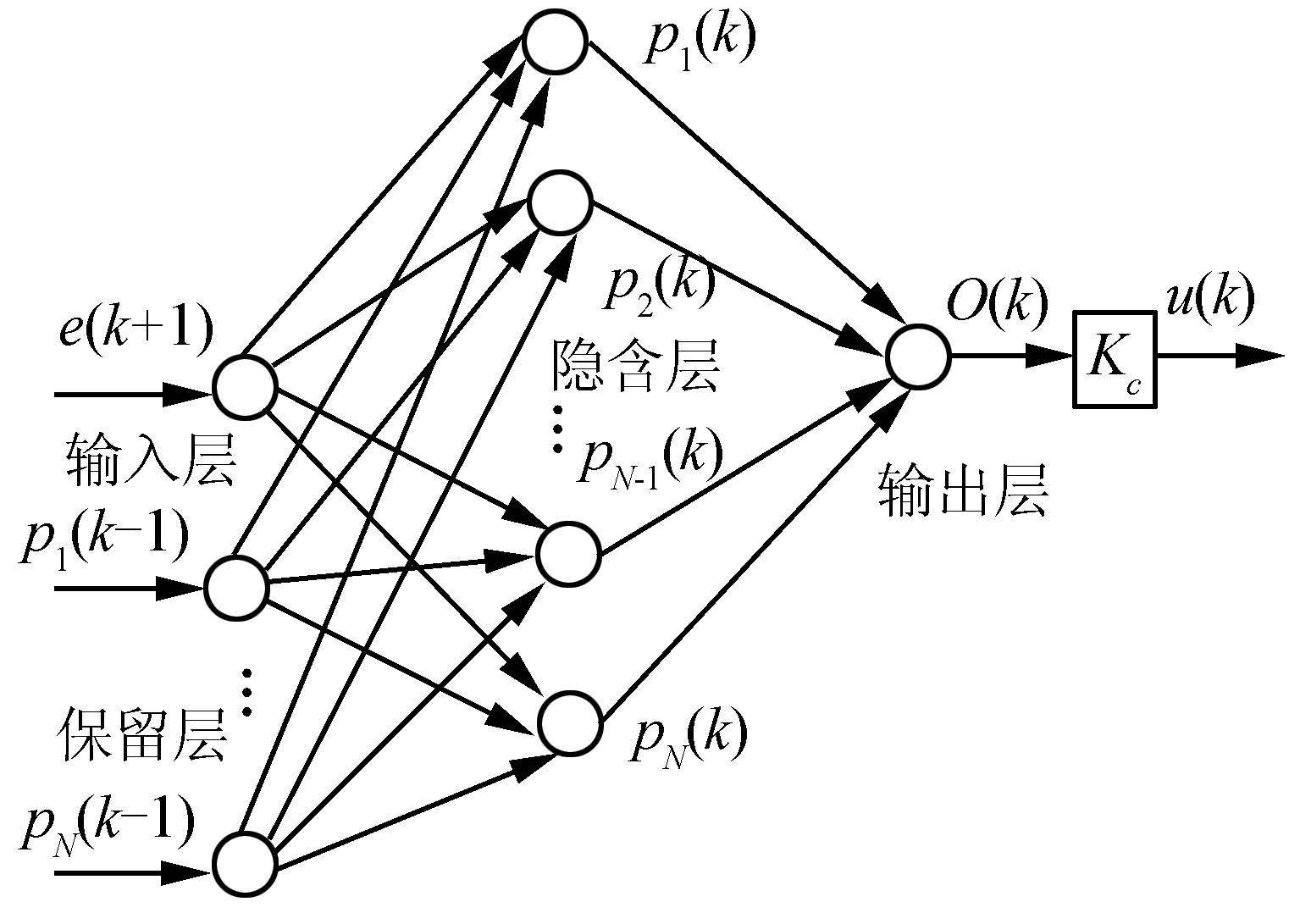
也就是说控制器能在每个离散时刻k产生一个控制量u(k),使得实际输出y(k)跟随设定值r(k)变化。这里采用递归神经网络中的典型结构Elman网络作为控制器的结构,如图 2所示,其中网络的结构固定,不随时间变化,网络的权值参数可以随时间不断进行更新学习。
|
| 图 2 Elman无模型控制器 Fig. 2 Elman model-free controller |
Elman网络是由J.L Elman于1990年针对语音问题提出来的一种多层动态神经网络[8]。由于其结构具有动态递归的特点,对非线性函数有很好的逼近能力,因此被广泛应用于控制系统的设计中[9, 10]。Elman网络分为4层:输入层、隐含层、输出层和保留层。其输入层、隐含层和输出层的连接类似于前馈网络,区别在于增加了保留层,用来存储隐含层神经元上一时刻的输出值。隐含层的输出通过保留层的延迟与存储,重新作为隐含层的输入,这种连接方式使得网络对历史状态的数据具有记忆功能,从而增加了网络处理动态信息的能力。其数学描述如下:

最优控制量u(k)的产生依靠Elman神经网络自身权值参数的不断学习产生,最常见的基于梯度的学习算法(如BP算法)需要求取性能指标函数对权值向量(网络中所有权值参数)的偏导。由于被控对象的数学模型未知,其中y(k+1)对u(k)的偏导数是未知的,所以基于梯度的学习算法需要预先估计其梯度值,而且梯度算法需要分别求解目标函数对各层权值的偏导,无法整体统一更新学习,计算略微复杂。针对这一问题,我们引入了粒子群优化算法(particle swarm optimization)来实现权值寻优。
2 粒子群优化算法PSO算法是由Kenny和Eberhart于1995年提出的一种群智能优化算法[11]。它的思想起源于鸟群觅食行为,通过集体协作使群体达到最优,具有高效的全局搜索能力和鲁棒性。这是一种随机、并行的优化算法,不要求目标函数具有可微、可导、连续等性质,也不需要去求解目标函数的导数,所有待优化参数可以整体统一更新学习,恰恰解决了梯度学习算法所存在的问题。
2.1 算法介绍粒子群优化算法因其算法自身的优越性在许多领域具有广泛的用途,如函数优化、神经网络训练、多目标优化等 [12, 13, 14]。
在粒子群优化算法中,被优化问题的解可以想象成搜索空间中的一个“粒子”,也就是说每个粒子的位置就是一个潜在的解。每个粒子都有一个适应度值,由相应的被优化函数决定,还有一个决定其方向和距离的速度向量。在迭代寻找最优解的过程中,通过适应度函数估计每个粒子的适应度值,从而获得两个极值,一个是整个种群目前找到的最优解,即全局极值;另一个是各个粒子目前找到的最优解,即个体极值[15]。
假设搜索空间为D维,一个由若干粒子组成的群体在搜索空间中飞行,粒子i的位置表示为:xi=(xi1,xi2,…,xiD);粒子i的速度表示为:vi=(vi1,vi2,…,viD);粒子i个体历史最优位置表示为:pi=(pi1,pi2,…,piD);群体内所有粒子经历的最优位置表示为:pg=(pg1,pg2,…,pgD)。
粒子速度和位置的更新方程为

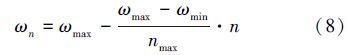
1)在搜索空间中随机生成粒子种群,初始化粒子的位置和速度;
2)在第n次迭代中,根据适应度函数计算每个粒子的适应度,这里以式(2)作为其适应度函数,其中λ=0.5,找出本次迭代中的个体最优位置和群体最优位置;
3)根据位置速度更新式(6)~(8)更新每个粒子的速度和位置;
4)判断是否达到终止条件,即迭代次数是否达到最大迭代次数,如果是则结束迭代;否则n=n+1,转步骤2。
2.3 控制算法流程1)在k时刻,根据给定参考量r(k+1)和输出量y(k),计算当前时刻输出信号与下一时刻参考输入信号的偏差e(k+1)=r(k+1)-y(k);
2)以e(k+1)作为Elman网络输入,基于上一时刻保存的最优权值参数下,判断所得的控制量u(k)是否达到目标要求,如果是则转 4),否则就转3);
3)以e(k+1)作为Elman网络输入,利用PSO优化算法得到最优权值参数向量,从而得到k时刻的控制量u(k);
4)将所得最优控制量u(k)施加到被控对象,得到输出y(k+1);
5)令k=k+1,转1)。
3 仿真研究为了验证基于粒子群算法的Elman无模型控制方法的有效性,本文选取了2个典型离散非线性系统,对它们的控制性能进行了仿真实验,离散非线性系统分别来自文献[16]和[17]。
本文中Elman 网络输入层就一个神经元,为偏差信号 e(k+1),隐含层与保留层神经元取为4,输出层神经元为1,输出控制量u(k);网络所有权值数量(即粒子向量维数)为24(4+4×4+4=24)。初始输入输出:y(3)=0,y(2)=0,y(1)=0,u(2)=0,u(1)=0。
3.1 仿真模型1离散非线性对象如下:
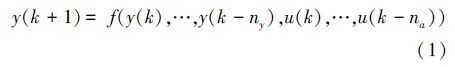
参考控制信号如下:

参考输出信号yr(k)即参考控制输入下所产生的输出值。
控制器参数设置如下:粒子数量取为5,最大迭代次数取为50,微粒初始位置、微粒初始速度随机给定,范围为[-1,1],为了防止搜索时步长过大,速度前面乘以系数0.1,kc=2,c1=c2=2。
仿真结果如图 3~5所示。
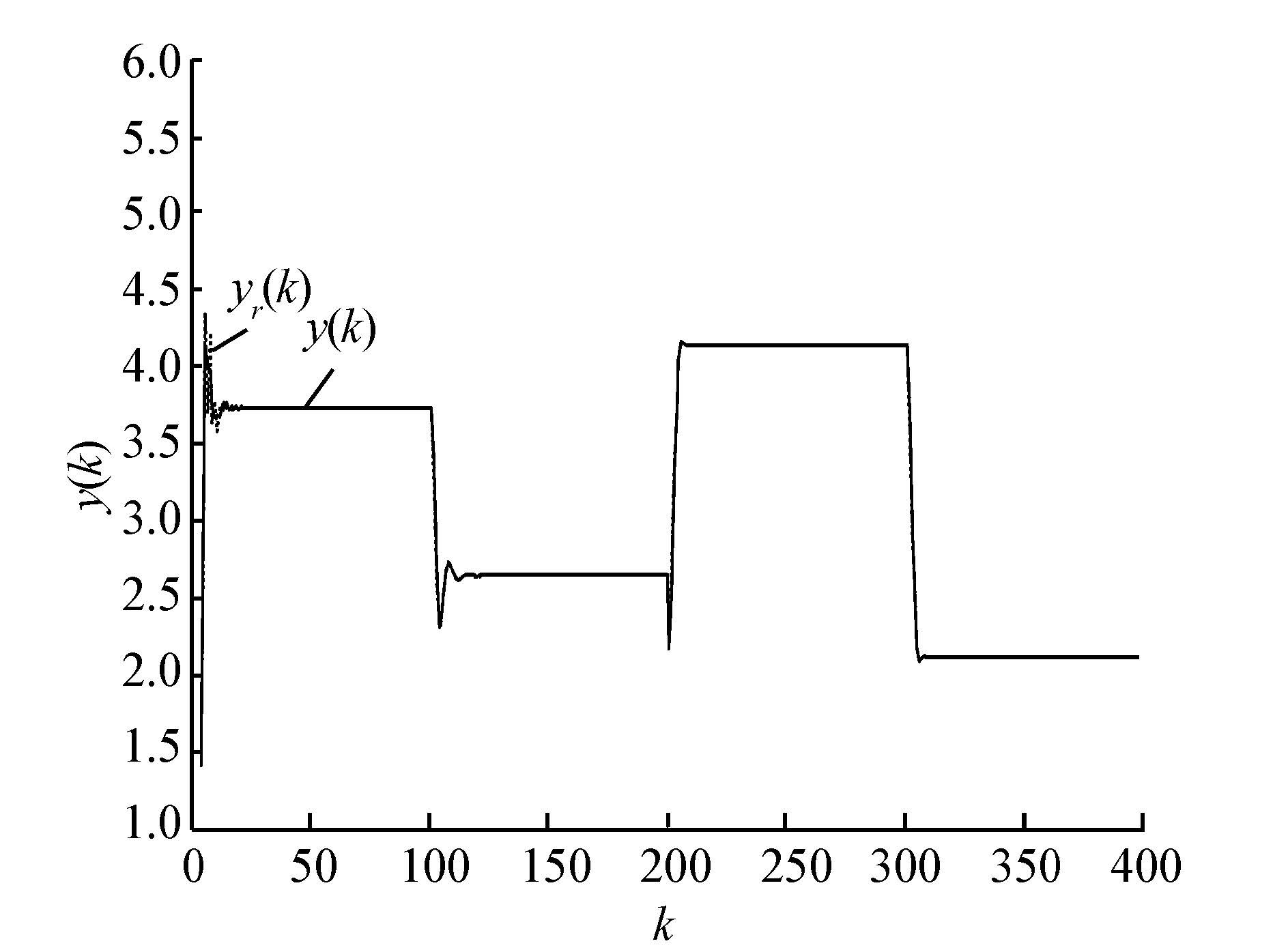
|
| 图 3 模型1中的输出跟踪信号曲线 Fig. 3 Tracking performance curve in model 1 |
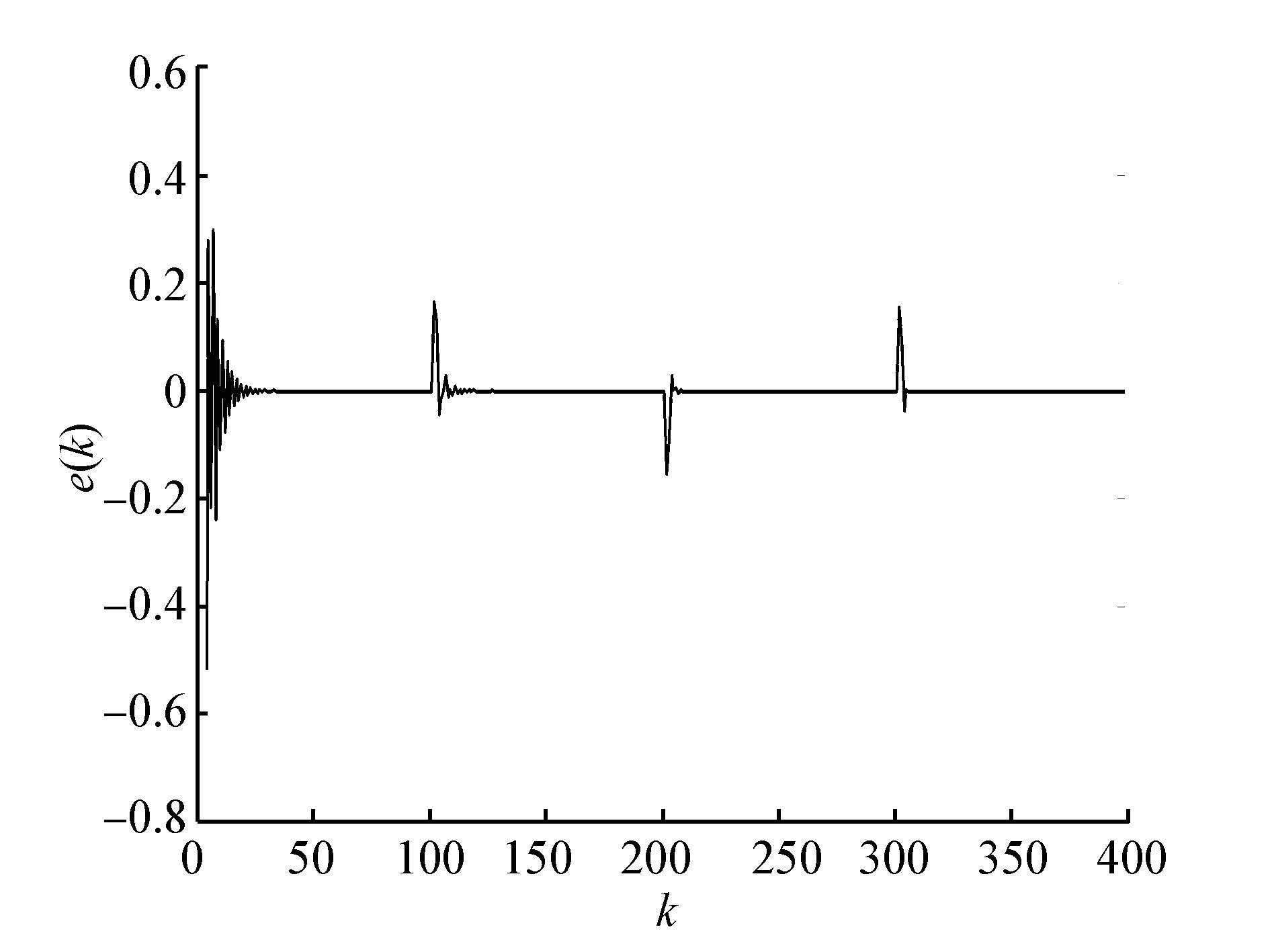
|
| 图 4 模型1中的跟踪误差信号曲线 Fig. 4 Tracking error curve in model 1 |
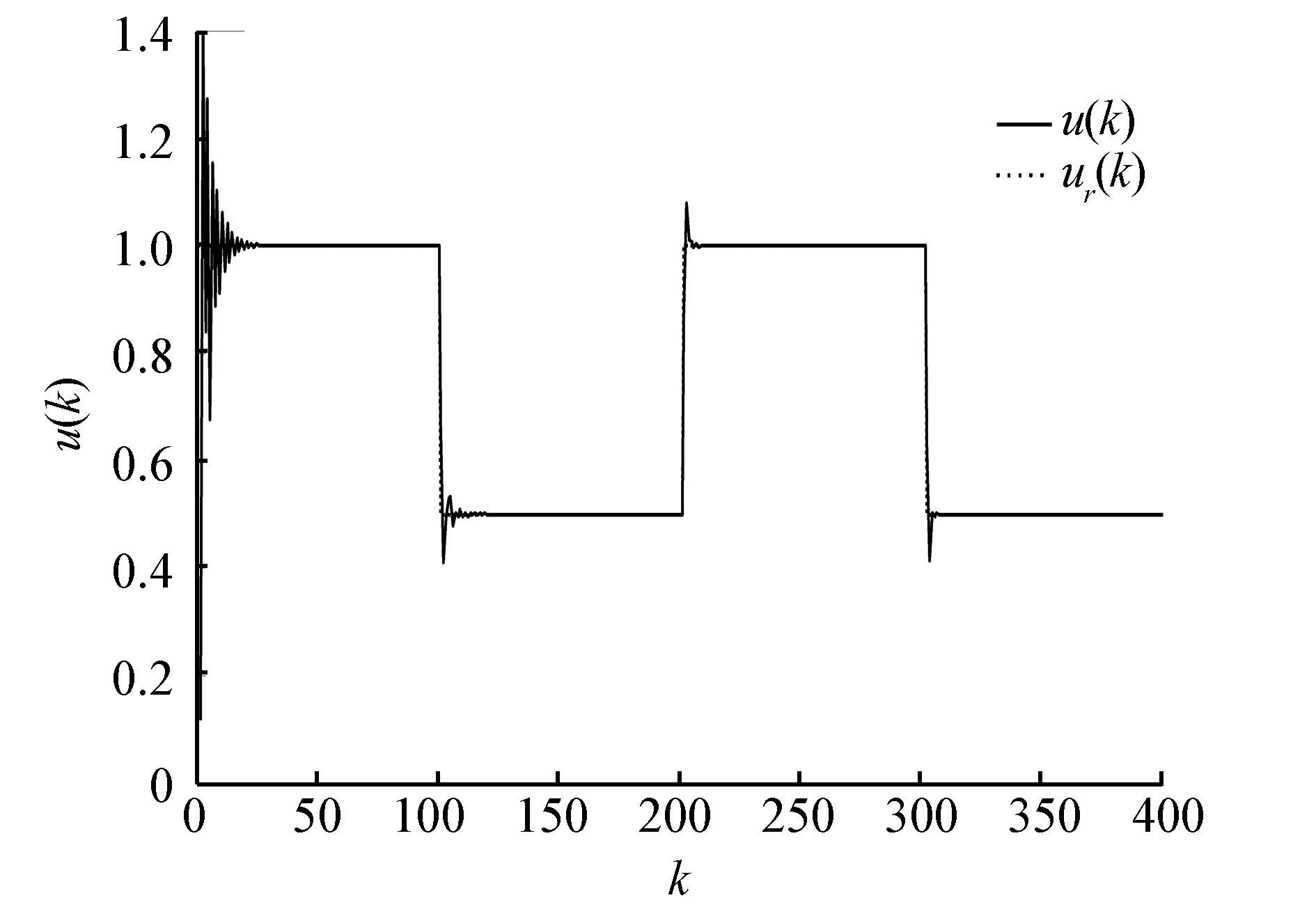
|
| 图 5 模型1中的控制输入信号曲线 Fig. 5 Control input curve in model 1 |
本文为了体现Elman神经网络+PSO控制器算法 优越的控制性能,以模型1为例,与BP神经网络+BP算法的传统组合模式进行了比较,网络输入神经元个数为5,隐含层神经元个数为4,网络权值个数24(5×4+4=24),其他参数调节至最优。其仿真结果如图 6、7所示。

|
| 图 6 BP神经网络+BP算法无模型控制方法的输出跟踪信号曲线 Fig. 6 Tracking performance curve of MFC method with BPNN +BP algorithm |
|
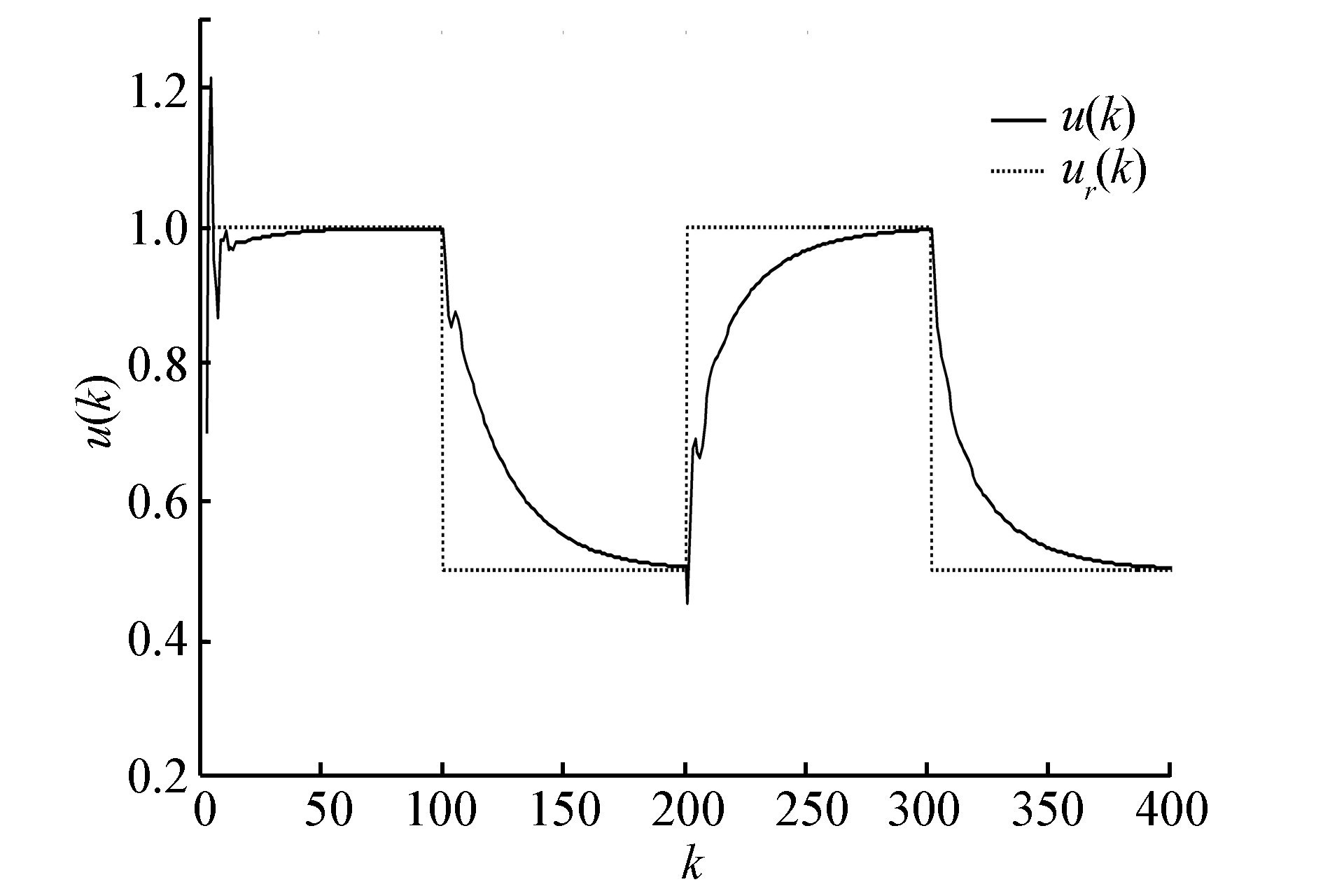
| 图 7 BP神经网络+BP算法无模型控制方法的控制输入信号曲线 Fig. 7 Control input curve of MFC method with BPNN+BP algorithm |
离散非线性对象如下:
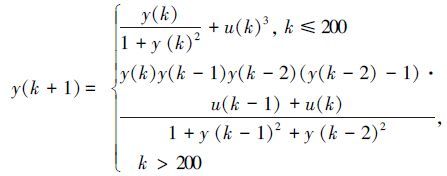
参考控制信号如下:
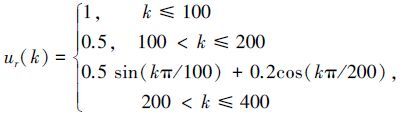
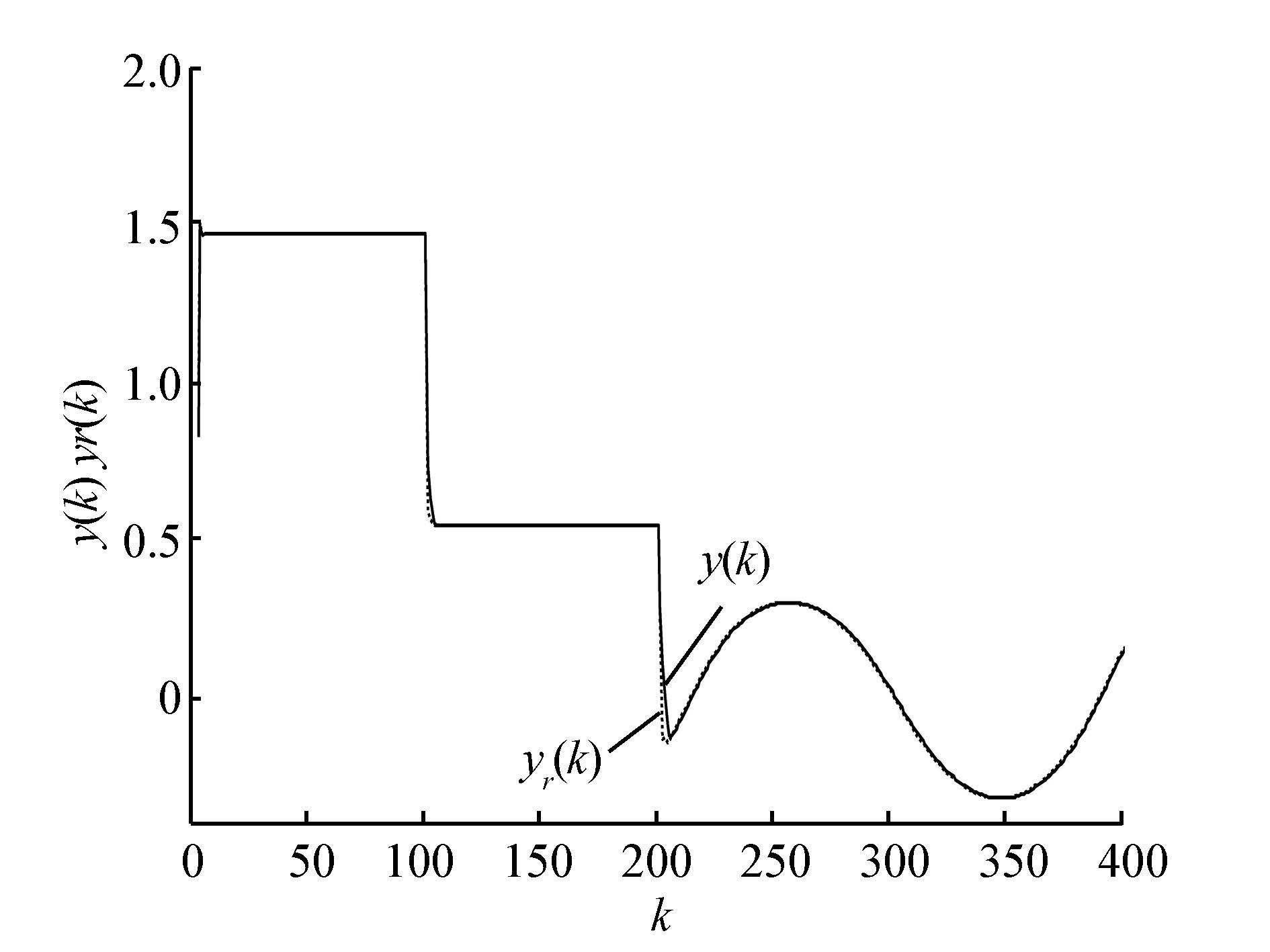
参考输出信号采用在参考控制输入下所产生的输出值。控制器参数设置同模型1,仿真结果如图 8~10所示。
|
| 图 8 模型2中的输出跟踪信号曲线 Fig. 8 Tracking performance curve in model 2 |
|
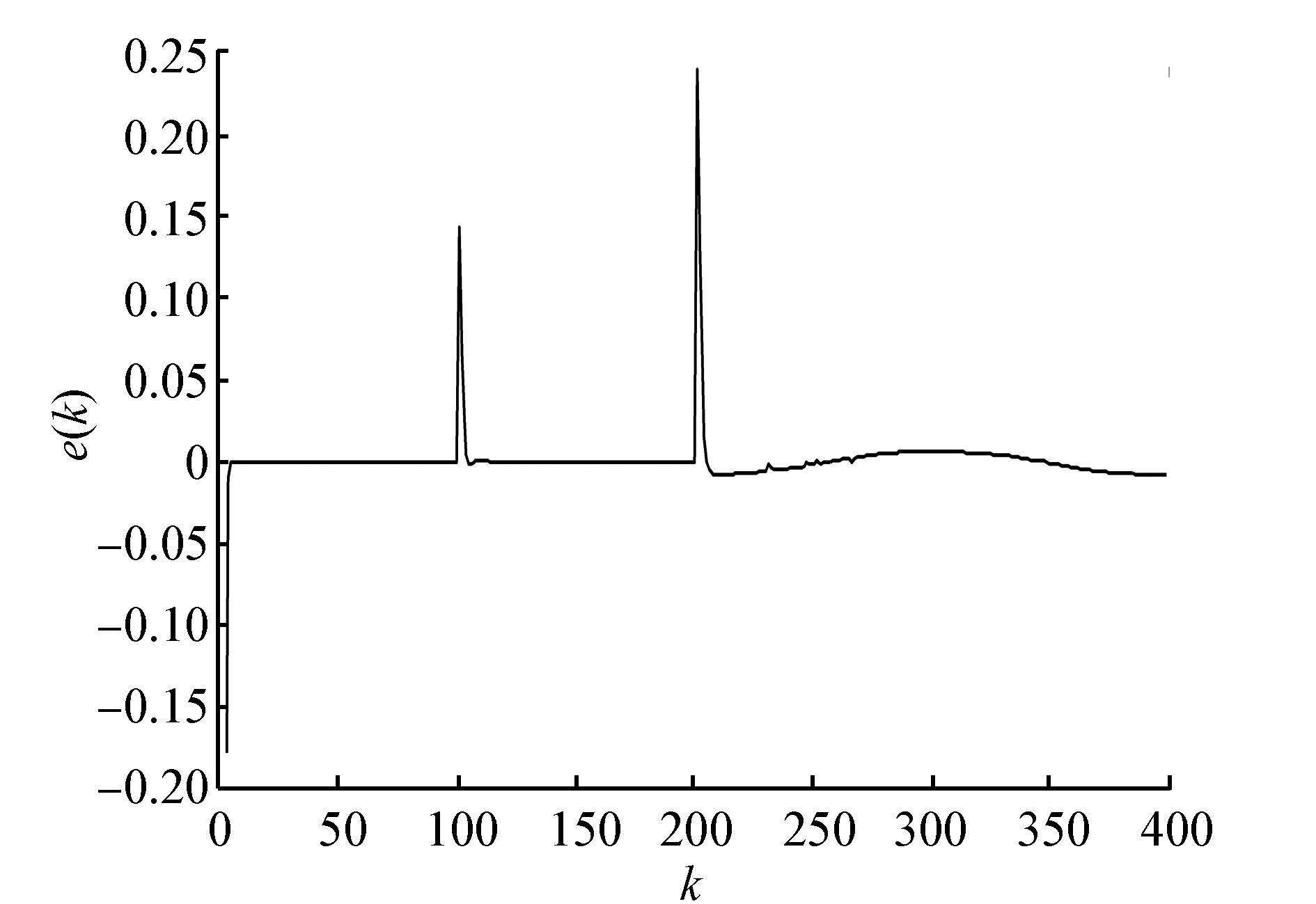
| 图 9 模型2中的跟踪误差信号曲线 Fig. 9 Tracking error curve in model 2 |
|
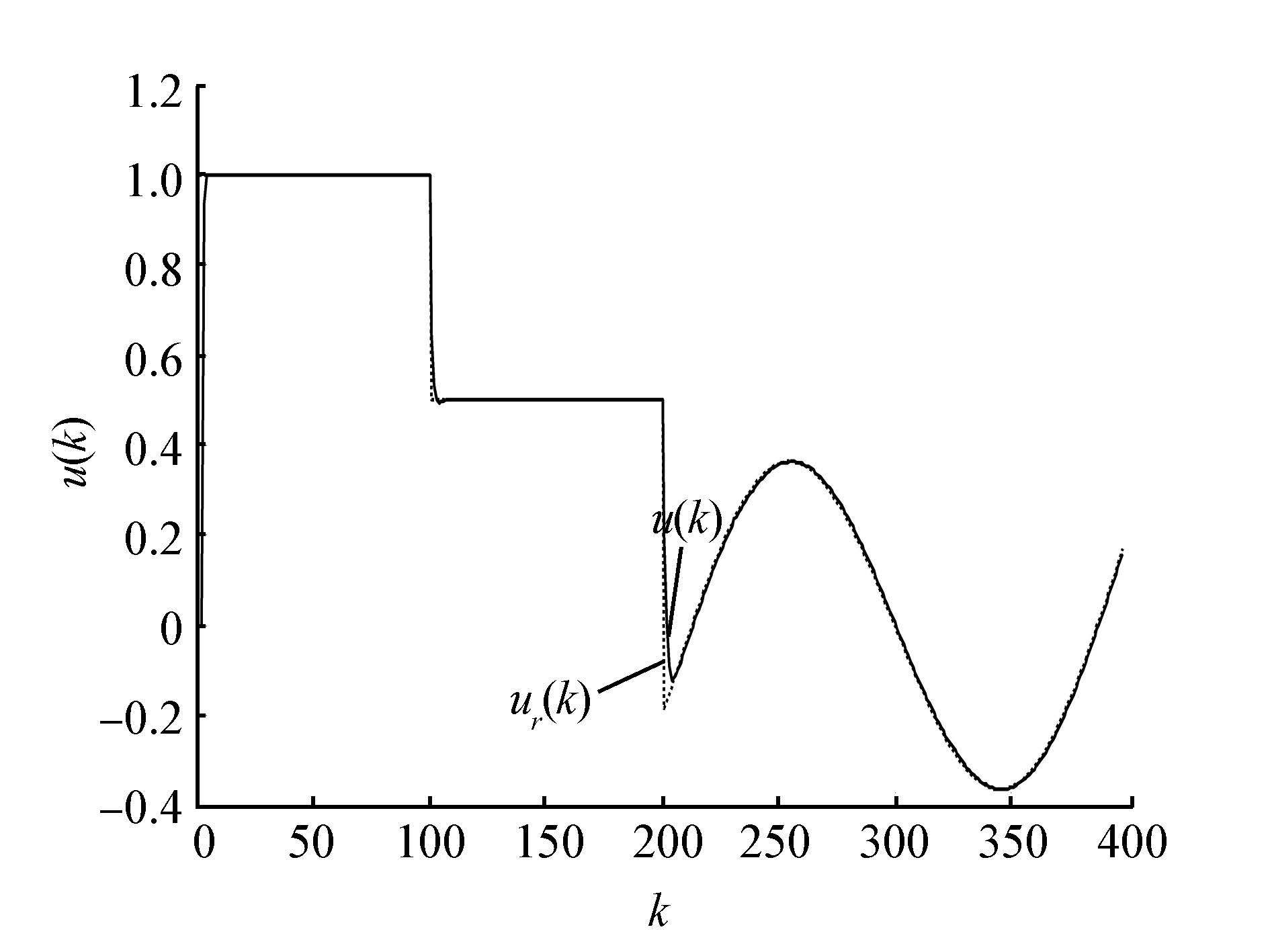
| 图 10 模型2中的控制输入信号曲线 Fig. 10 Control input curve of model 2 |
从以上2个非线性系统模型的仿真结果来看,当参考信号为方波或正弦函数时,通过粒子群算法学习得到Elman无模型控制器的最优网络权值,最后得到的控制量与期望的控制量信号误差较小,并且能很好地实现对模型输出参考信号的实时跟踪,把输出误差控制在合理范围内,具有良好的收敛性。与基于BP网络+BP算法的无模型控制方法相比,拥有较快的响应速度和较好的控制精度。由此证明了基于Elman网络与粒子群算法的无模型控制方法是有效与合理的。
4 结束语本文针对一类单输入单输出离散非线性系统,提出基于Elman网络结构的无模型控制方法,利用粒子群优化算法对控制器的参数进行优化学习,通过两个仿真模型的跟踪控制,结果证明了该方法的有效性。该方法的优点在于:1) 控制器的设计不依赖于被控对象的具体数学模型,依赖的仅仅是系统的输入输出数据;2)控制器网络结构中的参数向量使粒子群算法进行优化,避免了梯度算法中需要求解偏导数的问题,所有参数统一更新学习,简单便捷。
| [1] | 侯忠生, 韩志刚. 非线性系统鲁棒无模型学习自适应控制[J]. 控制与决策, 1995, 10(2):137-142. HOU Zhongsheng, HAN Zhigang. Robust modelless learning adaptive control of nonlinear systems[J]. Control and decision, 1995, 10(2):137-142. |
| [2] | 李秀英, 李桂英, 毛琳, 等. 采用改进粒子群算法的非线性大时滞系统无模型控制[J]. 智能系统学报, 2013, 8(3):254-260. LI Xiuying, LI Guiying, MAO Lin, et al. Model-free control method for a nonlinear system with large time-delay based on IPSO[J]. CAAI transactions on intelligent systems, 2013, 8(3):254-260. |
| [3] | LEE K Y, KO H S, KIM H C, et al. A free model based intelligent controller design and its application to power system stabilization[C]//Proceedings of the IEEE Power Engineering Society Summer Meeting. Seattle, WA, USA, 2000, 4:1985-1989. |
| [4] | SPALL J C, CRISTION J A. Model-free control of nonlinear stochastic systems in discrete time[C]//Proceedings of the 34th IEEE International Conference on Decision and Control. New Orleans, LA, USA, 1995, 3:2199-2204. |
| [5] | CHENG G S. Model-free adaptive (MFA) control[J]. Computing & Control Engineering, 2004, 15(3):28-33. |
| [6] | 刘德荣, 李宏亮, 王鼎. 基于数据的自学习优化控制:研究进展与展望[J]. 自动化学报, 2013, 39(11):1858-1870. LIU Derong, LI Hongliang, WANG Ding. Data-based self-learning optimal control:research progress and prospects[J]. Acta automatica sinica, 2013, 39(11):1858-1870. |
| [7] | ZHANG L, WANG N. Double neuron model-free control for pH processes[C]//Proceedings of 2010 Chinese Control and Decision Conference. Xuzhou, China, 2010:2867-2871. |
| [8] | ELMAN J L. Finding structure in time[J]. Cognitive science, 1990, 14(2):179-211. |
| [9] | LI Xiang, CHEN Zengqiang, YUAN Zhuzhi. Nonlinear stable adaptive control based upon Elman networks[J]. Applied mathematics:a Journal of Chinese universities, 2000, 15(3):332-340. |
| [10] | 王俭臣, 齐晓慧, 单甘霖. 基于EPSO-BP的Elman网络及其在飞行轨迹预测中的应用[J]. 控制与决策, 2013, 28(12):1884-1888. WANG Jianchen, QI Xiaohui, SHAN Ganlin. Elman network based on EPSO-BP and its application in flight trajectory prediction[J]. Control and decision, 2013, 28(12):1884-1888. |
| [11] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Perth, WA, USA, 1995, 4:1942-1948. |
| [12] | 赵勇, 岳继光, 李炳宇, 等. 一种新的求解复杂函数优化问题的并行粒子群算法[J]. 计算机工程与应用, 2005, 41(16):58-60, 64. ZHAO Yong, YUE Jiguang, LI Bingyu, et al. A parallel particle swarm optimization algorithm based on multigroup for solving complex functions optimization[J]. Computer engineering and applications, 2005, 41(16):58-60, 64. |
| [13] | 岑翼刚, 秦元庆, 孙德宝, 等. 粒子群算法在小波神经网络中的应用[J]. 系统仿真学报, 2004, 16(12):2783-2785, 2788. CEN Yigang, QIN Yuanqing, SUN Debao, et al. Application of PSO algorithm in wavelet neural network[J]. Acta simulata systematica sinica, 2004, 16(12):2783-2785, 2788. |
| [14] | 李宁, 邹彤, 孙德宝, 等. 基于粒子群的多目标优化算法[J]. 计算机工程与应用, 2005, 41(23):43-46. LI Ning, ZOU Tong, SUN Debao, et al. Multi-objective optimization utilizing particle swarm[J]. Computer engineering and applications, 2005, 41(23):43-46. |
| [15] | 孙胜永, 胡双演, 李钊, 等. 基于粒子群优化算法的BP神经网络图像复原[J]. 无线电工程, 2014, 44(10):5-7. SUN Shengyong, HU Shuangyan, LI Zhao, et al. BP Neural Network for image restoration based on Particle Swarm Optimization[J]. Radio engineering, 2014, 44(10):5-7. |
| [16] | 金尚泰, 侯忠生, 池荣虎, 等. 侯离散时间非线性系统的数据驱动无模型自适应迭代学习控制[J]. 控制理论与应用, 2012, 29(8):1001-1009.JIN Shangtai, HOU Zhongsheng, CHI Ronghu, et al. Data-driven model-free adaptive iterative learning control for a class of discrete-time nonlinear systems[J]. Control theory & applications, 2012, 29(8):1001-1009. |
| [17] | NARENDRA K S, MUKHOPADHYAY S. Adaptive control using neural networks and approximate models[J]. IEEE transactions on neural networks, 1997, 8(3):475-485. |



