2. 厦门大学福建省仿脑智能系统重点实验室, 福建厦门 361005
2. Fujian Key Laboratory of the Brain-Like Intelligent System, Xiamen University, Xiamen 361005, China
卷积神经网络模型训练过程中存在一个共同的问题,即当模型复杂度比较高时,由于训练数据相对不足而产生过抑合现象,导致模型泛化能力比较差。一系列正则化技术被用来解决该问题,如L1正则化,L2正则化,即对损失函数增加L1范数或L2范数,根据图像变换扩增训练数据等。虽然上述方法可以在一定程度上抑制过拟合,训练出比未正则化模型泛化性更强的模型,但是由于以上方法是基于参数的方法,在解决过抑合问题的同时却增加了模型训练复杂度,在一定程度上弱化了其效果。
Hinton 等[2] 提出的dropout是另外一种正则化方法,它在训练过程中以0.5的概率随机将网络中神经元的响应值置为0。该方法在计算机视觉的多个问题中都取得了不错的成绩,然而目前仍不能完全解释它的有效性。Dropout并不能在神经网络的每一层都提高模型的泛化能力,甚至会起反作用,因此dropout在网络中的位置选择非常重要,然而目前并没有特定的标准,依赖于个人经验。
池化方法是一种无参的正则化方法。极大池化(max pooling)简单地从池化区域中选择最大值作为最终响应值,虽然保留了高频分量,如图像的边缘等信息,但它对噪声信息非常敏感,并且在训练中极易出现过抑合。平均池化(average pooling) 对池化区域的所有值取平均,该方法虽然考虑了区域中所有信息,有效地降低了噪声信息的影响,然而它平滑了图像,从而导致非常重要的高频信息丢失。
为确保模型的判别性及鲁棒性,池化策略必须保留高频分量以提高判别性,同时通过一定的随机性以增强鲁棒性。本文从全新的角度提出了一项卷积神经网络池化策略:矩池化。首先,计算池化区域的中心矩(即图像灰度重心),一般情况下中心矩是一个浮点值,并不指向图像中一个确定的像素位置,本文根据概率随机地从中心矩的4个邻域中选择一个作为最终的响应值。该策略应用中心矩方法在保留高响应值的同时弱化了噪声信息的影响,随机性避免了训练过程中的过抑合现象。
1 卷积神经网络人类的视觉系统对外界的认识是从局部到全局的过程,因而 卷积神经网络(convolutional neural network CNN)认为图像的局部像素联系比较远距离的像素联系更紧密。因此卷积神经网络在高分辨率提取局部特征,然后在低分辨率将局部特征组合形成更加复杂的特征。CNN通过增加较高层特征图的数量来补偿空间信息的丢失。CNN的基础框架由卷积层和池化层组成,卷积层类似于简单细胞,池化层使图像特征具有平移不变性。
1.1 卷积层卷积层是实现图像局部联系的一种途径,它通过参数共享学习适用于所有数据的底层特征。图 1是第一个卷积层学习到通用的边缘特征,更高的卷积层可以提取更加具体的特征如轮廓。卷积层将整个图片与卷积核卷积,然后计算卷积核在图片每个位置的内积,将输出作为特征图c,c可以用来评价图像的每一个部分与卷积核的匹配度。

|
| 图 1 CNN网络第一卷积层学习到的部分边缘特征 Fig. 1 The part of edge features learned by the first convolution layer of CNN |
然后将非线性变换函数应用于特征图c,即: a=f(c)。非线性变换函数f有很多种选择,最常用的是 tanh 和logistic 函数。本文选择受限线性单元 (ReLU)f(c) =max(0,c),V.Nair[3]证明ReLU比tanh和logistic泛化能力更强。
1.2 池化层池化层通过池化函数pool(·)将图像中一个较小的子区域R的信息集合起来,其作用是通过降低分辨率获得模型对图像平移及旋转变换的不变性。

Pool有2种常用函数:max[4]和ave[5]。前者取池化区域的最大值:

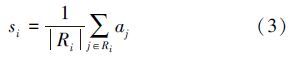
在深度卷积神经网络中,上述2种池化方法都有其不可避免的缺点。由于max 仅简单地选择最大值,因此对噪声非常敏感,并且实验发现该方法极易过抑合。ave考虑了池化区域中所有元素,避免了噪声的影响,然而在CNN中我们期望池化层尽可能保留强响应值,但ave考虑了池化区域中的所有元素,并且赋予了相同权重。当选择ReLU 函数作为非线性变换函数时,ave考虑了大量的0 值,间接地降低了强响应值的权重。假如非线性变换函数选择tanh,ave会抵消掉正负强响应值(梯度方向相反),返回一个完全不具代表性的响应值。
1.3 全连接层全连接层一般在网络的最后几层,与卷积层不同,它感知全局信息,将卷积层学习到的局部特征聚集起来形成全局特征用于特定的图像处理任务,如分类、检测、识别等。
2 矩池化矩不变性是图像处理中一个经典问题,自1962年 H.Ming et.al[6]将矩特征应用于模式识别中后,该方法被广泛应用到计算机视觉中的多个邻域。由于矩特征具有平移不变性、相似变换不变性、旋转不变性以及正交变换不变性,因此它被成功地应用于图像分类中。P.Rosin[7] 认为局部区域的灰度值分布相对于其中心具有偏移性,因此他利用图像中心到中心矩的向量来表示局部区域的主方向。E. Rublee[8]在提取二值特征时,将矩特征应用于估计主方向以提高特征的鲁棒性。本文将中心矩与随机选择结合起来,将其应用于CNN的池化操作中,为了不增加CNN模型的计算复杂性,本文采用一阶矩。
灰度矩定义如下:
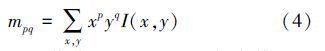
中心矩定义如下:

根据式(4)、(5)计算池化区域的中心矩 c(x,y),一般情况下c为浮点值,不指向任何一个确定的离散值,如图 2所示,其上下边界具有4个确定位置(Q11 ,Q12 ,Q22,Q21),称其为c的四邻域。在图像放大中采用插值法计算插入点的像素值,本文借鉴该思想通过中心矩的四邻域计算其响应值。


|
| 图 2 矩池化选择方法 Fig. 2 The moment pooling’s selection strategy |
最近邻插值法[9]选择与插入点最近的像素作为中心矩的像素值,虽然该方法插值速度快,但它容易出现棋盘格效应。且在池化操作中,中心矩与最大值像素位置非常接近,最近邻插值法几乎等价于极大池化法。
双线性插值法[10]用待插入点的2×2区域的4个邻近像素的值通过加权平均计算得到。其核心思想是在x、y方向上分别进行一次线性插值,距离待插入点越近,权值越高。在池化操作中双线性内插算法不会出现像素值不连续的情况,然而此算法和平均池化类似,具有低通滤波器的性质,使高频分量受损,所以可能会使轮廓信息在一定程度上变得模糊。除此之外,双线性插值法要分别在2个方向上插值,增加了模型的计算复杂度。
本文在2个方向上以概率px、py随机选择x、y,式(7)、(8)所示距离中心矩越近,被选择的可能性越大。最后根据选择的(x,y) 坐标从四邻域中选择池化区域的响应值。矩池化的随机性使每次选择都不相同,因此可以有效地达到预防过抑合的效果。在计算复杂度上,该策略只需要随机生成2个概率,远小于双线性插值法,与最近邻插值法接近。p1=(x2-x)

实验部分将矩池化、极大池化、平均池化分别在MNIST,CIFAR-10,CIFAR-100数据集上进行比较,图 3代表3个数据集的部分数据。实验采用深度学习框架caffe[11],caffe是一个清晰而高效的深度学习框架,它具有上手快、速度快、模块化、开放性及社区好的特点,并且支持命令行、python和matlab接口,可以在CPU和GPU 间无缝切换,大大提高了模型的学习效率。

|
| 图 3 实验中用到的部分数据 Fig. 3 The part experiments data |
模型优化采用随机梯度下降法(stochastic gradient descent),通过损失函数的负梯度∇L(Wt)与t时刻权重更新值vt的线性组合来更新权重。 学习率α代表负梯度的权重,势μ代表vt的权重。形式上,在给定t时刻的vt、wt时,通过式(9)更新t+1时刻的权重。这两个参数需要通过调整来得到最好的结果[12],一般经过 stepsize 个训练回合,将α更新为原来的γth。
训练中需要优化的参数有训练的回合数(epcho),学习率α,势μ,权重衰减λ,α的变化步长 stepsize和变化率γ,本文中μ=0.9 ,γ=0.01,其他参数设置与具体任务有关。

CIFAR-10[13]包含6万个32×32的RGB图片,共分为10 种类型。训练数据50 000 张图片,测试数据10 000 张图片。实验采用Hinton等提出的dropout模型2,该模型包含3个卷积层,每个卷积层由64个5×5的卷积核构成,卷积层将非线性变换函数ReLU的结果作为它的输出。池化层选择大小为3的池化区域,以步长为2实施池化操作,然后通过局部响应归一化层(LRN:local response normalization)对池化结果进行局部归一化以抑止非常大的ReLU的输出值。最后一层是全连接层,它的softmax输出是整个网络的分类预测结果。
实验中α的调整步长stepsize的大小非常重要,其太小将会导致模型迟迟不能跳出局部最优;反之由于学习率太大,模型一直在全局最优附近徘徊,前者会降低模型泛化能力,后者延缓了模型的训练速度。图 4是stepsize=20 、100 时矩池化的误差曲线,第一次学习率调整后,误差曲线都会加速下降。后续调整仅降低训练误差,对测试误差影响甚微,因此最大迭代次数不超过2×stepsize。由图 4可看出选1.2~1.5倍即可。当stepsize =20时,曲线仍保持比较大的下降趋势,即模型还未达到全局最优附近,此时降低学习率,使模型在后面的迭代过程中极易陷入局部最优,测试误差为20.57%;当stepsize=100时,曲线变化已趋平缓,此时降低学习率可使模型趋于全局最优,测试误差降低至17.24%,后续实验参数设置如表 1所示。

|
| 图 4 学习率α的迭代步长对实验结果的影响 Fig. 4 The effect of learning rate to α’s iteration stepsize |
| epoch | α | stepsize | γ | λ |
| 120 | 0.001 | 100 | 0.01 | 0.004 |
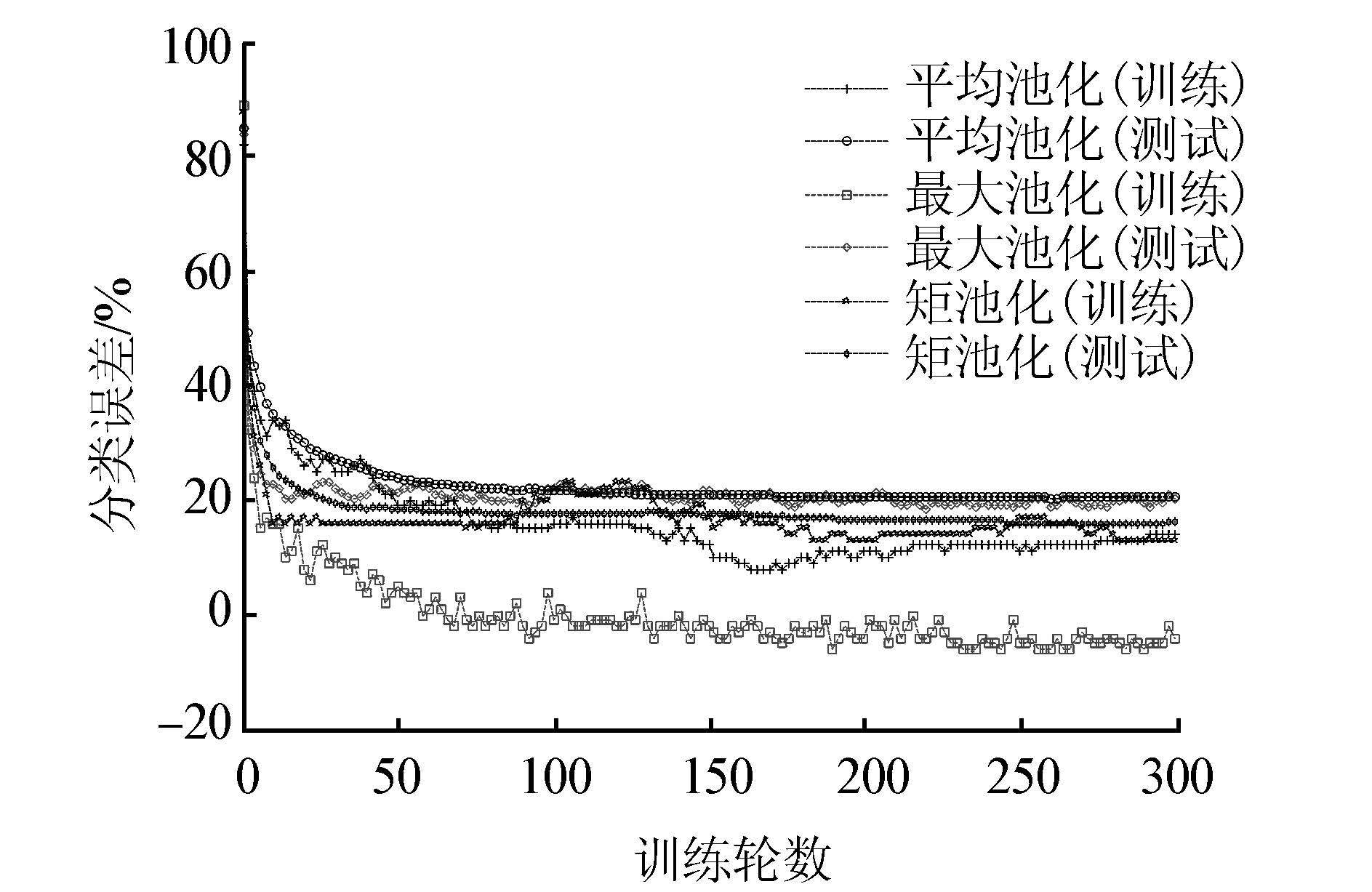
使用上述CNN模型,在池化层分别采用极大池化,平均池化以及本文提出的矩池化方法,并比较它们的分类结果。如图 5所示,最大池化曲线训练过程中快速下降到0,平均池化的训练误差及测试误差都比较高。矩池化在有效避免过抑合的同时,又能保证最低的预测误差,这与矩特征的2个特性息息相关。表 2比较3种池化方法在CIFAR-10数据集上的训练误差及预测误差,矩池化预测误差最低。
|
| 图 5 数据集CIFAR-10上的实验结果 Fig. 5 Experiments result on dataset CIFAR-10 |
| 方法 | 训练误差/% | 预测误差/% |
| 平均池化 | 10.40 | 19.11 |
| 最大池化 | 0.00 | 19.38 |
| 矩池化 | 6.00 | 17.24 |
MNIST[14]由大小为28×28的手写体0~9组成,数据集中包含60 000张训练图片和10 000张测试数据,实验中预处理时将图片归一化到[0,1]。
Lecun Y[15]提出的LeNet-5模型在数字分类任务中取得了非常好的效果,本文采用的模型与LeNet-5略有不同,将原来的非线性变换函数sigmoid替换为ReLU。实验中参数设置如表 3所示,stepsize=fixed 表示学习率在学习过程中不变,实验中为20。
| epoch | α | stepsize | γ | λ |
| 100 | 0.01 | fixed | null | 0.000 5 |
训练过程中,3种池化方法几乎都完全过度抑合训练数据,权重衰减虽然可以预防过抑合,但在该数据集上效果甚微,表 4比较各个池化方法在MNIST数据集上的结果。矩池化方法只是一种正则化方法,因此可以与其他方法结合提高模型泛化能力。
| % | ||
| 方法 | 训练误差 | 预测误差 |
| 平均池化 | 0.05 | 1.51 |
| 最大池化 | 0.02 | 1.07 |
| 矩池化 | 0.10 | 0.93 |
CIFAR-100[8]数据集与CIFAR-10类似,不同之处在于它增加了图片类别数到100,包含50 000张训练数据(每类500张)及10 000张测试数据。CIFAR-100的训练模型以及参数设置如表 5所示,与CIFAR-100的基本一致,为提高准确率将第3个卷积层数增加到128。相较于CIFAR-10,CIFAR-100的训练数据相当有限,而模型却更加复杂。如表 6所示有限的训练数据下传统的池化方法并没有很好的泛化能力,而矩池化方法有效地降低了分类误差。
| epoch | α | stepsize | γ | λ |
| 300 | 0.001 | 100 | 0.01 | 0.004 |
| % | ||
| 方法 | 训练误差 | 预测误差 |
| 平均池化 | 27.00 | 47.03 |
| 最大池化 | 1.00 | 49.64 |
| 矩池化 | 14.00 | 45.38 |
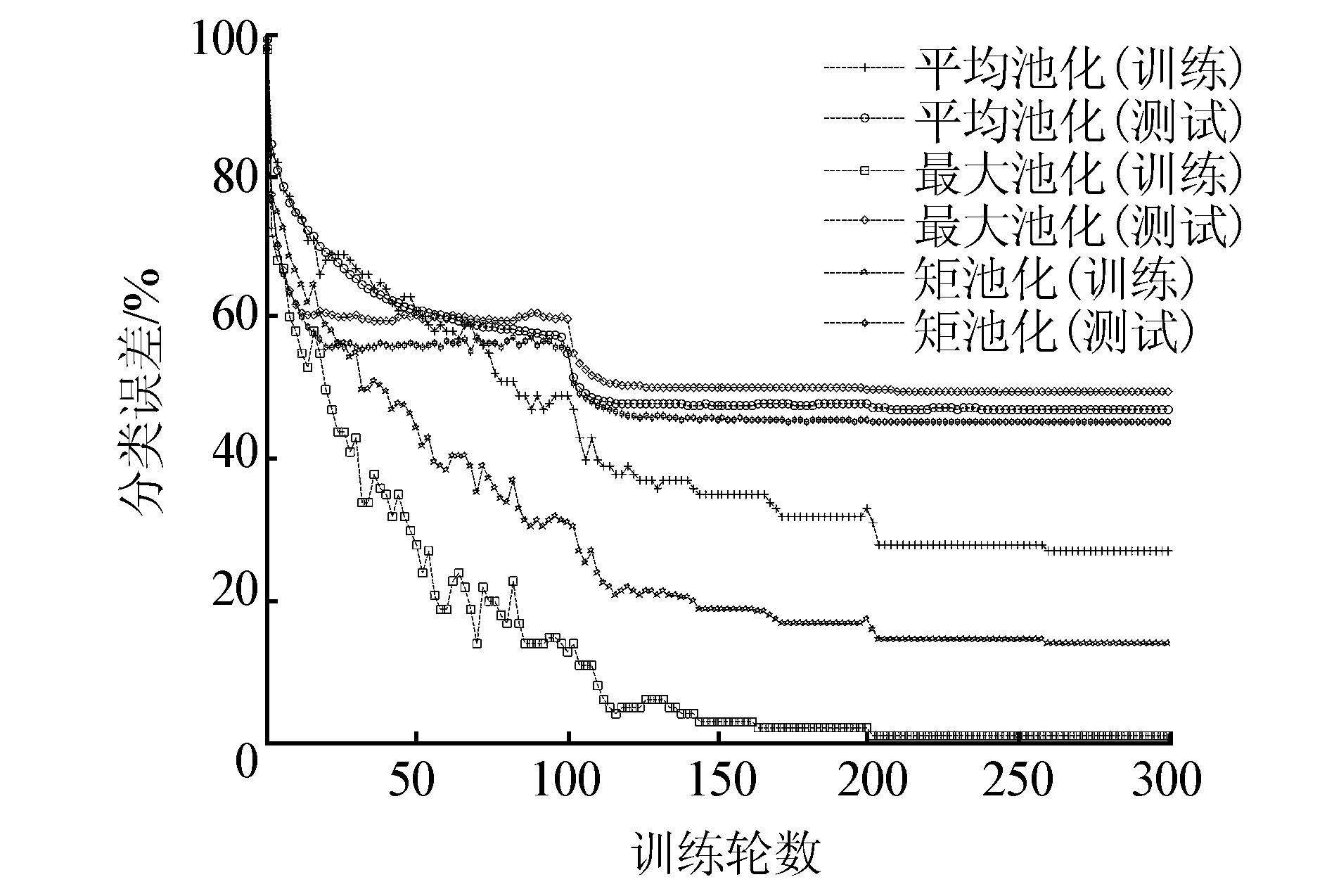
数据集CIFAR-100上的实验结果如图 6所示,可以看出,第1次调整学习率前,曲线已趋平缓,调整后曲线迅速下降,与CIFAR-10 实验结果一致。
|
| 图 6 数据集CIFAR-100上的实验结果 Fig. 6 Experiments result on dataset CIFAR-100 |
本文在卷积神经网络的框架上提出了一种可以与其他正则化方法结合使用的池化策略,如dropout、权重衰减、数据扩增等。矩池化将中心矩与随机选择应用于CNN的池化层中,中心矩选择池化区域的灰度重心而非最大值,在保持模型判别性的同时有效地消除噪声的影响;而选择的随机性,使每次选择具有一定的不确定性,从而更好地避免过抑合,提高模型鲁棒性。除此之外,矩池化是一种无参的正则化方法,不会影响模型复杂度,可以与任何已有的CNN模型相结合。实验表明该方法可以有效地预防过抑合,提高模型的泛化能力。
| [1] | MONTAVON G, ORR G, MÜLLER K R. Neural networks:tricks of the trade[M]. 2nd ed. Berlin Heidelberg:Springer, 2012. |
| [2] |
HINTON G E, SRIVASTAVE N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[EB/OL].http://arxiv.org/pdf/1207.0580.pdf. [3] NAIR V, HINTON G E. Rectified linear units improve restricted boltzmann machines[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel, 2010.[2012-07-03]. |
| [4] | RANZATO M, BOUREAU Y L, LECUN Y. Sparse feature learning for deep belief networks[C]//Proceedings of Advances in Neural Information Processing Systems (NIPS). Cambridge, MA, 2007. |
| [5] | LECUN Y, BOSER B E, DENKER J S, et al. Handwritten digit Recognition with a back-propagation network[C]//Proceedings of Advances in Neural Information Processing Systems (NIPS). Cambridge, MA, 1989. |
| [6] | HU M K. Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theory, 1962, 8(2):179-187. |
| [7] | ROSIN P L. Measuring corner properties[J]. Computer vision and image understanding, 1999, 73(2):291-307. |
| [8] | RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB:an efficient alternative to SIFT or SURF[C]//Proceedings of IEEE International Conference on Computer Vision (ICCV). Barcelona, 2011:2564-2571. |
| [9] | EVANS O D, KIM Y. Efficientimplementation of image warping on a multimedia processor[J]. Real-time imaging, 1998, 4(6):417-428. |
| [10] | GONZALEZ R C, WOODS R E. Digital image processing[M]. 2nd ed.New Jersey:Prentice-Hall, 2002. |
| [11] | JIA Y, SHEHAMER E, DONAHUE J,et al.Caffe:convolutional architecture for fast feature emibedding[C]//Proceedings of the ACM International conference on Multimedia. ACM, 2014:625-678. |
| [12] | BOTTOU L. Stochastic gradient descent tricks[M]//MONTAVON G, ORR G B, MÜLLER K R. Neural Networks:Tricks of the Trade. 2nd ed. Berlin Heidelberg:Springer, 2012:421-436. |
| [13] |
KRIZHEVSKY A. The CIFAR-10, CIFAR-100 database[EB/OL]. http://www.cs.toronto.edu/-kriz/cifar.html. LECUN Y, CORTES C, BURGES C J C.http://yann.lecun.com/exdb/mnist/. [14] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11):2278-2324. The MNIST database of handwritten digits[EB/OL]. |



