2. 南开大学 智能机器人技术天津市重点实验室, 天津 300350;
3. 中国民航大学 理学院, 天津 300300
2. Key Laboratory of Intelligent Robotics of Tianjin, Nankai University, Tianjin 300350, China ;
3. College of Science, Civil Aviation University of China, Tianjin 300300, China
自20世纪初飞机问世以来,航空运输系统飞速发展。与其他运输方式相比,航空运输具有及时、高效、灵活的优势,尤其是在长距离运输和国际客运方面的重要作用日益凸显[1]。航空运输系统是一个易受环境影响的开放的复杂系统,随着系统规模的不断扩大,它在带给人们便利的同时也带来了一系列的问题。航班延误已经成为人们司空见惯的现象,于是,在自然灾害或人为因素导致航班不能正常起降的突发情况下,航空运输系统能够保持其鲁棒性,成为人们越来越关注的问题。
刘宏鲲等[2]研究表明,中国城市航空网络具有较大的聚类系数和较短的平均路径长度,其度分布服从双段幂律分布,是一个具有小世界网络特性的无标度网络; 姚红光等[3]通过仿真实验得出,中国航空网络在面对随机干扰时鲁棒性较强,而在蓄意攻击下鲁棒性较差;不同的城市节点对于网络鲁棒性的贡献程度不同,目前有40余个核心城市在中国航空网络中占有举足轻重的地位。
航空网络中,准确地评估和度量节点的重要性在提高网络的可靠性与抗毁性方面扮演着非常重要的角色。在由城市节点和通航城市间的直飞航线所构成的航空网络中,如果受突发事件的影响,某城市节点陷入瘫痪,那么这就意味着同时取消了与该城市节点相连的所有的航线,从而有可能引发网络中其他通航城市之间的一些运输路径中断[4]。例如,2015年7月11日,超强台风“灿鸿”逼近上海,受台风“灿鸿”影响,上海机场终端区的通行能力下降50%左右,共计取消航班300多个架次。因此,准确评估航空网络中的重要节点,并针对其可能发生的突发状况提前制定完备的候选方案和补救措施,可以有效避免网络因受到外界干扰而造成航班大面积延误,从而保证航空运输安全高效地运营。
1 理论基础将航空网络抽象为一个由点集V=[v1 v2 … vn]和边集E=[e1 e2 … em]组成的无向图G=[V E],顶点数记为N=|V|,边数记为M=|E|。图的邻接矩阵记为An×n=(aij),当且仅当节点vi与vj之间有连边时aij=1,否则aij=0。
定义1 无向网络中节点vi的度ki是指与节点直接相连的边的数目。它与节点的重要程度有很大的关系。一般而言,ki的值越大,节点就越重要。其表达形式为
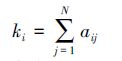 |
定义2 节点距离定义为连接这两个节点的最短路径上的边的数目,用dij表示。
定义3 网络的平均路径长度L定义为任意两个节点之间距离的平均值,即
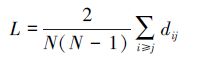 |
定义4 网络中一个度为ki的节点vi的聚类系数C(i)定义为
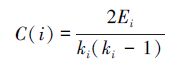 |
式中:Ei是节点vi的ki个邻节点之间实际存在的边数,即节点vi的ki个邻节点之间实际存在的邻居对的数目。聚类系数表征在网络中某一节点的两个相邻节点也相邻的概率,反映的是网络的集聚化程度。
2 无向网络节点重要性指标在复杂网络领域里评价节点重要性的方法有很多,本质上都是源于图论和基于图的数据挖掘,主要分为以下3类:社会网络分析、系统科学分析、信息搜索领域分析[5]。其本质上都是源于图论以及基于图的数据挖掘,主要从网络拓扑结构入手进行分析。
社会网络分析方法起始于20世纪40年代末,在评价节点重要性的研究领域中是比较常见的。它主要基于这样一种假设:“重要性等价于显著性”,即节点的重要性等价于该节点与其他节点的连接而使其具有的显著性[6]。该方法主要以网络的拓扑结构为切入点,在不破坏网络连通性的前提下对重要节点进行研究,并且通常不考虑节点集的重要性[7]。通过分析网络中的某种有用信息来区分不同节点的重要性差异,其主要的分析指标包括节点的度 (degree)、接近度(closeness)、介数(betweenness)、特征向量(eigenvector)等。
2.1 度中心性度中心性(degree centrality)[8],就是按照度值的大小对节点进行排列。它是网络中刻画节点重要性最简单而又非常重要的指标。具有相同度值的节点在不同规模的网络中的重要程度是不同的,因此为了便于比较,将节点的度中心性进行归一化处理:
 |
显然,度中心性描述的是节点对于其邻居节点的直接影响力,它认为一个节点的度值越大,与之有直接联系的邻居就越多,也就越重要[9]。这种方法简单直观,计算的复杂度低,但是它仅仅考虑了节点的最局部的信息,具有非常大的片面性,没有办法准确地刻画网络中节点的重要程度。例如,“桥节点”虽然只有两条边相连,但是在网络中处于重要的核心地位。
2.2 接近中心性接近中心性(closeness centrality)[10]反映的是节点在网络中居于中心的程度。它的基本思想是如果一个节点能很容易地与所有其他节点进行互动,那么它就处在网络的中心位置,也就是说它到其他所有节点的距离要足够短。因此,接近中心性可以用最短距离来刻画。假设节点vi和vj之间的最短距离记为dij,则可以计算任意一个节点vi到网络中其他节点的平均最短距离:
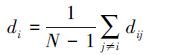 |
于是节点vi的接近中心性定义为di的倒数,即:
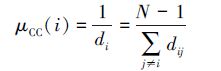 |
(1) |
该定义只能在连通的网络中使用,因此文献[11]对上式进行了改进,使其能够用于非连通网络中,即:
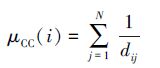 |
如果节点vi和vj之间没有路径可达,则定义dij=∞,即1/dij=0。
由上式可知,节点的接近中心性越大,表明该节点越接近网络的中心位置,那么它在网络中就越重要。这一类节点与其他节点的联系并非最多,但是与网络中其他节点的距离总和最短,也就是该节点在网络中具有最佳视野,可以察知网络中所发生的事情以及信息的流通方向。与前面的度中心性相比,接近中心性更能反映网络的全局结构,但是这种方法的计算复杂度较高,并且对网络的拓扑结构具有依赖性,例如它可以准确地发现星形网络结构的中心节点,但是并不适用于随机网络。
2.3 介数中心性介数中心性[12](betweenness centrality)一般是指最短路径介数中心性(shortest path BC)。简单地讲,它刻画了节点对网络中沿最短路径传输的网络流的控制力,很好地描述了网络中节点可能需要承载的流量。
节点vi的介数定义为
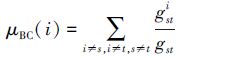 |
式中:gst代表从节点vs到vt的所有最短路径的数目,gsti代表从节点vs到vt的gst条最短路径中经过vi的最短路径的数目。在包含n个节点的连通网络中,一个节点的介数最大可能取值为星形网络中心节点的介数值,即(n-1)(n-2)/2。于是可以对节点vi的介数进行归一化处理:
 |
节点的介数值越高,表明流经它的网络流越多,那么这个节点就越有影响力。与此同时,这也意味着该节点更容易发生拥塞,成为网络的瓶颈。介数中心性能够非常准确地找到网络中“流量”大的节点,但是它的时间复杂度为O(N3),计算效率低,对于大型的网络并不适用。
2.4 特征向量中心性特征向量中心性(eigenvector centrality)[8]是评价网络中节点重要性的一个重要指标。前面介绍的几种方法把周围的邻居节点视为同等重要,仅仅从邻居节点的数量上来考虑节点的重要性。而特征向量中心性同时兼顾了邻居节点的数量和质量对节点重要性的影响,认为一个节点的重要性不仅取决于该节点邻居的数量,而且取决于每个邻居节点的重要程度。特征向量中心性指标是指网络邻接矩阵对应其最大特征值的特征向量,即:
 |
式中:λ为邻接矩阵 A的最大特征值, e=[e1 e2 … en]T为邻接矩阵A的最大特征值λ对应的特征向量。
2.5 半局部中心性在以上提出的几种方法中,度中心性虽然简单直观,计算的复杂度低,但只考虑了局部信息,并不能准确刻画节点的重要程度。介数中心性和接近中心性等基于全局信息的指标,虽然能够准确的定义重要节点,但是由于其计算的复杂性,不能应用于大规模的复杂网络。为了兼顾算法的准确度和计算效率,Chen[13]等选取网络中节点的四阶邻居信息,提出了基于半局部信息的节点重要性排序方法,称为半局部中心性(semi-local centrality)。
半局部中心性μSLC(i)定义为
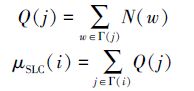 |
式中:Γ(j)表示节点vj的一阶邻居节点的集合,N(w)指从vw出发两步内可以到达的邻居的数目,称为节点vw的两层邻居度。
相比于度中心性的一阶邻居信息,半局部中心性考虑了节点的四阶邻居信息,因此其准确性比度中心性更好。于此同时,计算N(w)只需要遍历节点vw的两层邻居节点,因此其计算的复杂度相较于介数中心性和接近中心性更低。
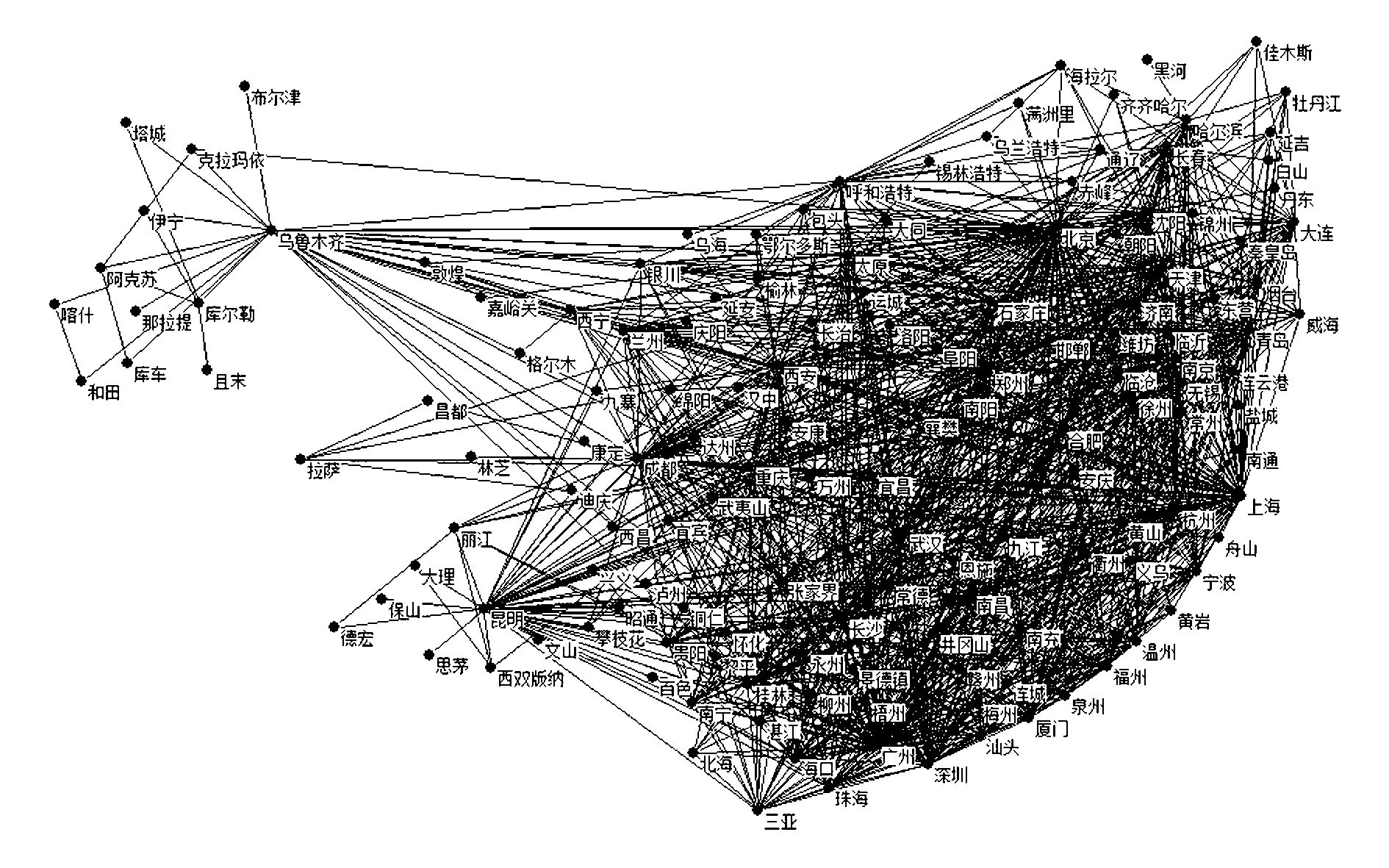
3 中国航空网络重要性节点分析 3.1 网络构建与结构特性以中国民用航空局官方网站公布的夏秋航季客运航线相关数据为样本构建中国航空网络模型,其中机场所在的城市为网络节点,通航城市之间的直飞航线为网络的边。这样形成了148个节点,1 153条无向边(2 306条航线)的中国航空网络(见图 1)。将中国航空网络用一个148×148的邻接矩阵A表示,如果节点vi和vj之间有可达的航班,则aij=1;反之aij=0,于是得到一个对称矩阵。
|
| 图 1 中国航空网络结构图 Fig. 1 The structure of Chinese aviation network |
在此需要说明的是:
1) 网络中所选的航线均为往返航线,因此在后期运算过程中不需要考虑航线的方向问题;
2) 对于拥有两个及以上机场的城市,将其数据进行合并,如上海的浦东机场和虹桥机场的数据可统一合并成到城市节点“上海”中。
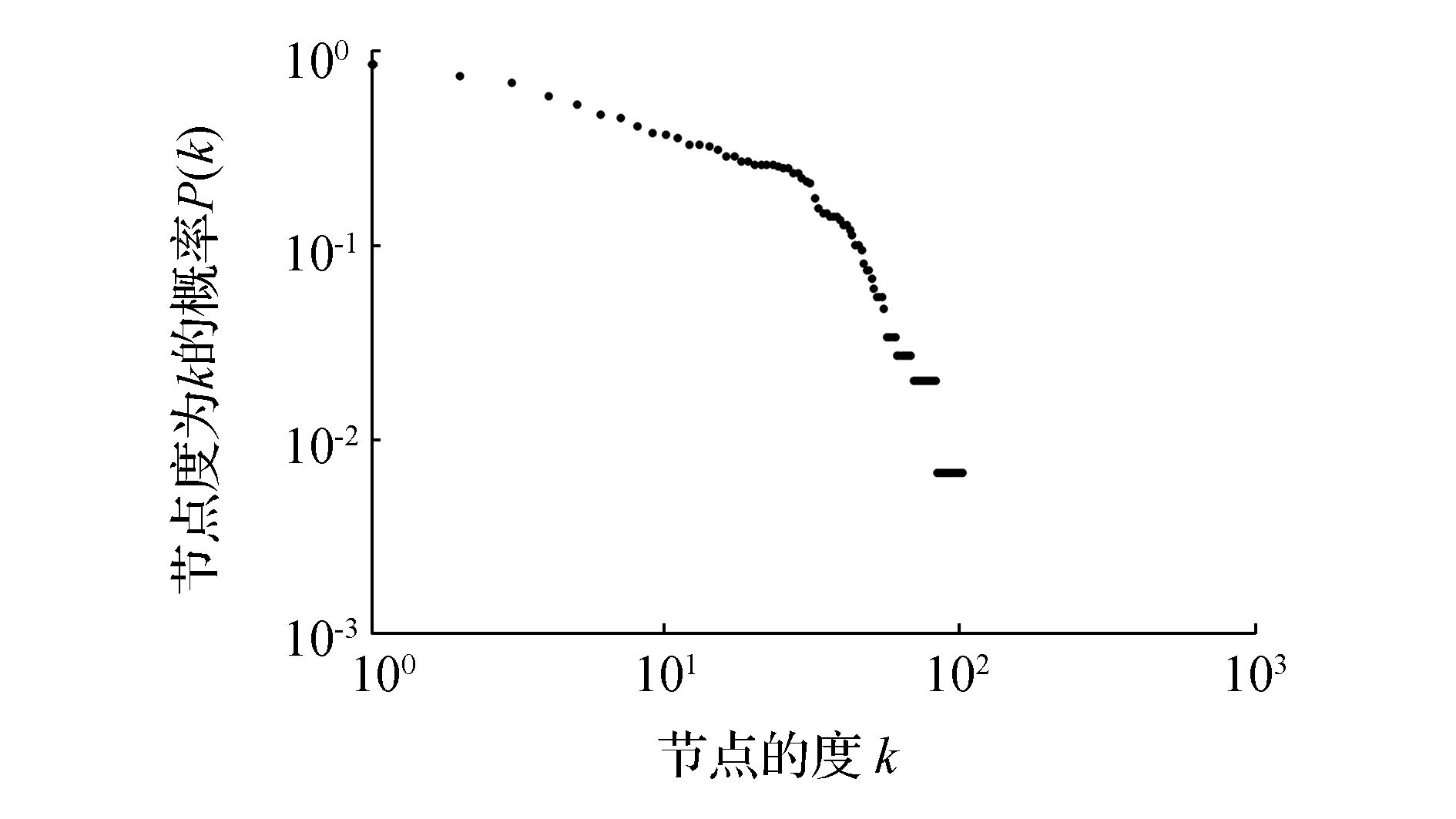
节点的度、平均路径长度和聚类系数是描述复杂网络拓扑结构最基本的特征参量。本文使用的中国航空网络样本,平均度为15.58,也就是说平均每个城市机场约与其他16个城市有直接的航空联系;Pearson相关系数[14]r=-0.384 3,说明中国航空网络是度—度负相关的,度值大的节点更倾向于和度值小的节点相连接。平均路径长度为2.216 5,意味着任意两个城市机场通过不到2次转机就可以相互连通;聚类系数为0.687 7,表现出较强集聚性,说明中国航空网络各节点城市之间更倾向于形成短距离的联系[15]。由此可见,中国航空网络具有较大的聚类系数和较小的平均路径长度,表现出了小世界网络特性。而图 2表明,中国航空网络服从双幂律分布,具有无标度特性。
|
| 图 2 中国航空网络城市节点度分布 Fig. 2 Degree distribution of Chinese aviation network |
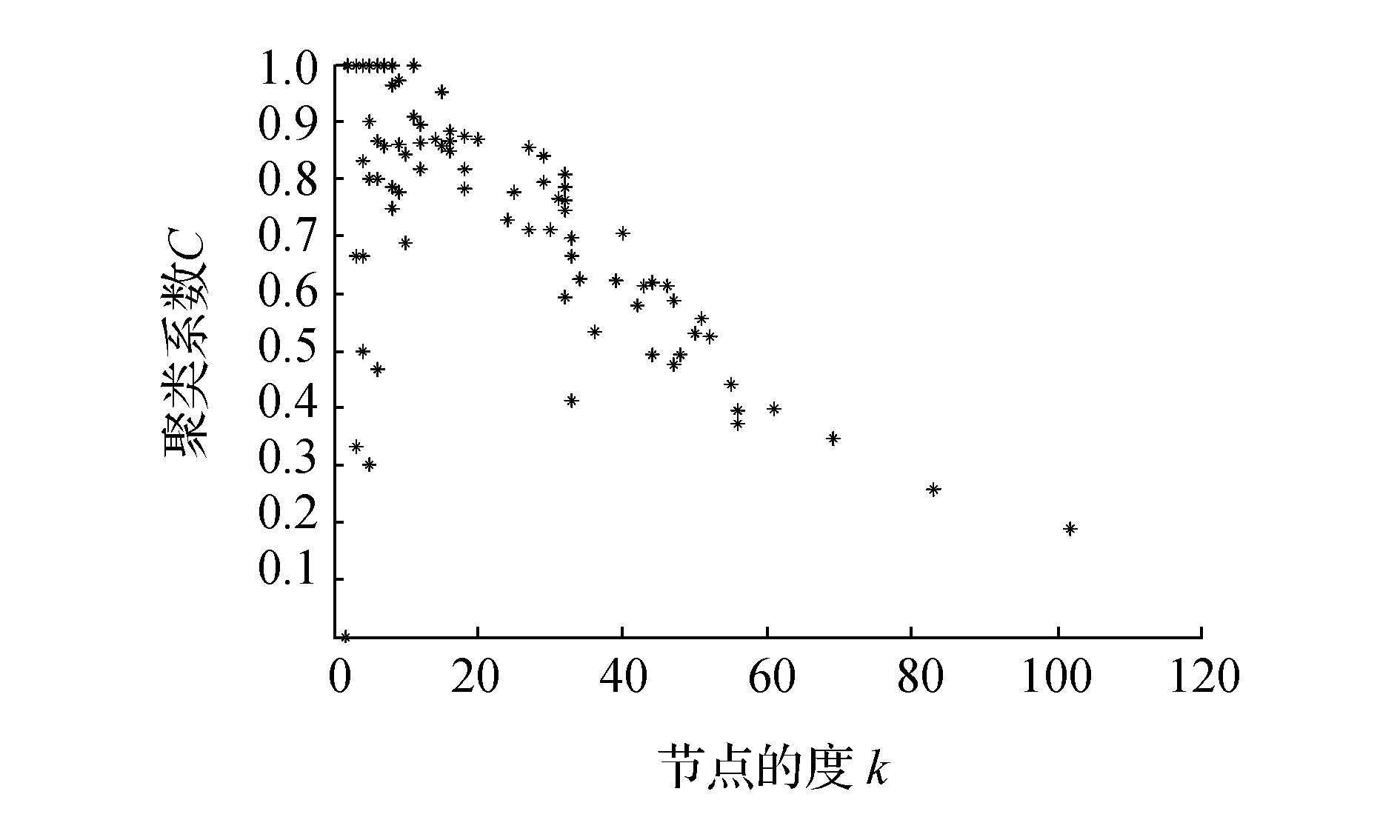
中国航空网络城市节点度与聚类系数相关性如图 3所示。可以看出,随着节点度值k的不断增加,聚类系数C(k)的数值是不断下降的,也就是说节点的度和聚类系数呈负相关。这说明在中国航空网络中,度值小的城市节点比度值大的城市节点更趋向于聚集成团。
|
| 图 3 中国航空网络城市节点度与聚类系数相关性 Fig. 3 Correlation between degree and clustering coefficient of Chinese aviation network |
下面用本文中提到的几种无向网络节点重要性评价指标中国航空网络模型的节点重要程度进行排序,排序结果见表 1。
节点的度反映了该机场与其他机场通航能力的大小。中国航空网络的度分布呈现出明显的东西差异,结合中国航空网网络的空间结构,从表 1中可以看出,度值较大的节点主要集中东部较发达地区,如北京 (102)、上海(83)、广州(83)、深圳(69)、杭州(52)、南京(51)以及各个省会城市,如成都(61)、西安(56)、昆明(56)、重庆(56)。
接近中心性是用网络中的节点到其他节点的平均最短距离来衡量的,因此接近中心性越小,意味着该节点在网络中越处于中心地位,从而也就越不容易受到其他结点连通情况的控制。也就是说,接近中心性数值较大的机场相对于数值较小的机场独立性更强,不太容易受到其他机场通航状况的影响。而接近中心性Top10的节点排序结果基本上跟度中心性保持一致,都表现出明显的东西差异,这一点在特征向量中心性和半局部中心性中都有所体现。
节点的介数中心性反映了该机场在网络运输中的中转和衔接能力。介数中心性高的节点在地区网络间的连接中起到了桥梁的作用。中国航空网络节点的介数中心性排序中,北京依然排在第1位,但是排在第2位的乌鲁木齐在其他排序结果的前十中从未出现过,排在第3位的昆明只在度中心性排序中排在第七位。从空间结构上可以看出新疆地区的城市节点大多数通过乌鲁木齐与整个航空网络连接,若移除乌鲁木齐,则新疆地区的大部分城市节点将变为孤立节点,而昆明也同样起到非常重要的桥梁作用。
| 次序 | 城市 | 度中心性 | 城市 | 接近中心性 | 城市 | 介数中心性 (×103) |
城市 | 特征向量 中心性 |
城市 | 半局部中心性 (×106) |
| 1 | 北京 | 0.694 | 北京 | 0.762 | 北京 | 4.475 | 北京 | 0.220 | 北京 | 0.281 |
| 2 | 上海 | 0.565 | 上海 | 0.693 | 乌鲁木齐 | 2.835 | 广州 | 0.207 | 广州 | 0.268 |
| 3 | 广州 | 0.565 | 广州 | 0.693 | 昆明 | 2.353 | 上海 | 0.207 | 上海 | 0.267 |
| 4 | 深圳 | 0.470 | 深圳 | 0.650 | 广州 | 2.231 | 深圳 | 0.196 | 深圳 | 0.257 |
| 5 | 成都 | 0.415 | 成都 | 0.628 | 上海 | 2.223 | 成都 | 0.184 | 成都 | 0.245 |
| 6 | 西安 | 0.381 | 西安 | 0.615 | 成都 | 1.565 | 南京 | 0.180 | 南京 | 0.242 |
| 7 | 昆明 | 0.381 | 重庆 | 0.610 | 西安 | 1.508 | 杭州 | 0.178 | 杭州 | 0.240 |
| 8 | 重庆 | 0.374 | 杭州 | 0.603 | 深圳 | 1.121 | 重庆 | 0.174 | 重庆 | 0.233 |
| 9 | 杭州 | 0.354 | 南京 | 0.603 | 重庆 | 0.825 | 长沙 | 0.172 | 长沙 | 0.232 |
| 10 | 南京 | 0.347 | 长沙 | 0.598 | 长沙 | 0.790 | 郑州 | 0.170 | 郑州 | 0.231 |
3.3 用网络的鲁棒性和脆弱性评价排序算法
利用之前的节点重要性评价方法对中国航空网络的重要节点进行排序之后,分别按照节点的重要性从大到小的顺序,依次删除网络中的节点。则节点移除后网络的破坏程度可以用最大连通子图的相对大小,全局效率以及脆弱性指标来进行评价。
最大连通子图概念的提出,是为了描述网络中的节点或连边由于一些内部或外部的原因所发生的变化。简单来说,最大连通子图就是一个网络的众多连通子图中包含节点最多的那个子图。
网络中,节点vi和vj之间的效率为两点之间最短距离的倒数,即1/dij。于是网络的全局效率[16]就定义为所有节点对效率的平均值,即
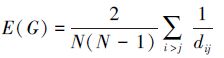 |
如果用i/n表示移除的节点比例,用σ(i/n)表示移除i/n比例的节点后最大连通子图的相对大小,则该节点移除方式下网络的鲁棒性(robustness)可以用R-指标 [17]来评价。具体定义为
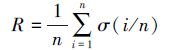 |
显然,无论针对哪种算法都能得到如下结果
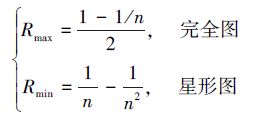 |
所以在任何网络中,无论用何种算法移除节点,R∈(0,1/2)。因此,文献[18]定义V-指标来衡量网络对所实施的节点移除方法的脆弱性(vulnerability)。
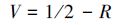 |
可见,脆弱性指标的值越大,表明采用的攻击方法效果越好。于是,分别采用度中心性、接近中心性、介数中心性、特征向量中心性和半局部中心性5种方法对中国航空网络进行攻击,画出i/n和σ(i/n)在二维坐标上的曲线,并用脆弱性指标考察这5种方法的攻击效果,同时与随机攻击网络的方法得到的效果进行比较。
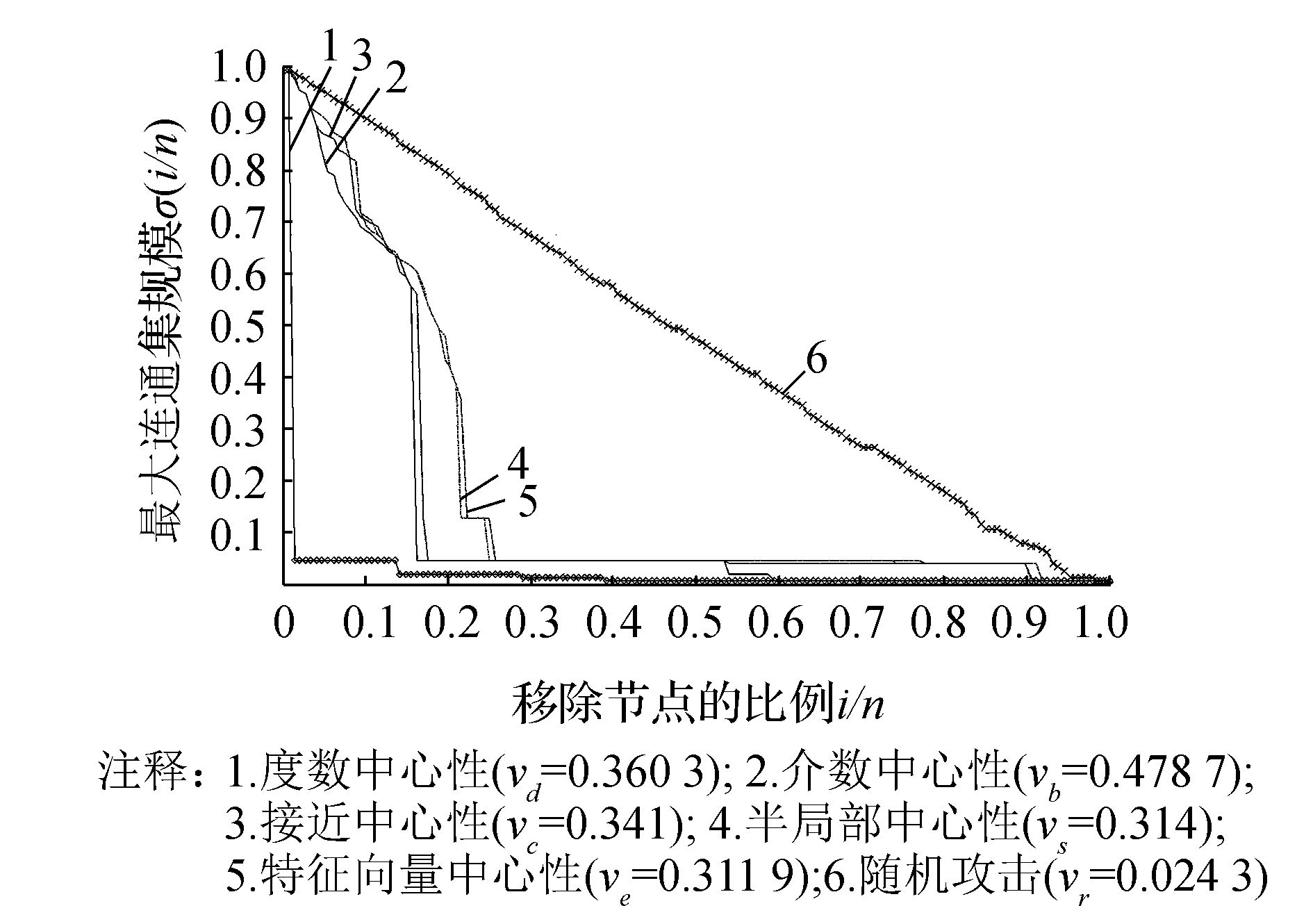
图 4为对中国航空网络模型分别进行随机攻击和蓄意攻击后,网络中移除节点的比例和最大连通集的规模之间的关系。在此需要说明的是,采用的攻击方式是同时移除i/n比例的节点,计算剩余网络中最大连通集所占的比例。
|
| 图 4 移除节点比例和最大连通集规模的关系(传统方法的攻击效果) Fig. 4 The relationship between the proportion of removed nodes and the scale of the largest connected component (Effect of traditional attack methods) |
从图 4可以看出,相比于蓄意攻击,随机攻击呈现的攻击效果较差,这表明中国航空网络对于随机攻击具有较好的鲁棒性。在蓄意攻击的仿真实验中,基于介数攻击下的指标下降率远远高于基于其他4种方法攻击下的指标下降率,而且下降速度很快,呈陡峭直线下降趋势。这表明针对中国航空网络,基于介数中心性的节点重要性排序方法效果是最好的,介数中心性能够更准确地刻画网络中节点的重要性。
基于各种攻击方法的中国航空网络脆弱性指标排序在表 2中给出,对比发现,蓄意攻击下的脆弱性指标远远高于随机攻击。在蓄意攻击中,介数中心性的指标Vb明显高于其他4种,排名第4的半局部中心性和排名第5的特征向量中心性在数值上比较接近。此外,从最大连通集的曲线图中也不难发现,半局部中心性和特征向量中心性的曲线是非常相近的。这就证明对于中国航空网络,半局部中心性和特征向量中心性的评价方法效果类似。
| 次序 | 攻击方法 | 脆弱性指标 |
| 1 | 介数中心性 | 0.479 |
| 2 | 度中心性 | 0.360 |
| 3 | 接近中心性 | 0.341 |
| 4 | 半局部中心性 | 0.314 |
| 5 | 特征向量中心性 | 0.312 |
| 6 | 随机攻击 | 0.024 |
另外,值得注意的是,当采用介数中心性对网络进行攻击的时候,曲线一开始就陡然下降,这一现象在其他攻击方法下并没有出现。单独观察介数攻击下网络的变化,发现在对北京进行攻击之后,网络的最大连通子图相对大小为0.993,而当对乌鲁木齐进行攻击之后,网络的最大连通子图相对大小骤然下降至0.047,网络几乎陷入瘫痪状态,这表明类似于乌鲁木齐这样的“桥”节点对于网络鲁棒性的影响举足轻重。
根据脆弱性指标判断,介数中心性能够更准确地描述节点的重要性,因此取基于介数中心性方法排列出的前20名节点城市,分别单独移除这些节点,用分析对网络造成的影响,具体数据见表 3。
| 次序 | 城市 | σ(i/n) | E | ΔE/E0 |
| 1 | 北京 | 0.993 | 0.479 | 0.047 |
| 2 | 乌鲁木齐 | 0.966 | 0.466 | 0.077 |
| 3 | 昆明 | 0.960 | 0.464 | 0.079 |
| 4 | 广州 | 0.987 | 0.483 | 0.037 |
| 5 | 上海 | 0.987 | 0.484 | 0.035 |
| 6 | 成都 | 0.980 | 0.480 | 0.045 |
| 7 | 西安 | 0.980 | 0.480 | 0.043 |
| 8 | 深圳 | 0.993 | 0.491 | 0.022 |
| 9 | 重庆 | 0.993 | 0.491 | 0.020 |
| 10 | 长沙 | 0.980 | 0.482 | 0.040 |
| 11 | 呼和浩特 | 0.993 | 0.493 | 0.017 |
| 12 | 贵阳 | 0.987 | 0.488 | 0.026 |
| 13 | 沈阳 | 0.993 | 0.493 | 0.018 |
| 14 | 哈尔滨 | 0.987 | 0.489 | 0.026 |
| 15 | 大连 | 0.993 | 0.493 | 0.018 |
| 16 | 杭州 | 0.993 | 0.492 | 0.019 |
| 17 | 合肥 | 0.987 | 0.488 | 0.026 |
| 18 | 长春 | 0.987 | 0.489 | 0.025 |
| 19 | 厦门 | 0.993 | 0.492 | 0.018 |
| 20 | 桂林 | 0.993 | 0.493 | 0.018 |
用σ(i/n)表示移除i/n比例的节点后最大连通子图的相对大小,E为网络的全局效率,E0为原始网络的全局效率,ΔE为网络减少的效率。结果表明,昆明机场的移除对网络的全局效率影响最大,其次是乌鲁木齐和北京。这也就进一步说明,昆明和乌鲁木齐在中国航空网络中的影响力不容小觑,从而验证了介数中心性指标的准确性。
这些城市在空间结构上基本上覆盖了中东部各地区,进一步观察局部地区的机场影响力情况,得到各个地区影响力最强的机场城市:华北地区——北京、华东地区——上海、华中地区——长沙、华南地区——广州、西北地区——乌鲁木齐、西南地区——昆明以及东北地区——哈尔滨。
4 簇度指标的提出在航空网络的背景下,介数中心性能够准确评价网络中节点的重要性,但其算法的时间复杂度较高,使其在实际应用中受到限制。
研究表明,除了节点邻居的直接影响力之外,邻居之间相互联系的紧密程度在节点的重要性评价中也起着至关重要的作用。Ugander等[19]对 Facebook 上一个用户收到某个邮件联系人的邀请信而成为 Facebook 用户情况进行了分析,发现影响节点重要性的决定性因素不是邻居节点的数目,而是邻居节点间形成的连通子图的数目。Centola[20]认为节点的传播影响力与节点的聚类系数有关,聚类系数越大越不利于信息的广泛传播。Chen等[21]在此基础上提出了一种针对有向网络的 ClusterRank算法,采用SIR传播模型进行仿真实验,结果表明该算法优于一些基准算法。任卓明等[4]将节点的二阶邻居度和聚类系数结合起来,提出了一种新的节点重要性评价方法,并分别用美国航空网络以及美国西部电力网验证了方法的有效性。
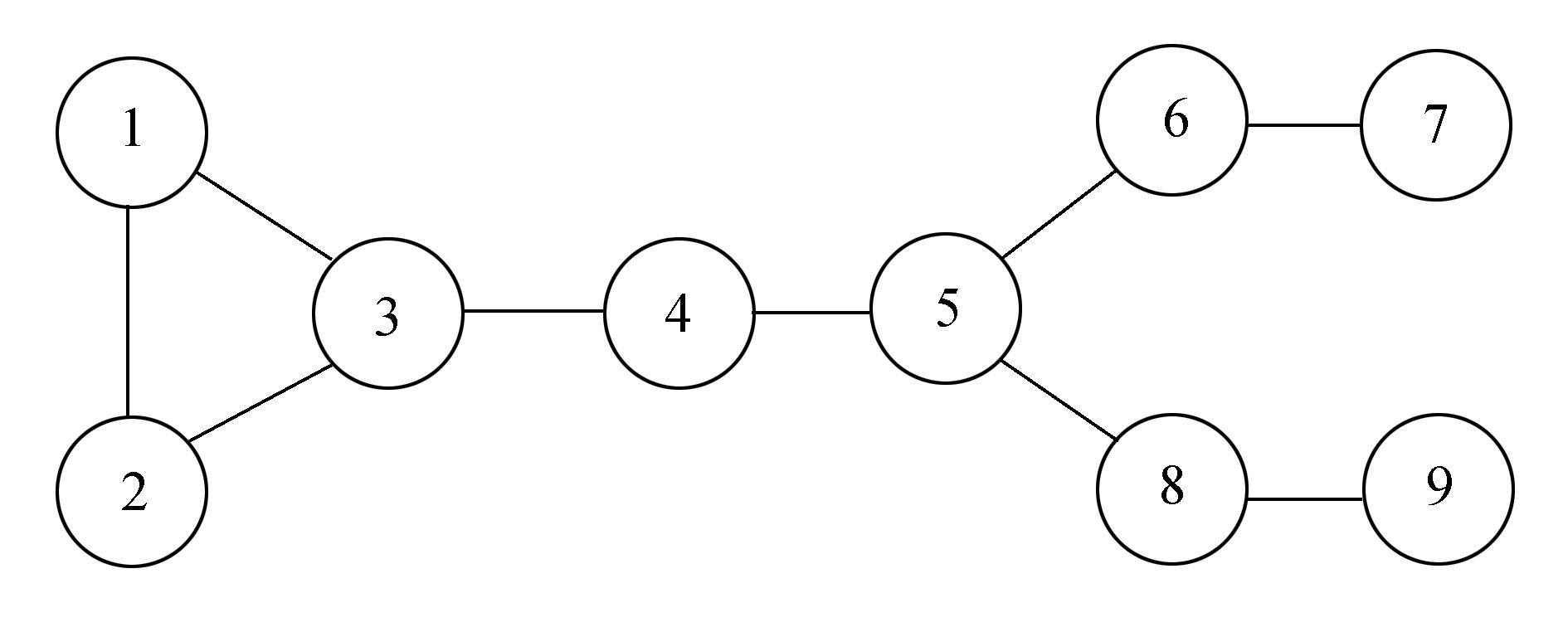
由此得出结论,局部聚类系数的增大对信息的传播是具有阻碍作用的,如果节点的邻居节点更倾向于互相连接,那么以节点为起始点,更容易形成一个局部的区域;相反,如果节点的邻居更倾向于连接除其邻居外的其他节点,那么信息才能够迅速在较大的范围内传播。例如在图 5中,节点3和节点5具有相同的度值ki以及相同的其邻居度之和,即 k3=k5=3,f3=f5=9,但是节点5的聚类系数比节点3更小(C3=0.33,C5=0),也就意味着节点5拥有比节点3更高的影响力。这是因为节点5的邻居节点更倾向于连接其他节点而不是互相连接,这样就能把信息传播到更广的范围内。
|
| 图 5 示例网络拓扑结构 Fig. 5 The topology of example network |
可见,节点的度和聚类系数对刻画其重要性都具有非常重要的意义。将节点的直接影响力和节点邻居之间连接的紧密程度结合起来,提出一种新的指标即簇度指标为:
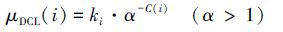 |
式中:ki为节点vi的度,α为可调参数,C(i)为节点i的聚类系数。
在此需要说明的是:
1) Chen和任卓明等在构造节点重要性指标中用到了二阶邻居度,但是由于航空网络的特殊性,即中转成本造成的平均路径长度较小,节点的直接影响力在评价节点重要性的过程中占主导地位。
2) 由于节点的聚类系数C(i)可能为0,故构造减函数α-C(i)(α>1),并通过仿真实验得到α的最优值,在后面的分析中我们将以中国航空网络为样本作出详细的描述。
5 实验分析为了验证簇度指标对节点重要性的度量效果,分别采用簇度指标以及上文提到的6种方法对中国航空网络进行蓄意攻击仿真实验,并用脆弱性指标来评价攻击效果。
经过调试得出,对于函数μ DCL(i),当α的取值范围为[4 724,4 952]时,脆弱性指标取最大值0.436,即得到的攻击效果最好。
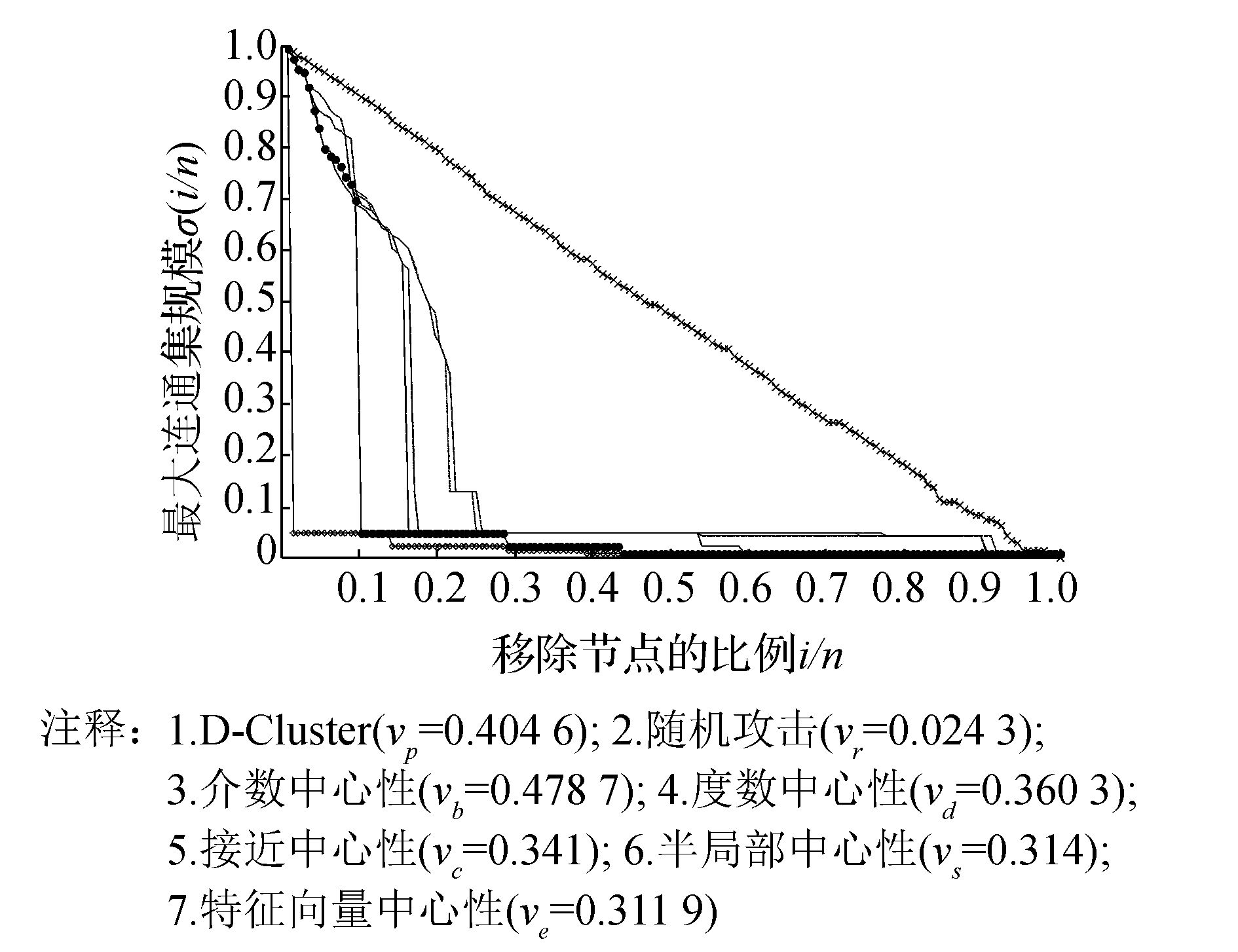
网络中移除节点的比例和最大连通集的规模之间的关系由图 6给出。从图 6中可以看出,按照簇度指标排列出的节点重要性顺序对中国航空网络进行蓄意攻击,得到的脆弱性指标数值为0.405,攻击效果仅次于介数中心性。但是介数的时间复杂度为O(N3);而该指标的时间复杂度为O(N),比介数中心性要快很多。例如在中国航空网络中,用介数排序需要0.03 s,而用簇度指标排序只需要0.01 s。
|
| 图 6 移除节点比例和最大连通集规模的关系(簇度指标与传统方法的攻击效果对比) Fig. 6 The relationship between the proportion of removed nodes and the scale of the largest connected component(Comparison of D-cluster index and traditional methods) |
本文分别用度中心性、接近中心性、介数中心性、特征向量中心性和半局部中心性5种方法对中国航空网络模型进行了分析,将网络中的节点按照重要性从大到小进行排序,并列出了重要性排名前10的节点城市;然后按排列出的节点次序对中国航空网络进行蓄意攻击,用脆弱性指标考察这5种方法的攻击效果。仿真结果表明,相比于其他4种方法,基于介数中心性的节点重要性排序方法能够更准确地刻画网络中节点的重要性。进而根据介数中心性得到的排序结果分别单独攻击各个城市节点,观察机场失效后网络的全局效率,分析得出各个局部地区的重要性节点。
此外,在航空网络的背景下,将节点的直接影响力和节点邻居之间连接的紧密程度结合起来,提出了一种基于度和聚类系数的新指标。对中国航空网络的仿真研究结果表明,该指标的评价准确性仅次于介数中心性,但是其时间复杂度比介数中心性低很多,具有很好的实用价值。
| [1] | 刘宏鲲, 周涛. 中国城市航空网络的实证研究与分析[J]. 物理学报 , 2007, 56 (1) : 106-112 LIU Hongkun, ZHOU Tao. Empirical study of Chinese city airline network[J]. Acta physica sinica , 2007, 56 (1) : 106-112 |
| [2] | 刘宏鲲. 中国航空网络的结构及其影响因素分析[D]. 成都:西南交通大学, 2007. LIU Hongkun. Analyzing the structure of Chinese aviation network and impact factors[D]. Chengdu:Southwest Jiaotong University, 2007. |
| [3] | 姚红光, 朱丽萍. 基于仿真分析的中国航空网络鲁棒性研究[J]. 武汉理工大学学报:交通科学与工程版 , 2012, 36 (1) : 42-46 YAO Hongguang, ZHU Liping. Research on robustness of China's aviation network based on simulation analysis[J]. Journal of Wuhan university of technology:transportation science & engineering , 2012, 36 (1) : 42-46 |
| [4] | 任卓明, 邵凤, 刘建国, 等. 基于度与集聚系数的网络节点重要性度量方法研究[J]. 物理学报 , 2013, 62 (12) : 128901 REN Zhuoming, SHAO Feng, LIU Jianguo, et al. Node importance measurement based on the degree and clustering coefficient information[J]. Acta physica sinica , 2013, 62 (12) : 128901 |
| [5] | 张珍, 张振宇, 宋蔓蔓. 一种基于最短路径介数的重要节点发现算法[J]. 计算机工程与应用 , 2013, 49 (21) : 98-100 ZHANG Zhen, ZHANG Zhenyu, SONG Manman. Important node searching algorithm based on shortest-path betweeness[J]. Computer engineering and applications , 2013, 49 (21) : 98-100 |
| [6] | BURT R S, MINOR M J. Applied Network Analysis[M]. Newbury Park, CA: Sage, 1983 : 195 -222. |
| [7] | 赫南, 李德毅, 淦文燕, 等. 复杂网络中重要性节点发掘综述[J]. 计算机科学 , 2007, 34 (12) : 1-5 HE Nan, LI Deyi, GAN Wenyan, et al. Mining vital nodes in complex networks[J]. Computer science , 2007, 34 (12) : 1-5 |
| [8] | BONACICH P. Factoring and weighting approaches to status scores and clique identification[J]. The journal of mathematical sociology , 1972, 2 (1) : 113-120 DOI:10.1080/0022250X.1972.9989806 |
| [9] | 汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012 . WANG Xiaofan, LI Xiang, CHEN Guanrong. Network science:an introduction[M]. Beijing: Higher Education Press, 2012 . |
| [10] | FREEMAN L C. Centrality in social networks conceptual clarification[J]. Social networks , 1978, 1 (3) : 215-239 DOI:10.1016/0378-8733(78)90021-7 |
| [11] | LATORA V, MARCHIORI M. Efficient behavior of small-world networks[J]. Physical review letters , 2001, 87 : 198701 DOI:10.1103/PhysRevLett.87.198701 |
| [12] | FREEMAN L C. A set of measures of centrality based upon betweenness[J]. Sociometry , 1977, 40 (1) : 35-41 DOI:10.2307/3033543 |
| [13] | CHEN Duanbing, LÜ Linyuan, SHANG Mingsheng, et al. Identifying influential nodes in complex networks[J]. Physica A , 2012, 391 (4) : 1777-1787 DOI:10.1016/j.physa.2011.09.017 |
| [14] | NEWMAN M E J. The structure and function of complex networks[J]. SIAM review , 2003, 45 (2) : 167-256 DOI:10.1137/S003614450342480 |
| [15] | 王姣娥, 莫辉辉, 金凤君. 中国航空网络空间结构的复杂性[J]. 地理学报 , 2009, 64 (8) : 899-910 WANG Jiao'e, MO Huihui, JIN Fengjun. Spatial structural characteristics of Chinese aviation network based on complex network theory[J]. Acta geographica sinica , 2009, 64 (8) : 899-910 |
| [16] | LATORA V, MARCHIORI M. Efficient behavior of small-world networks[J]. Physical review letters , 2001, 87 (19) : 198701 DOI:10.1103/PhysRevLett.87.198701 |
| [17] | SCHNEIDER C M, MOREIRA A A, ANDRADE JR J S, et al. Mitigation of malicious attacks on networks[J]. Proceedings of the national academy of sciences of the United States of America , 2011, 108 (10) : 3838-3841 DOI:10.1073/pnas.1009440108 |
| [18] | IYER S, KILLINGBACK T, SUNDARAM B, et al. Attack robustness and centrality of complex networks[J]. PLoS one , 2013, 8 (4) : e59613 DOI:10.1371/journal.pone.0059613 |
| [19] | UGANDER J, BACKSTROM L, MARLOW C, et al. Structural diversity in social contagion[J]. Proceedings of the national academy of sciences of the United States of America , 2012, 109 (16) : 5962-5966 DOI:10.1073/pnas.1116502109 |
| [20] | CENTOLA D. The spread of behavior in an online social network experiment[J]. Science , 2010, 329 (5996) : 1194-1197 DOI:10.1126/science.1185231 |
| [21] | CHEN Duanbing, GAO Hui, LÜ Linyuan, et al. Identifying influential nodes in large-scale directed networks:the role of clustering[J]. PLoS one , 2013, 8 (10) : e77455 DOI:10.1371/journal.pone.0077455 |



