近些年,随着计算机网络系统、无人机、卫星系统的高速发展,关于多智能体系统的研究也成为人们研究的热点。由于多智能体系统间各智能体的协调控制能实现我们所需要的复杂运动,因此有关多智能体系统的研究具有十分重要的意义。在研究多智能体系统时,我们利用代数图论[1]的知识,把多智能体系统用拓扑图表示。其中,拓扑图的节点代表各智能体,拓扑图的边代表各智能体间的连接关系。在研究过程中,产生了两个重大的结果,能控性和一致性。多智能系统的能控性首先是由Tanner[2]提出来的,通过利用经典能控性概念,把拉普拉斯矩阵分块为子矩阵,得到能控性判据。近年来,多智能体系统的能控性研究受到国内外科研工作者的广泛关注[3-8]。然而,在能控性保持方面的研究工作则刚刚起步,目前主要是以L.Sabattini[9-12]的研究为主。
一致性问题的研究可以追溯到20世纪70年代的管理科学和统计领域[13-14]。目前关于一致性问题的研究很大程度上以T.Vicsek[15]提出的Vicsek模型为基础。多智能体系统的一致性主要是研究如何基于多智能体系统中个体之间有限的信息交换,实现所有智能体的某个或某些状态量趋于相等的问题。对一致性协议的研究能让我们清楚地了解到智能体之间信息交换的过程。Olfati-Saber[16]提出了解决多智能体网络系统的一致性协议的理论框架, 并且得到在连续时间一阶多智能体系统中,当通信拓扑结构表示的图为无向图时,多智能体系统的一致速度取决于图的拉普拉斯矩阵的第二小特征值的结论,即一致性速度与拓扑图的拉普拉斯矩阵第二小特征值λ2之间存在正相关的关系。同时在文献[1, 16-18]中,对第二小特征值λ2的物理意义也做出了说明,并指出了λ2不仅可以度量一致性速度,也可以表示智能体系统的稳定性。
在一致性问题中,以一阶邻居协议的研究最为普遍,即考虑智能体的邻居信息。一阶邻居协议具有适用面广泛、作用原理简单的优点。然而由于多智能体系统越来越复杂,一阶邻居协议的信息交换方式已经不能满足我们的需要,例如在复杂的全球卫星网络 (GPS) 中,采用一阶邻居协议显然会使信息的交换效率低下,整个卫星系统协同控制效果并不好。而采用二阶邻居协议,由于系统收敛性比前者更好,这就为复杂卫星网络系统的运转提供更高效的保障。因此,对二阶邻居协议的研究就显得尤为重要。和一阶邻居协议相比,二阶邻居协议不仅利用智能体邻居的信息,还利用其二阶邻居的信息,而系统实际的通信拓扑结构并未发生变化。本文通过对上述两种一致性协议进行比较,得出了多智能体系统采用二阶邻居协议时,多智能体系统中各智能体达到一致性速度更快的结论。同时,针对现实中具有时变拓扑结构的系统,为了使网络系统能够更稳定运转,避免受外部环境的影响,以达到人们需要的工作状态,这就对系统的能控性和能观测性提出了很大要求,就需要领航者对跟随者的控制能力一直保持下去。本文通过借助结构能控性的概念和性质[19-20],设计了一种全新的控制策略,使多智能体系统的能控性和能观测性得到保持。这对于易受外界环境干扰的多智能体系统的研究具有较高的理论价值。
1 预备知识在这篇文章中,我们所研究的拓扑图都是初始状态连通的无向图。无向图可以用G=(V, E, A) 表示,其中,集合V表示图的节点集,集合E表示连接节点的边集,E={e1, e2, …, ej},矩阵A=[aij]为图G的邻接矩阵,其中元素aij为节点vi与vj之间的边的权重。令矩阵D=[dij]为图G的度矩阵, 且当i=j时,元素dij表示为节点vi的度数;当i≠j时,dij=0。
拉普拉斯矩阵是表示拓扑图节点与边关系的一种矩阵, 也是我们研究多智能体系统需要借助的一个重要概念。对于一个包含N个节点的无向图G, 其拉普拉斯矩阵定义为L=D-A,拉普拉斯矩阵还可以表示为L=ITI,其中矩阵I=[iij]表示把无向图G规定为具有任意方向有向图的关联矩阵,元素
 |
拉普拉斯矩阵具有如下性质:
1) 对于一个所有元素均为1的列向量,L与该列向量的乘积为零矩阵;
2) 令λ1, λ2, …, λN为拉普拉斯矩阵的特征值,则0=λ1≤λ2≤…≤λN;
3) 第1个非零特征值 (第2个最小的特征值λ2) 称为代数连通度。
文中对二阶邻居协议下的多智能体系统进行了讨论。因此,我们需要掌握合并图的概念。合并图是由节点与实际边组成的实际图g和节点与虚拟边组成的虚拟图gv构成。因此,合并图的拉普拉斯矩阵Lc分别由图G中实际图的拉普拉斯矩阵L和虚拟图的拉普拉斯矩阵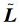
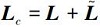

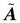


考虑具有N个智能体的多智能体系统,并且此系统可以用无向图G=(V, E, A) 表示。记xi为第i个智能体的状态,每个智能体的状态遵循如下一阶动力学方程:
 |
(1) |
式中xi(t) 和ui(t) 分别为智能体i的状态和输入。
设Ni为智能体i的邻居集,即Ni={j∈V(G)|(vi, vj)∈E(G)}。那么在一阶邻居协议下,
 |
(2) |
设Ni2为智能体i的二阶邻居集,即Ni2={k∈v|k∈Nj, j∈Ni, k≠i, k∉Ni }。所以各智能体之间通过二阶邻居一致性协议进行下式连接:
 |
(3) |
式中:wij为实际图中节点之间的权值,wik为虚拟图节点之间权值。
在式 (3) 中,每个智能体在获取自己的状态信息时不仅利用其邻居的状态信息,还利用其二阶邻居的状态信息。由于智能体i与其二阶邻居之间并不存在实际的通信链路,所以智能体i的二阶邻居的信息由智能体i的邻居间接传递给i。由式 (1) 和式 (3),系统中每个智能体的状态可以表示为
 |
(4) |
令wij=wik=1,则
 |
所以系统可以写为如下这种形式:
 |
(5) |
引理1[16] 拉普拉斯矩阵Lc的第二小特征值λ2可用于表征系统一致收敛的速度。
证明 构造一个李雅普诺夫函数:
 |
对此函数求导可得
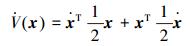 |
结合式 (5) 得
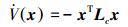 |
因为图G是无向连通图,所以[16]:
 |
即λ2(G)‖x‖2≤xTLx,故
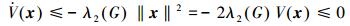 |
所以x的状态与λ2相关,当
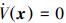
证毕。
定理1 对于一阶多智能体系统 (1),它在二阶邻居协议 (3) 下达到一致性的速度比在一阶邻居协议 (2) 下更快。
证明对于一个具有N个节点的无向图G,假设在一阶邻居协议 (2) 下它的拉普拉斯矩阵为L,关联矩阵为I,那么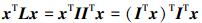


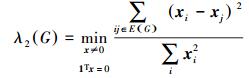 |
(6) |
在二阶邻居协议 (3) 下,节点xi不仅考虑与它邻居节点xj间的连接关系,还需要考虑与二阶邻居节点xk之间的连接关系。因此,如果ik∈E(gv) 时,其中
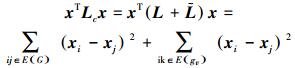 |
因此
 |
(7) |
显然,式 (7) 大于式 (6),即多智能体系统在二阶邻居协议下达到一致性的速度比在一阶邻居协议下更快。证毕。
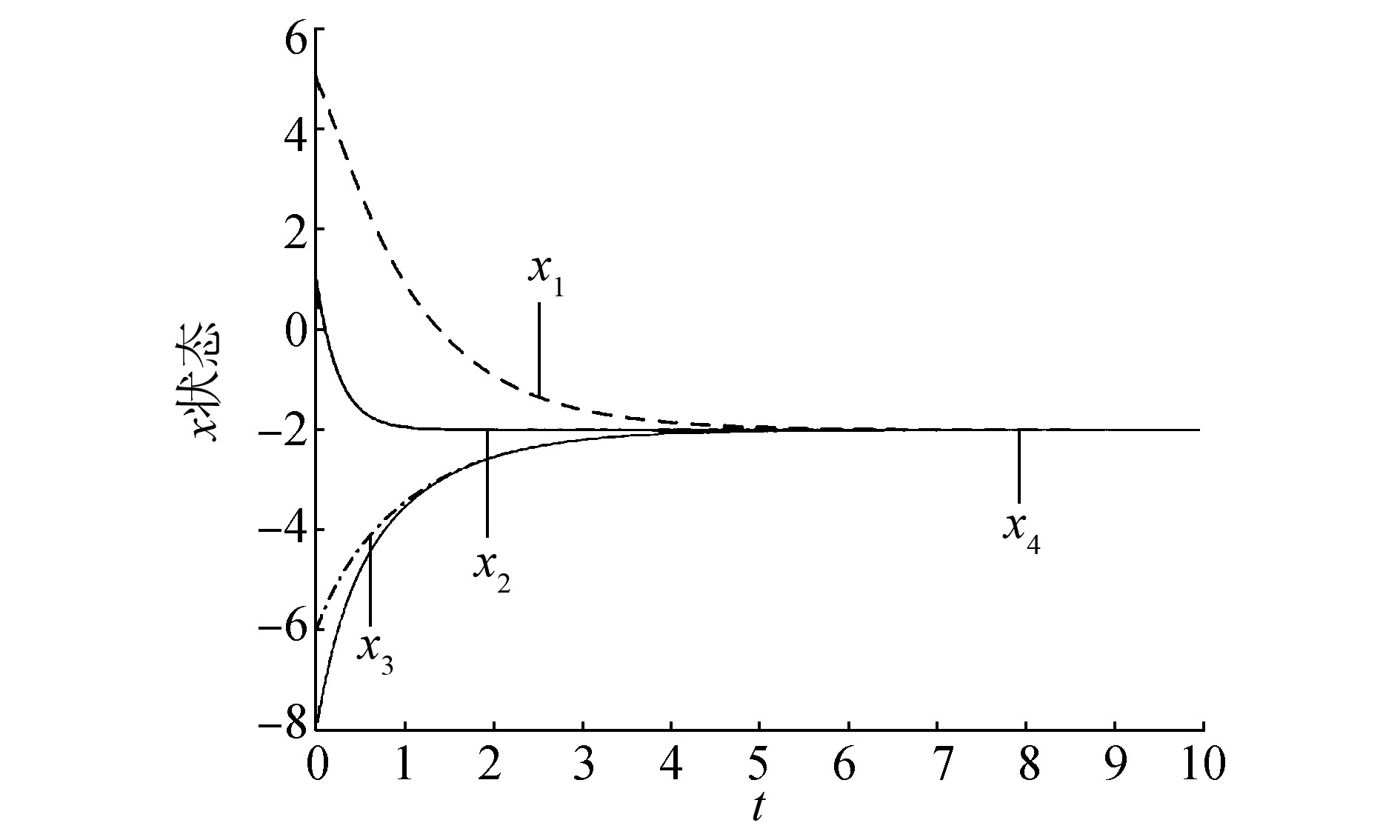
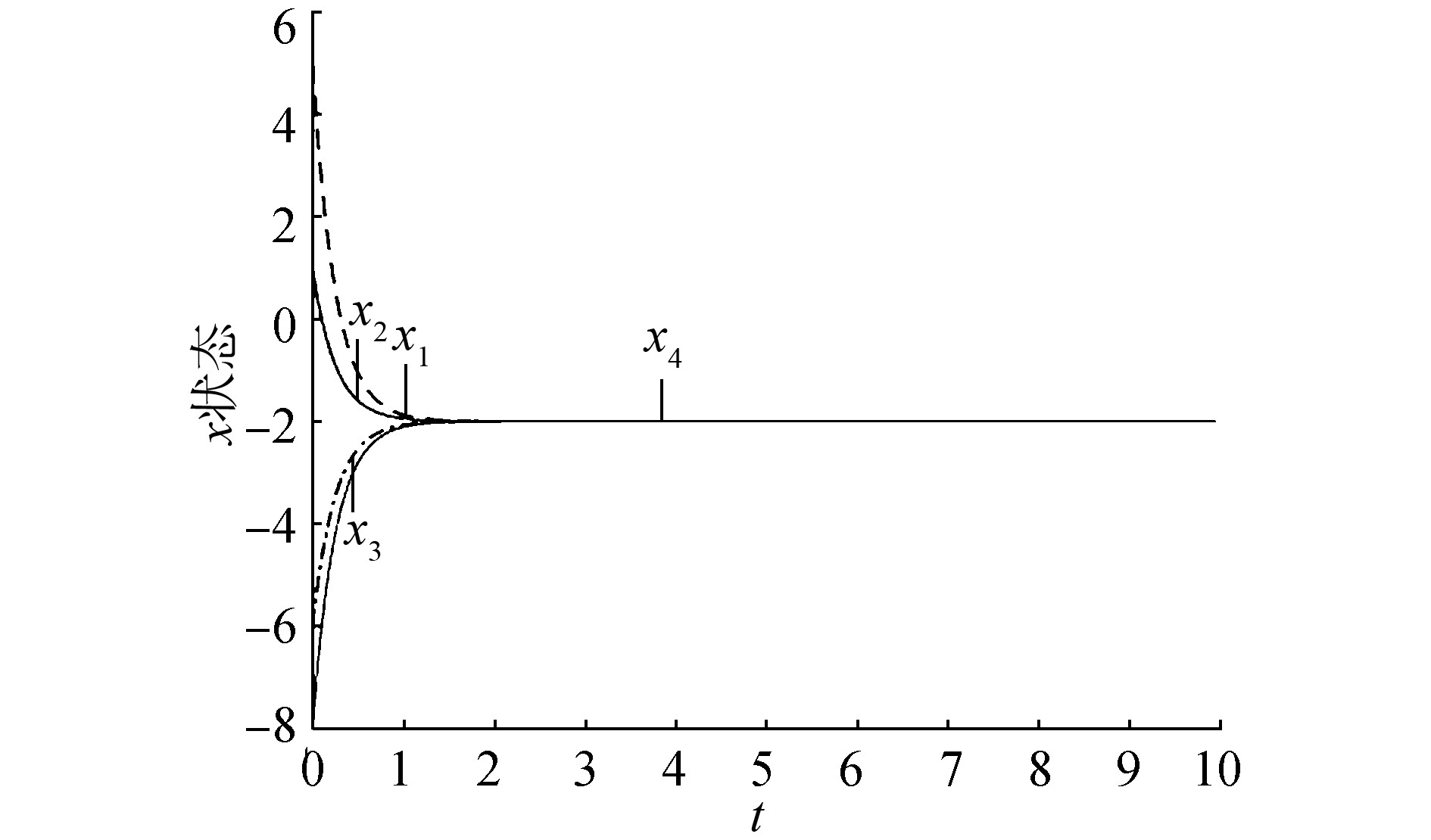
我们也可以借助例子对定理1做进一步理解。对于具有4个节点的多智能体系统 (1),假设各智能体在t=0时刻的状态分别为x(0)=[5 1 -6 -8]T。通过借助MATLAB可以分别绘制出系统在一阶邻居协议 (2) 下各个智能体的状态轨迹 (图 1) 和系统在二阶邻居协议 (3) 下各个智能体的状态轨迹 (图 2)。
|
| 图 1 一阶邻居协议下各智能体的状态轨迹 Fig. 1 The state trajectory of each agent under the first-order neighbors protocol |
|
| 图 2 二阶邻居协议下各智能体的状态轨迹 Fig. 2 The state trajectory of each agent under the second-order neighbors protocol |
通过对图 1和图 2进行比较分析,我们发现多智能体系统 (1) 在二阶邻居协议 (3) 下的收敛性更好,即在二阶邻居协议 (3) 下各智能体达到一致性的速度要比在一阶邻居协议 (2) 下更快。因此,在设计多智能体系统时,尽可能地选用基于二阶邻居的一致性协议,会使系统更快速地达到一致性。
为了控制多智能体系统 (1) 的状态,我们把能够获得外部控制输入的智能体称为领航者,其余的智能体称为跟随者。令VL(G) 为领航者的集合,VF(G)=V(G)-VL(G) 为跟随者的集合, 则基于二阶邻居的一致性协议 (3) 规则可以修改为
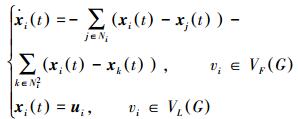 |
(8) |
式中:ui=ui(t)∈R为外部控制输入,且u及
 |
(9) |
当在系统中选取后几个节点为领航者时,我们把前NF(NF≥1) 个节点记为跟随者的个数,其余的节点代表领航者的个数, 记为NL(NL≥1)。所以在具有N个智能体的系统中,NF=N-NL。根据文献[21],合并图的拉普拉斯矩阵Lc可分块为
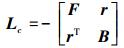 |
式中:矩阵F∈RNF×NF代表跟随者之间的传递关系,矩阵B∈RNL×NL代表领航者之间的传递关系,矩阵r∈RNF×NL代表领航者和跟随者之间的传递关系。
当在系统中选取任意多个节点为领航者时,假设系统中有NL个领航者,我们规定矩阵r取自矩阵Lc中这NL个节点所在的列向量减去这NL个节点所在行向量和列向量的共同元素后剩余元素所组成的NF×NL矩阵。矩阵-F为合并图拉普拉斯矩阵Lc减去这NL个节点所在行和所在列后剩下的NF×NF矩阵。
3 实例分析对于一个具有5个节点的拓扑图,我们取第2个和第4个节点作为领航者,如图 3。

|
| 图 3 具有5个节点的拓扑图 Fig. 3 Topology with 5 nodes |
那么
 |
所以
 |
假设领航者能够获得输出向量y,且y∈RNL×1,那么,网络系统的动态方程可以写为文献[9]所描述的那样:
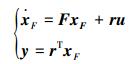 |
(10) |
定理2 若合并图的拉普拉斯矩阵Lc的子矩阵F所对应的正交特征向量组成的矩阵U不与向量r正交,则此拓扑图所对应的多智能体系统既是能控的,又是能观测的。
证明 根据式 (10),可得能控性判别矩阵:
 |
(11) |
因为拉普拉斯矩阵L与


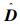
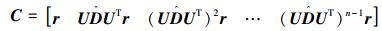 |
可写为
 |
因为U是非奇异矩阵,若使能控性判别矩阵C满秩,只需要保证矩阵
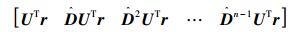 |
行满秩即可。又因为对角矩阵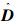
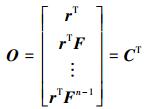 |
(12) |
同理,若使能观性判别矩阵O满秩, 则也需使UTr≠0。也就是说,若多智能体系统是能控的,那么它也是能观测的。证毕。
综上所述,在二阶邻居协议下,多智能体系统既能控又能观测的条件为:矩阵F所对应的特征向量U不与向量r正交。
4 对结构能控性维持策略的研究在基于二阶邻居协议 (3) 下具有时变拓扑结构的多智能体系统 (1) 随时间变化过程中,各节点之间边的条数和距离可能发生变化,进而影响系统合并图的拉普拉斯矩阵Lc,并根据定理2和文献[1],在某一时刻,可能也会导致代数连通度λ2发生改变以及使得系统不能控。因此,为了避免具有时变拓扑结构的多智能体系统 (1) 的能控性发生改变,我们引入了结构能控性的概念。
4.1 结构能控性定义1 对于一个无权重的多智能体系统,如果能够找到至少一组权重,使得相应的系统变为能控,那么称这个多智能体系统是结构能控的。
在文章[18]中,可以知道多智能体系统是结构能控的,当且仅当系统的拓扑图是连通的,即代数连通度λ2>0。可以借助结构能控性的概念,通过给拓扑图的边赋予相应的权值,使本来不能控的系统变为能控,以达到对多智能体系统的状态要求。
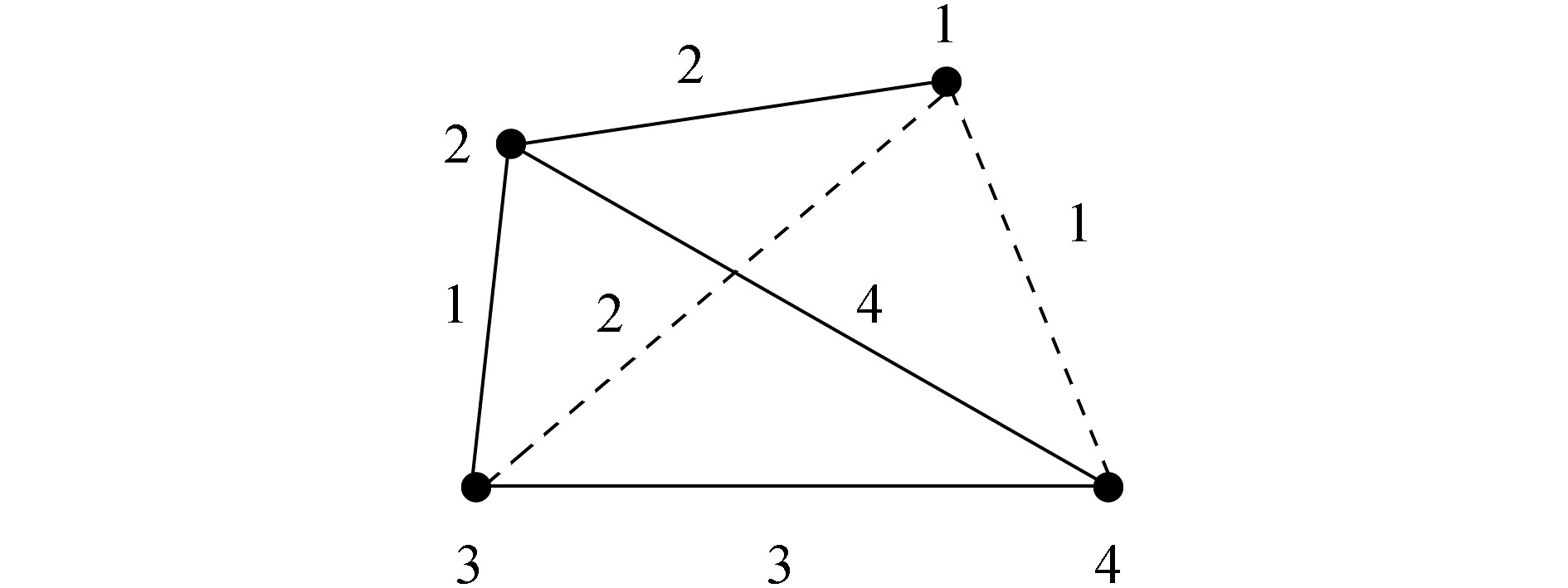
4.2 实例分析对于图 4所示的简单图G,我们给边赋予一组权值,其中,实线表示实际图g的连结方式,虚线表示虚拟图gv的连结方式,我们选择第4个节点作为领航者,那么:实际图的拉普拉斯矩阵L和虚拟图的拉普拉斯矩阵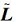
|
| 图 4 权图 Fig. 4 Weight graph |
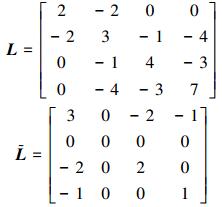 |
所以基于二阶邻居协议下多智能体系统的拉普拉斯矩阵为
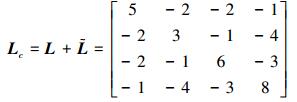 |
由式 (11) 得,能控性判别矩阵为
 |
式中:rank (C)=3。所以,通过给边赋予权值后,网络系统具有能控性和能观测性。因此我们就称原系统是结构能控的。
根据结构能控性的定义和文献[18],可得到图 5所示的多智能体系统能控性和结构能控性的关系:

|
| 图 5 多智能体系统能控性和结构能控性的关系 Fig. 5 Relationship between controllability and structural controllability of multi-agent system |
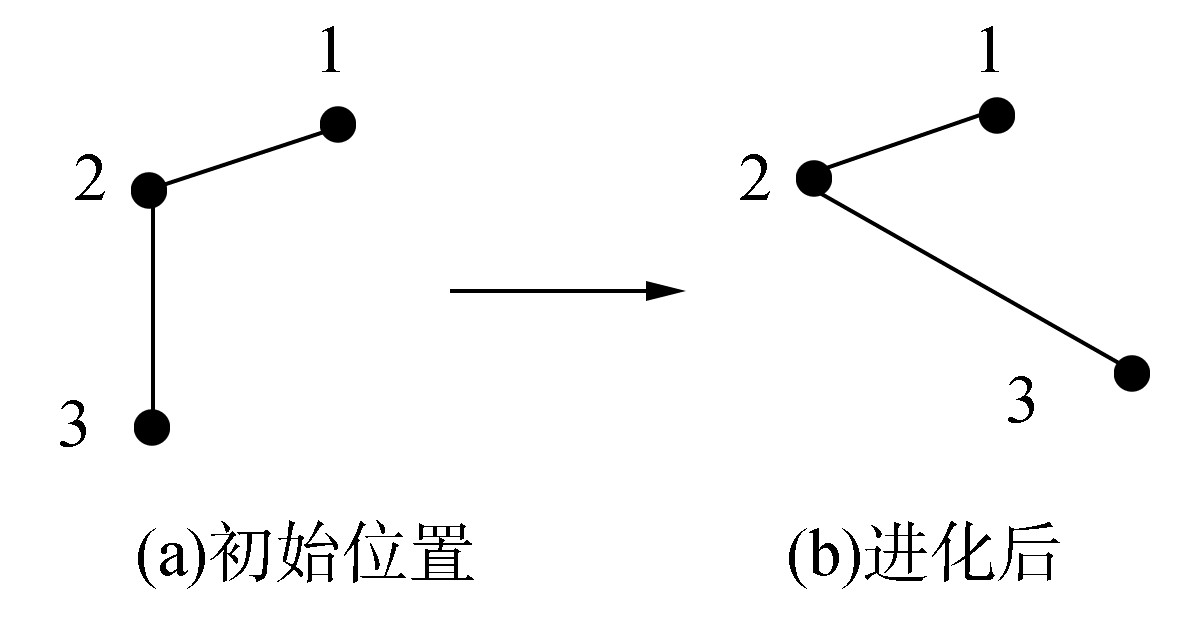
在本文中,具有时变拓扑结构的多智能体系统 (1),随着时间的变化,可能会导致已连通的节点之间的距离增加,从而使连通强度改变,导致系统的能控性发生变化。我们的目的只考虑如何使已连通节点间的连通强度不随时间消失,而关于不连通的节点是否会随时间而靠近从而连通的情况则不进行相关分析。如图 6所示,其中 (a) 为网络系统的初始位置,设点1为领航者,并给它注入某一控制输入,则各智能体在到达一致状态的过程中,显然由 (b) 可看出,由于第2点和第3点的距离变大,致使两点的连接强度减弱,这显然不符合多智能体系统的设计要求。
|
| 图 6 时变拓扑结构 Fig. 6 Time varying topology |
因此,为了避免上述情况的出现,在本章节提出了一个控制策略,如式 (13) 所示:
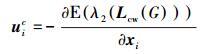 |
(13) |
式中:Lcw(G) 为合并图的权拉普拉斯矩阵,实际图g的权值与智能体xi、xj之间的距离成反比,即随着智能体间距离的增加,权值减小。为了易于理解,我们给wij赋予通信联系强弱的物理意义。我们可以用式 (14) 来描述权值与智能体距离之间的关系。设R为任意两个智能体间的最大通信距离,即
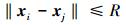 |
时,两个智能体间有通信联系,节点xi、xj之间存在边eij,此时wij>0。那么
 |
(14) |
式中:κ满足e-R2/κ2=ω,ω是一个比0大的常数。当wij=0时,说明智能体xi、xj之间没有通信联系,即不存在边eij。同理,虚拟图gv的权值:
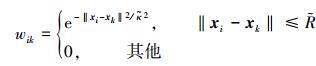 |
(15) |
式中:

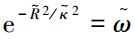

由文献[1]可以知道,在权图中,λ2与权值wij有关,即随着wij减小,对应着λ2的值也将减小。但当wij=0时,由于一条边的减少不一定会导致拓扑图的连通性发生改变,因此λ2不一定为零。而当所有边的权值都为零,即智能体间都没有通信关系时,拓扑图必定不连通,此时λ2=0。
函数Ε(λ2(·)) 为能量函数,当且满足以下性质:
1) ∀λ2(·)>0,能量函数连续可微;
2) 能量函数是非负的。
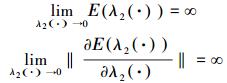 |
因此,可以写出能量函数的表达式为
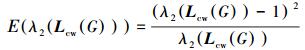 |
(16) |
所以网络系统的动态方程可以修改为式 (7) 形式:
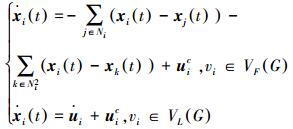 |
(17) |
定理3 考虑上述基于二阶邻居一致性协议 (3) 下的动态系统 (1),令系统在t=0时刻是结构能控的,那么,控制策略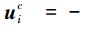

证明 在t=0时刻,假设多智能体系统 (1) 结构能控,即拓扑图连通,此时λ2>0。式 (17) 所描述的动态方程可以修改为如下形式:
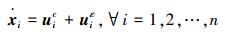 |
(18) |
式中:外部输入uiε是有界的,即∃uM∈R,使得
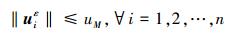 |
(19) |
能量函数对时间的导数可以写为以下形式:
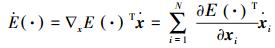 |
由式 (13) 和式 (18) 可得,能量函数的导数也可写为
 |
根据式 (19),并由
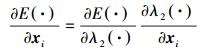 |
可得下列不等式:
 |
因此,如果不等式
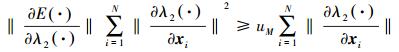 |
(20) |
成立,则
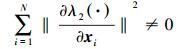 |
(21) |
那么,式 (20) 所描述的不等式就可以写为
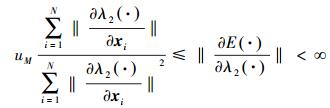 |
(22) |
根据能量函数的性质,∃λ>0,使得λ2(·)≤λ,不等式 (22) 成立。这也表明λ2(·) 的值大于零。假设
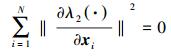 |
(23) |
式 (23) 成立,那么
因此由上述结论可知:如果在初始时刻拓扑图连通,那么随着时间的变化,即使拓扑图的结构发生变化,其所对应的拉普拉斯矩阵的第2个特征值λ2也会永远大于零。那么多智能体系统的结构能控性得到了保持。证毕。
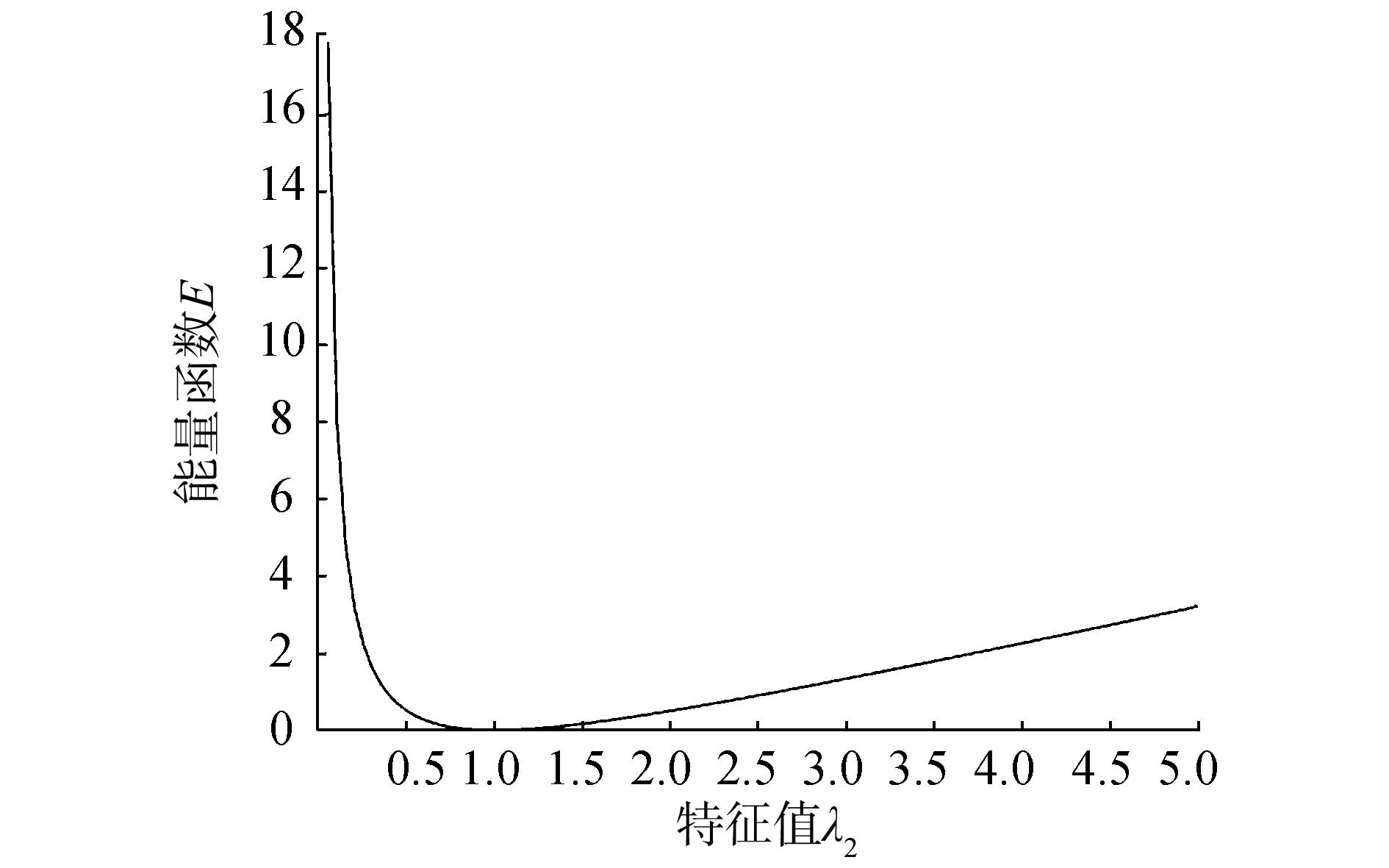
根据能量函数的图像可以进一步理解上述结论。能量函数的图像如图 7所示。
|
| 图 7 能量函数Ε的图像 Fig. 7 Image of energy function E |
由能量函数的图像可知,如果在初始时刻给具有结构能控性的系统赋予一组权重不为1的权值,那么不仅说明λ2恒大于零,系统结构能控性得到保持,还说明拓扑图恒连通,任意节点都会与其他至少一个节点相连接。即‖xi-xj‖≤R,存在权值wij。又因为权值wij=1时,由式 (14) 和式 (15) 得,‖xi-xj‖=0,显然无意义。因此权值wij≠1,所以结构能控性得到保持的系统必定存在一组边的权值,且权值不为1。因此多智能体系统 (1) 具有能控性和能观测性。
综上,通过在初始时刻赋予多智能体系统一组权值且引入控制策略uic,具有时变拓扑结构的多智能体系统的能控性和能观测性得到保持。
4 结束语由于二阶邻居协议式 (3) 在到达一致性的速度上比一阶邻居协议式 (2) 更有优势,所以本文对二阶邻居协议式 (3) 下的多智能体方面进行了研究,并对相关定理通过算例进行验证。而对于智能体与二阶邻居通信过程中可能会出现时滞的情况,这将是未来的一个重点研究的问题。本文对具有时变拓扑结构的多智能体系统的一致性协议的选取和能控性保持方面的研究提供了一个方向和基础。
| [1] | GODSIL C, ROYLE G. Algebraic graph theory[M]. New York: Springer, 2001. |
| [2] | TANNER H G. On the controllability of nearest neighbor interconnections[C]//Proceedings of the 43rd IEEE Conference on decision and Control. Nassau, 2004, 3: 2467-2472. |
| [3] | JI Zhijian, LIN Hai, YU Haisheng. Protocols design and uncontrollable topologies construction for multi-agent networks[J]. IEEE transactions on automatic control, 2015, 60(3): 781-786. DOI:10.1109/TAC.2014.2335971. |
| [4] | JI Zhijian, LIN Hai, YU Haisheng. Leaders in multi-agent controllability under consensus algorithm and tree topology[J]. Systems & control letters, 2012, 61(9): 918-925. |
| [5] | JI Zhijian, WANG Zidong, LIN Hai, et al. Interconnection topologies for multi-agent coordination under leader-follower framework[J]. Automatica, 2009, 45(12): 2857-2863. DOI:10.1016/j.automatica.2009.09.002. |
| [6] |
晁永翠, 纪志坚, 王耀威, 等. 复杂网络在路形拓扑结构下可控的充要条件[J].
智能系统学报, 2015, 10(4): 577-582.
CHAO Yongcui, JI Zhijian, WANG Yaowei, et al. Necessary and sufficient conditions for the controllability of complex networks with path topology[J]. CAAI transactions on intelligent systems, 2015, 10(4): 577-582. |
| [7] |
董洁, 纪志坚, 王晓晓. 多智能体网络系统的能控性代数条件[J].
智能系统学报, 2015, 10(5): 747-754.
DONG Jie, JI Zhijian, WANG Xiaoxiao. Algebraic conditions for the controllability of multi-agent systems[J]. CAAI transactions on intelligent systems, 2015, 10(5): 747-754. |
| [8] |
王晓晓, 纪志坚. 广播信号下非一致多智能体系统的能控性[J].
智能系统学报, 2014, 9(4): 401-406.
WANG Xiaoxiao, JI Zhijian. Controllability of non-identical multi-agent systems under a broadcasting control signal[J]. CAAI transactions on intelligent systems, 2014, 9(4): 401-406. |
| [9] | SABATTINI L, SECCHI C, FANTUZZI C. Controllability and observability preservation for networked systems with time varying topologies[C]//Proceedings of the 19th World Congress on the International Federation of Automatic Control. Cape Town, South Africa, 2004: 1837-1842. |
| [10] | SABATTINI L, CHOPRA N, SECCHI C. On decentralized connectivity maintenance for mobile robotic systems[C]//Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, USA, 2011: 988-993. |
| [11] | SABATTINI L, CHOPRA N, SECCHI C. Distributed control of multi-robot systems with global connectivity maintenance[C]//Proceedings of 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Francisco, CA, 2011: 2321-2326. |
| [12] | SABATTINI L, SECCHI C, COCETTI M, et al. Implementation of coordinated complex dynamic behaviors in multirobot systems[J]. IEEE transactions on robotics, 2015, 31(4): 1018-1032. DOI:10.1109/TRO.2015.2452774. |
| [13] | DEGROOT M H. Reaching a Consensus[J]. Journal of the American statistical association, 1974, 69(345): 118-121. DOI:10.1080/01621459.1974.10480137. |
| [14] | CHATTERJEE S, SENETA E. Towards consensus: some convergence theorems on repeated averaging[J]. Journal of applied probability, 1977, 14(1): 89-97. DOI:10.1017/S0021900200104681. |
| [15] | VICSEK T, CZIRóK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical review letters, 1995, 75(6): 1226-1229. DOI:10.1103/PhysRevLett.75.1226. |
| [16] | OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE transactions on automatic control, 2004, 49(9): 1520-1533. DOI:10.1109/TAC.2004.834113. |
| [17] | REN Wei, BEARD R W, MCLAIN T W. Coordination variables and consensus building in multiple vehicle systems[M]//KUMAR V, LEONARD N, MORSE A S. Cooperative Control. Berlin Heidelberg: Springer, 2005: 171-188. |
| [18] | FIEDLER M. Algebraic connectivity of graphs[J]. Czechoslovak mathematical journal, 1973, 23(2): 298-305. . |
| [19] | ZAMANI M, LIN Hai. Structural controllability of multi-agent systems[C]//Proceedings of 2009 American Control Conference. St. Louis, USA, 2009: 5743-5748. |
| [20] | LIN C T. Structural controllability[J]. IEEE transactions on automatic control, 1974, 19(3): 201-208. DOI:10.1109/TAC.1974.1100557. |
| [21] | EGERSTEDT M, MARTINI S, CAO Ming, et al. Interacting with networks: how does structure relate to controllability in single-leader, consensus networks[J]. IEEE control systems, 2012, 32(4): 66-73. DOI:10.1109/MCS.2012.2195411. |



