2. 广西师范大学 广西多源信息挖掘与安全重点实验室, 广西 桂林 541004
2. Guangxi Key Lab of Multi-source Information Mining & Security, Guilin 541004, China
近几年来,子空间聚类[1]方法作为一种实现高维数据聚类的有效途径,在机器学习、图像处理和计算机视觉等领域已得到广泛应用。其中基于稀疏表示(sparse representation)和低秩表示(low-rank representation)的子空间聚类方法,通过与图划分的谱聚类方法相结合,在运动图像分割、人脸识别等高维数据的聚类方面得到了较好的效果。
子空间聚类又称子空间分割是指把数据的原始特征空间分割为不同的特征子集,从不同的子空间角度考察各个样本聚类划分的意义,同时在聚类过程中为每个样本寻找相应的特征子空间。目前实现子空间聚类的方法主要归为以下4类:基于代数的,如GPCA算法[2];基于迭代的,如K-subspaces[3];基于统计的,如PCA和RANSAC算法[4];以及基于谱聚类的,如SSC(sparse subspace clustering)[5],LRR(low-rank representation)[6]和LSR(least squares regression)[7]算法等。其中,基于谱聚类的子空间聚类算法利用样本的局部或全局信息去构建一个相似度矩阵,然后通过谱聚类算法对样本进行聚类。该类方法能较好地处理具有噪音和离群点的数据,不需要事先知道子空间的个数以及维数,因此在手写体识别、人脸识别以及运动分割等多个应用领域获得非常好的效果。
目前比较流行的算法有基于谱聚类的SSC和LRR算法,它们主要是对每个样本都找到一组稀疏或低秩的线性表示去构建相似度矩阵,然后利用谱聚类得到最终的结果。其中,SSC算法能够很好地结合样本自表达和稀疏相似度矩阵,通过稀疏相似度矩阵可使每个样本由与其相似性很强的一些样本表示,这些具有强相似性的样本往往在同一个子空间里,所以具有一定稀疏性的相似度矩阵往往可以提高子空间聚类的效果。但是,在数据的信噪比小、子空间不相互独立的情况时,该方法的聚类效果就不是很好。而LRR算法可以很好地使样本自表达和去除噪音、离群点相结合,但是其通过低秩表示构造的相似度矩阵往往不稀疏,没有很好地利用样本间的强相关性,这会影响子空间聚类的效果。
因此,合理地结合利用样本自表达和稀疏相似度矩阵以及去除噪音、离群点的干扰,能够实现构造一个良好的相似度矩阵而获得更好的子空间聚类效果的目的。所以,本文提出的方法首先从样本之间的相关性出发,对所有测试样本进行样本自表达,并同时通过L1-norm和L2, 1-norm正则化项惩罚相似度矩阵,进行稀疏约束得到全局最优的相似度矩阵。然后,利用谱聚类得到最终的子空间聚类结果。在样本自表达过程中,L1-norm正则化项用来实现相似度矩阵的稀疏,确保每个测试样本都由与之相关性强的样本表示,能很好地解决样本自表达和稀疏相似度矩阵相结合的问题;而L2, 1-norm通过控制相似度矩阵的行稀疏解决噪音和离群点的干扰,使其具有更好的鲁棒性,最终可以实现样本自表达和稀疏相似度矩阵以及去除噪音、离群点的干扰相结合,提高子空间聚类的效果。本文将所提出的方法称为稀疏样本自表达子空间聚类算法,简称为SSR_SC(sparse sample self-representation for subspace clustering)。
1 相关理论高维数据一般可由多个低维结构表示,且具有很强相似度的样本往往在同一低维结构里,否则在不同的结构。每个低维结构对应为一个子空间,所以对数据的聚类可以通过对子空间的划分来聚类,即子空间聚类。
子空间聚类(subspace clustering)的定义:给定一个足够大的数据集X=[x1… xi… xn]∈Rd×n,其中xi表示一个具有d维属性的样本点,n为样本数。假设这些样本点是分别从k个不同的子空间Sii=1k(i=1, 2,…, k)里提取出来的,子空间聚类的目的就是将这些样本点正确地聚类到其所属的子空间。
目前基于谱聚类的子空间聚类算法的主要步骤是:1) 根据子空间策略构造样本集的相似度矩阵S ;2) 通过计算相似度矩阵或拉普拉斯矩阵的前k个特征值与特征向量,构建特征向量空间;3) 利用K-means算法对特征向量空间中的特征向量进行聚类,从而实现子空间的聚类。由上述的过程可知,该类方法的主要挑战就是构造一个良好的相似度矩阵S。而通过一个良好矩阵S得到的子空间的特征表现为:子空间内的样本具有高度的相似性,不同子空间的样本不相似或差异性大,且所有子空间呈块对角化结构[8]。
为了能构造一个良好的相似度矩阵而获得很好的子空间聚类效果,E. Elhamifar等[5]提出了稀疏子空间聚类算法SSC(sparse subspace clustering),将每个样本用空间里的其他样本来线性表示,通过L1-norm正则化项确保所获得的相似度矩阵是稀疏的。而Liu等[6]提出低秩自表达LRR(low-rank representation),通过核范数利用数据的全局信息寻找低秩样本自表达,并用L2, 1-norm项去除噪音和离群点,使所构造的相似度矩阵具有鲁棒性。由Lu等[7]提出的LSR(least squares regression),通过优化求解最小二乘回归的目标函数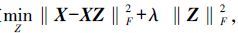
因此,本文提出了SSR_SC算法,充分利用样本间的相关性进行样本自表达,并通过L1-norm和L2, 1-norm正则化项对相似度矩阵进行稀疏约束,从而能很好地实现构造一个良好的相似度矩阵的目的。
2 SSR_SC算法对于样本空间X中的一个样本x,用同一空间中的其他样本对x进行线性表示的过程称为样本自表达。同一子空间中的样本之间往往具有很强的相关性,不同子空间的样本之间为无相关性或弱相关性,所以通过样本自表达能很好地利用样本之间的相关性来提高子空间聚类的效果。假设样本空间为X=[x1 x2 … xn]∈Rd×n,其中n为样本数,xi(i=1, 2, …, n)为具有d维属性的样本点。根据上述样本自表达的定义,即找出这样一个列向量zi∈Rn×1,使得xi可以通过Xzi表示。
但是样本空间X中往往存在噪音和离群点等干扰,其用e表示,则xi=Xzi+e,而这些干扰通常会影响子空间聚类的效果。因此本文算法希望找到这样一个相似度矩阵Z=[z1 z2 … zn]∈Rn×n,使得X与XZ的误差尽可能小。这通常可采用岭回归(ridge regression)实现:
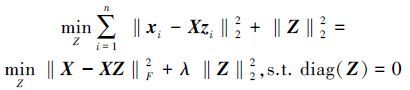 |
(1) |
式中:‖·‖F2为Frobenius范数,根据岭回归求解可得Z*=(XTX+λIn)-1XTX。但是这样得到的矩阵Z通常不稀疏,并且不能很好地解决噪音和离群点的干扰。因此本文算法利用L1-norm和L2, 1-norm替代目标函数(1) 中L2-norm,得到如下目标函数:
 |
(2) |
式中: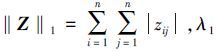
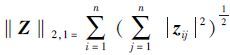
假定通过目标函数(2) 得到如下矩阵Z,其中diag(Z)=0,表明样本不能将自身作为相关性样本进行线性表示。
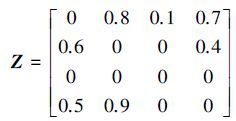 |
根据样本自表达定义可知,矩阵Z的第一列即样本x1,可以通过样本x2和样本x4线性表示,即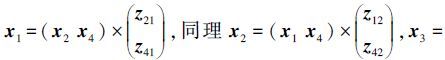
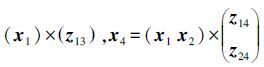
根据以上分析可知,本文提出的目标函数(2) ,不仅通过L1-norm确保每个样本都由与之具有强相关性的样本表示,而且利用L2, 1-norm避免噪音和离群点的干扰,使其具有更好的鲁棒性。注意,此时得到的相似度矩阵Z是稀疏的且充分考虑了样本间的相关性以及去除了噪音和离群点的干扰,然后通过矩阵Z构造矩阵S=(Z+ZT)/2,接着利用谱聚类算法进行最终的聚类,这样得到的子空间便具有了子空间内的样本相似性高,不同子空间的样本差异性大,且所有子空间呈块对角化结构的特征,很好地解决了基于谱聚类的子空间聚类问题中构造一个良好相似性矩阵的问题。
本文提出的SSR_SC算法的具体步骤如下:
算法1 SSR_SC算法
输入 参数λ1和λ2,以及样本空间:
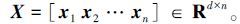 |
输出 聚类结果C∈Rn×1。
1) 根据算法2,迭代求解目标函数
2) 根据样本相似度矩阵Z去构造矩阵S=(Z+ZT)/2;
3) 利用谱聚类算法得到最终的聚类结果C∈Rn×1。
3 目标函数优化目标函数(2) 是一个凸函数,但是L1-norm和L2, 1-norm是非光滑的,无法直接求得解析解。为此,本文提出了一种有效的优化算法来解决这个问题,最后解出目标函数的最优化结果。
对目标函数(2) 中的Z的每一行Zi求导, 然后令其为0,得到式(3)
 |
(3) |
式中:Di(1≤i≤n)是一个对角矩阵,其第k个对角元素为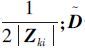
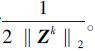
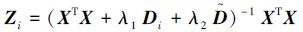 |
(4) |
此时,数据集XT和X已知,λ1和λ2为调制参数。但值得注意的是,Di和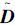
算法2 目标函数优化算法
输入 数据集X;
输出 Z(t)∈Rn×n;
初始化Z(1) ∈Rn×n,t=1;
do{
1) 计算对角矩阵Di(t)(1≤i≤n)和 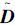
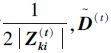
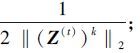
2) For每个i(1≤i≤n),计算
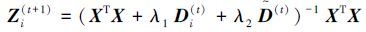 |
3) t=t+1;
}until收敛。
由上述算法2的描述知,优化目标函数的关键是目标值Zi(t+1) 要在迭代中收敛。下面证明目标函数(2) 的目标值在每一次迭代中都会减小。根据算法2的第2步,可得
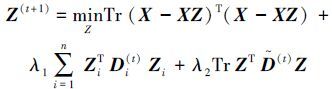 |
(5) |
由式(5) ,可得
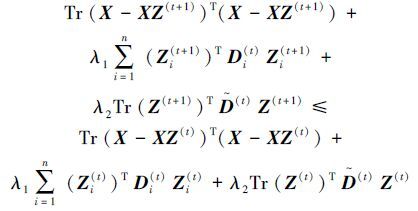 |
于是,可推导出
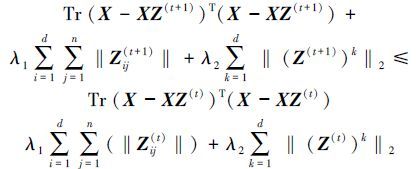 |
根据文献[14],对于任意向量Z和Z0,有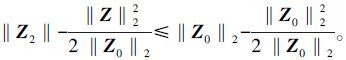
本文算法通过MATLAB语言编程,且所有实验都是在win7系统下的MATLAB 2014软件上运行测试。实验用到的数据集介绍如下。
Hopkins155[15]数据集被广泛用来测试各种子空间聚类算法。该数据集由156个视频序列组成,一个序列对应一个数据集,所以其共有156个数据集,并且每个序列中包含2或3个运动物体目标。
Jaffe[16]数据集由日本ATR表情识别研究协会提供,该数据集包含10个人的213张表情图像,每张表情图像经过预处理被裁剪为32像素×32像素大小的尺度。
USPS[17]数据集是由美国国家邮政局提供,数据集含有9 298个0~10的手写数字数据集,每个手写数字数据经预处理都被裁剪为16像素×16像素大小的尺度。用每个数字的前100个图像进行实验。
ORL[18]数据集是由剑桥Olivetti实验室提供,数据集包含40人的共400张面部图像,每张人脸数据经预处理被裁剪为16像素×16像素大小的尺度。
为了验证算法的性能,将目前较好的子空间聚类算法LSR、LRR和SSC与本文算法进行对比实验。为了保证算法的公平性,所有算法都没有对数据进行后期处理。
子空间聚类的重要挑战是处理存在于数据中的错误。因此,本文将子空间聚类错误率作为衡量各个算法性能的评价标准。其中,错误率越小,子空间聚类效果越好;反之,则越差。其定义为
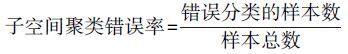 |
由于Hopkins155数据集包含156个不同的数据集,根据文献[19],本文将156个数据集中的子空间聚类错误率的最大值(Max)、均值(Mean)和中值(Median)以及标准差(Std)作为评价指标。对LSR,LRR,SSC以及本文算法SSR_SC在该数据集进行了对比,实验结果如表 1所示。
通过分析表 1可知,在Hopkins155数据集上,本文提出的SSR_SC比LSR、LRR和SSC获得了更好的子空间聚类效果。具体地,SSR_SC与LSR算法对比,错误率均值小2.38%,标准差小3.12%。LSR中使用L2-norm正则化项约束相似度矩阵Z,能使Z具有很好的块对角化结构,但是其并没有对Z稀疏而影响其最终的聚类效果。SSR_SC与LRR算法对比,最大错误率小7.16%,均值小3.30%,标准差小4.53%。其中LRR利用L2, 1-norm项惩罚相似度矩阵Z而可以去除噪音和离群点的影响,但是,其没有对Z稀疏。而本文提出的SSR_SC算法通过L2, 1-norm正则化项惩罚相似度矩阵而使其具有鲁棒性,且还对Z进行稀疏,所以能获得更好的子空间聚类效果。与SSC算法比较,本文算法SSR_SC也取得了更好的效果,最大错误率小0.96%,均值错误率小1.19%,标准差错误率小2.14%。Hopkins155数据集的大部分数据都是比较干净的,只有很小部分数据受到污染,这样的条件下SSC稀疏Z而更充分地利用了样本间的强相关性,从表 1中可以看到SSC比LRR的子空间聚类效果更好。
| 错误率 | LSR | LRR | SSC | SSR_SC |
| 最大值 | 0.397 1 | 0.476 4 | 0.414 4 | 0.404 8 |
| 平均值 | 0.042 1 | 0.051 3 | 0.030 2 | 0.018 3 |
| 中位数 | 0.005 2 | 0.005 3 | 0 | 0 |
| 标准差 | 0.086 0 | 0.100 1 | 0.076 2 | 0.054 8 |
4.2.2 数字图像和人脸图像上的实验
为了证明本文算法SSR_SC在实际数据集中也具有适用性,本文还在USPS、ORL以及Jaffe等数字图像和人脸图像数据集也进行了对比实验。实验结果如表 2所示。
| 数据集 | LSR | LRR | SSC | SSR_SC |
| USPS | 0.261 0 | 0.367 0 | 0.475 0 | 0.124 0 |
| ORL | 0.222 5 | 0.550 0 | 0.225 0 | 0.207 5 |
| Jaffe | 0.379 1 | 0.136 2 | 0.117 4 | 0.014 1 |
从表 2数据可知,SSR_SC算法在Jaffe数据集上取得了最优的效果,其子空间聚类错误率为1.41%,远远低于LSR,LRR和SSC 算法的错误率,效果与LRR和SSC相比提升了10倍,甚至比LSR算法提高了接近40倍。而在USPS和ORL数据集上同样也取得了较低的子空间聚类错误率,其中在USPS数据集上,相比LSR、LRR和SSC分别提高了13.70%、24.30%、35.10%;在ORL数据集上分别提高了1.50%、34.25%、1.75%。因此,可以认为本文提出的SSR_SC算法是一种高效的子空间聚类算法。
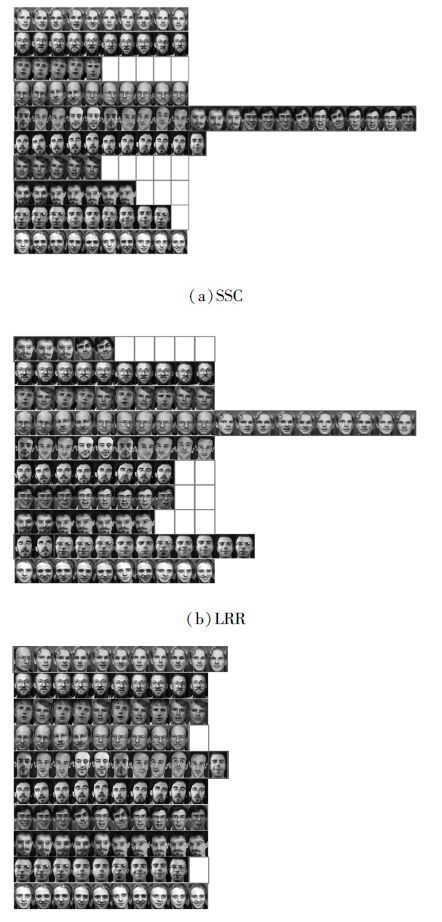
为了更加直观地对比LRR、SSC和SSR_SC算法的子空间聚类效果,选取ORL数据集里100张图片(10人,每人10张)进行实验,得到的实验结果如图 1所示。
|
| 图 1 SSC算法、LRR算法和SSR_SC算法分别对ORL数据集聚类的效果 Fig. 1 The subspace clustering effect of SSC, LRR and SSR_SC on ORL dataset |
图 1中,每行都代表一个子空间,短划线方框区域表示错误聚类的图片。从图 1可以直观的看出,本文提出的SSR_SC算法取得的子空间聚类效果明显好于LRR算法和SSC算法。其中,SSR_SC只将该数据集的2个人错误地聚类到其他子空间,而LRR和SSC算法聚类错误的图片数量分别为17张和19张,其中还存在将同一个人的图像平均的聚类为2个子空间的情况,如图 1(a)方点线方框所示,甚至出现将不同2组人聚类到同一个子空间的情况。综上分析,SSR_SC算法比现有的子空间聚类方法有更好的子空间聚类效果。
5 结束语提出一种综合稀疏学习和样本自表达的子空间聚类方法称为稀疏样本自表达算法。该算法通过充分考虑样本之间的相关性而进行样本自表达,并且通过稀疏学习理论进行优化,即通过L1-norm使相似度矩阵得到适当稀疏而让每个样本由与其相似性高的样本进行表达,通过L2, 1-norm解决样本自表达过程中噪音和离群点的干扰。与SSC算法和LRR算法比较,SSR_SC算法具有更好的鲁棒性和实现构造一个良好相似度矩阵的目的。此外,在Hopkinss155、USPS、ORL和Jaffe等数据集上实验的结果表明,SSR_SC算法在实际数据集,如运动目标分割和图像聚类等方面,能获得更好的子空间聚类效果。此后工作将提出的方法应用于更广泛的领域,如医学数据、文本数据以及金融数据等高维数据的聚类分析。
| [1] | 王卫卫, 李小平, 冯象初, 等. 稀疏子空间聚类综述[J]. 自动化学报 , 2015, 41 (8) : 1373-1384 WANG Weiwei, LI Xiaoping, FENG Xiangchu, et al. A survey on sparse subspace clustering[J]. Acta automatica sinica , 2015, 41 (8) : 1373-1384 |
| [2] | VIDAL R, MA Yi, SASTRY S. Generalized principal component analysis (GPCA)[J]. IEEE transactions on pattern analysis and machine intelligence , 2005, 27 (12) : 1945-1959 DOI:10.1109/TPAMI.2005.244 |
| [3] | TSENG P. Nearest q-flat to m points[J]. Journal of optimization theory and applications , 2000, 105 (1) : 249-252 DOI:10.1023/A:1004678431677 |
| [4] | FISCHLER M A, BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM , 1981, 24 (6) : 381-395 DOI:10.1145/358669.358692 |
| [5] | ELHAMIFAR E, VIDAL R. Sparse subspace clustering:algorithm, theory, and applications[J]. IEEE transactions on pattern analysis and machine intelligence , 2013, 35 (11) : 2765-2781 DOI:10.1109/TPAMI.2013.57 |
| [6] | LIU Guangcan, LIN Zhouchen, YAN Shuicheng, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE transactions on pattern analysis and machine intelligence , 2013, 35 (1) : 171-184 DOI:10.1109/TPAMI.2012.88 |
| [7] | LU Canyi, MIN Hai, ZHAO Zhongqiu, et al. Robust and efficient subspace segmentation via least squares regression[C]//Proceedings of the 12th European Conference on Computer Vision. Berlin Heidelberg, 2012:347-360. |
| [8] | FENG Jiashi, LIN Zhouchen, XU Huan, et al. Robust subspace segmentation with block-diagonal prior[C]//Proceedings of Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA, 2014:3818-3825. |
| [9] | 欧阳佩佩, 赵志刚, 刘桂峰. 一种改进的稀疏子空间聚类算法[J]. 青岛大学学报:自然科学版 , 2014, 27 (3) : 44-48 OUYANG Peipei, ZHAO Zhigang, LIU Guifeng. An improved sparse subspace clustering algorithm[J]. Journal of Qingdao university:natural science edition , 2014, 27 (3) : 44-48 |
| [10] | 杨国亮, 罗璐, 丰义琴, 等. 基于低秩稀疏图的结构保持投影算法[J]. 计算机工程与科学 , 2015, 37 (8) : 1584-1590 YANG Guoliang, LUO Lu, FENG Yiqin, et al. Structure preserving projection algorithm based on low rank and sparse graph[J]. Computer engineering and science , 2015, 37 (8) : 1584-1590 |
| [11] | ZHU Xiaofeng, HUANG Zi, YANG Yang, et al. Self-taught dimensionality reduction on the high-dimensional small-sized data[J]. Pattern recognition , 2013, 46 (1) : 215-229 DOI:10.1016/j.patcog.2012.07.018 |
| [12] | ZHANG Shichao, QIN Zhenxing, LING C X, et al. "Missing is useful":missing values in cost-sensitive decision trees[J]. IEEE transactions on knowledge and data engineering , 2005, 17 (12) : 1689-1693 DOI:10.1109/TKDE.2005.188 |
| [13] | ZHU Xiaofeng, HUANG Zi, CUI Jiangtao, et al. Video-to-shot tag propagation by graph sparse group lasso[J]. IEEE transactions on multimedia , 2013, 15 (3) : 633-646 DOI:10.1109/TMM.2012.2233723 |
| [14] | ZHU Xiaofeng, ZHANG Lei, HUANG Zi. A sparse embedding and least variance encoding approach to hashing[J]. IEEE transactions on image processing , 2014, 23 (9) : 3737-3750 DOI:10.1109/TIP.2014.2332764 |
| [15] | TRON R, VIDAL R. A benchmark for the comparison of 3-D motion segmentation algorithms[C]//Proceedings of Conference on Computer Vision and Pattern Recognition. Minneapolis, MN, USA, 2007:1-8. |
| [16] | LYONS M, AKAMATSU S, KAMACHI M, et al. Coding facial expressions with gabor wavelets[C]//Proceedings of the 3rd IEEE International Conference on Automatic Face and Gesture Recognition. Nara, 1998:200-205. |
| [17] | HULL J J. A database for handwritten text recognition research[J]. IEEE transactions on pattern analysis and machine intelligence , 1994, 16 (5) : 550-554 DOI:10.1109/34.291440 |
| [18] | SAMARIA F S, HARTERT A C. Parameterisation of a stochastic model for human face identification[C]//Proceedings of the 2nd IEEE Workshop on Applications of Computer Vision. Sarasota, FL, USA, 1994:138-142. |
| [19] | FENG Jiashi, LIN Zhouchen, XU Huan, et al. Robust subspace segmentation with block-diagonal prior[C]//Proceedings of Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA, 2014:3818-3825. |



