2. 计算智能与智能系统北京市重点实验室, 北京 100124;
3. 曼彻斯特大学 计算机科学学院, 曼彻斯特 M13 9PL
2. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China;
3. School of Computer Science, the University of Manchester, Manchester M13 9PL, UK
自从Zadeh教授于1965年创立模糊集理论[1]以来,以模糊集为基础的模糊系统在自动控制、信息处理等领域得到了广泛应用[2-4]。模糊集相似性分析是模糊系统研究的一个重要分支,得到众多学者的关注,在系统辨识与结构简化[5-15]、模式识别[16-17]、模糊聚类[18]等方面取得了丰硕的研究成果。
在模糊系统或模糊神经网络设计过程中,不但要计算模糊集相似性,而且要计算模糊规则相似性,以合并相似规则,进而获得简洁的网络结构,降低模型的复杂度。因此,模糊规则相似性分析与计算是模糊系统或模糊神经网络研究领域的关键问题之一。
目前,针对模糊规则相似性分析与计算的研究工作不多。Chao等[5]提出最小值模糊规则相似度计算方法,该方法通过计算每个输入变量隶属函数的相似度,将所有变量相似度的最小值作为模糊规则的相似度。Chen等[6]、Tsekouras[7]都采用该方法对模糊规则相似性进行计算。然而,在理论方面,该方法与常用的相似度定义不一致;在应用方面,该方法不能很好地区分模糊规则的相似性。
模糊规则相似性研究通常只考虑满足模糊集相似性的基本数学准则,而在模糊神经网络简化结构中,模糊规则相似性计算仅仅满足基本数学准则不足以满足应用的要求。
鉴于上述问题,文中提出4种模糊规则相似性计算方法,通过归纳应用中对模糊规则相似性的要求,提出3种应用性能评价指标——可区分性、维数依赖性和计算复杂性,并以此为基础,对各种相似性计算方法进行详细分析和比较。研究结果为模糊规则相似性分析及应用提供了依据。
1 模糊规则相似性计算问题描述 1.1 问题描述讨论模糊规则相似性计算问题之前,首先给出常用的模糊集相似性定义[5, 8]。
定义1 模糊集相似性。假设A和B分别为论域U上的模糊集,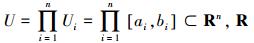
 |
(1) |
式中:S(A, B) 表示A和B的相似度;M (A∩B) 表示A和B交集的面积;M (A∪B) 表示A和B并集的面积。
在模糊规则相似性计算问题中,假设一对模糊规则RA和RB表述如下。
 |
(2) |
 |
(3) |
式中:xi∈Ui R是第i个输入变量;Ui是其相应输入变量空间;Ai和Bi是关于输入变量xi的模糊集,其相应隶属函数分别为uAi(xi) 和uBi(xi),i=1, 2, …, n;x=(x1, …, xn),n为输入变量个数;wA(x) 和wB(x) 是模糊规则的结论。当给定一个Mamdani型系统或网络时,wA (x)=CA;当给定一个T-S型时,wA(x)=CA0+CA1x1+…+CAnxn,其中Cj(j=A, A0, …, An) 为常数。
由于一对模糊规则涉及两组模糊集,无法直接应用定义1给出的模糊集相似性计算模糊规则的相似性。因此,引入多变量模糊集对上述规则RA和RB重新表述如下。
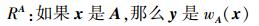 |
(4) |
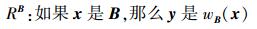 |
(5) |
式中:A和B为输入空间U上两个多变量模糊集;A=A1×A2×…×An,B =B1×B2×…×Bn,相应规则的激活强度分别为
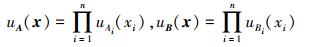 |
(6) |
模糊规则RA和RB的相似性定义为,在输入空间U上两个多变量模糊集A和B的相似性。
因此,通过引用多变量模糊集的概念,将两条模糊规则的相似性等价地转换成两个多变量模糊集的相似性,而如何计算模糊规则RA和R B的相似度S(A, B) 是需要解决的问题。
1.2 性能评价指标由于模糊规则相似性等价于多变量模糊集相似性,因此也必须满足模糊集相似性的基本数学准则[8-9],归纳如下。
模糊规则相似性S(A, B) 的基本数学准则如下。
1) 正则性:0≤S(A, B)≤1。
2) 对称性:S(A, B)=S(B, A)。
3) 不相交模糊规则的相似度应为0,即
S(A, B)=0 uA (x)uB(x)=0, x∈U。
4) 相交模糊规则的相似度应大于0,即
S(A, B)>0 x∈U, uA(x)uB(x)>0。
当相似度为1时,两条模糊规则是完全相同的,即
S(A, B)=1 uA(x)=uB(x), x∈U
5) 缩放或移位下的不变性,即
S(A′, B′)=S(A, B) uA′ (l+kx)=uA(x),
uB′(l+kx)=uB(x), l∈Rn, k∈R, k>0。
然而,将模糊规则相似性计算方法应用于模糊神经网络结构简化时,不但要满足基本数学准则,而且要满足实际应用的要求。为此,提出以下3种评价指标。
1.2.1 可区分性可区分性是指对两个明显不同模糊规则,其相应相似度能够反映出模糊规则的不同。可区分性可被看作相似度定义的灵敏度性能指标,区分性好的相似度具有较高的灵敏度。该指标能够更好地辨识出相似度高或低的模糊规则。
1.2.2 维数依赖性维数依赖性是指模糊规则相似度值是否会随着维数的增加或减少而变化。维数依赖性是模糊规则相似度辨识与合并中非常重要的性能指标。如果相似度的定义具有维数依赖性,对每个不同维数的系统辨识需要大量数据和实验才能确定合适的相似度阈值,给实际应用带来一定困难;如果相似度计算不依赖系统维数的变化而变化,可确定一个通用的相似度阈值,用于各种不同维数的模糊系统或网络进行结构简化。
1.2.3 计算复杂性计算复杂性是指计算模糊规则相似度所需的步骤和时间。如果模糊规则相似度计算过于复杂,会影响计算的有效性,限制算法的可用性。
2 计算方法与性能分析 2.1 最小值方法最小值方法[5-7]将所有输入变量xi(i=1, 2, …, n) 相应模糊集相似度的最小值作为模糊规则的相似度,其计算公式如下:
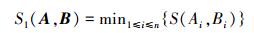 |
(7) |
首先,可证明基于最小值的模糊规则相似度计算方法满足相似性的基本数学准则;其次,计算简单,当得到每个输入变量相应单变量模糊集的相似度S(Ai, Bi) 后,取最小值运算即可得到模糊规则的相似度;最后,该方法取值仅取决于某个输入变量相应模糊集的相似度,不具有维数依赖性。
然而,由式 (7) 可知,该方法与相似度定义 (式 (1)) 不一致,且可区分性较差。例如,有两条模糊规则,其相应输入变量xi的模糊集合分别为Ai和Bi(i=1, 2, 3),考虑以下两种情况。情况1:每个变量相应模糊集的相似度均相同,即S(Ai, Bi)=0.4, (i=1, 2, 3),采用最小值方法,这两条规则的相似度为S1(A, B)=0.4。情况2:各变量相应模糊集的相似度分别为S (A1, B1)=0.4,S(A2, B2)=0.9,S(A3, B3)=0.9,采用最小值方法,这两条规则的相似度仍为0.4。结果显示,在第2种情况下,两条模糊规则的相似度明显大于第一种情况的相似度。因此,最小值方法不能很好地区分模糊规则间的明显差异,在一定程度上影响相似度的有效判定。
2.2 乘积方法及其改进方法针对最小值方法存在可区分性差的问题,提出了乘积方法,该方法是对最小值方法的改进,通过计算所有输入变量相应模糊集相似度的乘积得到模糊规则的相似度,即
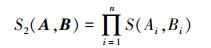 |
(8) |
首先,可证明乘积法满足相似性的基本数学准则;其次,乘积方法计算简单,且可区分性较好。如上例,采用乘积方法,在两种情况下,两条模糊规则的相似度分别为0.064和0.324。结果表明,第2种情况比第1种情况下的模糊规则具有更高的相似度。因此,乘积方法能够更好地区分模糊规则的相似性。
然而,由式 (8) 可知,乘积方法仍然与相似度定义1不一致,是一种直观方法。而且,由于相似度取值范围为[0,1],随着维度不断增加,相似度越来越小。如上例,在第1种情况下,每个单变量模糊集的相似度均为0.4,n维变量模糊规则相似度为 (0.4)n,当维数逐渐增加时,得到的相似度呈现递减的趋势。
为了克服乘积法具有维数依赖性的缺点,提出了一种改进的方法 (第3种方法),即
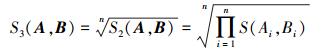 |
(9) |
该方法继承了乘积方法满足基本数学准则、计算简单和可区分性好的优点,克服了维数依赖性的不足。如上例,当每个变量模糊集的相似度均为0.4时,无论维数如何增加,模糊规则的相似度仍为
 |
即相似度不随维数的变化而变化。
综上所述,改进的乘积方法是一种比较理想的模糊规则相似度计算方法,不足之处在于该方法是一种直观的方法,不满足常用的相似度定义。
2.3 交并面积和比值法根据模糊集相似度定义[5, 8]的直观意义,两条模糊规则总交集的面积可定义为每个输入变量相应的一对模糊集的交集面积之和。同理,其总并集的面积可定义为每个输入变量相应的一对模糊集的并集面积之和,从而类似于定义1,模糊规则相似性定义为交集面积之和与并集面积之和的比值。因此,将该方法 (即第4种方法) 命名为交并面积和比值法,其计算公式为
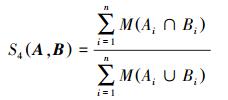 |
(10) |
其中
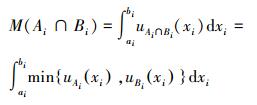 |
(11) |
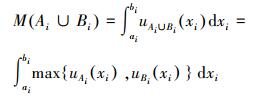 |
(12) |
首先,由式 (10)~(12) 可以证明,该方法满足相似性的基本数学准则;其次,计算简单,当得到每个输入变量相应模糊集的交集与并集面积后,通过简单的求和与比值运算即可得到模糊规则的相似度。而且,该方法不具有维数依赖性。例如,在n维空间的两条模糊规则,每对单变量模糊集Ai和Bi(i=1, 2, …, n) 的交集面积为0.4,并集面积为0.8,则当n=1时,这两条规则的相似度为0.5;当n>1时,相似度为
 |
即随着输入空间维数的变化,模糊规则相似度不会随之变化。
此外,该方法具有很好的可区分性。例如,一对两维模糊规则的单变量交集与并集面积分别为
M(A1∩B1)=M(A2∩B2)=0.4
M(A1∩B1)=M(A2∩B2)=0.8
则根据式 (10) 得到这对模糊规则的相似度为0.5。假定另一对模糊规则的单变量交集与并集面积分别为
M(A1∩B1)=0.4, M(A1∪B1)=0.8
M(A2∩B2)=0.35, M(A2∪B2)=0.8
则相似度为0.47。因此,该方法能够很好地区分模糊规则的相似性。
综上所述,交并面积和比值法是一种较理想、具有很好直观意义的模糊规则相似度计算方法,而且在一定程度上接近于常用的相似度定义。
2.4 交并总面积比值法及其改进方法第5种方法是作者前期提出的交并总面积比值法,其相似度计算公式如下[19]:
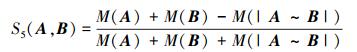 |
(13) |
式中
 |
(14) |
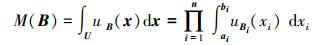 |
(15) |
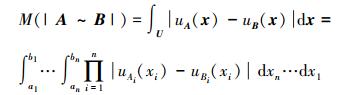 |
(16) |
首先,由式 (13)~(16) 可知,该方法与相似度定义一致;其次,该方法满足相似性的基本数学准则 (证明过程见附录)。而且,由于模糊规则或多变量模糊集A和B之间的任何不同之处都可通过M (|A~B|) 体现,导致式 (13) 定义的S (A, B) 不同。因此,该方法具有很好的可区分性。
尽管该方法具有上述优点,但严格遵循常用的模糊集相似性定义却存在不容忽视的缺点。首先,计算较为复杂。计算M(|A~B|) 涉及多重积分,而高维多重数值积分至今仍是一个尚未有效解决的问题。其次,具有维数依赖性。例如,在输入空间U=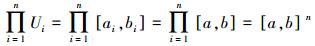
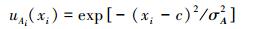 |
(17) |
 |
(18) |
式中:c为两个高斯函数的中心;σA和σB分别为两个高斯函数的宽度,且σA>σB>0。于是,
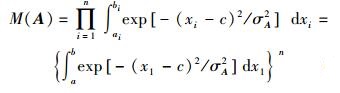 |
(19) |
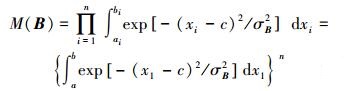 |
(20) |
M(|A~B|) 如式 (16) 所示。由于σA>σB >0,推出
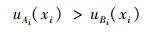 |
(21) |
因此得出
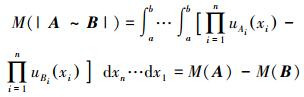 |
(22) |
代入式 (13) 得到:
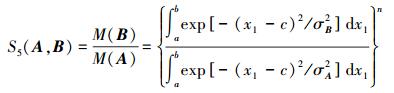 |
(23) |
由式 (21) 得出:
 |
(24) |
因此,由式 (23) 可推出,当n→∞时,
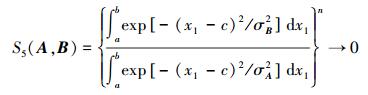 |
(25) |
即无论Ai和Bi多相似,只要它们不相同 (即相似度小于1),当输入空间维数逐渐增加时,A和B的相似度会逐渐减小;当输入空间维数趋于无穷时,相似度趋于0。
为了克服维数依赖性的缺点,提出一种改进的交并总面积比值法 (即第6种方法),如下式所示:
 |
(26) |
该方法满足相似性基本数学准则,具有很好的可区分性,且不具有维数依赖性。如上例,采用该方法计算式 (23) 可得到:
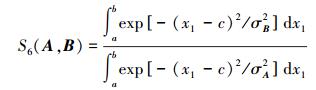 |
(27) |
因此,得到的相似度不随维数的变化而变化。
需要指出的是,改进的交并总面积比值法仍存在计算复杂的缺点。同时,该方法不再满足常用的相似性定义。
2.5 6种方法的性能比较上述分析和比较结果显示,6种方法都满足相似性定义的基本数学准则。在应用性能指标方面,每种方法各有不同。表 1给出了这6种方法在3个性能指标方面的比较结果。
| 方法 | 可区分性 | 维度依赖性 | 计算复杂性 |
| 最小值方法 | 最差 | 否 | 简单 |
| 乘积方法 | 较好 | 是 | 简单 |
| 改进的乘积方法 | 较好 | 否 | 简单 |
| 交并面积和比值法 | 较好 | 否 | 简单 |
| 交并总面积比值法 | 较好 | 是 | 复杂 |
| 改进的交并总面积比值法 | 较好 | 否 | 复杂 |
由表 1可知,改进的乘积方法与交并面积和比值法是两种比较理想的模糊规则相似性计算方法。
3 仿真实验本文所做的实验研究均是基于Matlab R2014a在Intel © CoreTM 2 Duo CPU 3 GHz,内存2 GB的普通PC机上进行的。
3.1 实验1假设有3个输入变量 (x1, x2, x3)、6条模糊规则 (R1, R2, R3, R4, R5, R6),高斯函数中心 (c) 和宽度 (σ) 如表 2所示。分别采用最小值法、乘积法、改进乘积法、交并面积和比值法、改进交并面积和比值法、交并总面积比值法及改进交并总面积比值法共6种方法对模糊规则相似性进行计算,其中单变量相似性计算方法采用文献[20]提出的方法。得到的相似度及相应的运行时间如表 3所示,采用最小值方法得到部分规则相似度如表 4所示,其中,Sij代表第i和第j条规则的相似度,M1~M6依次代表上述6种相似性计算方法。
| c/σ | x1 | x2 | x3 |
| R1 | 2.547 6/1.334 2 | 1.204 4/4.813 8 | 2.786 2/1.564 0 |
| R2 | 3.821 2/3.694 9 | 1.034 4/ 4.613 8 | 2.691 1/2.740 7 |
| R3 | 1.395 2/5.591 3 | 1.020 4/5.272 2 | 1.654 0/3.359 7 |
| R4 | 2.952 3/1.833 6 | 1.877 4/2.249 8 | 2.171 8/1.397 7 |
| R5 | 3.541 6/1.623 0 | 1.653 0/4.074 5 | 2.014 4/4.410 1 |
| R6 | 2.037 7/1.068 5 | 1.905 7/1.243 1 | 3.237 6/3.626 4 |
| M1 | M2 | M3 | M4 | M5 | M6 | |
| S12 | 0.343 | 0.186 | 0.571 | 0.658 | 0.210 | 0.594 |
| S13 | 0.237 | 0.094 | 0.455 | 0.534 | 0.100 | 0.465 |
| S14 | 0.465 | 0.200 | 0.586 | 0.549 | 0.357 | 0.710 |
| S15 | 0.352 | 0.137 | 0.515 | 0.580 | 0.234 | 0.616 |
| S16 | 0.257 | 0.068 | 0.409 | 0.374 | 0.195 | 0.580 |
| S23 | 0.535 | 0.318 | 0.682 | 0.690 | 0.402 | 0.738 |
| S24 | 0.482 | 0.118 | 0.490 | 0.488 | 0.123 | 0.497 |
| S25 | 0.439 | 0.227 | 0.610 | 0.647 | 0.387 | 0.729 |
| S26 | 0.258 | 0.051 | 0.371 | 0.408 | 0.084 | 0.438 |
| S34 | 0.320 | 0.056 | 0.383 | 0.380 | 0.058 | 0.387 |
| S35 | 0.274 | 0.158 | 0.541 | 0.582 | 0.237 | 0.619 |
| S36 | 0.191 | 0.027 | 0.299 | 0.323 | 0.042 | 0.349 |
| S45 | 0.317 | 0.119 | 0.495 | 0.479 | 0.174 | 0.558 |
| S46 | 0.373 | 0.095 | 0.456 | 0.446 | 0.243 | 0.624 |
| S56 | 0.274 | 0.059 | 0.389 | 0.472 | 0.109 | 0.478 |
| 时间/s | 0.085 | 0.084 | 0.092 | 0.084 | 376.69 | 379.32 |
| x1 | x2 | x3 | |
| S12 | 0.343 | 0.951 | 0.571 |
| S15 | 0.465 | 0.836 | 0.352 |
| S25 | 0.439 | 0.840 | 0.615 |
从3个应用性能指标方面对实验结果进行进一步分析。
3.1.1 可区分性由表 2可知,对变量x1而言,在规则R1中其值近似于2.547 6 (即其中心),而在R2和R5中,其值近似于3.821 2和3.541 6。因此,与R1最不相似的是R2和R5。对于变量x2和x3而言,相比R1与R5,R1与R2则较为相似。然而,由表 3及表 4可知,对最小值方法而言,相似度S12和S15完全取决于在各个变量中最不相似模糊集的相似度,即0.343与0.352,如表 3所示,最小值方法得到的S12和S15较为接近,其余5种方法得到的S12和S15均呈现出差异。因此,该实验表明最小值法的可区分性较差,而另5种方法在一定程度上克服了这一缺点。
3.1.2 维数依赖性由表 3可知,方法M2和M5所得到的模糊规则相似度都小于0.5。通常相似度大于0.5才能进行规则合并。如果采用方法M2或M5,则没有一对规则需要进行合并,而通过相应的改进方法M3或M6,该缺陷得到了明显的改善,多对模糊规则都显示出很好的相似性。
此外,对任何一对模糊规则,方法M2的相似度都小于方法M5的相似度,因此,方法M2比M5维数依赖性更强。
3.1.3 计算复杂性表 3显示,方法M1、M2、M3和M4的运行时间短,计算简单,而方法M5与M6则较复杂。对于一个三维输入、6条规则的模糊神经网络,方法M5与M6的计算时间是方法M1、M2、M3和M4的4 000多倍。对于更加高维和具有更多规则的模糊系统或模糊神经网络,计算时间会更长。因此,方法M5与M6不适用于高维复杂系统的结构简化。
实验结果表明,改进的乘积方法与交并面积和比值法是较理想的模糊规则相似性计算方法。
3.2 实验2假设有4个输入变量 (x1, x2, x3, x4)、一对模糊规则 (R1, R2),高斯函数中心 (c) 和宽度 (σ) 如表 5所示。与实验1类似,分别采用最小值法等六种方法对模糊规则相似性进行计算,得到的相似度及相应的运行时间如表 6所示,其中,S12代表两条规则的相似度,M1、M2、M3、M4、M5和M6依次代表 6种相似性计算方法。
| c/σ | R1 | R2 |
| x1 | 0.587 0/0.364 3 | 0.413 9/0.532 3 |
| x2 | 0.309 1/0.711 7 | 0.263 8/0.871 5 |
| x3 | 0.758 8/0.328 7 | 0.995 2/0.650 1 |
| x4 | 0.186 6/0.974 8 | 0.781 1/0.076 0 |
| S12 | 时间/s | |
| M1 | 0.066 | 0.036 |
| M2 | 0.015 | 0.037 |
| M3 | 0.352 | 0.038 |
| M4 | 0.463 | 0.038 |
| M5 | 0.067 | 1 359.807 |
| M6 | 0.508 | 1 366.569 |
由表 6可知,与方法M3、M4和M6相比,方法M2与M5得到的模糊规则相似度小很多,表明这两种方法具有维数依赖性。在运行时间方面,相比前4种方法,方法M5与M6计算较为复杂。因此,实验结果进一步表明,改进的乘积方法与交并面积和比值法不具有维数依赖性,计算较为简单,是较理想的模糊规则相似性计算方法。
3.3 实验3该实验以三角形隶属函数为例。假设有3个输入变量 (x1, x2, x3), 一对模糊规则 (R1, R2),三角形函数的参数包括下部左顶点 (p1)、上部顶点 (q) 和下部右顶点 (p2) 值如表 7所示。与实验1和实验2类似,采用最小值法等6种方法计算得到的规则相似度及相应的运行时间如表 8所示。
| p1/q/p2 | R1 | R2 |
| x1 | 3.5/4/4.5 | 3/4/5 |
| x2 | 2.5/4/5.5 | 2/4/6 |
| x3 | 1.5/4/6.5 | 1/4/7 |
| S12 | 时间/s | |
| M1 | 0.500 | 0.037 |
| M2 | 0.313 | 0.043 |
| M3 | 0.679 | 0.043 |
| M4 | 0.750 | 0.050 |
| M5 | 0.312 | 1 536.931 |
| M6 | 0.679 | 1 564.911 |
由实验结果可知,6种模糊规则相似性计算方法不但适用于高斯隶属函数,而且适用于三角形隶属函数,具有很好的通用性。在维数依赖性方面,方法M2与M5得到的模糊规则相似度较小,表明这两种方法具有维数依赖性。在运行时间上,方法M5与M6计算较为复杂。
因此,实验结果进一步表明,改进的乘积方法与交并面积和比值法不具有维数依赖性,计算简单,是较理想的模糊规则相似性计算方法。而且,基于文中分析与讨论,交并面积和比值法具有更好的直观性,更接近常用的相似度定义。
4 结束语本文对模糊规则相似性计算进行了研究。首先,证明了模糊规则相似性等价于多变量模糊集的相似性,并提出了3种应用性能评价指标——可区分性、维数依赖性和计算复杂性。其次,在现有两种模糊规则相似性计算方法的基础上,提出了4种相似性计算方法,进行了详细分析和比较。分析和比较结果表明,提出的交并面积和比值法,可区分性好,不具有维数依赖性,计算简单、直观,是一种比较理想的模糊规则相似性计算方法。最后,为更好地说明最小值法等六种方法的优缺点,给出了数值分析实例,并对实验结果进一步分析。
文中的研究具有以下几方面意义:1) 证明了模糊规则相似性等价于多变量模糊集相似性;2) 证明了常用的模糊集相似性定义在应用于模糊规则相似性计算中也存在不足之处,证实了对模糊规则相似性进一步研究的必要性;3) 研究结果为模糊规则相似性分析和计算方法选取提供了依据,尤其是为基于模糊规则相似性分析与合并的模糊神经网络结构简化提供了方法基础和设计思路。
为了有效改善目前模糊规则相似性在计算有效性和精确性方面的不足,将提出的各种方法应用于模糊神经网络结构简化是下一步要进行的研究工作。
附录交并总面积比值法满足相似性基本数学准则的定理如下。
定理 假设多变量模糊集A和B的相应规则的激活强度分别如式 (6) 所示,且uAi(xi) 和uBi(xi) 是U=U1×U2×…×Un上的连续函数,则由式 (13)~(16) 给出的相似度计算方法满足相似性的基本数学准则。
证明 由于该方法对准则 (1) 和准则 (2) 显然成立,因此,仅证明准则 (3)~准则 (5) 成立。
准则(3):由于uA(x)≥0,uB(x)≥0,在U上连续,则
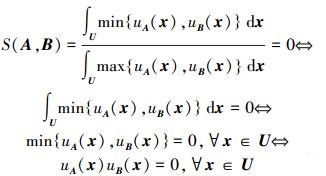 |
(A.1) |
准则(4):由于uA(x)≥0,uB(x)≥0,在U上连续, 则
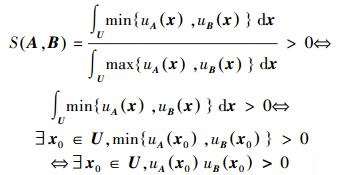 |
(A.2) |
而且, 根据式 (13)~(16),得到
 |
(A.3) |
准则(5):
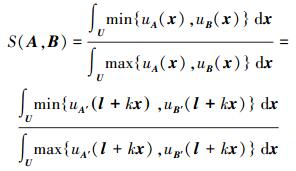 |
(A.4) |
作积分变换y=l+kx,则上式变为
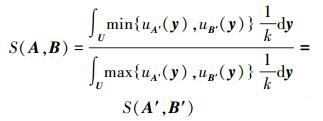 |
(A.5) |
证明完毕。
| [1] | ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X. |
| [2] | TÜRKSEN I B, FAZEL ZARANDI M H. Fuzzy system models for aggregate scheduling analysis[J]. International Journal of approximate reasoning, 1998, 19(1/2): 119-143. |
| [3] | FAY A. A fuzzy knowledge-based system for railway traffic control[J]. Engineering applications of artificial intelligence, 2000, 13(6): 719-729. DOI:10.1016/S0952-1976(00)00027-0. |
| [4] | GE Aaidong, WANG Yuzhen, WEI Airong, et al. Control design for multi-variable fuzzy systems with application to parallel hybrid electric vehicles[J]. Control theory & applications, 2013, 30(8): 998-1004. |
| [5] | CHAO C T, CHEN Y J, TENG C C. Simplification of fuzzy-neural systems using similarity analysis[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 1996, 26(2): 344-354. DOI:10.1109/3477.485887. |
| [6] | CHEN Minyou, LINKENS D A. Rule-base self-generation and simplification for data-driven fuzzy models[J]. Fuzzy sets and systems, 2004, 142(2): 243-265. DOI:10.1016/S0165-0114(03)00160-X. |
| [7] | TSEKOURAS G E. Fuzzy rule base simplification using multidimensional scaling and constrained optimization[J]. Fuzzy sets and systems, 2016, 297: 46-72. DOI:10.1016/j.fss.2015.10.009. |
| [8] | SETNES M, BABUSKA R, KAYMAK U, et al. Similarity measures in fuzzy rule base simplification[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 1998, 28(3): 376-386. DOI:10.1109/3477.678632. |
| [9] | REZAEE B. Rule base simplification by using a similarity measure of fuzzy sets[J]. Journal of intelligent & fuzzy systems: applications in engineering and technology, 2012, 23(5): 193-201. |
| [10] | PRATAMA M, ANAVATTI S G, LUGHOFER E. GENEFIS: toward an effective localist network[J]. IEEE transactions on fuzzy systems, 2014, 22(3): 547-562. DOI:10.1109/TFUZZ.2013.2264938. |
| [11] | LIN C T, LEE C S G. Reinforcement structure/parameter learning for neural-network-based fuzzy logic control systems[J]. IEEE transactions on fuzzy systems, 1994, 2(1): 46-63. DOI:10.1109/91.273126. |
| [12] | LENG Gang, ZENG Xiaojun, KEANE J A. A hybrid learning algorithm with a similarity-based pruning strategy for self-adaptive neuro-fuzzy systems[J]. Applied soft computing, 2009, 9(4): 1354-1366. DOI:10.1016/j.asoc.2009.05.006. |
| [13] | HAN Honggui, QIAO Junfei. A self-organizing fuzzy neural network based on a growing-and-pruning algorithm[J]. IEEE transactions on fuzzy systems, 2010, 18(6): 1129-1143. DOI:10.1109/TFUZZ.2010.2070841. |
| [14] | WANG Xiaojing, ZOU Zhihong, ZOU Hui. Water quality evaluation of Haihe River with fuzzy similarity measure methods[J]. Journal of environmental sciences, 2013, 25(10): 2041-2046. DOI:10.1016/S1001-0742(12)60260-5. |
| [15] | NGUYEN N N, ZHOU W J, QUEK C. GSETSK: a generic self-evolving TSK fuzzy neural network with a novel Hebbian-based rule reduction approach[J]. Applied soft computing, 2015, 35: 29-42. DOI:10.1016/j.asoc.2015.06.008. |
| [16] | ROUBENS M. Pattern classification problems and fuzzy sets[J]. Fuzzy sets and systems, 1978, 1(4): 239-253. DOI:10.1016/0165-0114(78)90016-7. |
| [17] | DENG Yong, SHI Wenkang, DU Feng, et al. A new similarity measure of generalized fuzzy numbers and its application to pattern recognition[J]. Pattern recognition letters, 2004, 25(8): 875-883. DOI:10.1016/j.patrec.2004.01.019. |
| [18] | CASTELLANO G, FANELLI A M, MENCAR C, et al. Similarity-based Fuzzy clustering for user profiling[C]//Proceedings of 2007 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology Workshops. Silicon Valley, USA, 2007: 75-78. |
| [19] | QIAO Junfei, LI Wei, ZENG Xiaojun, et al. Identification of fuzzy neural networks by forward recursive input-output clustering and accurate similarity analysis[J]. Applied soft computing, 2016, 49: 524-543. DOI:10.1016/j.asoc.2016.08.009. |
| [20] | LI Wei, QIAO Junfei, ZENG Xiaojun. Accurate similarity analysis and computing of Gaussian membership functions for FNN simplification[C]//Proceedings of the 12th International Conference on Fuzzy Systems and Knowledge Discovery. Zhangjiajie, China, 2015: 402-409. |



