互联网时代,随着社交网络、电子商务与移动通信等技术的蓬勃发展,人类社会进入以PB级数据信息为特征的大数据时代。如何从海量复杂数据集中自动发现新知识、新规律,实现从数据到知识到决策的挑战与跨越[1-2],成为各行各业普遍面临的严峻技术挑战。
所谓聚类, 就是根据描述事物的某些属性, 将事物聚集成若干类,使得类间相似性尽量小,类内相似性尽量大[3]。与分类不同,聚类无须明确的类标记,无须区分训练集与测试集,是一种寻求数据自然聚簇结构的非监督学习方法,可以产生问题中数据的概括性描述,可以自动构建分类层次结构,具有更好的普适性;同时,聚类又具有不确定性。对于给定的数据集,聚类结果不仅依赖于实际的数据分布,而且取决于问题的应用背景与目标,不存在唯一正确的聚类划分。正由于这种普适性与不确定性,使聚类问题比分类问题更复杂、更具挑战性,被认为是大数据分析与数据挖掘的基础问题,也成为统计、模式识别、机器学习、人工智能等诸多学科领域中一个非常活跃且非常重要的研究热点[3-5]。
2014年《Science》杂志上刊登了一篇题为《Clustering by fast search and find of density peaks》的论文[1],论文提出一种快速搜索和发现密度峰值的聚类算法。算法将具有局部极大密度估计值的样本点视为聚类中心,通过快速搜索聚类中心,将每一个非中心样本点沿着密度递增的最近邻方向迭代划分给相应的聚类中心,实现数据划分。算法思路新颖,简单实用,具有良好的聚类质量,能够发现任意形状、大小和密度的聚类,能够有效处理噪声和离群数据,对人脸等高维非结构化数据具有良好的适用性。虽然论文的局限性遭到众多读者的质疑,如聚类结果严重依赖于密度参数dc的仔细选择,但整体上可以为聚类算法设计提供一种新思路。
本文深入探讨了快速搜索密度峰值点的聚类算法[1]的局限性,引入基于密度估计熵最小化的自适应参数优化方法弥补其核函数及其参数值人为确定的羁绊,提出一种改进的搜索密度峰值点的聚类算法。在重现论文算法并获得与原作者相同实验结果的基础上,用改进算法重新聚类。对比实验结果表明,改进算法不仅能有效解决原算法的参数优选问题,而且具有相对更好的聚类性能。
1 快速搜索密度峰值的聚类算法给定数据集D={x1, x2, …, xn},快速搜索密度峰值点的聚类算法[1]。假设聚类中心对应某些具有局部极大密度估计值的样本点,这些样本点可以看作由低密度样本点所包围的“高密度峰值点”,距离其他高密度近邻样本相对较远。算法通过快速搜索和发现代表聚类中心的“高密度峰值点”,将每个非中心样本点沿着密度估计值递增的最近邻方向迭代移动到相应的聚类中心,实现数据划分。这里涉及两个基本概念:局部密度估计和高密度最近邻距离。
1.1 局部密度估计与高密度最近邻距离∀xi∈D, 1≤i≤n, 局部密度估计值dc定义为
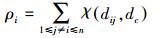 |
(1) |
式中:χ(·) 相当于核密度估计的核函数,论文给出3种可选的核函数形态,相应的密度估计公式如下:
1) 截断核估计
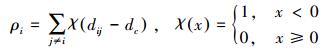 |
(2) |
2) 高斯核估计
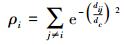 |
(3) |
3) 指数核估计
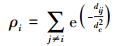 |
(4) |
式中:dij为样本点xi、xj间的距离,采用满足三角不等式的距离度量,如欧氏距离;dc>0是预先指定的密度估计参数,相当于核函数的窗宽。
高密度最近邻距离δi则定义为xi到具有更大密度估计值的最近邻样本点的距离,即
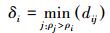 |
(5) |
显然,具有全局最大密度估计值的样本点不存在高密度最近邻,可简单地令其高密度最近邻距离等于所有样本点间距离的最大值。
1.2 基于决策图的聚类划分通过计算每个样本点xi(1≤i≤n) 的局部密度估计值dc和高密度最近邻距离δi,算法将原始数据集D映射到由局部密度估计ρ和高密度最近邻距离δ组成的二维特征空间中。直觉上,代表聚类中心的样本点应同时具有较大的局部密度估计值ρ和较大的高密度最近邻距离ρ。由此,通过特征空间中决策图的可视化,可以实现基于中心的聚类划分。
图 1所示为论文实验采用的模拟测试数据集及其聚类结果[1]。测试数据包含4 000个样本点,分别取自6个不同的二维正态分布,还有一些噪声数据。图 1(a)所示为采用式 (2) 所示的截断核估计且参数dc取最小2%的距离做截断时 (即dc取值为所有样本点间距离的最小2%的距离中的最大距离),测试数据集投影到以局部密度估计ρ值为横轴、以高密度最近邻距离δ为纵轴的二维空间中形成的决策图[1];显然,图中虚线框选出的5个样本点同时具有较大的局部密度估计值ρ和高密度最近邻距离ρ,可以被选为5个聚类中心,相应聚类结果如图 1(b)所示。4 000个样本点被划分为5个类和噪声数据,每个类用与中心样本点相同的数字来标记。其中,第五类最大,包含多于1 500个样本点,第一类最小,仅有200多个样本点。显然,算法具有良好的聚类质量,可以发现不同形状、大小和密度的聚类,可以有效处理噪声数据。
|
| 图 1 包含4 000个样本点的测试数据集的聚类结果 Fig. 1 The clustering results of the test dataset containing 4 000 sample points |
但算法中存在一个重要参数,即密度参数dc。论文认为,参数dc的取值虽然会影响样本点的局部密度估计与高密度最近邻距离,但不会严重影响最终的聚类结果,通常选取所有样本点间距离的最小1%~2%做截断即可 (即令dc取值为所有样本点间距离的最小1%~2%的距离中的最大距离)。但重现论文算法及其实验结果时,我们发现,核函数的选择及其参数dc的取值都会严重影响最终聚类结果。
1.3 核函数及其参数选择对聚类结果的影响图 2所示为常用的两个标准测试数据集。
|
| 图 2 两个标准测试数据集 Fig. 2 Two standard test datasets: aggregation and spiral |
图 2中,aggregation数据集[9]包含7个不同大小、形状和密度的聚类,共788个样本点;spiral数据集[10]包含3个螺旋形聚类,共312个样本点。
采用快速搜索密度峰值点的聚类算法对其进行聚类分析,聚类结果分别如图 3、4、5所示。

|
| 图 3 aggregation数据集的聚类结果 Fig. 3 The clustering results for aggregation datasets |
|
| 图 4 spiral数据集的聚类结果 (采用指数核估计) Fig. 4 The clustering results for aggregation datasets (using exponential kernel estimation) |

|
| 图 5 spiral数据集的聚类结果 (采用高斯核估计) Fig. 5 The clustering results for aggregation datasets (using gaussian kernel estimation) |
图 3(a)、3(b)所示为采用式 (4) 的指数核估计且参数dc取最小2%的距离做截断时,aggregation数据集得到的聚类决策图及相应聚类结果。由图 3(b)可知,聚类算法可以正确识别aggregation数据集的7个不同大小、形状和密度的聚类。但如果采用截断核,且令dc分别取最小5%或1%的距离做截断,聚类结果如图 3(c)、3(d)所示。图 3(c)中,聚类质量明显下降,很多样本点被误分噪声数据。由此可见,聚类结果对参数dc的取值非常敏感,进一步分析核函数选择对聚类结果的影响。定性讨论核函数及其参数dc的选择对聚类结果的影响。给定包含n个样本点的数据集D,根据式 (1),任一样本点xi∈D处的局部密度估计值dc等价于以其他样本点xj∈D为中心的、n-1个核函数的叠加,其中j≠i。这表示每个样本点的局部密度估计值等于所有其他样本点在该处的“贡献”的叠加,“贡献”的大小依赖于两点间的距离。
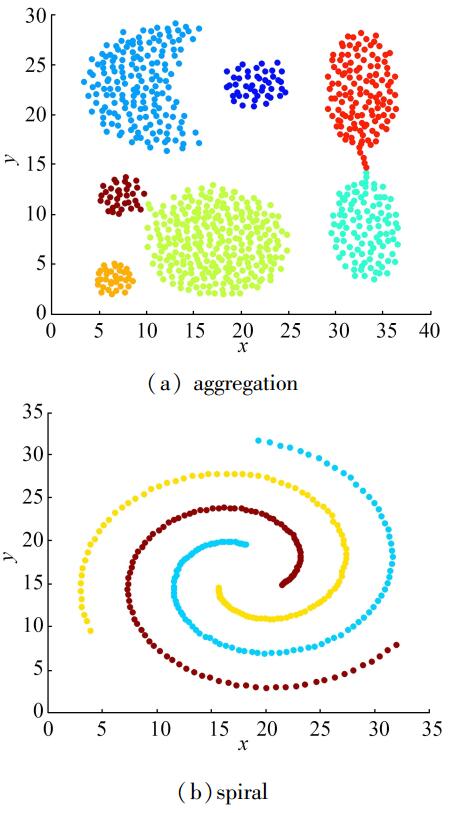
图 4(a)、4(b)所示为采用指数核估计且dc选取最小2%的距离做截断时,spiral数据集得到聚类决策图及其聚类结果,显然聚类结果可以正确识别spiral数据集的3个螺旋形聚类。但如果采用式 (5) 所示的高斯核估计,令dc分别选取最小1%或2%的距离做截断时,聚类结果如图 5(a)、5(b)所示。显然,当dc取值固定时,聚类结果对核函数的选择也非常敏感。事实上,采用高斯核估计对spiral数据集进行聚类分析,dc要选取大于2%的距离做截断,才能得到相对较好的聚类结果。而不是简单地令dc选取所有样本点间距离的最小1%-2%做截断即可。
采用式 (2) 所示的截断核估计时,每个样本点xi处的密度估计值dc为离散值,等价于xi的dc邻域内近邻样本点的个数,密度估计具有局域性。这里的密度参数dc表示截断距离,当样本点间距离超过dc时,其贡献可以忽略不计;而采用式 (3) 所示的高斯核估计时,每个样本点xi处的局部密度估计值dc为连续值,参数dc的作用也是控制密度估计的局域性,但近邻样本点的贡献会随距离的增长而衰减。根据高斯函数的数学性质,当距离大于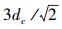
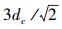
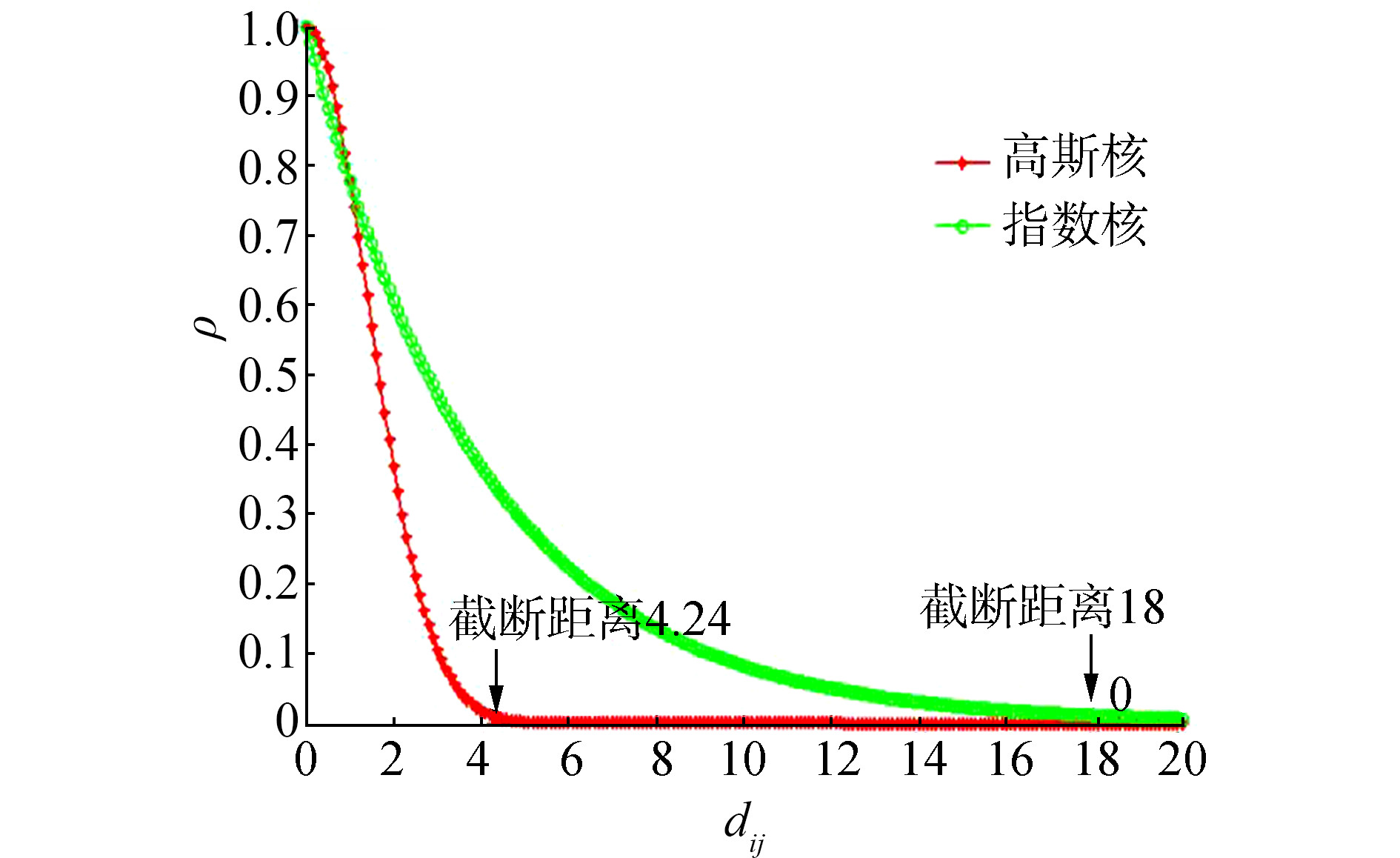
图 6所示为dc =2时指数核与高斯核的截断距离比较,图中指数核的截断距离远大于高斯核,这意味着:dc取值相同时,采用指数核估计样本点的局部密度,有贡献的近邻样本点相对更多;而采用高斯核估计进行聚类分析时,参数dc的取值应相对较大,才能产生与指数核估计相似的聚类结果。
|
| 图 6 指数核与高斯核的截断距离比较 Fig. 6 Comparison of truncative distance between exponential kernel and Gaussian kernel |
综上所述,快速搜索密度峰值点的聚类算法虽然具有良好的聚类质量,可以发现不同形状、大小和密度的聚类,可以有效处理噪声数据,但聚类结果严重依赖于核函数及其参数dc的人为选择,论文中没有讨论核函数选择对密度估计乃至最终聚类结果的影响。事实上,参数dc的选择不能脱离具体的核函数而单独讨论;即使针对特定的核函数,参数dc的取值通常也依赖于数据分布的具体特点,不存在适用于所有问题的经验策略。考虑到实际应用中,让用户选择合适的核函数及参数显然是不切实际的。下面,我们将引入一种基于密度估计熵最小化的自适应参数优化方法,根据核函数形态与底层数据分布特点自动选择合适的参数dc值,弥补核函数及其参数值人为确定的羁绊。同时,我们将引入局部密度估计值的近似计算方法改进算法性能,由此得到改进的快速搜索密度峰值点的聚类算法。
2 改进的搜索密度峰值的聚类算法 2.1 基于密度估计熵最小化的自适应参数优选信息论中用香农熵作为系统不确定性的度量,熵越大,不确定性就越大。给定n个样本点的局部密度估计值ρ1, ρ2, …, ρn,如果每个样本点的密度估计值相等,我们对底层数据分布的不确定性最大,具有最大的香农熵。反之,不确定性最小,具有最小的香农熵。由此,可以引入如下的密度估计熵[7]衡量样本点局部密度估计的合理性,即
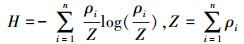 |
(6) |
式中:Z为一个标准化因子。分析密度估计熵的性质可知,有0≤H≤log (n)。显然,所有样本点的局部密度估计值近似相等时,具有最大的密度估计熵。
对于给定的核函数形态,分析密度参数dc由0至+∞递增过程中密度估计熵H的变化情况:当dc→0时,H趋近于Hmax=log (n);随着dc的增大,H首先减小,在某个优化dc值处达到最小值,然后又逐渐增大,当dc →+∞时,再次趋近于最大值Hmax=log (n)。对应最小密度估计熵的dc值可以看作参数优化值。也就是说,优化dc值可以看作一个单变量非线性函数的最优化问题,即有
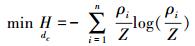 |
(7) |
此类问题存在很多标准算法,如简单试探法和模拟退火法等。实际应用中可采用样本容量的随机抽样方法降低优化dc值的时间开销。n很大时,可以采用抽样率不小于2.5%的随机抽样方法来提高优化算法的性能[5]。
理论上,对于用户任意指定的核函数形态,采用基于密度估计熵最小化的参数优化方法,都可以根据底层数据的分布特点自动优选合适的参数dc值。最终的密度估计结果取决于参数dc的优化值,而与核函数的具体形态的相关性并不明显。考虑到高斯函数具有良好的数学性质和普适性,建议采用式 (3) 所示的高斯核估计方法计算所有样本点的局部密度估计值。
2.2 局部密度估计值的近似计算给定包含n个样本点的数据集D,考虑到计算每个样本点xi∈D的局部密度估计值dc需要遍历所有其他样本点,算法复杂度较高,近似为O(n2)。根据高斯函数的数学性质,对于给定的参数dc值,当样本点间当距离大于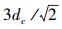
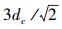
具体来说,以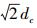
计算任一样本点xi(1≤i≤n) 的局部密度估计值ρi时,只考虑样本点xi所处网格单元cell (xi) 及其邻近网格单元neighbor (cell (xi)) 内所有样本点的影响,由此得到样本点xi的局部密度估计值ρi的近似计算公式,即有
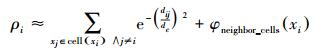 |
(8) |
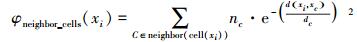 |
(9) |
其中φneighbor_cells(xi) 的计算公式代表邻近网格单元内的样本点对ρi的贡献。此时计算任一样本点的局部密度估计值所需时间开销仅为空间索引时间,即O(log (ngrid)),ngrid < < n为非空网格单元数,而构造空间索引结构所需时间为O(log (ngrid)),算法总的时间复杂度近似为O(log (ngrid))。具体算法描述如下:
2.3 改进算法描述给定数据集D={x1, x2, …, xn },改进的快速搜索密度峰值的聚类算法可以描述如下。
算法 改进的搜索密度峰值的聚类算法 (ICADEP)
输入 数据集D={x1, x2, …, xn},抽样个数nsample;
输出 数据划分Π。
算法步骤:
1) 随机抽取nsample个样本点组成抽样数据集SampleSet;
2) dc = Optimal_Parameter (SampleSet);//用抽样数据集优化估计密度参数dc;
3) Map= CreateMap (D, 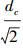
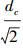
4) ρ = Density_Estimation (D, Map, dc);//计算所有样本点的局部密度估计值ρ1, ρ2, …, ρn;
5) δ = NN_Distance (D, Map, ρ );//按照局部密度估从大到小的顺序,计算所有样本点的高密度最所邻距离δ1, …, δn;
6) C=Decision_Graph (D, ρ, δ);//形成决策图,根据用户交互,确定代表聚类中心的样本子集;
7) Π=Partition (D, C);//将所有非中心样本点沿着密度估计值递增的最近邻方向,迭代划分给相应的聚类中心,实现数据划分。
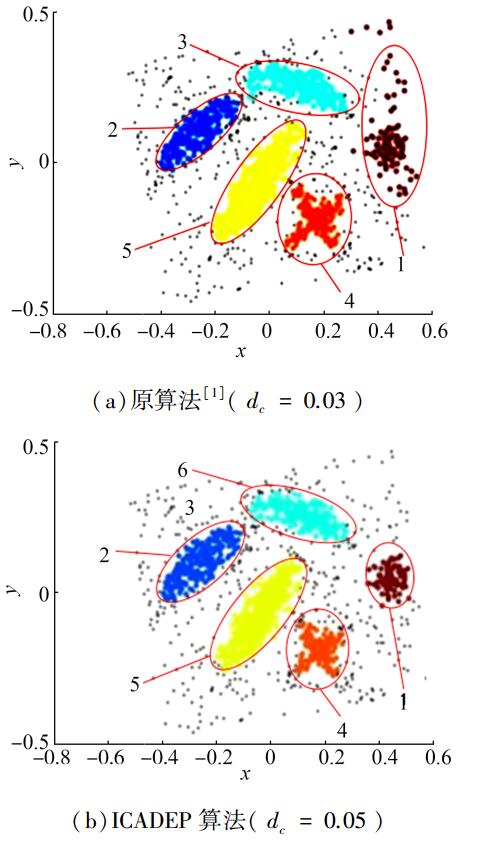
3 实验结果与比较这里采用图 1、2所示的测试数据集检验改进算法ICADEP的有效性。所有程序用软件Matlab2011实现,测试在一台PC机 (i5-3210M CPU、8GHz内存、Win7) 上进行,聚类结果如图 7~9所示。图 7所示的测试数据包含6个聚类和一些噪声数据,共4 000个样本点。图 7(a)所示为原算法[1]的聚类结果,其参数dc值是一个经验值0.03,即选取最小2%的距离做截断;图 7(b)所示为改进算法的聚类结果,其参数dc值是通过密度估计熵最小化得到的优化值,略大于论文[1]实验采用的经验值,但聚类质量相对更好,而且抗噪声能力更好。
|
| 图 7 4 000个随机样本点的聚类结果比较 Fig. 7 Comparison of clustering results of 4 000 random sample points |
|
| 图 8 aggregation数据集的聚类结果比较 Fig. 8 Comparison of clustering results for aggregation datasets |
|
| 图 9 spiral数据集的聚类结果比较 Fig. 9 Comparison of clustering results for spiral datasets |
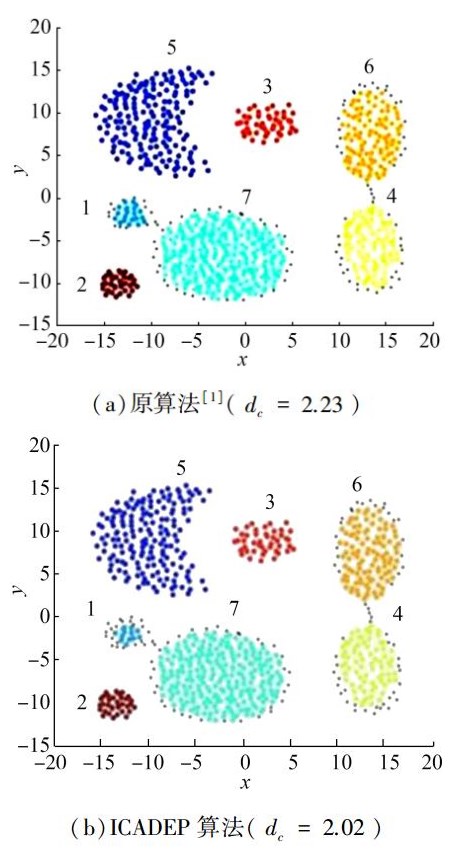
图 8(a)所示为原算法聚类结果,参数dc选取最小2%的距离做截断,即dc=2.23;而图 8(b)所示的改进算法聚类结果中,通过密度估计熵最小化得到的优化dc值虽然略小于论文[1]实验的经验值,即dc=2.02,但聚类结果同样能够正确识别原始数据分布的7个内在的数据类。
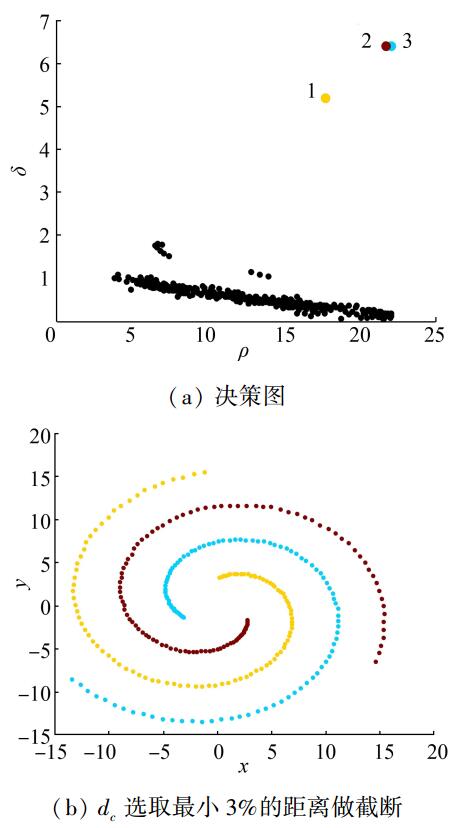
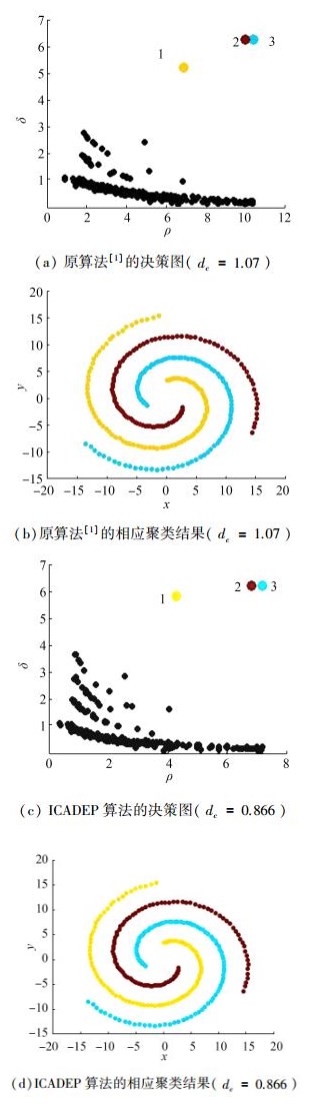
图 9所示为spiral数据集的聚类结果比较。
图 9(a)所示为原算法聚类结果,算法采用指数核估计,参数dc选取最小3%的距离做截断,即有dc=1.07;而图 9(b)所示的改进算法聚类结果中,通过密度估计熵最小化得到的优化dc值略小于论文[1]实验的经验值,即有dc=0.866,聚类结果同样能够正确识别原数据集内在的3个螺旋类。
4 结束语聚类是大数据分析与数据挖掘的基础问题。2014年刊登在《Science》上的论文《Clustering by fast search and find of density peaks》提出一种快速搜索和发现密度峰值点的聚类算法。算法简单实用,能够发现任意形状、大小和密度的聚类,能够有效处理噪声和离群数据,但聚类结果依赖于核函数及其参数dc的人为选择。论文提出一种改进的快速搜索密度峰值的聚类算法,引入基于密度估计熵最小化的自适应参数优化方法,弥补核函数及其参数值人为确定的羁绊;引入局部密度估计值的近似计算方法,改善聚类算法性能。比较实验结果表明,改进算法不仅能有效解决原算法的参数优选问题,而且具有相对更好的聚类性能,算法时间复杂度近似为O(log (ngrid)),ngrid < < n。
| [1] | RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072. |
| [2] | MANYIKA J, CHUI M, BROWN B, et al. Big data: the next frontier for innovation, competition, and productivity[M]. McKinsey Global Institute, 2011. |
| [3] | HAN Jiawei, KAMBER M, PEI Jian. Data mining: concepts and techniques[M]. 3rd ed. Burlington: Morgan Kaufmann, 2011. |
| [4] | JAIN A K. Data clustering: 50 years beyond k-means[Z]. Pattern Recognition Letters, 2009. |
| [5] | 唐杰, 东昱晓, 蒋朦, 等. SIGKDD二十周年庆典[J]. 中国计算机学会通讯, 2014, 10(10): 58-64. . |
| [6] | http://comments.sicencemag.org/content/10.1126/science.1242072 (请核对网址及补充文献内容) |
| [7] |
淦文燕, 李德毅. 基于核密度估计的层次聚类算法[J].
系统仿真学报, 2004, 16(2): 302-305.
GAN Wenyan, LI Deyi. Hierarchical clustering based on kernel density estimation[J]. Journal of System Simulation, 2004, 16(2): 302-305. |
| [8] | ESTER M, KRIEGEL H, SANDER J, et al. A density based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd international conference on knowledge discovery and data mining. Portland, 1996: 226-231. |
| [9] | GIONIS A, MANNILA H, TSAPARAS P. Clustering aggregation[J]. ACM transactions on knowledge discovery from data, 2007, 1(1): Article No.4. |



