2. 天津市智能机器人技术重点实验室, 天津 300353
2. Tianjin Key Laboratory of Intelligent Robotics, Tianjin 300353, China
近年来,随着移动机器人技术的发展,多机器人的协调控制受到了越来越多的关注。多移动机器人通过协作能完成单个机器人不能完成的任务,因此在地理勘测、巡逻侦察、安全救援和运输大型货物等领域具有广阔的应用前景。编队控制是一个典型的多机器人协调问题,是研究其他协调问题的基础,其控制算法主要包括基于行为法[1]、领航-跟随法[2-3]、虚拟结构法[4-8]和人工势场法[5]等。
移动机器人存在非完整约束和非线性特性,因此对机器人的控制更有难度。文献[6]研究了非完整移动机器人系统的一致性问题,提出了一个线性时不变连续状态反馈,使系统状态变量达到了一致。文献[7]通过坐标变换将机器人的运动模型变换成链式结构,利用反步法设计的轨迹跟踪控制器达到了期望的效果。文献[8]采用一致性算法与虚拟结构法研究了自主水下航行器小尺度编队控制问题,设计的跟踪控制律使AUV在有限时间内实现了对参考轨迹的跟踪。文献[9]将虚拟结构法和反步法相结合,提出的非线性控制算法解决了机器人编队问题,但该算法要求机器人速度不能为0。
随着多智能体协同控制理论的发展,它的控制策略已经被应用在多非完整移动机器人编队控制中。文献[10]研究了离散模型的多智能体领航跟随编队控制算法,在该算法中,通过引入基于邻居的局部控制律以及基于邻居的状态估计规则设计了一种新型控制器,经过理论分析,给出了固定拓扑和切换拓扑时系统稳定编队的充分条件。文献[11]在每个移动机器人都知道参考轨迹信息的条件下,提出了一个移动机器人编队控制器。在持续激励的条件下,文献[12-13]利用非自治系统的级联控制方法和线性智能体的协同控制方法,将非完整约束多个体系统的控制问题转化为多个线性时变系统的控制问题,文中的控制律可以实现系统K-指数稳定的跟踪控制。文献[14]提出了一种新坐标变换,将移动机器人编队问题转化为状态变量实现一致的问题,设计的分布式控制律可以使系统指数收敛于期望轨迹,但是每个机器人个体都要知道参考轨迹的角速度。
在上述工作的基础上,本文进一步研究了非完整移动机器人编队控制问题。文中通过引入坐标变换公式,将机器人编队问题转化为一致性问题。在持续激励条件下,利用邻居信息设计了分布式控制协议,然后用图论和Lyapunov方法,在理论上证明了该控制协议的正确性。最后,文中通过MATLAB仿真来验证该控制算法的可行性。不同于文献[12, 14],本文把参考轨迹视为虚拟领导者,它的状态信息只有部分跟随者能接收到。与文献[11]相比,考虑机器人之间只能进行局部信息交互,利用图论和Lyapunov方法设计的分布式控制律,可以保证整个机器人队伍指数收敛于指定队形,并且队形几何中心收敛到参考轨迹。
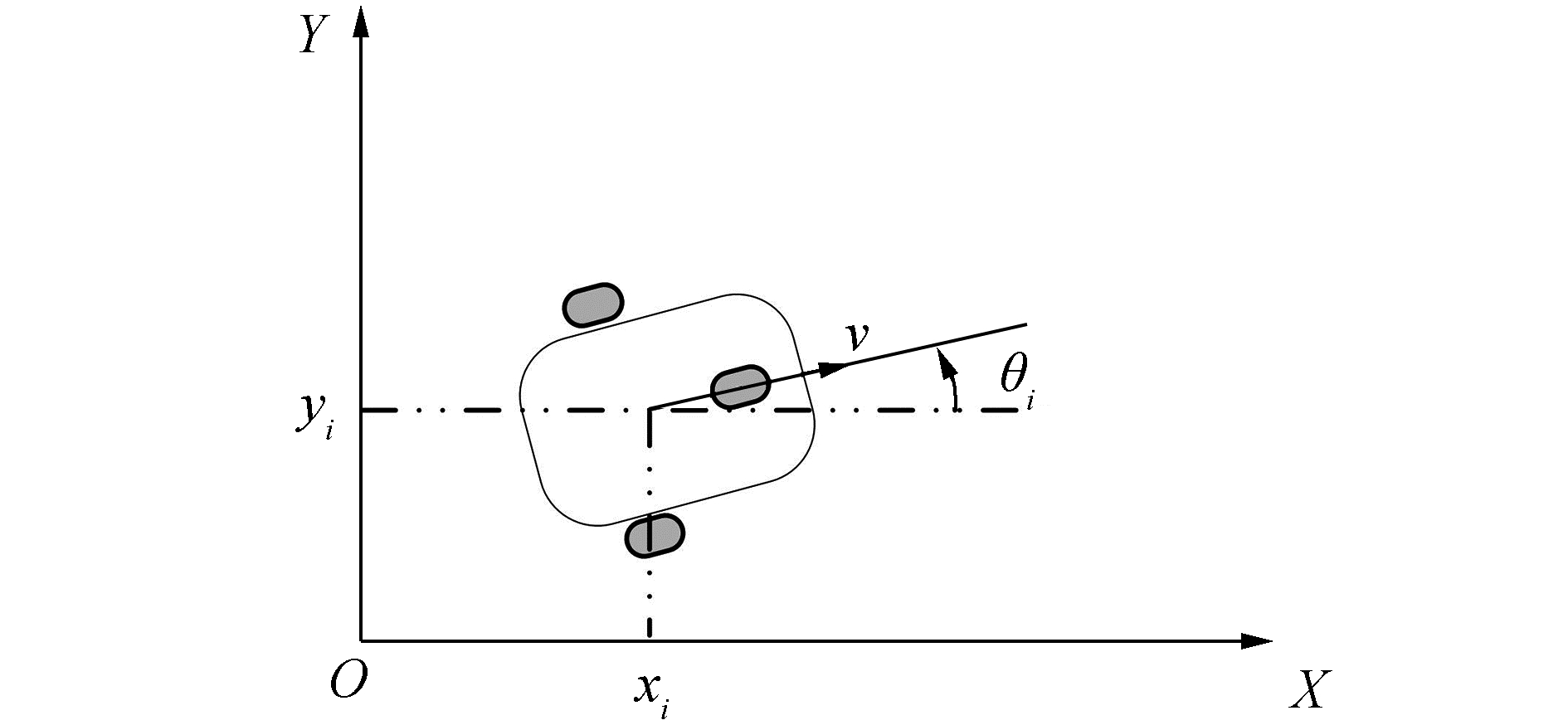
1 问题的提出考虑n个非完整约束移动机器人组成的系统,系统中的每个机器人具有相同的结构,有两个驱动轮和一个自由轮,如图 1所示。用θ={1, 2, …, n}表示移动机器人序列,移动机器人i的运动学表达式为
|
| 图 1 移动机器人示意图 Fig. 1 The sketch of mobile robot |
 |
(1) |
式中:xi, yi分别表示移动机器人i的笛卡尔坐标;θi为其航向角,即前进方向与X轴夹角;vi, ωi分别为移动机器人i的线速度和角速度。文中假设非完整约束移动机器人i满足纯滚动无滑动,用公式表示为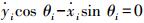
图论可以清晰完整地模拟移动机器人之间的连接关系,本文利用无向图来描述多移动机器人之间的通信关系。令G=(V, E) 表示一个无向图,V= {v1, v2, …, vn}表示由n个节点构成的节点集,E V×V表示边的集合。如果 (vi, vj)∈E,则表示机器人i与机器人j可以接收到彼此的信息。
无向图G的邻接矩阵为A=[aij]∈ Rn×n,其中aij表示 (vi, vj) 连接权重,即
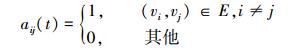 |
在无向图中,(vi, vj)∈E,则 (vj, vi)∈E,且aij=aji, i≠j。如果 (vi, vj)∈E,那么vj是vi的邻居顶点。我们定义顶点vi的邻居点集合为Ni={j∈V:(vi, vj)∈E, i≠j}。
无向图G的度矩阵为D=diag (d1, d2, …, dn),那么图G的拉普拉斯 (Laplacian) 矩阵为L=D-A。
假设n个移动机器人形成编队队形
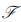

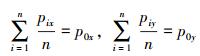 |
(2) |
为了计算简单,不失一般性,我们假设p0x=0,p0y=0。
整个机器人队伍的参考轨迹T的运动学模型为
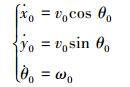 |
(3) |
式中:v0、ω0为已知时变函数。在实际应用中,机器人群体完成特定任务时,只有一个或者几个移动机器人知道任务的信息,其他机器人个体需要通过与邻居的信息交互,才能完成特定的任务。因此为了符合实际,本文将参考轨迹T视为虚拟领导者0的运动轨迹,假设参考轨迹的信息并不是全局已知的,采用牵制控制的思想,来实现多机器人编队控制。移动机器人i与虚拟领导者0之间的通信关系用对角矩阵B=diag (b1, b2, …, bn) 来表示。如果机器人i能获得虚拟领导者0的信息,则对角元素bi=1,否则bi=0。
分布式编队控制的目标是基于邻居和自己的状态信息,为每个机器人设计控制器,使整个机器人队伍形成编队队形
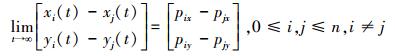 |
(4) |
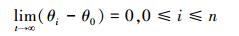 |
(5) |
 |
(6) |
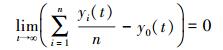 |
(7) |
在介绍分布式控制算法之前,先给出本文的一些符号表示和多机器人系统满足的两个假设,以及后面证明所需要用到的两个重要引理。
本文约定如下:I代表单位矩阵;1n=[1 1 … 1]T∈Rn;λmin(·) 和λmax(·) 分别表示矩阵的最小特征值和最大特征值;向量x的2-范数为‖
x‖2,1-范数为‖x‖1;矩阵A的F-范数为‖A‖F;当x=[x1 x2 … xn]T, sign (x)=[sign (x1) … sign (xn)]T,其中,当xi≠0时,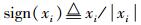
假设1[12-13] ω0是持续激励信号,即存在正常数α1、α2和δ,使得对于所有的t>0,满足
 |
假设2 图G是无向连通的,至少存在一个移动机器人和虚拟领导者0是直接连通的,且这种连通是单向的。
引理1[15] 如果实数矩阵A∈Rn×n正定对称,那么对于任意向量x∈Rn都满足下面条件
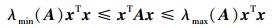 |
引理2[16] 对于矩阵B=diag (b1, b2, …, bn)>0,如果无向图G连通,那么矩阵L+B是正定的。
2 分布式控制算法 2.1 控制器的设计为了便于控制器的设计,我们将移动机器人的运动学模型进行坐标变换,使用如下的坐标变换[13]:
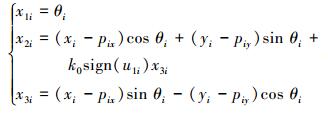 |
(8) |
同时,控制输入的变换方程为
 |
(9) |
通过上述变换,机器人i运动学模型变为
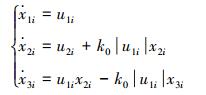 |
(10) |
式中:0≤i≤n;k0>0;x1i, x2i, x3i表示系统坐标变换后的状态量;u1i, u2i表示系统坐标变换后控制输入。
通过上面的坐标变换式 (8),多移动机器人编队问题转化为新状态变量x1i, x2i, x3i实现一致的问题。采用误差控制策略,定义变换后的状态误差为
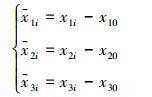 |
(11) |
对式 (11) 求导可得
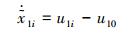 |
(12) |
 |
(13) |
 |
(14) |
为了解决多机器人编队问题,把状态误差系统式 (12)~(14) 分解为一个一阶子系统和一个二阶子系统,其中一阶子系统的运动学方程为式 (12),二阶子系统的运动学方程为式 (13) 和式 (14)。考虑只有部分机器人与虚拟领导者0有信息交互,设计u1i,使得一阶子系统式 (12) 在有限时间内收敛于0;设计u2i,使得二阶子系统式 (13) 和式 (14) 指数收敛于0。构造如下的分布式控制律:
 |
(15) |
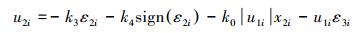 |
(16) |
式中:

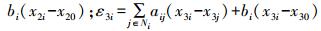
根据控制律式 (15) 和式 (16),以机器人1为例,控制算法的原理框图如图 2所示。它由两部分组成,一部分为机器人坐标变换i∈θ,另一部分为分布式控制器。

|
| 图 2 移动机器人1控制原理框图 Fig. 2 The control principle block diagram of mobile robot 1 |
对于一阶子系统式 (12),考虑分布式控制律式 (15),将式 (10) 中
 |
(17) |
令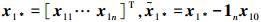
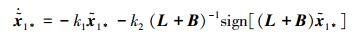 |
(18) |
定理1 系统满足假设1和假设2,则分布式控制律式 (15) 能使系统式 (18) 在有限时间内收敛于0,即
 |
式中,
证明 针对系统式 (18),构造如下的Lyapunov函数:
 |
根据引理1,可得到
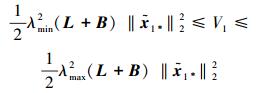 |
对V1求导可得
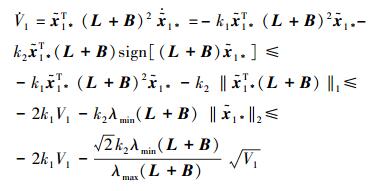 |
求解上述微分不等式可得:当0≤t≤T1时,
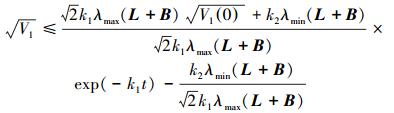 |
当t≥T1时,V1(x)=0。因为L+B>0,由V1和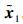
收敛时间T1依赖于初始值V1(0),满足下式:
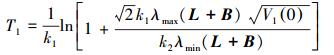 |
定理1证毕。
从定理1中u1i的收敛时间T1表达式可以看出,k2影响一阶子系统的收敛速度,k2越大,收敛速度越快。但是k2越大,由于sign (·) 函数不连续所造成的抖振现象对系统稳定性影响越大,所以,选择k2时,需要综合考虑控制精度、收敛速度等方面影响。二阶子系统表达式 (13) 和式 (14) 中存在变量u1i,所以一阶子系统的动态特性会影响二阶子系统的动态特性,但是一阶子系统式 (12) 稳定性并不受二阶子系统中变量的影响。由定理1可知,在控制律式 (15) 的作用下,x1i, u1i在有限时间T1内收敛于x10, u10。所以下面我们只考虑二阶子系统式 (13) 和式 (14)。
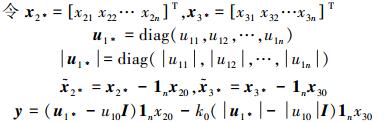 |
基于分布式控制协议式 (16),二阶子系统式 (13) 和式 (14) 闭环特性可以表示为下面的矩阵形式:
 |
(19) |
定理2 系统满足假设1和假设2,则控制律式 (18) 能使式 (19) 描述的二阶子系统指数收敛于0,即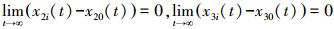
证明 由定理1可知,当t>T1时,u1i(1≤i≤n) 收敛到u10,下面分两步来证明定理2。
1) 证明当t≤T1时,

对闭环系统式 (19) 构造的Lyapunov函数为
 |
(20) |
根据引理1可以得到
 |
(21) |
式中,α=min (λmin(L+B), λmin2(L+B))。
对V2沿着轨迹式 (19) 求导可得
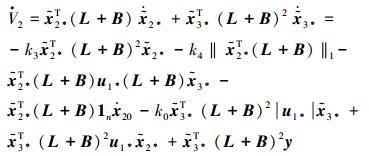 |
(22) |
根据定理1可知,在有限时间内,机器人的状态误差

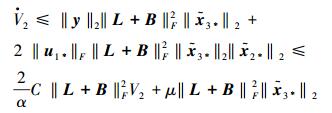 |
当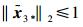
 |
(23) |
当
 |
(24) |
结合式 (23) 和式 (24) 可知,对于任何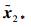
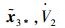
 |
求解上述微分不等式可得
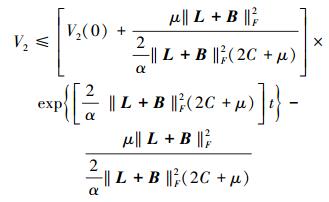 |
于是,当t≤T1时V2是有界的,进而
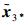
2) 证明当t>T1时,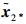
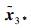
根据定理1,当t>T1时,u1i=u10,x1i=x10,则二阶子系统闭环表达式 (19) 化简为
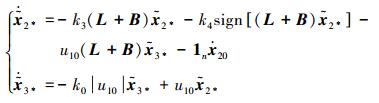 |
(25) |
则式 (22) 整理为
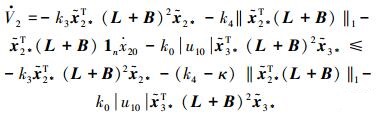 |
(26) |
因为式 (26) 中 (L+B)2>0,k4>κ,k3>0,所以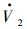
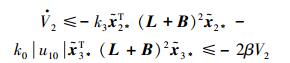 |
式中β=min (k3λmin(L+B), k0|u10|)。那么,可得V2≤ 

综合定理1和定理2,当t≤T1时,一阶子系统的变量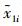
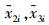



本节中,我们用MATLAB对移动机器人系统进行了仿真研究,仿真中n=4,移动机器人之间的通信拓扑为
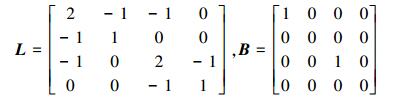 |
期望的编队队形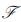
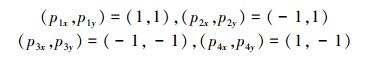 |
虚拟领导者0的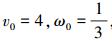
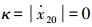
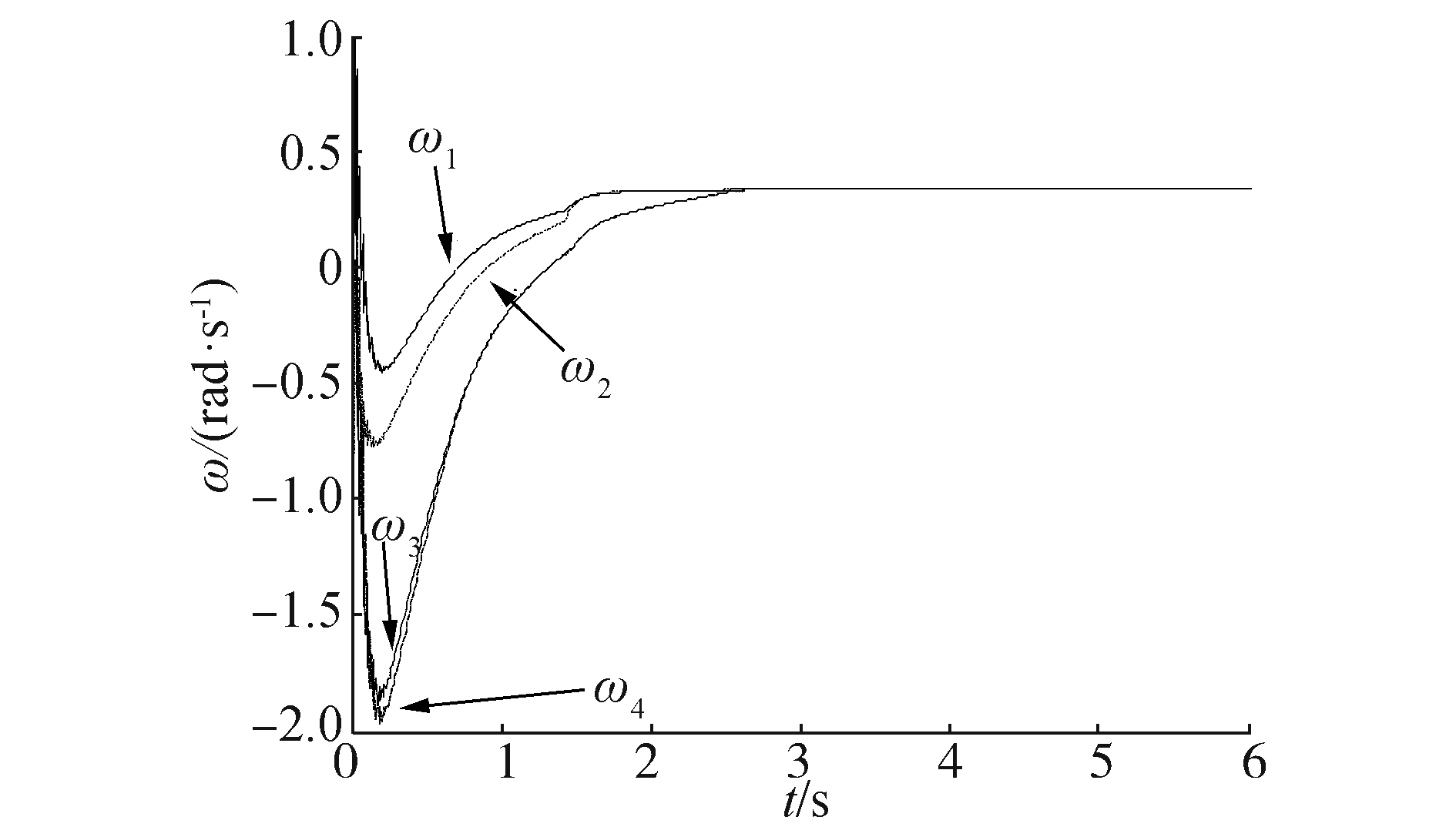
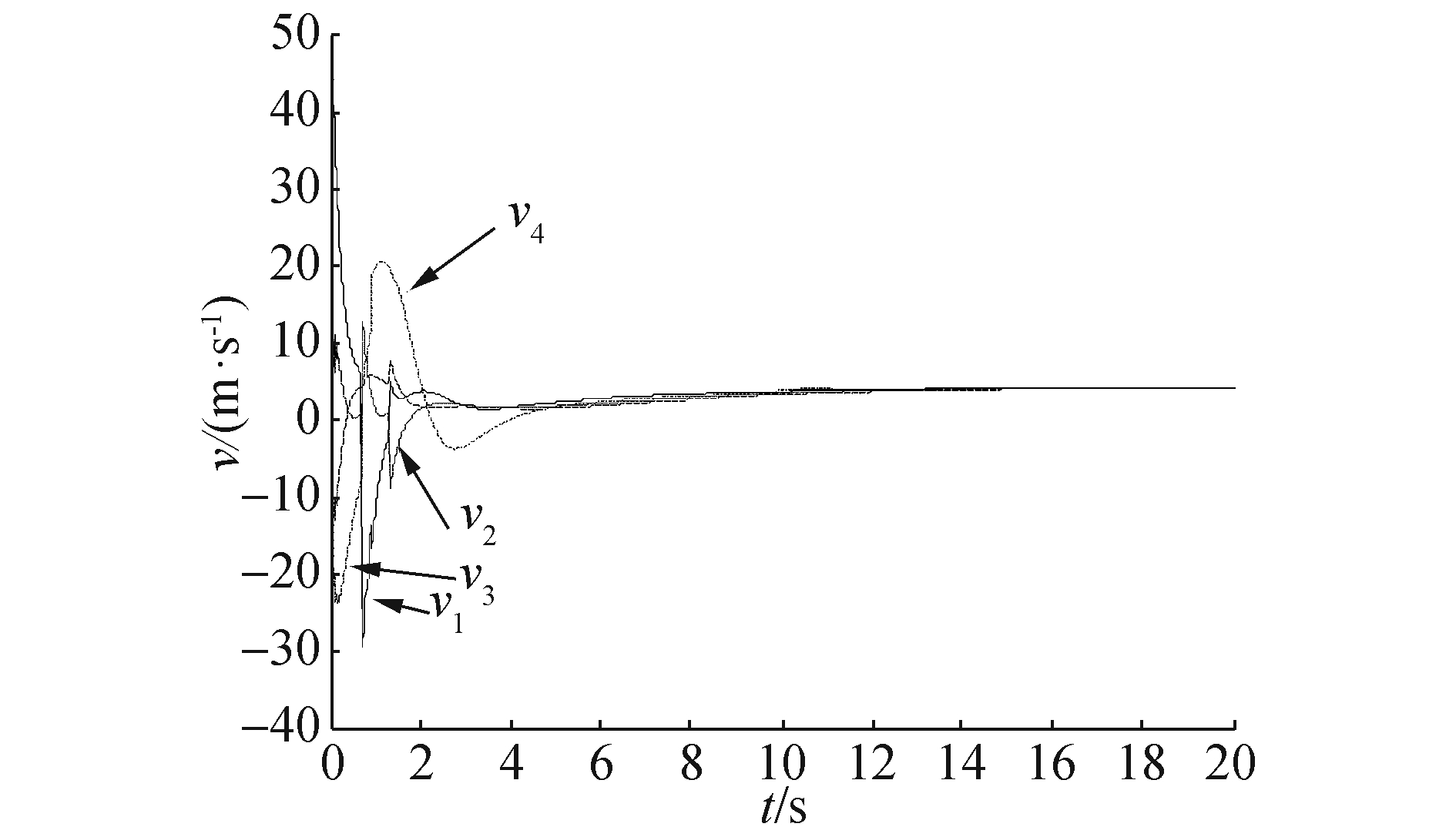
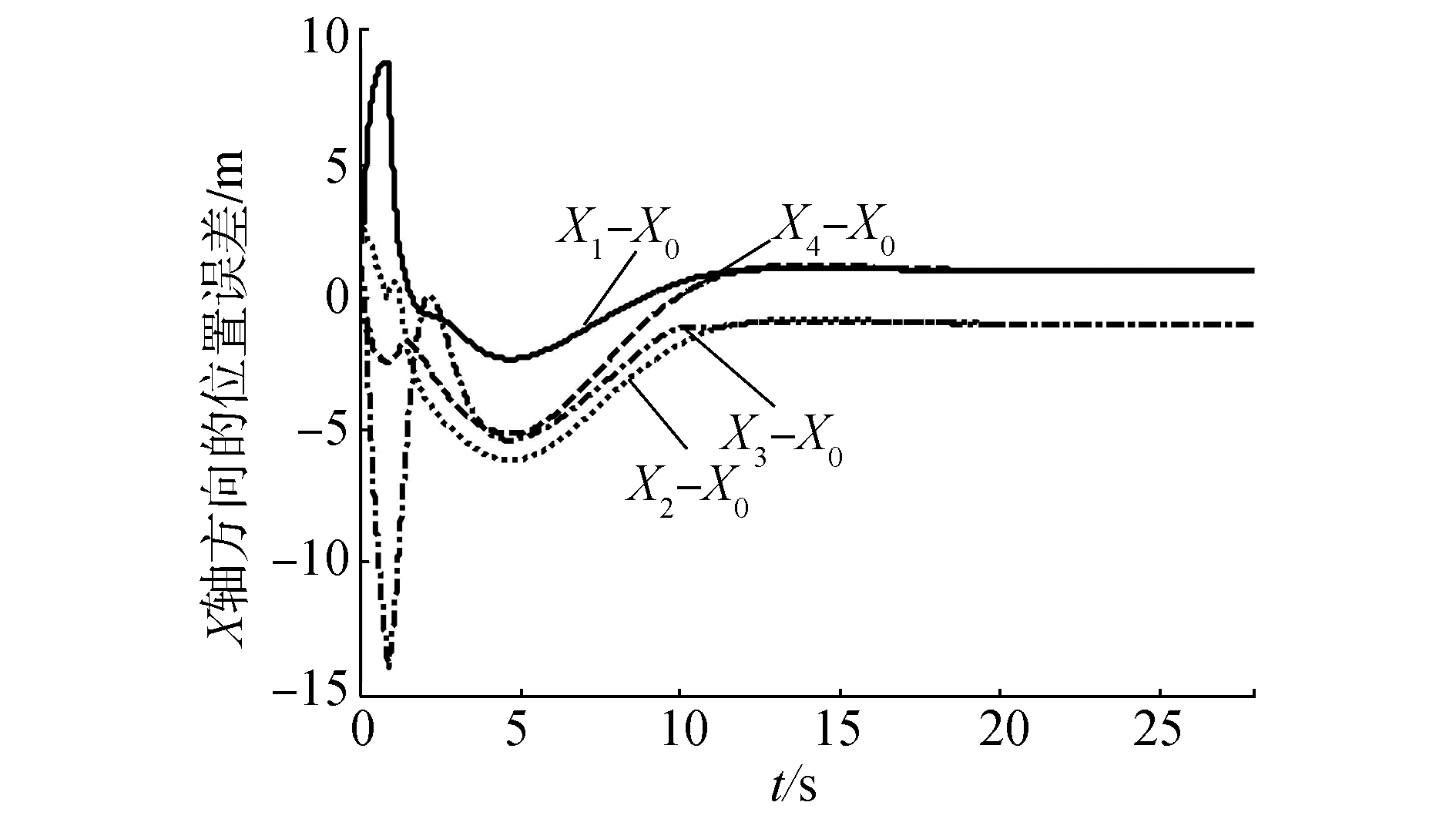
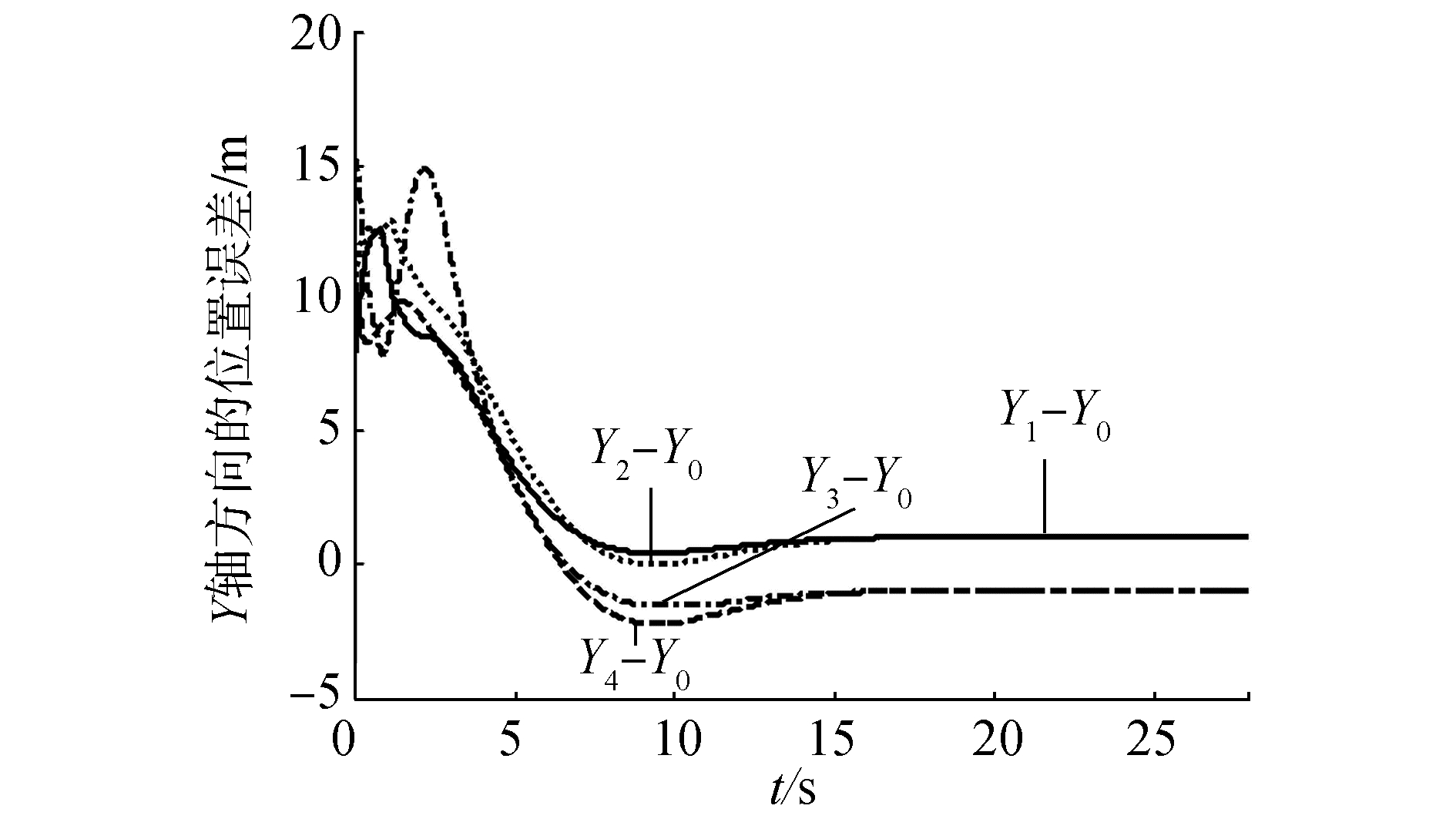
在图 3中,每个四边形中的4个*表示4个跟随者,实线和虚线分别表示虚拟机器人0和编队几何中心的运动轨迹,从图中可以看出4个跟随者形成了指定正方形编队,同时编队队形的几何中心收敛到虚拟领导者0的运动轨迹。图 4和图 5分别给出了3个跟随者的控制输入ωi, vi(i=1, 2, 3, 4),从图中可以看出,在15 s之后,ωi, vi收敛到ω0, v0。图 6~8分别表示4个跟随者与虚拟机器人0的航角和位置之间的误差。在20 s后,4个跟随者与虚拟领导者0之间的航角误差为0,x轴和y轴方向的位置误差分别为pix和piy(i=1, 2, 3, 4)。从上述仿真实验可以看出,所设计的控制器可以使移动机器人形成期望的编队。

|
| 图 3 移动机器人编队运动轨迹 Fig. 3 Trajectory of tracking of mobile robots formation |
|
| 图 4 移动机器人控制输入ω Fig. 4 The control input ω of the mobile robots |
|
| 图 5 移动机器人控制输入v Fig. 5 control input v of the mobile robots |

|
| 图 6 航角误差θe Fig. 6 Heading errors θe |
|
| 图 7 X轴方向的位置误差xe Fig. 7 Position errors in X coordinates |
|
| 图 8 Y轴方向的位置误差ye Fig. 8 Position errors in Y coordinates |
本文以多非完整移动机器人为研究对象,通过坐标变换将编队问题转化为移动机器人状态量的一致性问题。在持续激励信号作用下,利用邻居状态信息设计了分布式控制协议,然后用图论和Lyapunov方法,在理论上证明了该控制协议可以很好地解决机器人编队问题。最后,通过MATLAB对该控制算法进行了验证。从仿真实验结果可以看出,本文提出的控制算法可靠性好,能在较短时间内顺利形成编队。本文假设通信拓扑结构是无向连通的,但在实际应用中,系统之间的通信网络往往是有向的或者存在时滞,所以,将来的研究工作将围绕着有向通信拓扑来开展。
| [1] | BALCH T, ARKIN R C. Behavior-based formation control for multirobot teams[J]. IEEE transactions on robotics and automation, 1998, 14(6): 926-939. DOI:10.1109/70.736776. |
| [2] | SHAO J, XIE G M, WANG L. Leader-following formation control of multiple mobile vehicles[J]. IET control theory & applications, 2007, 1(2): 545-552. |
| [3] | DESAI J P, OSTROWSKI J P, KUMAR V. Modeling and control of formations of nonholonomic mobile robots[J]. IEEE transactions on robotics and automation, 2001, 17(6): 905-908. DOI:10.1109/70.976023. |
| [4] | TAN K H, LEWIS M A. Virtual structures for high-precision cooperative mobile robotic control[C]//Proceedings of the 1996 IEEE/RSJ International Conference Intelligent Robots and Systems'96. Osaka, Japan, 1996: 132-139. |
| [5] | KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. International journal of robotics research, 1986, 5(1): 90-98. DOI:10.1177/027836498600500106. |
| [6] | ZHAI G, TAKEDA J, IMAE J, et al. Towards consensus in networked non-holonomic systems[J]. IET control theory & applications, 2010, 4(10): 2212-2218. |
| [7] | YUAN Z P, WANG Z P, CHEN Q J. Trajectory tracking control of a nonholonomic mobile robot[C]//Proceedings of the 8th IEEE International Conference on Control and Automation. Xiamen, China, 2010: 2207-2211. |
| [8] |
袁健, 唐功友. 采用一致性算法与虚拟结构的多自主水下航行器编队控制[J].
智能系统学报, 2011, 6 (3): 248-253.
YUAN Jian, TANG Gongyou. Formation control of autonomous underwater vehicles with consensus algorithms and virtual structure[J]. CAAI transactions on intelligent systems, 2011, 6(3): 248-253. |
| [9] | CHEN Lei, MA Baoli. A nonlinear formation control of wheeled mobile robots with virtual structure approach[C]//Proceedings of the 34th Chinese Control Conference. Hangzhou, China, 2015: 1080-1085. |
| [10] |
王中林, 刘忠信, 陈增强, 等. 一种多智能体领航跟随编队新型控制器的设计[J].
智能系统学报, 2014, 9 (3): 298-306.
WANG Zhonglin, LIU Zhongxin, CHEN Zengqiang, et al. A kind of new type controller for multi-agent leader-follower formation[J]. CAAI transactions on intelligent systems, 2014, 9(3): 298-306. |
| [11] | DONG Wenjie, FARRELL J A. Decentralized cooperative control of multiple nonholonomic dynamic systems with uncertainty[J]. Automatica, 2009, 45(3): 706-710. DOI:10.1016/j.automatica.2008.09.015. |
| [12] | CAO Kecai, YANG Hao, JIANG Bin. Formation tracking control of nonholonomic chained form systems[C]//Proceedings of the 10th IEEE International Conference on Control and Automation (ICCA). Hangzhou, China, 2013: 846-851. |
| [13] | CAO Kecai, JIANG Bin, CHEN Yangquan. Cooperative control design for non-holonomic chained-form systems[J]. International journal of systems science, 2015, 46(9): 1525-1539. DOI:10.1080/00207721.2013.809615. |
| [14] | PENG Zhaoxia, WEN Guoguang, Rahmani A, et al. Distributed consensus-based formation control for multiple nonholonomic mobile robots with a specified reference trajectory[J]. International journal of systems science, 2015, 46(8): 1447-1457. |
| [15] | 方勇纯, 卢桂章. 非线性系统理论[M]. 北京: 清华大学出版社, 2009: 1-151. |
| [16] | HONG Yiguang, HU Jiangping, GAO Linxin. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177-1182. DOI:10.1016/j.automatica.2006.02.013. |



