大多数传统的聚类算法仅仅能得到单个结果,但是当对复杂数据进行聚类分析时,很可能存在多个具有合理性的聚类结果。这一特点在高维数据上表现得尤为明显,例如文本、图像、基因数据等,这些数据具有多种特征,而不同的特征子空间往往会得到完全不同的聚类结果,同时每一种结果都能体现数据不同的结构信息。
本文根据文献[1]所述原理,提出了一种能够发掘多个可供选择的聚类结果的算法RLPP。算法结合了希尔伯特施密特独立性度量准则(hilbert-schmidt independence criterion,HSIC)[2]以及局部保持投影(locality preserving projections,LPP)[3],改进了LPP算法学习子空间的过程。由于HSIC可以高效地评估不同随机变量之间的依赖性,而LPP算法具有流形学习能力,因此RLPP同时兼顾了聚类结果的相异性和聚类质量这两大要素。并且由于其目标函数最终在特征分解问题的框架内求解,因此能够确保求出的新的子空间一定存在,并且解是全局最优的。
总的来说,本文所做的工作为:1)提出了一种新的算法RLPP,用于发掘多种可供选择的聚类结果;2)RLPP根据同时满足质量和相异性要求的目标函数,生成一个新的特征子空间,该特征子空间能够确保存在,并且是全局最优的;3)通过实验,验证了RLPP的效果,并与其他现有的算法进行了性能比较。
1 当前典型的可选聚类发掘方法当前,有关发掘可选聚类结果的算法大体上可以分为两类:一类直接利用原始数据空间寻找,另一类则是基于投影(变形)子空间寻找。
1.1 基于全部原始数据空间这类研究利用的是整个原始特征空间,大多数研究的不同之处在于优化聚类质量和相异性的目标函数不同。文献[4-9]中的研究可以归类为此类。文献[4]提出了一种分层聚类(hierarchical clustering)算法COALA,该算法把从提供的聚类结果中生成的cannot-link约束项合并入它的每一个凝聚步骤中,即尽可能多地满足这些cannot-link约束项。在文献[7]中,提出了CAMI算法,用于同时寻找两个可供选择的聚类结果。CAMI算法在混合模型下构造聚类问题,优化了一个双重目标函数(dual-objective function),使得当两个混合模型之间的互信息(反映了两种聚类结果之间的不同)最小时,对数似然(反映了聚类质量)最大。文献[6]提出的两种算法Dec-kmeans和Conv-EM也属于此类,这两种算法分别改进了k-means和EM的目标函数,结合了一个修正项,用于表示两种聚类结果之间的去相关信息。文献[8]中的工作采用了不同的方式,其原理来源于信息论,它的目标函数最大化全部数据实例和可选聚类结果类标之间的互信息(MI),同时最小化可选聚类和所提供的聚类结果之间的互信息。文献[8]中并没有基于传统的香农熵[10],而是采用了Renyi熵,以及相对应的二次互信息[11-12],这种方法在结合了非参数Parzen窗[13]后使得MI基本近似。这种双重优化聚类目标同样被用于文献[9]中,区别在于文献[9]使用的是迭代法,而不是文献[8]中所使用的分层技术。
1.2 基于投影子空间如果原数据空间的子空间与原数据空间是相互独立的(比如是正交的),那么根据该子空间得到的聚类结果也与原聚类结果不同。文献[14-18]就是根据这样的理论基础提出了各自的算法。文献[14]由正交投影方法提出了两种寻找可供选择的聚类结果的算法。已知一个向量b,投影到矩阵的列空间中,可以用P×b计算,其中P被称为投影矩阵,P=A(ATA)-1AT。而(Ⅰ-P)同样也是一个投影矩阵,表示把投影到了AT的零空间中。文献[14]中提出的2种算法把每个数据实例看作向量,利用了上述投影等式。文献[15]中的研究也与此相关,投影矩阵被应用于从所提供的聚类结果导出的距离矩阵上。相比于文献[14]中的2种算法,这种方法的优势在于能够解决数据维数比类别数小的情况。文献[16]提出的算法采用了不同的方法,通过对数据的投影,使得在参考聚类结果中属于相同类别的数据点经过映射后在新的空间中拉开距离。这一方法与其他方法之间的不同之处在于它并不寻找一个全新的可选聚类,而是通过设定2个聚类结果之间的相异度阈值,允许已知的聚类结果中的部分在可选聚类结果中保留下来。文献[17]和文献[18]中所提出的算法基于谱聚类实现,前者表明可选聚类结果可以通过拉普拉斯矩阵不同的特征向量找到,后者所提出的多重谱聚类(multiple spectral clustering,MSC)把子空间学习技术融入了谱聚类的过程中,也就是说,MSC的目标函数是一个对偶函数(dual-function),通过最优化一项来修正另一项。另外,文献[1]提出了正则化PCA(regularized PCA,RPCA)和正则化的图方法(regularized graph-based method,RegGB)算法,其中RPCA与MSC一样,都采用了HSIC,用于评估相关性,而RegGB算法则是基于图论构造。总的来说,RPCA和RegGB算法在寻找可选聚类的能力上要优于之前所提到的算法,但是RPCA算法只适用于线性结构的数据集,并且其寻找可选聚类结果的能力有限,往往只能找到一个可选聚类,这些都极大地影响了它在使用上的灵活性。因此,本文在文献[1]所提出的思路上,探索了一种新的算法,通过引入流形学习大大提高了其发掘低维流形结构的能力和子空间学习能力,并通过核化扩大了其适用范围,使得其既适用于线性,同时又适用于非线性的数据集。
2 问题描述假设数据集X={x1 x2 … xn},xi∈Rd,即X是d×n的矩阵,并提供一个使用任意聚类算法得到的参考聚类结果C(1)。则本文研究的目标为:发掘数据集X上的可供选择的聚类结果C(2),并且C(2)中的所有类别Ci(2)必须满足两个条件,UiCi(2)=X和Ci(2)∩Cj(2)=Ø(∀i≠j)。除了与C(1)不同外,还要求C(2)的聚类质量较高。同理,若提供一组参考聚类结果{C(1),C(2),…},必须生成高质量的可供选择的聚类结果C(k),且与之前所有的聚类结果{C(1),C(2),…}不同。
为了发掘另一个可供选择的聚类结果,使用子空间流形学习方法,将原始数据空间X映射到一个新的子空间中。该空间保留了X的特征,并且完全独立于其他的参考聚类结果。任何聚类算法都可以使用这个新的子空间进行聚类分析。
3 局部保持投影局部保持投影(locality preserving projections,LPP)[3]是一种非监督降维方法,是流形学习算法Laplacian Eigenmap的线性逼近。给定Rd中的n个数据点x1,x2,…,xn,LPP通过寻找转换矩阵A,将这n个数据点映射为Rl(l<<d)上的数据点y1,y2,…,yn,即:
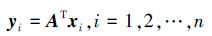 |
(1) |
式中所需的转换矩阵A可以通过最小化式(2)目标函数得到:
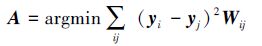 |
(2) |
式中:Wij是权值矩阵,可采用k最近邻算法得到邻接图,再求出权值矩阵。
如果xj是xi的k近邻点,则
从目标函数式(2)可以看出,降维后的特征空间可以保持原始高维空间的局部结构。结合式(1)和式(2),做简单的代数变换:
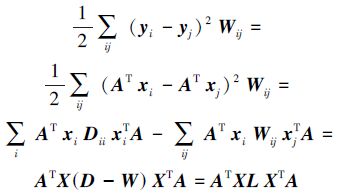 |
(3) |
式中:X=[x1 x2 … xn],D是一个n×n的对角矩阵,对角线元素Dii=$\sum\limits_{j}{{}}$Wij,L是拉普拉斯矩阵,L=D-W。
能够使得式(3)取最小值的变换矩阵A的求解可以转换为如下的广义特征值问题:
 |
(4) |
将式(4)求解出的特征值按从小到大排列,即λ0<…<λl-1,取前k个最小的特征值对应的特征向量a0,a1,…,ak-1组成A,即A=[a0 a1 … ak-1],由于ai是列向量,所以A是d×k的矩阵。
此外,LPP不仅适用于原始数据空间,还适用于再生核希尔伯特空间(reproducing kernel hilbert space,RKHS),这样就可以引出核LPP算法。
假设欧式空间Rn中的数据矩阵通过非线性映射函数φ映射到希尔伯特空间K,即φ:Rn→K。使用φ(X)表示希尔伯特空间中的数据矩阵,即φ(X)=φ(x1)φ(x2) …φ(xn)。那么,在希尔伯特空间中的特征向量问题就可以表示为
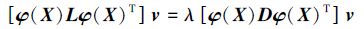 |
(5) |
考虑如下的核函数:
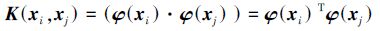 |
式(5)中的特征向量是φ(
x1),φ(x2),…,φ(xn)的线性组合,每一项的系数分别为ai,i=1,2,…,m,即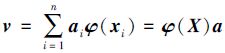
已知一个参考聚类结果C(1),使用RLPP算法学习相对于C(1)独立的子空间A,这样就确保了使用A得到的聚类结果C(2)与C(1)不同。为了计算不同子空间之间的相异性,采用了HSIC(hilbert-schmidt independence criterion)[1],更重要的是,LPP与HSIC结合后可以导出一个特征分解问题,这样就一定可以计算出全局最佳解。
HSIC是一种基于核的独立性度量方法,采用Hilbert-Schmidt互协方差算子,通过对该算子范数的经验估计得到独立性判断准则。具体来说,已知X和Y两个随机变量,HSIC(X,Y)的值越大说明X和Y的关联性越强,值等于0时说明X和Y相互之间完全独立。
数学上,令F表示再生核希尔伯特空间,φ(x)表示数据x从原空间映射到F中的映射函数,则核函数可以写为K(x,xT)=〈φ(x),φ(xT)〉。同样的,定义ψ(y)为原空间中的数据y映射到再生希尔伯特空间G的映射函数,核函数可以写为L(y,yT)=〈ψ(y),ψ(yT)〉。则互协方差算子Cxy:G→F可以被定义为Cxy=Exy(φ(x)-μx)⊗(ψ(y)-μy),⊗表示张量积。Cxy即为Hilbert-Schmidt算子,而HSIC定义为Cxy的Hilbert-Schmidt算子范数,即HSIC(Pxy,F,G)=‖Cxy‖HS2,其中Pxy表示X和Y的联合分布。实际上,不需要知道联合分布Pxy,已知n个观测值Z=(x1,y1),…,(xn,yn),可以直接给出HSIC的经验估计值为HSIC(Z,F,G)=(n-1)-2tr(KHLyH)。其中K,Ly∈Rn×n,且K,Ly分别是核K和L关于Z观测值的Gram矩阵,即Kij=k(xi,xj),Lyij=l(yi,yj)=〈yi,yj〉,其中yi是一个二元向量,表示对xi的类标签所做的编码(稍后将举例说明)。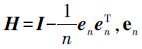
为了表示简单,使用HSIC(X,Y)代替HSIC(Z,F,G),表示随机变量X和φ(x)=ATx,也就是X和Y之间的依赖性。
假设有8个数据{x1,x2,…,x8,},其中x1和x2,x3和x4,x5和x6,x7和x8分别为一类。则向量y1=y2=(1 0 0 0)T,y3=y4=(0 1 0 0)T,y5=y6=(0 0 1 0)T,y7=y8=(0 0 0 1)T。矩阵Y的每一行对应一个yi。Ly是一个8×8的矩阵,由yi和yj的点积构成。K是一个8×8的矩阵,表示φ(xi)和φ(xj)之间的相似度。同时注意,根据定义, H是一个n×n(在本例中是8×8)的常数矩阵,每行每列的和都等于0。因此,在上述示例中,每一行(列)都包含7个(-1/8)和1个7/8。
5 基于局部保留投影的多可选聚类发掘算法由于通过HSIC(X,Y)可以自然地评估结构很复杂的样本X和Y之间的相关性,因此结合HSIC(X,Y)对LPP的目标函数进行修改。要求是转换矩阵A必须能够发掘嵌入在高维数据中的低维流形结构,并且与已知的聚类结果C(1)完全独立。换句话说,在所有与已经存在的聚类结果C(1)不同的子空间中,要选出能够最好地保持高维数据流形结构的子空间。因此,改进LPP的目标函数如下:
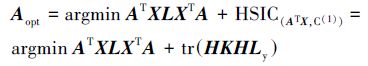 |
(6) |
式中:Aopt表示A的最佳解,且由迹的性质可知trHKHLy=trKHLyH。不同的核函数在计算变量之间的独立性时结果不同,这里采用线性核函数,映射函数定义为:
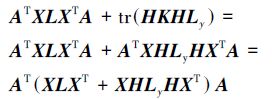 |
(7) |
将数据集合X映射到高维特征空间中后,就可以最终得到φ(X)=[φ(x1) φ(x2) … φ(xn)]。其中,核矩阵K的元素为Kij=φ(xi)T·φ(xj)。即:
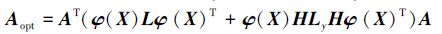 |
(8) |
因为H和Ly都是对称矩阵,所以φ(X)HLyHφ(X)T也是对称矩阵,同样,因为L是对称矩阵,所以φXLφ(X)T也是对称矩阵。因此,φ(X)Lφ(X)T+φ(X)HLyHφ(X)T是实对称矩阵。作为一个特征分解问题,Aopt的最优解由前k个最小非零特征值对应的特征向量构成,即A=[α1 α2 … αk]。下一步,可以使用k-means[19]算法对子空间A进行聚类,得到可供选择的聚类结果C(2)。
可以看到,φ(X)HLyHφ(X)T直接影响了LPP算法中φ(X)Lφ(X)T项,也就是说,可以把两个聚类结果之间的独立性看作添加的约束项。同时,通过添加更多的HSIC项,将算法推广可以找到更多可供选择的聚类结果。
举例来说,在寻找第3个可供选择的聚类结果C(3)时,只要提供之前找到的两个聚类结果C(1)和C(2),并把式(6)中的HSIC(ATX,C(1))一项替换为HSIC(ATX,C(1))+HSIC(ATX,C(2))即可。因此只要在式(8)中使用ATXHLy1HXTA+ATXHLy2HXTA,即直接使用ATXH(Ly1+Ly2)HXTA代替ATXHLyHXTA。也就是说,使用(Ly1+Ly2)代替了Ly,其他矩阵保持不变即可。
RLPP算法描述如下:
1) 输入 数据集X;
一个X上的参考聚类结果C(1)。
2) 输出 一个数据集X上可供选择的参考聚类结果C(2)。
3) 算法流程:
①计算Ly,Ly=〈yi,yj〉,其中yi是一个二元向量,表示C(1)中xi的类标签的编码。
②计算H=I-1nenenT。
③计算权值矩阵W,如果xj是xi的k近邻点,那么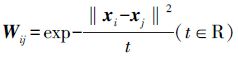
④计算矩阵D, Dii=$\sum\limits_{j}{{}}$Wij,计算拉普拉斯矩阵L,L=D-W。
⑤使用高斯核计算核矩阵K,Kij=φ(xi)T·φ(xj)。
⑥分解核矩阵K,K=PTΛP,根据φ(X)=Λ12P得到φ(X)。
⑦计算φ(X)Lφ(X)T+φ(X)HLyHφ(X)T的特征值和特征向量。
⑧按特征值从小到大的顺序对特征向量排序。
⑨选择前k个最小的特征值对应的特征向量,即A=[a0 a1 … ak-1]。
⑩C(2)=k-means(ATφ(X))。
RLPP算法的时间复杂度完全由计算最近邻矩阵以及核矩阵决定,因为它们的时间复杂度均为O(n2d),因此整体的时间复杂度也为O(n2d)。
6 实验与分析 6.1 聚类结果评估聚类结果根据聚类质量和相异性两方面进行评估。聚类质量分为两种情况:如果已知正确的类标,则可选聚类结果和正确的类标之间通过F-measure计算,计算公式为F=2P×R/(P+R),其中P和R分别表示准确率(precision)和召回率(recall);否则,使用Dunn Index计算,表示为DI(C)。数学上,Dunn Index定义为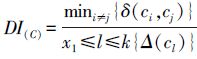
对于NMI和JI指标,值越小意味着不同聚类结果之间的相似度越高;对于F-measure和Dunn Index指标,值越大意味着更高的聚类质量。
6.2 人工数据集使用两种流行的人工数据集评估RLPP的效果,并与其他算法进行比较。第1组人工数据集Syn1分布在二维空间内,分为4部分,每部分由200个数据点组成,共800个数据点。使用数据集Syn1的目的是检验算法是否能够尽可能多的发现可供选择的聚类结果,且所有结果均满足与初始聚类结果正交的条件。第2组人工数据集Syn2的结构较为复杂,每部分的形状都是非凸的。使用数据集Syn2的目的是检验算法是否能够处理非线性的数据结构,并且发掘出嵌入在高维数据中的低维流形结构。
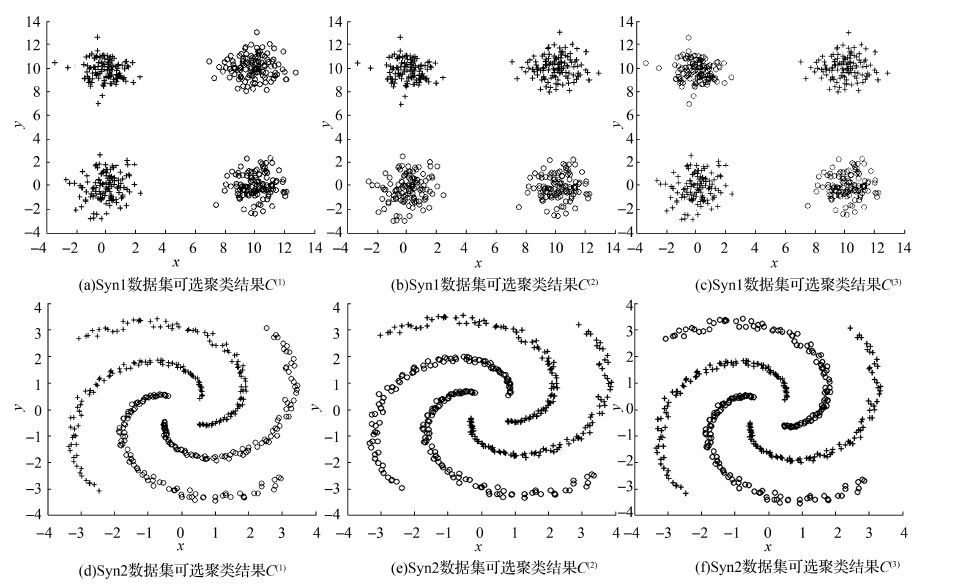
图 1中的第1行表示的是RLPP使用数据集Syn1得到的运行结果。其中,第1列表示的是所提供的参考聚类结果C(1),第2列表示的是由RLPP得到的可供选择的聚类结果C(2)。从图中可以直观地看出,RLPP成功地找到了与所提供的参考聚类结果完全不相同,但是聚类质量很高的可选聚类结果。另外,如果我们把该结果C(2)看作除C(1)外新增的参考聚类结果,并且寻找第2个可选的参考聚类结果C(3),RLPP会得到第3列所显示的聚类结果。C(3)在欧氏距离下与前两个聚类结果相比不是特别得自然,但是C(3)仍然很有启发性,并且它完全独立于前2个参考聚类结果C(1)和C(2)。同时注意到,RPCA算法无法寻找出合适的C(3)。在表 1中,提供了这些算法的表现。
|
| 图 1 由数据集Syn1(第1行)和Syn2(第2行)得到的可选聚类结果 Fig. 1 Alternative clusterings uncovered from Syn1(1st row) and Syn2(2nd row) datasets |
| 算法 | NMI12 | NMI13 | NMI23 | JI12 | JI13 | JI23 | F12 | F13 | F23 |
| RPCA | 0.00 | \ | \ | 0.33 | \ | \ | 1.00 | \ | \ |
| RegGB | 0.00 | 0.00 | 0.00 | 0.33 | 0.33 | 0.33 | 1.00 | 1.00 | 1.00 |
| RLPP | 0.00 | 0.00 | 0.00 | 0.33 | 0.33 | 0.33 | 1.00 | 1.00 | 1.00 |
| 算法 | NMI12 | NMI13 | NMI23 | JI12 | JI13 | JI23 | F12 | F13 | F23 |
| RegGB | 0.00 | 0.00 | 0.00 | 0.33 | 0.33 | 0.33 | 1.00 | 1.00 | 1.00 |
| RLPP | 0.00 | 0.00 | 0.00 | 0.33 | 0.33 | 0.33 | 1.00 | 1.00 | 1.00 |
6.3 舍尔图数据集
选择文献[11]中所介绍的埃舍尔图(escher image)作为另一个用于寻找多个可选聚类结果实验的数据集。对于人眼来说,埃舍尔图有多种分割结果(即聚类结果)。图 2(a)显示的图片为原始图片,可以看到图中有多只爬行动物,并且聚类时明显可以有多种聚类结果。在分割过程中,图中的每个像素点都表示一个反映了RGB信息的数据点。我们使用k-means对图 2(a)进行聚类。图 2(b)为k-means得到的聚类结果,作为其他算法所需要的参考聚类结果。图 2(c)和图 2(d)分别为RLPP得到的可选聚类结果C(2)和C(3),可以看出图 2(c)中的爬行动物为水平姿势,图 2(d)中的爬行动物为垂直姿势。为了对比,提供了由RegGB算法得到的结果(RPCA算法得到的C(2)与RegGB算法近似,C(3)则效果很差,因此不加入对比)。图 2(e)和图 2(f)为RegGB得到的可选聚类结果C(2)和C(3)。从肉眼观察的角度可以发现,图 2(c)与图 2(e)相比轮廓更加清晰,聚类的效果更好。图 2(d)与图 2(f)相比,

|
| 图 2 埃舍尔图数据集上的图像分割结果 Fig. 2 Image segmentation results on Escher image data |
虽然图 2(f)的结果看似更佳,但是图 2(d)保留了原图中更多的信息,每只爬行动物的轮廓都能够得到保留,这是由于RLPP采用了流形子空间学习技术,能够最大程度地保留原始数据的结构。对每种算法重复运行了10次,表 3给出了这些算法的平均表现。
| 算法 | NMI12 | NMI13 | NMI 23 | JI12 | JI13 | JI 23 | DI12 | DI13 | DI 23 |
| RegGB | 0.05 | 0.27 | 0.26 | 0.39 | 0.33 | 0.28 | 3.81 | 0.05 | 2.38 |
| RLPP | 0.03 | 0.06 | 0.01 | 0.19 | 0.39 | 0.34 | 3.81 | 0.02 | 1.60 |
6.4 CMUFace数据集
使用UCI数据库中的CMUFace数据集检验算法。CMUFace数据集包含20个人的图像,每个人又分为不同的面部表情(正常、高兴、悲伤、生气),不同的头部朝向(向左、向右、向前、向上),不同眼部状况(睁开、墨镜)。每个人有32张图片,包含了上述特征的组合。由于图片中的人的身份是已知的,因此身份信息可以作为参考聚类结果直接使用。随机选取了3个人的全部图像进行试验。
图 3显示的是聚类结果的平均值的图像。其中第1行是原始图像经由k-means算法得到的平均值图像,第2行由RLPP算法得到,第3行和第4行由RPCA与RegGB算法得到。

|
| 图 3 CMUFace数据集上的运行结果 Fig. 3 Results on CMUFace data |
从图像上看,第1行聚类的依据是不同的人,其余3行聚类的依据是人不同的头部朝向。很明显,3种算法都从数据集中得到了另一组完全不同,但是同等重要的聚类结果。从图中可以看出,RLPP和RPCA的聚类效果最好,RegGB稍差。表 4是这3种算法的对比。
| 算法 | NMI | JI | F |
| RPCA | 0.012 4 | 0.294 1 | 0.713 9 |
| RegGB | 0.669 0 | 0.444 4 | 0.751 2 |
| RLPP | 0.076 6 | 0.215 1 | 0.702 1 |
6.5 算法运行时间
实验均在MARTLAB 8.1.0.604 (R2013a)平台下完成,操作系统为64位Windows7,CPU为Intel(R) Core(TM) i3-3240 3.40G Hz,内存为4 GB。
对于人工数据集Syn1和Syn2,RLPP算法发掘出一个可供选择的聚类结果分别耗时3.4 s和2.9 s。对于Esher图,由于聚类之前需要进行图像一维化处理,因此数据集的维数很大,共耗时136 s。对于CMUFace数据集,RLPP算法找到一个可供选择的聚类结果共耗时2.7 s。以上运行时间均为运行10次试验的平均时间。
上述运行时间表明本文算法在合适的数据集上是完全适用的,但是在数据集规模很大的情况下,仍存有改进的空间。
7 结束语本文提出了一种新的算法RLPP,采用子空间流形学习技术,寻找可供选择的聚类结果。RLPP算法的优势在于最终能够转化为特征分解问题,也就是说可以找到封闭解,并且子空间一定是全局最优的,这也是本文区别于其他相关研究的重要特点之一。在文章中对RLPP算法进行了论证和实验,并对比了目前效果最好的著名算法。实验结果表明RLPP算法的性能不输于甚至优于其他算法。对于如何更好地选取最小特征值的个数k,以及如何降低算法在处理维数较大数据时的时间复杂度,都是继续研究的方向。
| [1] | DANG Xuanhong, BAILEY J. Generating multiple alternative clusterings via globally optimal subspaces[J]. Data mining and knowledge discovery , 2014, 28 (3) : 569-592 DOI:10.1007/s10618-013-0314-1 |
| [2] | GRETTON A, BOUSQUET O, SMOLA A, et al. Measuring statistical dependence with Hilbert-Schmidt norms[M]//JAIN S, SIMON H U, TOMITA E. Algorithmic Learning Theory. Berlin Heidelberg:Springer, 2005:63-77. |
| [3] | HE Xiaofei, NIYOGI X. Locality preserving projections[C]//Advances in Neural Information Processing Systems. Vancouver, Canada, 2003, 16:153-160. |
| [4] | BAE E, BAILEY J. COALA:a novel approach for the extraction of an alternate clustering of high quality and high dissimilarity[C]//Proceedings of the 6th International Conference on Data Mining. Hong Kong, China, 2006:53-62. |
| [5] | GONDEK D, HOFMANN T. Non-redundant data clustering[J]. Knowledge and information systems , 2007, 12 (1) : 1-24 DOI:10.1007/s10115-006-0009-7 |
| [6] | JAIN P, MEKA R, DHILLON I S. Simultaneous unsupervised learning of disparate clusterings[J]. Statistical analysis and data mining:the ASA data science journal , 2008, 1 (3) : 195-210 DOI:10.1002/sam.v1:3 |
| [7] | DANG Xuanhong, BAILEY J. Generation of alternative clusterings using the CAMI approach[C]//Proceedings of the SIAM International Conference on Data Mining, SDM 2010. Columbus, Ohio, USA, 2010, 10:118-129. |
| [8] | DANG Xuanhong, BAILEY J. A hierarchical information theoretic technique for the discovery of non linear alternative clusterings[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, DC, USA, 2010:573-582. |
| [9] | VINH N X, EPPS J. MinCEntropy:a novel information theoretic approach for the generation of alternative clusterings[C]//Proceedings of the IEEE International Conference on Data Mining. Sydney, Australia, 2010:521-530. |
| [10] | COVER T M, THOMAS J A. Elements of information theory[M]. Chichester: John Wiley & Sons, 2012 . |
| [11] | KAPUR J N. Measures of information and their applications[M]. New York: Wiley-Interscience, 1994 . |
| [12] | PRINCIPE J C, XU D, FISHER J. Information theoretic learning[M]//HAYKIN S. Unsupervised Adaptive Filtering. New York:Wiley, 2000, 1:265-319. |
| [13] | PARZEN E. On estimation of a probability density function and mode[J]. The annals of mathematical statistics , 1962, 33 (3) : 1065-1076 DOI:10.1214/aoms/1177704472 |
| [14] | CUI Ying, FERN X Z, DY J G. Non-redundant multi-view clustering via orthogonalization[C]//Proceedings of the 7th IEEE International Conference on Data Mining. Omaha, Nebraska, USA, 2007:133-142. |
| [15] | DAVIDSON I, QI Zijie. Finding alternative clusterings using constraints[C]//Proceedings of the 8th IEEE International Conference on Data Mining. Pisa, Italy, 2008:773-778. |
| [16] | QI Zijie, DAVIDSON I. A principled and flexible framework for finding alternative clusterings[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France, 2009:717-726. |
| [17] | DASGUPTA S, NG V. Mining clustering dimensions[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel, 2010:263-270. |
| [18] | NIU Donglin, DY J G, JORDAN M I. Multiple non-redundant spectral clustering views[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel, 2010:831-838. |



