近年来,随着机器人技术、网络通信技术和自动控制技术的不断发展,多移动机器人系统协调控制研究引起了众多领域研究者的关注, 并在军事、空间探索、交通控制、医疗与服务行业等领域展现了广阔的应用前景[1]。作为多机器人系统协调控制的最基础和最重要的研究问题之一,编队控制是指空间分布的多个机器人,达到控制目标的同时,保持期望的空间队形,同时要适应环境约束 (例如存在障碍物或者空间的物理限制) [2]。
编队控制所考察的机器人主要包括:地面移动机器人[3-4]、无人飞行器[5-7]、卫星[8]和自主式潜水器[9-10]等。对于期望队形的实现问题,控制算法主要有:基于行为法[3-4]、虚拟结构法[11-13]和领航跟随法[14-16]。此外,对于多移动机器人系统来说,避障问题也是编队中需要考虑的一个重要问题。在有障碍物的约束环境下,多移动机器人的编队避障控制会变得更加复杂,因为移动机器人既要保持整体队形,又要合理躲避障碍物。对于未知环境下的机器人避障问题,已经有很多有效的解决方法。文献[17]提出人工势场法,基本原理是构造机器人和障碍物、目标点间的力场,机器人将在目标点的引力和障碍物的斥力的合力作用下运动。势场法存在若干缺陷,机器人在相近障碍物间不能找到路径,易在障碍物前震荡,在狭窄通道中摆动[18]。为解决这些问题,文献[19]提出了向量场直方图法 (vector field histogram:VFH),该方法将障碍物对机器人的影响量化为机器人各个角度上的障碍强度值,在障碍强度值低于阈值的角度范围内选择移动方向。VFH法存在阈值敏感问题,阈值过小时,一些可行通道被忽略,阈值过大时,不一定发现前方障碍物[20]。
本文采用领航-跟随编队控制算法来解决多移动机器人系统的编队控制问题。为使得多移动机器人系统能够成功地进行编队和避障,还采用了一种极坐标系下基于障碍物密度的Ploar Histogram避障算法,该避障策略可有效避免VFH法中存在阈值敏感问题。最后,通过3个Qbot移动机器人的实验验证了所提算法的有效性。
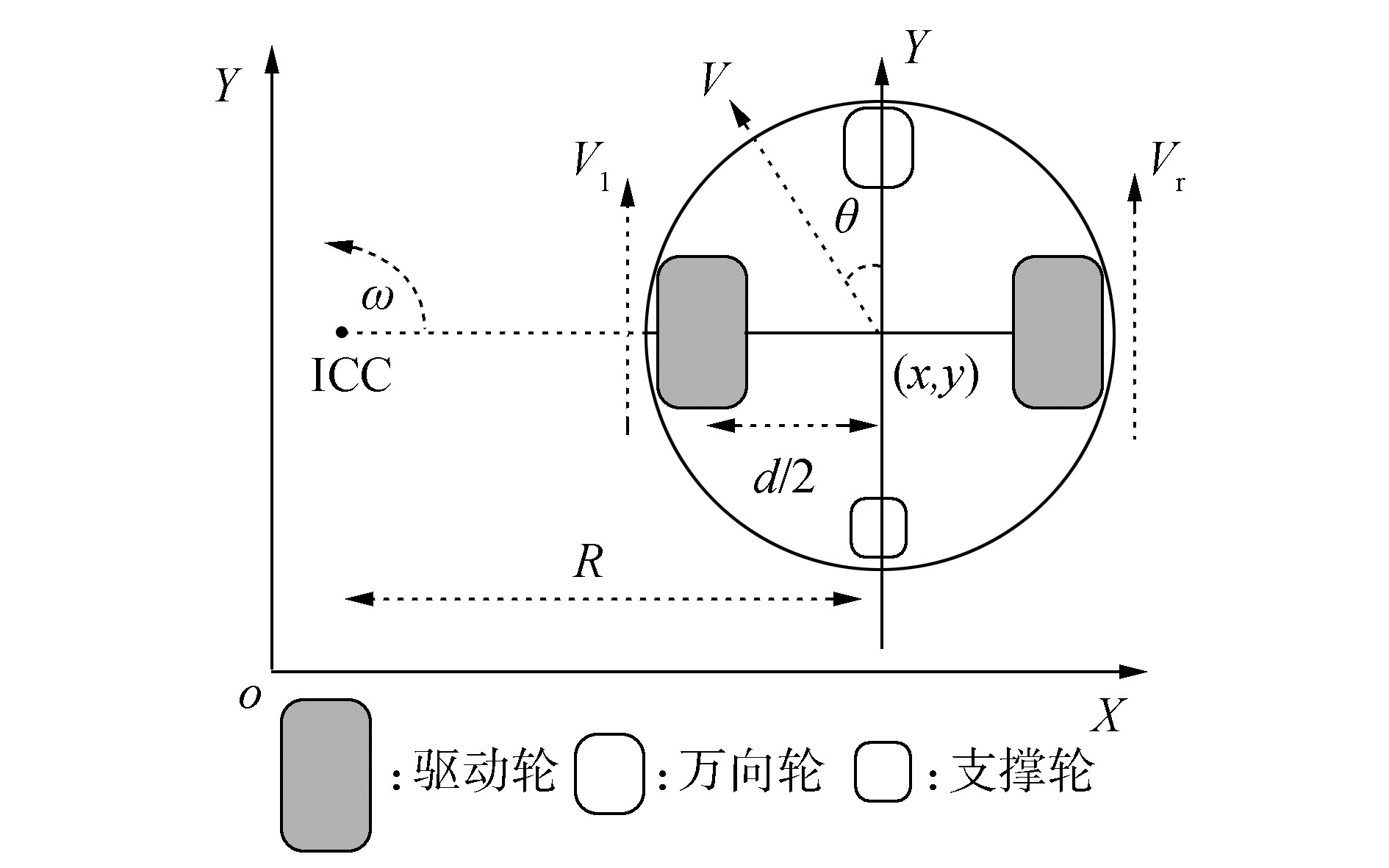
1 两轮差分驱动机器人运动学本文考察的是Quanser公司提供的Qbot移动机器人,属于差分驱动轮式移动机器人,假设其质心与两驱动轮轴中心重合。在轮式移动机器人的理论研究中,一般都是假设车轮与地面之间点接触,且接触点和地面之间只有纯滚动没有相对的滑动 (包括纵向与侧向滑动),这种理想条件使得机器人受到非完整约束。可根据刚体力学法求得两轮差动移动机器人的运动学模型。
差分驱动机器人向前或向后运动时,左右驱动轮的速度相等;当左右驱动轮之间存在速度差时,机器人将会绕左 (或右) 驱动轮轴线上某一点旋转,该点称为瞬时曲率中心ICC (Instantaneous Center of Curvature),如图 1所示。机器人的运动轨迹可以通过改变两驱动轮的速度进行控制。
|
| 图 1 两轮差分机器人运动学 Fig. 1 Two differential robot kinematics |
机器人状态可由左右驱动轮轴中点坐标 (x, y) 和航向角θ表示。
由图 1可得:
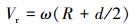 |
(1) |
 |
(2) |
 |
(3) |
式中:Vl和Vr分别为左右驱动轮的速度,V为机器人线速度 (假设机器人速度V大于等于零),ω为机器人绕ICC的旋转角速度,R为左右驱动轮轴心到曲率中心的距离,d为左右驱动轮中心之间的距离。由式 (1),(2) 变形可得:
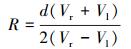 |
(4) |
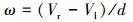 |
(5) |
机器人的正向运动学描述了机器人速度与位置状态之间的关系,在给定左右驱动轮速度和机器人初始位姿 (x, y, θ)t=0的情况下,可以求得任意时刻t时的机器人的位姿 (x, y, θ)t=t。
下面介绍机器人相对初始状态的位姿[21]。
已知机器人速度V(t) 和航向角θ(t),机器人在t=0时刻的初始位姿为 (0, 0, 0),受非完整约束条件下的轮式机器人存在如下关系:
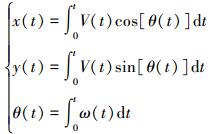 |
(6) |
由式 (6) 可得机器人在t+δt的位姿:
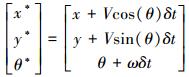 |
(7) |
式中:(x, y, θ) 和 (x*, y*, θ*) 分别为t时刻和t+δt时刻机器人的位姿。由式 (7) 可知,通过改变线速度V和角速度ω可以控制移动机器人的运动轨迹。
对于两轮差动机器人将式 (3) 和 (5) 带入方程 (6) 可得:
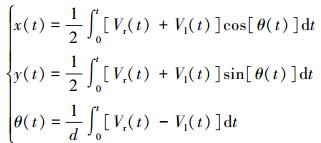 |
(8) |
同样由式 (8) 化简可得:
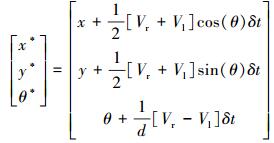 |
(9) |
由式 (8) 和式 (9) 可知,对于两轮差动机器人通过改变左右驱动轮的速度Vl和Vr就能控制移动机器人的运动轨迹。本文通过控制Vr和Vl来驱动机器人,实现编队控制。
2 领航-跟随编队控制结构领航-跟随编队控制法是指定编队中的某一机器人作为领航者,其他机器人作为跟随者跟随领航机器人运动。在多移动机器人系统中,一般设定一个主领航机器人,负责提供编队的导航,决定编队的主轨迹。如果系统中的两个机器人存在局部的领航与跟随关系,则分别称这两个机器人为领航机器人和跟随机器人。
领航-跟随法主要有l-l和l-φ两种编队模式[22]。l-l法至少需要3个机器人,即跟随机器人以固定的距离l跟随两个领航机器人,保持期望的队形,实现多移动机器人的编队控制。l-φ控制方法的思想是跟随机器人要以一定的距离和角度跟随领航机器人,实现期望队形的编队控制。如图 2所示,控制目标是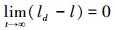


|
| 图 2 领航-跟随队形结构模型 Fig. 2 Leader-follower formation structure model |
本文在l-φ控制法的基础上引入虚拟跟随机器人,跟随机器人与领航机器人保持期望的队形结构,只要跟随机器人运动到虚拟跟随机器人的位置,就可以实现期望的队形编队控制[23]。如图 3所示,(xl, yl, θl) 为领航机器人位姿,(xf, yf, θf) 为跟随机器人位姿,跟随距离和角度分别为l和φ,可得虚拟跟随机器人位姿 (xv, yv, θv) 为

|
| 图 3 领航-虚拟跟随队形结构模型 Fig. 3 Leader-virtual follower formation structure model |
 |
(10) |
将 (xv, yv, θv) 作为跟随机器人的目标点带入式 (9) 可得:
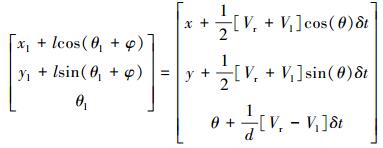 |
(11) |
式中 (x, y, θ) 为跟随机器人当前位姿,由式 (11) 得:
 |
(12) |
式中:xv=xl+lcos (θl+φ), yv=yl+lsin (θl+φ), θv=θl。令

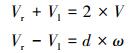 |
(13) |
由式 (13) 可得:
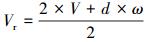 |
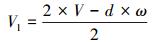 |
(14) |
式 (14) 即为编队中的跟随机器人的左右驱动轮输入。
虚拟跟随机器人的引入,将队形保持转换为跟随机器人对于虚拟跟随机器人的跟踪控制,这种队形保持模型,可描述任意队形结构。
3 避障算法VFH避障算法通过构建向量场直方图来确定可行方向 (如图 4)[19]。VFH算法采用栅格模型,机器人的工作空间划分为若干连续的二维栅格,将机器人感知的360°范围划分为n个扇区,每个扇区的夹角为360°/n,通过VFH法中定义的极线障碍强度值计算方法,计算对应扇区的极线障碍强度值Hk(k=0, 1, …, n-1)。图 4为计算后得到的直方图示例,直方图上的每一个Hk可视为k扇区内障碍物的密度,Hk越大说明扇区内障碍物越密集。在直方图上,设定阈值δ,若扇区k的Hk值低于δ则视为无障碍区,若干个无障碍扇区构成候选区 (Valley),图 4(以0°~180°为例) 中根据直方图和阈值δ将得到4个候选区,机器人根据候选区的宽度判断其是否可以通过,在所有可以通过的候选区中,选择最接近目标的一个通过。该方法的不足之处是对阈值敏感,阈值δ过大时可能会碰到障碍物,过小则可能一些可行通道将被忽略。
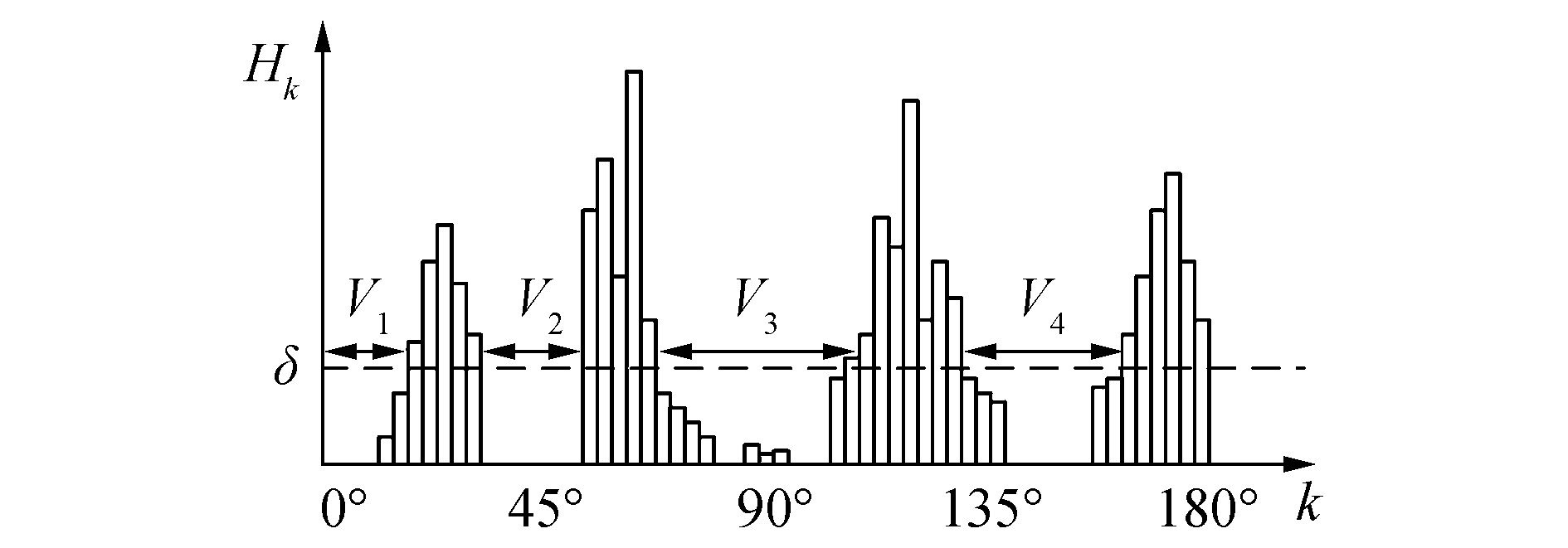
|
| 图 4 向量场直方图 Fig. 4 Vector field histogram |
针对以上不足之处,本文利用红外线测距传感器获取局部环境信息,采用一种基于极坐标系下障碍物密度的避障方法Ploar Histogram避障法。该算法根据障碍密度搜索一条最安全的导航方向,利用红外测距传感器所测数据 (即距障碍物距离) 来设计障碍密度值,选择障碍密度最小的方向作为机器人的安全导航方向。如图 5所示,其中图 5(a)表示位于0°、45°、90°、135°和180°方向的5个传感器获得的障碍物距离数据 (m),其中90°方向为机器人的正前方。
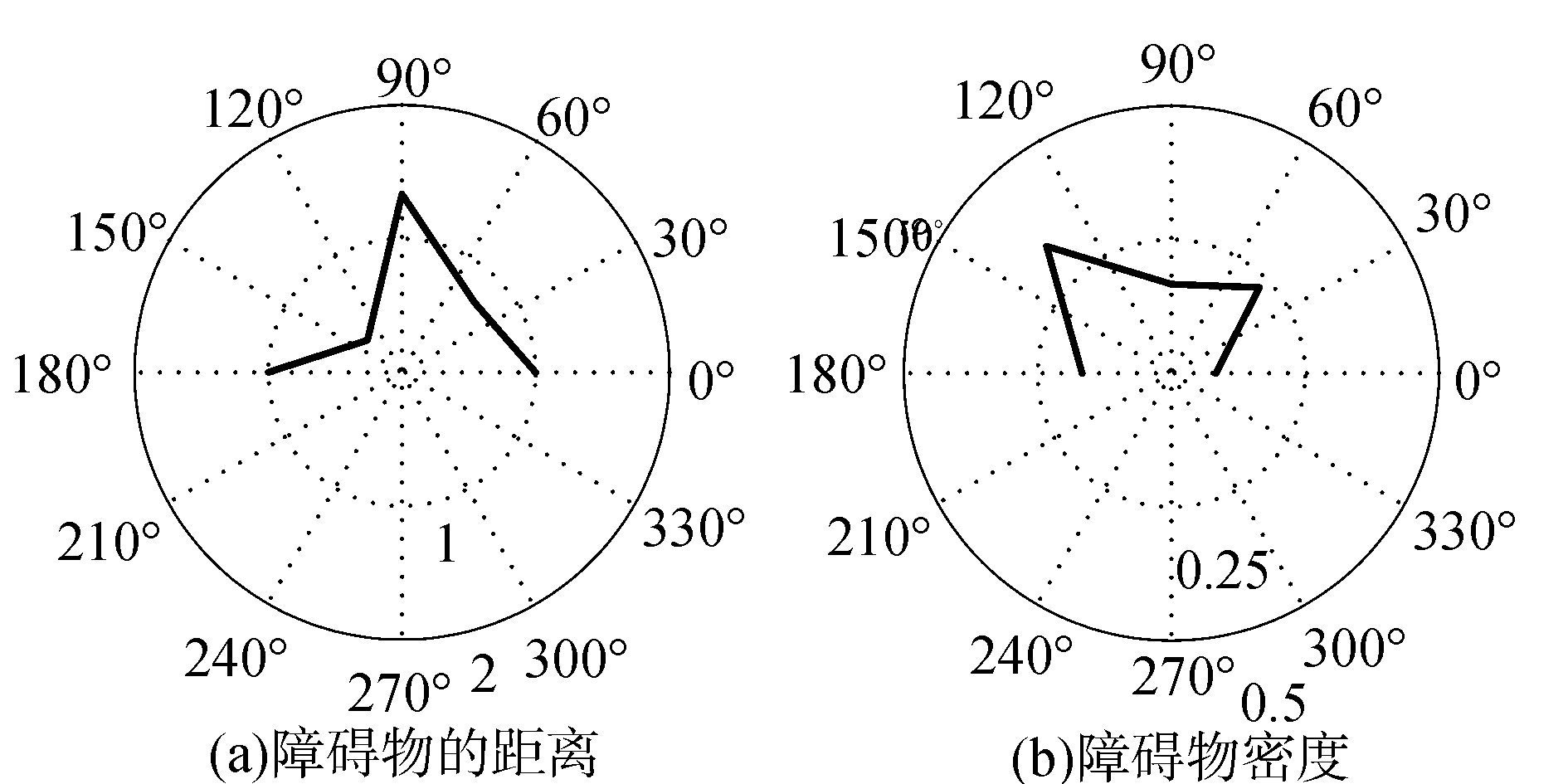
|
| 图 5 极坐标下的障碍物距离及障碍物密度 Fig. 5 Polar plots of range data and obstacle density |
图 5(b)表示相应方向上的极坐标障碍物密度值 (POD),其计算方法如下:
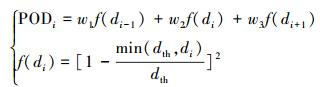 |
(15) |
 |
(16) |
式中:i=1, 2, …, 5表示第i个传感器,指向45×(i-1)°方向,di表示第i个传感器获得的障碍物距离,dth为传感器所能检测的最大距离,f (di) 为第i个传感器获得的障碍密度值,w1、w2和w3为权重因子 (w1+w2+w3=1.0),且有w2>w1, w2>w3,表征某方向上的障碍密度值受该方向上的传感器所获得的障碍密度值的影响大于其两侧传感器所获得的障碍密度值。
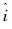
为验证算法的实际有效性,本文以基于iRobot的Create平台开发的自主移动机器人Qbot为研究对象,其带有5个红外传感器,分别安装在机器人的0°、45°、90°、135°和180°方向上,如图 6所示,搭建Quanser无人工具实验系统仿真平台,进行半实物仿真实验。

|
| 图 6 Qbot实物图 Fig. 6 Qbot physical figure |
实验系统大致包括以下几部分,如图 7所示:
|
| 图 7 Quanser无人工具实验系统 Fig. 7 Quanser unmanned tool experiment system |
1) QuaRc实时控制软件与多智能体任务开发系统;
2) 地面控制站;
3) 无人地面机器人;
4) 照相机定位系统。
QuaRC实时控制软件与Matlab/Simulink兼容,可以方便地调用Matlab/Simulink中的函数。将设计的控制器与相应的系统硬件端口Simulink模块相连,编译并下传到QuaRC中,实现实时控制。地面控制站是通过一台地面控制计算机来实现,包括定位、多智能体控制等,主控制机通过无线局域网和各个智能体进行通信,地面控制站主要进行任务规划和定位等目的,一旦控制系统的控制算法设计完成,控制站就只起到定位作用。无人地面机器人是基于iRobot的Create平台开发的自主移动机器人Qbot,它带有5个红外线传感器,可以用于探测障碍物,探测距离最大可达。照相机定位系统通过8个红外照相机实现空间的三维定位。
4.2 实验原理系统采用Host-Target工作模式进行实时控制,控制器开发在装有MATLAB/Simulink的主机上实现,控制器搭建完成后,在Simulink下进行编译并且下载到移动机器人的控制器 (target) 中实现实时控制。主机Host可同时控制多个控制器 (Target),从而可以在MATLAB环境下进行多智能体控制算法的研究。每个移动机器人上都装有3个红外线反射球,使装在墙壁上的8台红外照相机可以实时捕捉每个移动机器人的位姿坐标 (x, y, θ),通过主机Host和无线网络传输给每个移动机器人,跟随机器人按预先设计好的算法计算出与领航机器人的位置差,调整方向跟踪领航机器人以实现编队控制。编队过程中,领航和跟随机器人通过自身携带的红外线传感器检测环境中的障碍物,机器人根据检测到的障碍物情况利用Polar Histogram避障控制策略实时避开障碍物,实现编队避障控制。
4.3 算法实现步骤1) 在主机Host上设计领航机器人的跟踪路径。建立无线局域网。
2) 主机Host实时地将照相机定位系统捕捉到的领航和跟随机器人的位姿信息发送给对应的领航和跟随机器人,同时将设计好的路径命令发送给领航机器人。
3) 领航机器人实时接收主机传来的路径命令和自身位姿信息向目标点运行,当自身携带的红外线传感器检测到障碍物时,利用设计好的避障算法进行避障,绕过障碍后继续驶向目标点。同时,领航机器人根据l-φ控制法生成虚拟机器人的轨迹命令,并发送给跟随机器人。
4) 跟随机器人实时接收主机Host发送的自身位姿信息和领航机器人发送的虚拟机器人轨迹命令,跟随机器人沿着虚拟跟随机器人的轨迹跟随领航机器人,同时能够有效避开环境中的障碍物,实现编队避障控制。
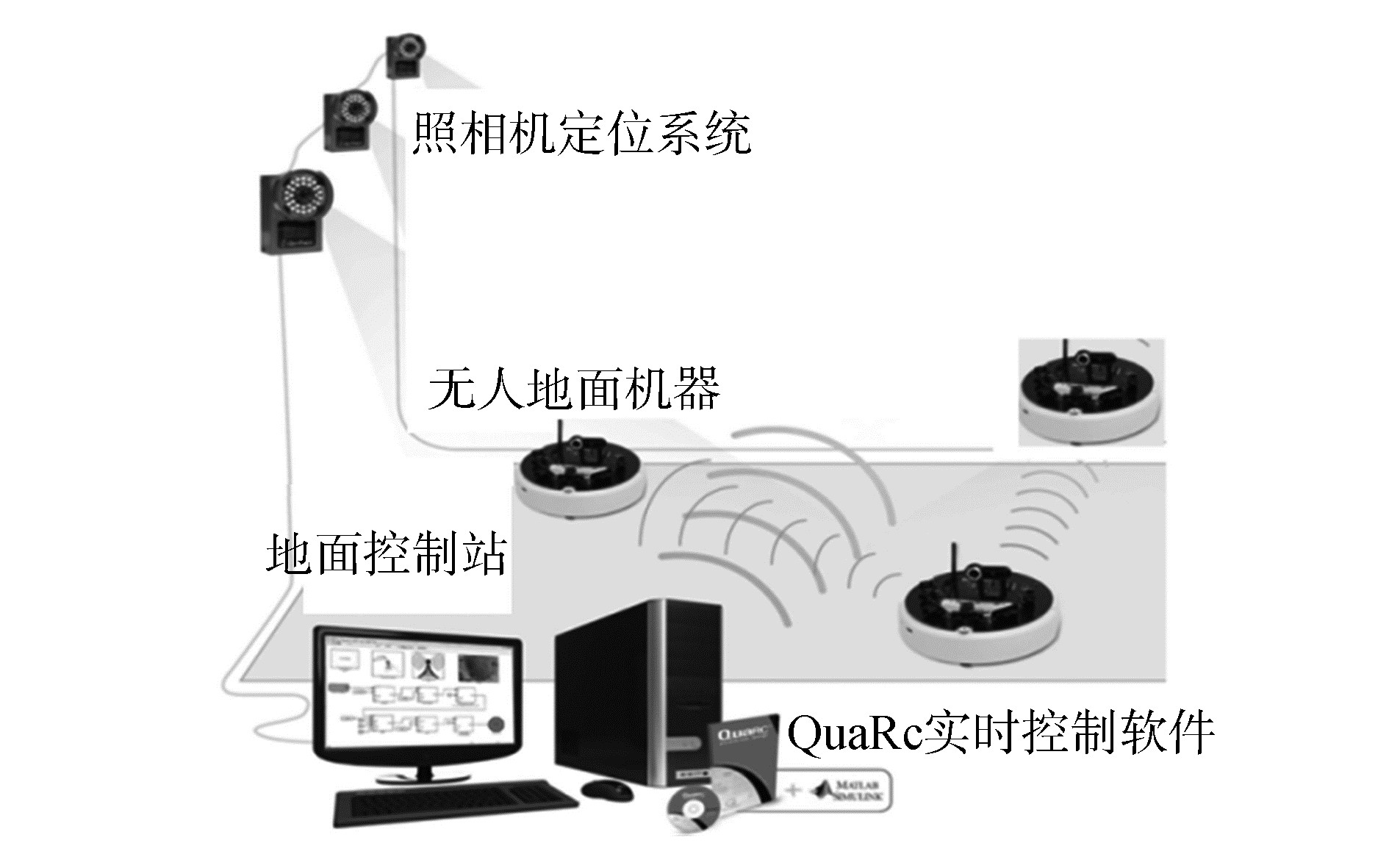
4.4 半实物仿真实验及结果分析设计一个3 m×3 m的场地,构造机器人编队避开障碍物到达目标点的仿真环境,利用领航跟随编队法和Polar Histogram避障法,分别进行了3个机器人柱形编队避障控制实验和3个机器人三角形编队避障控制实验,柱形和三角形编队队形如图 8所示。
|
| 图 8 多移动机器人的编队队形 Fig. 8 Formation of multiple mobile robots |
实验中设置机器人的红外传感器探测距离dth=0.4 m,控制周期为0.1 s,Qbot两驱动轮之间的距离d=252.5 mm。
实验1 3个Qbot移动机器人柱形编队避障实验
在主机Host上设计领航机器人从任意初始位置,经中间点 (0.9,0.9)、(-0.9,0.9)、(-0.9,-0.9) 和 (0.9,-0.9) 运动到目标点 (0.9,0.9)。障碍物为长方体和圆柱体障碍物,位置任意摆放在路径当中。编队队形为柱形,跟随机器人RF1和RF2与领航机器人RL的期望相对距离分别为0.4 m和0.8 m,相对方位角都为φ=180°。图 9是3个Qbot柱形编队实验过程的部分截图,可以看出两跟随机器人可以跟随领航机器人从初始位置,经中间点 (0.9,0.9)、(-0.9,0.9)、(-0.9,-0.9) 和 (0.9,-0.9) 运动到目标点 (0.9,0.9),并且可以顺利避开障碍物。

|
| 图 9 柱形编队避障过程 Fig. 9 Cylindrical formation process of obstacle avoidance |
编队轨迹如图 10(a)所示,两跟随机器人RF1和RF2跟随领航机器人RL保持柱形编队顺利避开障碍物达到目标点,领航机器人运动的轨迹即为跟随机器人期望的跟踪轨迹。领航机器人RL和跟随机器人RF1、RF2的左右轮速度控制输入如图 10(b)、(d)和 (f) 所示,可以看出各机器人的左右轮速度控制输入是时变的,当机器人转弯或遇障碍物变向时,各机器人左右轮速度变化较大。领航机器人RL的位姿如图 8(c)所示,领航机器人跟踪点 (0.9,0.9)、(-0.9,0.9)、(-0.9,-0.9) 以及 (0.9,-0.9) 最终到达目标点 (0.9,0.9),其中在遇到障碍物时机器人偏离期望轨迹存在误差,但随着编队的进行,机器人回归期望轨迹,误差趋近于0。跟随机器人RF1和RF2的位姿如图 10(e)和(g)所示,跟随机器人都以较小的误差跟随虚拟机器人 (即领航机器人的轨迹),完成轨迹跟踪控制并且可以实时避开障碍物。

|
| 图 10 3个机器人柱形编队控制实验 Fig. 10 Three robots cylindrical formation control experiment |
实验2 3个Qbot移动机器人三角形编队避障实验。
设计领航机器人RL从初始位置点 (0,0),经中间点 (0,0.6) 和 (0,1.6) 最终到达目标点 (0,2.2)。引入虚拟跟随机器人Rv1和Rv2分别与领航机器人RL保持相对距离为0.5 m与0.5 m,相对期望角为135°与-135°。跟随机器人RF1和RF2分别跟随虚拟跟随机器人Rv1与Rv2。
图 11是3个Qbot三角形编队避障实验过程的部分截图,可以看出机器人小组在保持三角形编队的同时也可以顺利避开障碍物。

|
| 图 11 三角形编队避障过程 Fig. 11 Triangle formation process of obstacle avoidance |
编队轨迹如图 12(a)所示,机器人队形为三角形,前进一段时间后,编队遇到障碍物,领航和跟随机器人各自避开障碍物后,继续以三角形编队到达目标点。领航机器人RL和跟随机器人RF1、RF2的左右轮速度控制输入如图 12(b)、(d)和 (f) 所示,可以看出,各机器人的左右轮速度控制输入是时变的,当机器人转弯或遇障碍物变向时,各机器人左右轮速度变化较大。领航机器人的位姿如图 12(c)所示,领航机器人在初始位置 (0,0) 跟踪中间点 (0,0.6) 和 (0,1.6) 最终到达目标点 (0,2.2),在避障时,机器人偏离期望跟踪点存在误差,但随着编队的进行,机器人回归期望跟踪轨迹,误差趋近于0。跟随机器人RF1和RF2的位姿如图 12(e)和(g)所示,跟随机器人RF1和RF2都以较小的误差跟踪虚拟跟随机器人Rv2与Rv1的轨迹,同时可以顺利避开障碍物,完成编队控制。

|
| 图 12 3个机器人三角形编队控制实验 Fig. 12 Three robots triangle formation control experiment |
实验3 3个Qbot移动机器人队形变换避障实验
图 13为3个Qbot队形变换的编队避障实验过程的部分截图。

|
| 图 13 队形变换编队避障过程 Fig. 13 Formation transformation process of obstacle avoidance |
设计领航机器人RL从初始位置点为 (0,0),经中间点 (0,0.4) 和 (0,1.7) 最终到达目标点 (0,2.2)。无障碍环境下,虚拟跟随机器人Rv1和Rv2分别与领航机器人RL保持相对距离为0.5 m与0.5 m,对应的相对期望角为135°与-135°。存在障碍的环境下,虚拟跟随机器人Rv1和Rv2分别与领航机器人RL保持相对距离为0.3 m与0.6 m,对应的相对期望角均为0°。跟随机器人RF1和RF2分别跟随虚拟跟随机器人Rv1与Rv2。在未发现障碍物时,机器人小组保持三角形编队队形行驶;当检测到障碍物时,机器人小组变换为柱形编队,在跟随机器人紧跟领航机器人穿过障碍物后,机器人小组恢复三角形编队到达目标点。
3个机器人队形变换编队控制实验如图 14所示。
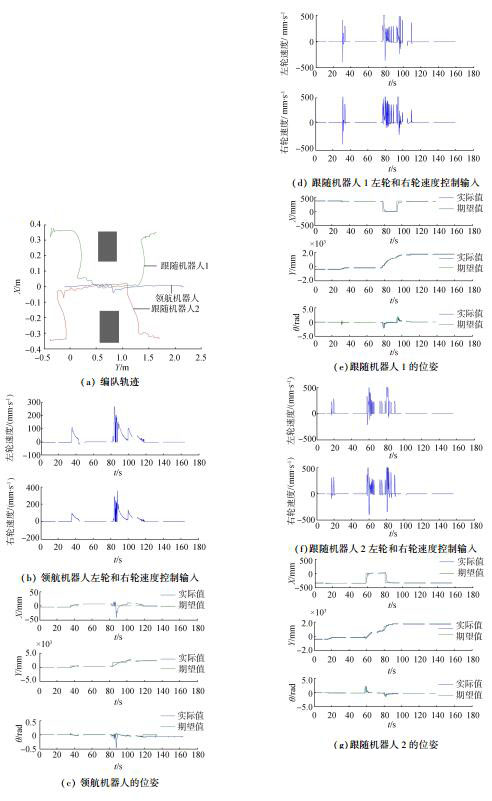
|
| 图 14 3个机器人队形变换编队控制实验 Fig. 14 Three robots formation transformation control experiment |
编队轨迹如图 14(a)所示:机器人初始以三角形队形前进;在检测到障碍物后,队形变换为柱形通过障碍区;安全避障后,恢复三角形编队到达目标点。
领航机器人RL和跟随机器人RF1,RF2的左右轮速度控制输入如图 14(b),(d) 和 (f) 所示:各机器人的左右轮速度控制输入是时变的,当机器人转弯或遇障碍物变向时,各机器人左右轮速度变化较大。领航机器人的位姿如图 14(c)所示:领航机器人在初始位置 (0,0) 跟踪中间点 (0,0.4) 和 (0,1.7) 最终到达目标点 (0,2.2);避障时,机器人偏离期望跟踪点存在偏差,但随着编队的进行,机器人回归期望跟踪轨迹,误差趋近于0。跟随机器人RF1和RF2的位姿如图 14(e)和(g)所示:跟随机器人RF1和RF2都以较小的误差跟踪虚拟跟随机器人Rv2与Rv1的轨迹,完成编队控制。
从上述实验过程能够看出,机器人小组可以保持某单一队形完成编队避障控制,也可以根据环境的约束自主变换队形。机器人小组在选择更安全的队形通过障碍区后,自主恢复到初始队形,最终顺利到达目标点,完成编队避障控制。
6 结束语本文以两轮差动机器人为研究对象,提出了在障碍环境中的多移动机器人的编队控制方法,通过引入虚拟跟随机器人,将编队控制转化为跟踪控制,此外,通过编队中的领航和跟随机器人携带的红外线传感器自主感知获取外部环境信息,采用Polar Histogram避障法,引导多机器人编队智能地避开障碍物,实现了多移动机器人的编队避障控制,该避障策略不存在阈值敏感性问题,因而对复杂的环境也具有很好的适应性。利用Quanser无人工具实验系统仿真平台,分别对柱形编队、三角形编队以及队形变换编队进行实物实验,由仿真实验结果可看出本文所提出的控制方法的有效性,多移动机器人既可以保持编队队形,同时各机器人也可以自主避障,实现多移动机器人协调编队和避障控制。
| [1] | FARINELLI A, LOCCHI L, NARDI D. Multirobot systems: a classification focused on coordination[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2004, 34(5): 2015-2028. DOI:10.1109/TSMCB.2004.832155. |
| [2] |
王祥科, 李迅, 郑志强. 多智能体系统编队控制相关问题研究综述[J].
控制与决策, 2013, 28(11): 1601-1613.
WANG Xiangke, LI Xun, ZHENG Zhiqiang. Survey of developments on multi-agent formation control related problems[J]. Control and decision, 2013, 28(11): 1601-1613. |
| [3] |
杨帆, 刘士荣, 董德国. 编队控制中的机器人行为与基于服务的运动行为结构设计[J].
机器人, 2012, 34(1): 120-128.
YANG Fan, LIU Shirong, DONG Deguo. Robot behavior and service-based motion behavior structure design in formation control[J]. Robot, 2012, 34(1): 120-128. |
| [4] | ARRICHIELLO F, CHIAVERINI S, INDIVERI G, et al. The null-space-based behavioral control for mobile robots with velocity actuator saturations[J]. The international journal of robotics research, 2010, 29(10): 1317-1337. DOI:10.1177/0278364909358788. |
| [5] |
宋敏, 魏瑞轩, 沈东, 等. 基于非线性动态逆的无人机编队协同控制[J].
控制与决策, 2011, 26(3): 448-452.
SONG Min, WEI Ruixuan, SHEN Dong, et al. UAV formation control based on nonlinear dynamic inversion[J]. Control and decision, 2011, 26(3): 448-452. |
| [6] |
李少斌, 陈炎财, 杨忠, 等. 具有通信延迟的多无人机编队飞行控制[J].
信息与控制, 2012, 41(2): 142-146.
LI Shaobin, CHEN Yancai, YANG Zhong, et al. Formation fight control of multi-UAVs with communication delay[J]. Information and control, 2012, 41(2): 142-146. |
| [7] |
魏瑞轩, 茹常剑, 祁晓明. 通信延迟条件下无人机编队重构的自主安全控制[J].
控制理论与应用, 2013, 30(9): 1099-1108.
WEI Ruixuan, RU Changjian, QI Xioaming. Autonomous safety control of unmanned aerial vehicle formation reconfiguration under communication delay[J]. Control theory & applications, 2013, 30(9): 1099-1108. |
| [8] |
吴锦杰, 刘昆, 韩大鹏, 等. 基于对偶四元数的卫星主从式编队姿轨跟踪的优化控制[J].
控制理论与应用, 2013, 30(9): 1069-1078.
WU Jinjie, LIU Kun, HAN Dapeng, et al. Optimized tracking-control for attitude and orbit of satellite formation flying using dual quaternion[J]. Control theory & applications, 2013, 30(9): 1069-1078. |
| [9] | WANG Y, YAN W, LI J. Passivity-based formation control of autonomous underwater vehicles[J]. IET control theory & applications, 2012, 6(4): 518-525. |
| [10] |
王银涛, 严卫生. 多自主水下航行器系统一致性编队跟踪控制[J].
控制理论与应用, 2013, 30(3): 379-384.
WANG Yintao, YAN Weisheng. Consensus formation tracking control of multiple autonomous underwater vehicle systems[J]. Control theory & applications, 2013, 30(3): 379-384. |
| [11] | REN Wei, SORENSEN N. Distributed coordination architecture for multi-robot formation control[J]. Robotics and autonomous systems, 2008, 56(4): 324-333. DOI:10.1016/j.robot.2007.08.005. |
| [12] | GHOMMAM J, MEHRJERDI H, SAAD M, et al. Formation path following control of unicycle-type mobile robots[J]. Robotics and autonomous systems, 2010, 58(5): 727-736. DOI:10.1016/j.robot.2009.10.007. |
| [13] | MEHRJERDI H, GHOMMAM J, SAAD M. Nonlinear coordination control for a group of mobile robots using a virtual structure[J]. Mechatronics, 2011, 21(7): 1147-1155. DOI:10.1016/j.mechatronics.2011.06.006. |
| [14] | CONSOLINI L, MORBIDI F, PRATTICHIZZO D, et al. Leader-follower formation control of nonholonomic mobile robots with input constraints[J]. Automatica, 2008, 44(5): 1343-1349. DOI:10.1016/j.automatica.2007.09.019. |
| [15] | SHAO J, XIE G, WANG L. Leader-following formation control of multiple mobile vehicles[J]. IET control theory & applications, 2007, 1(2): 545-552. . |
| [16] |
杨丽, 曹志强, 谭民. 不确定环境下多机器人的动态编队控制[J].
机器人, 2010, 32(2): 283-288.
YANG Li, CAO Zhiqiang, TAN Min. Dynamic formation control for multiple robots in uncertain environments[J]. Robot, 2010, 32(2): 283-288. |
| [17] | KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[C]//Proceedings of 1985 IEEE International Conference on Robotics and Automation. St. Louis, MO, USA: IEEE, 1985: 500-505. |
| [18] |
章苏书, 吴敏, 曹卫华. 一种局部动态环境下的避障算法[J].
计算技术与自动化, 2003, 22(1): 12-16.
ZHANG Sushu, WU Min, CAO Weihua. An obstacle avoidance algorithm in local dynamic environments[J]. Computing technology and automation, 2003, 22(1): 12-16. |
| [19] | BORENSTEIN J, KOREN Y. The vector field histogram-fast obstacle avoidance for mobile robots[J]. IEEE transactions on robotics and automation, 1991, 7(3): 278-288. DOI:10.1109/70.88137. |
| [20] |
李云翀, 何克忠. 基于激光雷达的室外移动机器人避障与导航新方法[J].
机器人, 2006, 28(3): 275-278.
LI Yunchong, HE Kezhong. A novel obstacle avoidance and navigation method for outdoor mobile robot based on laser radar[J]. Robot, 2006, 28(3): 275-278. |
| [21] | DUDEK G, JENKIN M. Computational principles of mobile robotics[M]. 2nd ed. Cambridge: Cambridge University Press, 2010. |
| [22] | DESAI J P, OSTROWSKI J, KUMAR V. Controlling formations of multiple mobile robots[C]//Proceedings of 1998 IEEE International Conference on Robotics and Automation. Leuven, Belgium: IEEE, 1998, 4: 2864-2869. |
| [23] |
任立敏, 王伟东, 杜志江, 等. 障碍环境下多移动机器人动态优化队形变换[J].
机器人, 2013, 35(5): 535-543.
REN Limin, WANG Weidong, DU Zhijiang, et al. Dynamic and optimized formation switching for multiple mobile robots in obstacle environments[J]. Robot, 2013, 35(5): 535-543. |



