2. 四川长虹电器股份有限公司, 四川成都 610041
2. Sichuan Changhong Electric Co., Ltd., Chengdu 610041, China
哈希(Hash)函数,也叫杂凑函数,是密码学中最基本的模块之一,广泛应用于密码协议、数字签名、消息鉴别、完整性认证等领域。因此,它在密码学中扮演着极其重要的角色。
杂凑函数的目的是产生数据块的“指纹”,它可以对任意长度的信息产生定长的输出。这个变换过程软硬件均易于计算实现,但其逆向变换过程在计算上不可行,即具有单向性。出于安全性的考虑,杂凑函数还必须满足抗弱碰撞性和抗强碰撞性。1991年,Ron Rivest提出了MD5算法,这曾经是使用最为广泛的杂凑算法。从20世纪90年代年开始,美国国家标准与技术研究院(NIST)陆续公布了SHA系列[1],并通过公开竞赛方式征集SHA-3[2]。
中国国家密码管理局在2010年发布了SM3密码杂凑算法[3],该算法适用于商用密码中的多种应用,满足多种密码应用的安全需求:1)数字签名和验证,如作为SM2算法中数字签名所需的杂凑函数;2)消息认证码的生成与验证,消息认证码不仅可以使用分组密码算法基于特定的工作模式生成,也可以使用SM3等杂凑函数生成;3)随机数的生成。
哈希函数在各种平台和环境下的执行效率是非常重要的考量指标之一,比如服务器端常需执行的SSL/TLS协议就使用了哈希函数进行认证。目前已有大量文章对SHA系列算法的软件快速实现进行研究,比如Aciimez[4]提出基于SIMD技术快速实现哈希算法,Gueron等[5, 6]对并行处理多个消息的情况进行了研究。同样也有大量文章对SM3算法的软硬件快速实现进行研究。张倩等[7]提出了一种ASIC高效实现架构;王晓燕等[8]基于FPGA设计SM3算法IP核的整体架构,对关键逻辑进行优化设计;伍娟[9]以同方公司THD86智能卡芯片为硬件平台实现了SM3算法;曾小波等[10]分析了基于8051软核的SM3算法IP原理、设计流程及实现方案,该方案在时序和面积上均做到相当程度的优化,并提高了算法的效率;沈一公等[11]基于Android平台研究了SM3算法的快速实现,并以此为基础研究文件防篡改以便检查手机软件的安装;易叔贤等[12]结合已经将SM系列算法纳入其中的PBOC 3.0新规范,分析考虑SM2、SM3、SM4算法在金融IC卡领域的实现和应用。
与这些研究相比,文本研究的侧重点是SM3算法在普通软件平台下的快速实现方式。文本根据算法以及压缩函数的特点,给出一种更加适用于软件快速实现的算法描述方式和实现方法,本文提出的实现方法具有以下优点:首先,此方法避免了普通实现中可能采用的效率较低的实现架构和运算方式,可较大地提高算法的软件效率,经多个软件平台对比测试,本文的实现方法可将算法效率提升60%左右;其次,此方式不基于特定的软件平台、架构、指令等,具有很强的跨平台性和兼容性。
1 SM3算法简介SM3杂凑算法可将长度小于264比特的消息经过填充、反复的消息扩展和压缩,生成长度为256比特的杂凑值。在SM3算法中,字表示长度为32的比特串。
1.1 函数布尔函数FFi(X,Y,Z)、GGi(X,Y,Z),0≤i≤63的定义如下:
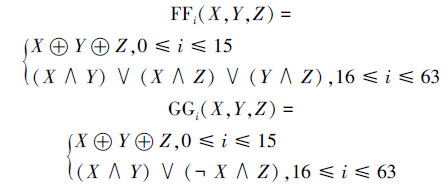
置换函数P0(X)和P1(X)的定义如下:
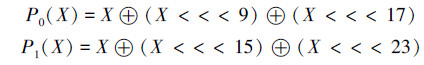
设消息的长度为l比特。填充方式为:首先将比特“1”添加到消息的末尾;然后添加k个“0”,k是满足l+1+k=448mod512的最小的非负整数;最后再将消息长度l的64位二进制表示添加在最末。填充后的消息比特长度为512的倍数。
1.3 迭代压缩填充后的消息m′按512 比特进行分组:m′=B(0)‖…‖B(n-1).对每个分组利用压缩函数CF进行迭代:
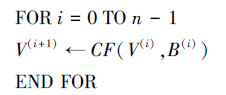
压缩函数CF的计算过程如下:
首先,计算消息扩展字Wi,0≤i≤67和Wi′,0≤i≤63,步骤如下:
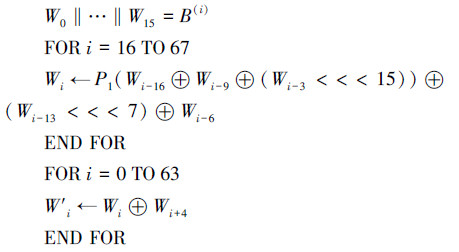
然后,进行包含64轮迭代的压缩,步骤如下:


256比特杂凑值y的计算方式为

从理论上讲,SM3算法中使用最多且最耗时的是64轮压缩函数和消息扩展。利用Intel VTune Amplifier XE分析算法热点,得出信息如下表。
| 参数 | 耗时/s | 百分比/% |
| 整体 | 21.795 | 100 |
| 压缩函数 | 14.355 | 65.9 |
| 消息扩展 | 5.287 | 24.3 |
| 其他 | 2.153 | 9.8 |
热点信息显示,压缩函数和消息扩展的确是最耗时的2个部分,其耗时分别占总耗时的65.9%和24.3%。因此,快速实现的关键在怎样快速实现压缩函数和消息扩展。
2.1 消息扩展的快速实现消息扩展的目的是利用512比特的消息分组B扩展得到68个字W0,…,W67和64个字W′0,…,W′63。
快速实现时,为了尽可能减少不必要的数据加载和存储,W0,…,W67和W′0,…,W′63的计算可以调整到压缩函数里执行,具体实施过程是:
1)首先在执行64轮压缩函数前只计算初始的4个字W0,…,W3;
2)然后在压缩函数的第i轮生成Wi+4,而W′i则使用W′i=Wi⊕Wi+4代替。
经过这样的调整,去掉了字W′0,…,W′63,减少了字W0,…,W67和W′0,…,W′63的加载和存储次数,提高了消息扩展的速度。
2.2 压缩函数的快速实现压缩函数的快速实现可以从结构调整、流程变更、常数计算等方面着手。
1)压缩函数的结构可以做适当的调整。压缩函数每一轮的最末会执行如下所示的循环右移,A‖B‖C‖D←(A‖B‖C‖D)>>>32,E‖F‖G‖H←(E‖F‖G‖H)>>>32。为了减少循环移位导致的不必要的赋值运算,可以将字的循环右移变更每轮输入字顺序的变动,且这个顺序变动会在4轮后还原,具体情况如下(以下用OneRound(·)表示一轮压缩):
OneRound(i+0,A,B,C,D,E,F,G,H,W)
OneRound(i+1,D,A,B,C,H,E,F,G,W)
OneRound(i+2,C,D,A,B,G,H,E,F,W)
OneRound(i+3,B,C,D,A,F,G,H,E,W)
2)可以优化压缩函数的中间变量的生成流程。此优化生成流程可以去除不必要的赋值,减少中间变量个数。优化后的执行步骤如下(其中ti=Ti<<<i为常数):
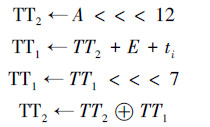
3)利用上述调整以及消息扩展部分的调整可以将原来计算TT1、TT2、D和H的过程进行如下的进一步简化。

4)预先计算并存储常数ti=Ti<<<i。这可以避免每个消息分组都去计算常数,且占用的存储空间也很少,仅256 Byte。
优化后的算法将消息扩展和压缩函数结合在一起。下面先描述调整后的消息处理算法,该算法完成消息扩展和64轮压缩迭代;再描述调整后的一轮算法,该算法完成一轮压缩迭代,包括计算必需的消息扩展字Wi+4。调整后的消息处理算法描述如下。
算法1 调整后的消息处理算法
ProcessBlock(V,M)
输入:上轮迭代结果V,一个消息分组B
输出:本轮迭代结果V
中间变量:字寄存器A—H,
步骤:
1)W0‖W1‖W2‖W3←B0‖B1‖B2‖B3,
2)A‖B‖C‖D‖E‖F‖G‖H←V,
3)FOR (i=0,4,8,…,60),
OneRound(i+0,A,B,C,D,E,F,G,H,W),
OneRound(i+1,D,A,B,C,H,E,F,G,W),
OneRound(i+2,C,D,A,B,G,H,E,F,W),
OneRound(i+3,B,C,D,A,F,G,H,E,W),
END FOR
4)V←V⊕(A‖B‖C‖D‖E‖F‖G‖H),
5)返回V。
对算法1做以下几点说明:这里的B0‖B1‖…‖B15=B分别代表消息的16个字;前4个消息扩展字W0、W1、W2、W3需在循环前计算出来,进入后面的循环后,每次执行OneRound(i,*)将计算Wi+4。
调整后的一轮压缩算法如下。
算法2 调整后的一轮压缩算法
OneRound(i,A,B,C,D,E,F,G,H,W)
输入:字寄存器A—H,轮序号i,消息扩展字数组W=(W0,…,W67)
输出:更新后的A—H和W=(W0,…,W67)
步骤:
1)计算消息扩展字Wi+4
IF(i < 12)Wi+4←Bi+4
ELSE Wi+4←P1(Wi-12Wi-5⊕(Wi+1<<<15))⊕(Wi-9<<<7)⊕Wi-2
END IF
2)计算中间变量TT1和TT2
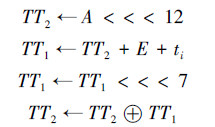
3)仅更新字寄存器B、D、F、H。
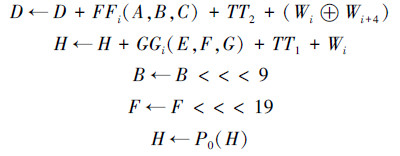
4)返回更新后的A—H和W=(W0,…,W67)。
对算法2做以下几点说明:进入第i轮的算法2之时,消息扩展字只有{Wk|k < i+4}这部分信息已经求出,执行完毕后Wi+4也被计算出来;步骤2中的ti为常量Ti<<<i,应预先计算并存储,使用时只需查表;由于Wi、FFi、GGi的计算方式在i < 16时和i≥16时不同,因此可以考虑将OneRound函数分为0≤i<12、12≤i<16、16≤i<643种情况分别实现。
3 2种实现方式的计算量分析评估为了从理论上评估新方法的效率,本节对2种方法的计算量进行详细对比。由于算法的操作主要集中在压缩函数中,因此以下对压缩函数的计算量进行统计、分析和对比。优化前的方法严格按照标准文档,先计算消息扩展字,再进行64轮迭代,优化后的方法则按照上一节描述的算法1和算法2进行实现。以下用LOAD和STORE表示数据加载和存储,XOR表示异或运算,ROT表示移位运算,ADD表示加法运算,AND表示与运算,OR表示或运算,NOT表示非运算。
优化前的算法中,消息扩展的计算量为:
1)计算前16个Wi时每个需执行1次LOAD和1次STORE,计算后52个Wi时每个需执行5次LOAD、1次STORE、6次XOR、4次ROT;
2)计算64个W′i每个需执行2次LOAD、1次STORE、1次ROT;
3)计算压缩函数的一次迭代需要执行3次LOAD、12次STORE、8次ADD、3次XOR、8次ROT、1次FFi函数和1次GGi函数,
4)FFi函数和GGi函数的计算量是,前16次FFi函数需执行2次XOR和2次ROT,前16次GGi函数需执行2次XOR和2次ROT,后48次FFi函数需执行3次AND和2次OR,后48次GGi函数需执行2次AND、1次OR、1次NOT。
根据以上统计分析,表 2列出了优化前的算法中对一个512 比特的消息块执行一次完整的压缩所需的计算量。
优化后的算法中,消息扩展的计算量为:
1)计算前12个Wi+4时每个需执行1次LOAD和1次STORE,计算后52个Wi+4时每个需执行5次LOAD、1次STORE、6次XOR、4次ROT;
2)计算中间变量TT1和TT2需要执行1次LOAD、2次STORE、2次ADD、1次XOR、2次ROT;
3)更新字寄存器B、D、F、H需要执行:1次LOAD、1次STORE、6次ADD、3次XOR、4次ROT、1次FFi函数和1次GGi函数;
4)FFi函数和GGi函数的计算量同优化前的计算量。
根据以上统计分析,表 2列出了优化后的算法中对一个512 比特的消息块执行一次完整的压缩所需的计算量。
| LOAD | STORE | ADD | XOR | ROT | AND | OR | NOT | 合计 | |
| 优化前 | 596 | 900 | 512 | 632 | 720 | 240 | 144 | 48 | 3 792 |
| 优化后 | 400 | 256 | 512 | 632 | 592 | 240 | 144 | 48 | 2 824 |
从表 2可知,优化后的压缩函数通过轮函数的调整和消息扩展函数的优化,大大减少了LOAD和STORE的次数,同时中间变量TT1和TT2的优化实现又进一步减少了ROT的次数,其余运算的计算量无变化。
如果从操作总数的角度考虑,优化后算法的速度可提升(3792-2824)/2824=34.3%。但实际上CPU执行这些操作指令时,不同的操作具有不同的指令执行周期(cycle),甚至不同的CPU执行相同的运算所需的指令周期也各不相同。大部分CPU执行整数的算数运算和逻辑运算需1个时钟周期,而执行LOAD和STORE则需要多个时钟周期,且各CPU的执行时间也有较大差异。以下假设执行每个算数逻辑运算需1个时钟周期。如果执行LOAD需1个时钟周期,执行STORE需2个时钟周期,则优化后算法的速度可提升52.3%。;如果假设执行LOAD需1.5个时钟周期,执行STORE需2.5个时钟周期,则优化后算法的速度可提升59.6%;如果假设执行LOAD需2个时钟周期,执行STORE需3个时钟周期,则优化后算法的速度可提升65.6%。不同假设下的速度提升情况见下表 3。
| 算数逻辑 运算(cycle) | LOAD (cycle) | STORE (cycle) | 速度 提升/% |
| 1 | 1.0 | 1.0 | 34.3 |
| 1 | 1.0 | 2.0 | 52.3 |
| 1 | 1.5 | 2.5 | 59.6 |
| 1 | 2.0 | 3.0 | 65.6 |
为了模拟真实环境中对SM3算法软件实现的需求,下面的实验中进行了4组测试,每组测试方法对多个数据包进行杂凑,每个数据包为特定长度字节,然后统计耗时和速度。以下为4组测试的详细情况说明。
1)第1组测试中测试1个数据包,该数据包为256×106个字节,此测试用以模拟大量数据杂凑的情况,如大型文件杂凑;
2)第2组测试中杂凑200个数据包,每个数据包1.28×106个字节,此测试用以模拟中型数据包杂凑的情况,如图片等;
3)第3组测试中杂凑40000个数据包,每个数据包6.4×103个字节,此测试用以模拟普通网络数据包杂凑的情况;
4)第4组测试中杂凑8×106个数据包,每个数据包32个字节,此测试用以模拟频繁的微小型数据包杂凑的情况。
为了统计每种测试的准确耗时值,每组测试都反复进行21次并记录各次的时间,最后从大到小排列后取最中间的值作为统计耗时值。
测试使用的软件平台详情如下:Windows XP SP3 32比特、Intel Core i3@3400 MHz、4 GB DDR3-1600 SDRAM、Microsoft Visual Studio 8.0。速度单位为Mbit/s。其中处理器的缓存情况为[13]:一级缓存为每个核心32KB,2级缓存为每个核心64KB,3级缓存为多核共享3MB。
| 测试 类别 | 速度/(Mb·s-1) | 速度 提升/% | |
| 优化前 | 优化后 | ||
| 第1组测试 | 739 | 1 203 | 62.8 |
| 第2组测试 | 733 | 1 191 | 62.5 |
| 第3组测试 | 701 | 1 074 | 53.2 |
| 第4组测试 | 642 | 973 | 51.6 |
| 平均 | 704 | 1 110 | 57.7 |
上表列出的测试结果表明:1)数据包越大,执行效率越高,这是因为大型数据包减少了一头一尾的初始化、消息填充和反初始化等工作:2)优化调整后的算法效率提升显著,可以提升60%左右,在杂凑大中型数据包时速度提升60%以上,即使在杂凑微小型数据包时效率也能提升50%以上。
4 结束语本文对我国国家密码管理局发布的SM3密码杂凑算的软件快速实现进行研究,根据算法自身的特点,尤其是压缩函数的特点,给出一种更加适用于软件快速实现的算法描述方式和实现方法。理论分析得出的算法计算量以及模拟实验结果均表明,利用此软件快速实现方法可以将算法的效率提升60%左右。另外,此软件快速实现方式不基于特定的平台、架构、指令等,因此具有很强的跨平台性和兼容性。
| [1] | NIST. Federal information processing standards publication 180-3, secure hash standards(SHS)[S]. Gaithersburg, MD, USA:Information Technology Laboratory of National Institute of Standards and Technology, 2008. http://csrc.nist.gov/publications. |
| [2] | NIST. Cryptographic hash algorithm competition.(2005-04-15). http://csrc.nist.gov/groups/ST/hash/sha-3/index.html. |
| [3] | 国家密码管理局. SM3密码杂凑算法[S]. 北京:国家密码管理局, 2010. National Cryptography Administration. SM3 cryptographic hash algorithm[S]. Beijing:National Cryptography Administration, 2010. |
| [4] | ACIICMEZ O. Fast hashing on pentium SIMD architecture[D]. Corvallis, Oregon:Oregon State University, 2004. |
| [5] | GUERON S, KRASNOV V. Parallelizing message schedules to accelerate the computations of hash functions[R]. 2012. http://eprint.iacr.org/2012/067.pdf |
| [6] | GUERON S, KRASNOV V. Simultaneous hashing of multiple messages[J]. Journal of Information Security, 2012, 3(4):319-325. |
| [7] | 张倩, 李树国. SM3杂凑算法的ASIC设计和实现[J]. 微电子学与计算机, 2014, 31(9):143-146, 152. ZHANG Qian, LI Shuguo. Design and implementation of SM3 algorithm in ASIC[J]. Microelectronics & Computer, 2014, 31(9):143-146, 152. |
| [8] | 王晓燕, 杨先文. 基于FPGA的SM3算法优化设计与实现[J]. 计算机工程, 2012, 38(6):244-246. WANG Xiaoyan, YANG Xianwen. Optimization design and implementation of SM3 algorithm based on FPGA[J]. Computer Engineering, 2012, 38(6):244-246. |
| [9] | 伍娟. 国密SM3算法在COS上的研究与实现[J]. 科技信息, 2013,(2):294-295. WU Juan. Research and implementation of SM3 algorithm on COS[J]. Science & Technology Information, 2013,(2):294-295. |
| [10] | 曾小波, 唐忠彪, 焦歆. 基于单片机的SM3算法优化及Verilog模型验证[J]. 电子科技, 2015, 28(2):38-40. ZENG Xiaobo, TANG Zhongbiao, JIAO Xin. Optimization of SM3 algorithm and Verilog model validation based on SCM[J]. Electronic Science and Technology, 2015, 28(2):38-40. |
| [11] | 沈一公, 苏厚勤. 基于Android的SM3密码杂凑算法研究与实现[J]. 电子技术与软件工程, 2013(18):69-70. SHEN Yigong, SU Houqin. Research and implementation of SM3 algorithm based on android[J]. Electronic Technology & Software Engineering, 2013(18):69-70. |
| [12] | 易叔贤, 张非凡. SM系列算法在金融IC卡领域的应用[J]. 金融电子化, 2013(7):49-52. YI Shuxian, ZHANG Feifan. Application of SM series algorithm in the field of financial IC card[J]. Financial Computerizing, 2013(7):49-52. |
| [13] | ntel. 2nd generation intel® coreTM processor family desktop datasheet.(2011-01-04). http://www.intel.com/content/www/us/en/processors/core/2nd-gen-core-desktop-vol-1-datasheet.html. |



