, ,
2. 浙江大学宁波理工学院, 浙江宁波 315000;
3. 浙江大学宁波理工学院, 浙江宁波 315000
, ,
2. Research Center on Intelligent Computing and Data Management Ningbo Institute of Technology, Zhejiang University, Ningbo 315000, China;
3. Research Center on Intelligent Computing and Data Management Ningbo Institute of Technology, Zhejiang University, Ningbo 315000, China
复杂网络作为刻画和研究复杂系统结构及其动态发展的强有力工具之一，近年来迅速成为学术界研究的热点，并与计算机科学、生物学、社会学、经济学等学科交叉融合，广泛应用于诸如生物网络、传染病控制、知识网络、电力网、互联网等各种自然和社会动态网络及系统研究中.复杂网络的研究涵盖很多方面，其中网络的演化及建模研究能够相当程度地揭示实际网络及系统的结构组成及变化规律，从而能够对系统的未来发展做出预测并提早设置改进措施。因此演化模型一直是复杂网络研究的热点之一，并提出了很多网络演化模型，以刻画现实中各种不同网络的特征及结构。
Watts等[1]提出小世界模型，具有短路径、高聚类和强传递性特征，模拟人际关系网络的演化过程。Barabási等[2]在研究万维网时提出基于增长和优先连接的无标度BA模型，连接概率与节点度成线性正比，较好地模拟出万维网中幂率度分布特征和马太效应。之后，研究者们发现幂率度分布特征广泛存在于各种现实网络，随着Falatous等[3]发现互联网拓扑的幂率特性，AB模型[4]被提出应用于互联网拓扑建模，其在BA模型基础上增加了内部连接和重配置过程；基于现实互联网连接倾向度更高的观测现象，广义线性优先模型[5]改进BA模型以模拟新节点连接对高度hub的优先选择性；动态优先模型[6]基于不同层级AS间的关系，反映出互联网中的小世界特性；多局域世界模型[7, 8]考虑节点连接的局域特征，能较好反映节点层次性和聚类性。众多研究表明，合作网络[9]、软件组件系统[10]、蛋白质网络[11]、在线社交网络[12]、传感器网络[13]等都呈现出了度分布幂率特性，局部事件模型被用来模拟软件组件系统的无标度特性；顶点复制模型[14]描述知识引用网络和新陈代谢网络，新节点不完全遵循优先连接机制，而是通过模仿已有节点来构建模型。
在线社交网络如微博、交友等是社会网络的一种典型关系网络，将每个用户看作网络节点，许多研究已经表明其节点度遵循幂率分布规律，但对于其结构演化模型方面的相关研究还比较少。一方面，目前研究集中于通过抽样数据来进行数据分析，从统计角度发现拓扑特征，虽然能较好还原真实网络特性，但这种研究属于静态分析，不能模拟动态过程以及添加行为过程；另一方面，研究表明在线社交网络节点可能比一般网络更倾向于连接度大的节点，很多传统模型不能直接适用，需要进行一定的改进。
本文提出一种在线社交网络演化模型，以注册用户作为网络节点，节点间的连边就是注册用户间的关注关系，节点和连边共同构成网络，不失一般性，本文将此网络抽象成无向网络图。演化模型考虑随机增长、优先连接、内部增长及连接更替4种机制，采用平均场理论对模型度分布进行理论分析。理论分析和仿真表明，演化模型网络的度呈现无尺度特征，且能够模拟较大范围的幂率分布，具有广泛的适用性，并能一定程度地模拟真实在线社交网络的度分布特征。
1 在线社交网络演化模型本文构造无向的网络演化模型，模拟了内部增长即网络中现有节点间添加新连接、内部调整即现有节点间重连接及网络增长即新节点和现有节点的连接等机制，对于有向网络亦可以参照文中分析。具体演化步骤如下：
1)初始化：初始网络包含m0个节点，每个节点与其余m0-1个节点相连；
2)随机增长：每个时间步添加一个新节点，并连接到m1个原有节点上，且满足m1 < m0；
3)优先连接：新节点与原有节点i相连接的概率Πi表达式为
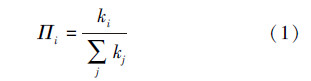
式中：ki为节点i的度；
4)内部随机增长：每个时间步在网络内增加m2条边，节点i被选为新增边的端点的概率Πi按式(1)计算，且 m2 < m0；
5)内部优先连接更替：每个时间步选择m3条边进行更替，更替方法为先随机选择节点i，随机移除与节点i相连的某条边lij，添加以连接节点j和节点r的边ljr，节点r按Πr概率择优选取，Πr按式(1)计算。
相比一般网络，在线社交网络中的连接度大的节点可能更容易得到大量连接，因此在演化模型中，除了新节点和内部增长具有优先连接机制外，内部优先连接更替也不同于一般模型中的重连机制，后者通常是以边lir替代lij，节点i的度不发生变化；而内部优先连接更替是以ljr替代lij，更加强化高连接度节点间的连接倾向，且为防止出现孤立节点，模型设定当被选择节点度为1时，进行重新选点。
2 演化模型的度分布属性 根据平均场理论对模型的度分布进行近似分析，假设节点度ki随时间t连续变化，对ki变化率求解：
随机增长：当新节点加入时，按概率Πi连接到m1个原节点上，则ki变化率方程为
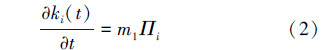
内部随机增长：边的端点按概率Πi优先选择，边有2个端点，则ki变化率方程为
内部优先连接更替：包含2个过程，首先是移除过程，节点i被随机选中的概率为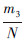
，N为节点总数，被选择为移除边的另一端的概率为m3Πi；其次是更替过程，被选择为更替边的两端的概率为2m3Πi，因此整个更替过程ki变化率方程为
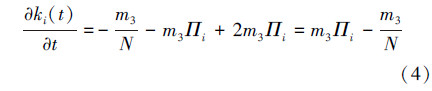
综合式(2)~(4)，得到演化模型ki变化率方程为
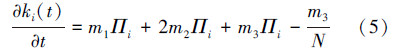
由网络节点平均度数为2(m1+ m2)，并且对于充分大的t，t时刻节点总数N为m0+t≈t，因此网络节点总度数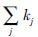
≈2(m1+m2)t，得
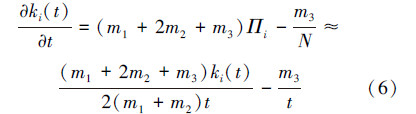
用变量分离法解此一阶微分方程可得
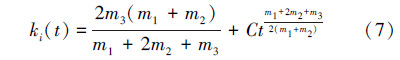
设节点i是在ti时刻进入网络，则有初始条件ki(ti)=m1，结合式(7)可得
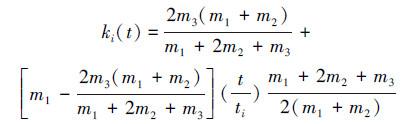
网络中节点i的度ki(t)小于k的概率为
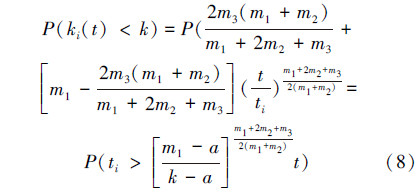
式中：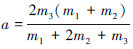
模型假设节点是以相对时间间隔进入网络的，因此节点i的到达时间ti具有常数概率密度：
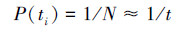
故有
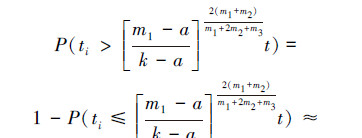
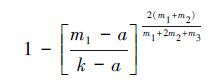
假设时间t→∞时，网络节点的度具有稳态分布P(k)：
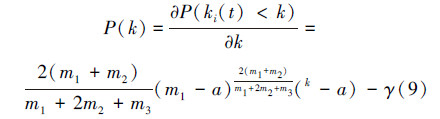
则度分布指数
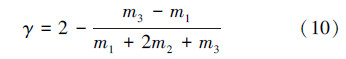
上述理论分析表明，由本演化模型生成的网络具有无标度特性，且通过调整m1、m2和m3的取值，能得到不同的分布指数。由－1≤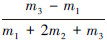
< 1，可得1 < γ≤3。当m2=m3=0时，γ=3，无标度BA模型成为本演化模型的一个特例。现有研究表明，绝大多数无标度网络的幂指数都在1~3，因此本演化模型具有广泛的适用性。
仿真实验分为2部分：1)采用MATLAB软件开发仿真程序，通过程序运行的结果来分析演化模型的度统计特性、相关参数的影响以及理论分析的准确性；2)通过MATLAB软件分析真实社交网络数据的度统计特性，观察演化模型理论分析值的模拟程度。
分析度分布指数γ的表达式(10)，可以看到3个参数的作用各不相同，m1和m3决定γ取值大于2或者小于2，m2则只影响值的大小，而m1和 m2又影响网络的节点规模和平均度数。图 1、2、3分别显示了1500节点网络演化模型在不同参数取值下的度分布情况，演化网络度分布呈现幂率特征，且根据参数取值的不同在1~3之间变化，图中直线由度分布理论表达式(9)近似给出。
 |
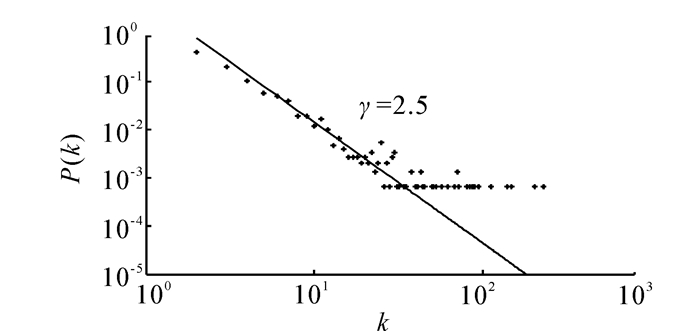| 图 1 演化模型度分布(m1=2,m2=1,m3=0)Fig. 1 Degree distribution of evolution model(m1=2 ，m2=1 ，m3=0) |
 |
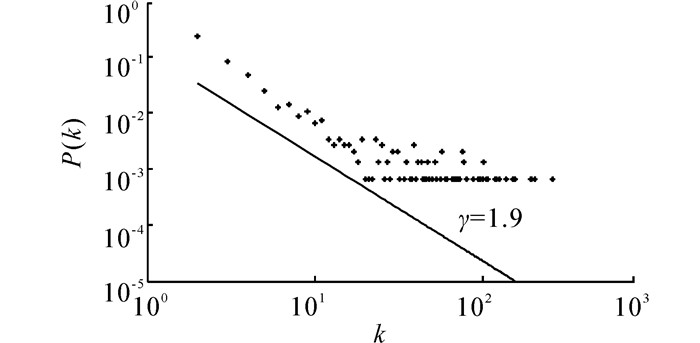| 图 2 演化模型度分布(m1=2，m2=1，m3=3)Fig. 2 Degree distribution of evolution model(m1=2，m2=1，m3=3) |
 |
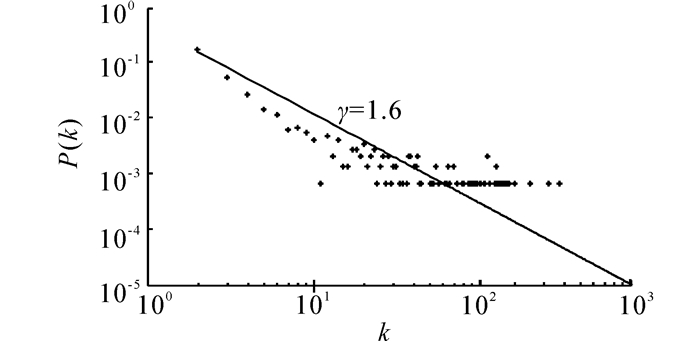| 图 3 演化模型度分布(m1=2，m2=1，m3=6)Fig. 3 Degree distribution of evolution model(m1=2，m2=1，m3=6) |
可以看到，在m1和m2值不变的条件下，m3值越大，无标度特性越大。图 4则显示在m1和 m3值不变的条件下，m2值变化对度分布幂率的影响，分布幂率值随着m2值变大而增大，但逐步接近某固定值，由式(10)可知，此值为2。
 |
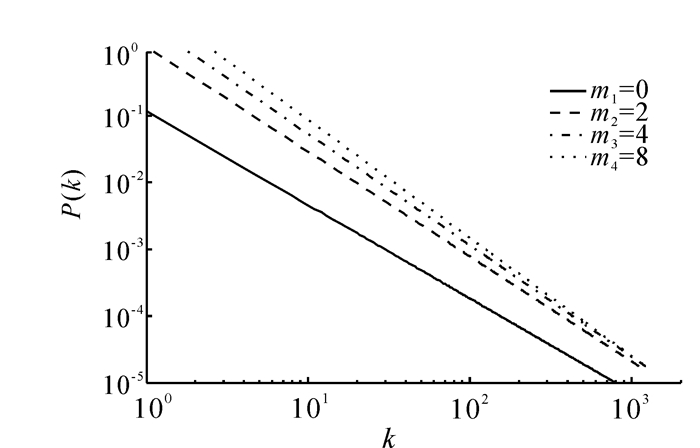| 图 4 m2取不同值时的度分布变化(m1=2，m3=8)Fig. 4 Degree distribution changes according to different values of m2 (m1=2，m3=8) |
采用真实在线社交网络与本文演化模型的度分布进行对比分析。图 5显示一个美国政治家博客用户网络[15]的度分布情况，该网络节点为博客网页，边表示为网页间的超链接，包含1224个节点和16714条无向边。可以看到，博客网页网络的度分布幂率在1~2，传统很多演化模型如BA及其变型模型的度分布幂率在2~3，不能较好地表征博客网络的度分布特征。图中拟合直线幂率值为1.4，由本文表达式(9)直接给出，其中参数取值m1=2、m2=0、m3=8，实际上有很多种参数取值方案，这里只给出其中一种仅用于说明效果。通过调整参数，演化模型能较好地模拟美国政治家博客用户网络的度分布特征。
 |
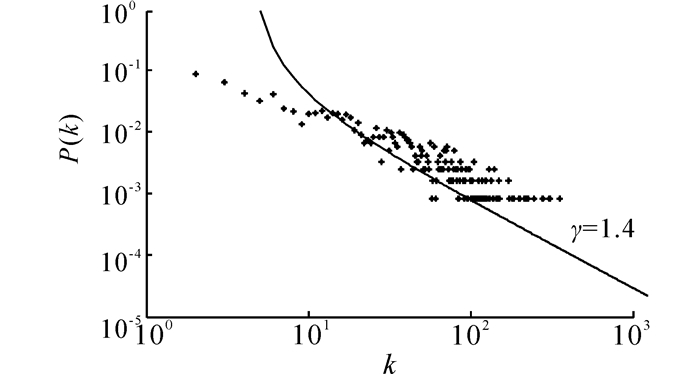| 图 5 政治家博客用户网络度分布幂率Fig. 5 Power-law degree distribution network of Political blogs |
图 6显示维基选举社交网络[15]度分布情况，该网络节点为维基用户，边表示为用户间的选举行为，包含7000多节点。该网络度分布幂率也在1~2之间，传统模型不能较准确地表征。图中拟合直线幂率值为1.5，由表达式(9)直接给出，其中参数取值m1=2、m2=0、m3=6，这里同样只给出一种取值方案用于说明效果。可以看到，通过调整参数，演化模型能较好地模拟维基选举社交网络的度分布特征。
 |
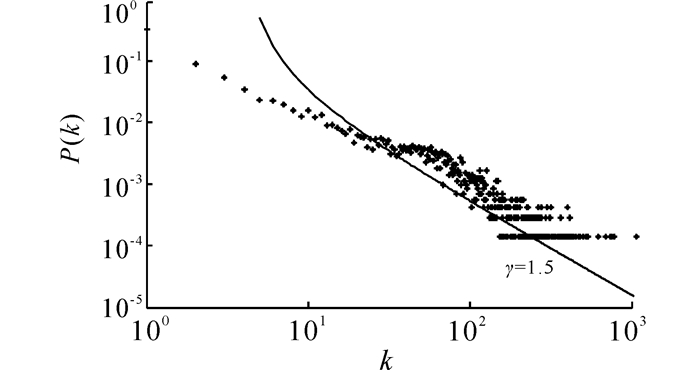| 图 6 维基选举社交网络度分布幂率Fig. 6 Power-law degree distribution of Wiki vote |
在线社交网络作为一种普遍存在的社会网络，已经引起广泛的研究并证实其具有无标度特性，但对其结构演化模型的研究相对较少。本文提出一种基于内增长、外增长及内部边更替的在线社交网络演化模型，其优先连接机制具有强化高连接度节点间的连接倾向的特征。理论分析和实验表明，该模型具有无标度特性，且通过调整参数的不同取值，度分布幂率指数在1~3，具有普遍适用性。通过和真实在线社交网络结构的模拟分析，本文提出的演化模型能较好地反映出在线社交网络的度分布特征，且能够刻画不同类型的社交网络，具有较强的实用意义。
本文演化模型是基于最基本的无向无权网络，下一步的工作考虑扩展到复杂的多属性异构网络，这些属性包括有向、权值、节点能力等。借助因素空间理论[16, 17]，将多属性异构网络映射成因素空间网络，网络节点映射成因素空间对象，使其更加贴近于现实网络，通过权变、拓扑结构、动态时空等因素空间理论工具研究演化网络模型和实际在线社会网络的生成、发展及其特征。
| [1] | WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684):440-442. |
| [2] | BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439):509-512. |
| [3] | FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On power-law relationships of the Internet topology[J]. ACM SIGCOMM Computer Communication Review Homepage, 1999, 29(4):251-262. |
| [4] | ALBERT R, BARABASI A L. Topology of evolving networks:local events and universality[J]. Physical Review Letters 2000, 85(24):5234-5237. |
| [5] | BU T, TOWSLEY D. On distinguishing between Internet power law topology generators[C]//Proceedings of INFOCOM 2002. Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies. New York, NY:IEEE, 2002, 2:638-647. |
| [6] | PARK S T, PENNOCK D M, GILES C L. Comparing static and dynamic measurements and models of the Internet's as topology[C]//Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies. Hong Kong:IEEE, 2004, 3:1616-1627. |
| [7] | CHEN Guangrong, FAN Zhenping, LI Xiang. Modeling the complex Internet topology[C]//KOCAREV L, VATTAY G. Complex Dynamics in Communication Networks. Berlin Heidelberg:Springer, 2005. |
| [8] | 田思, 李慧嘉, 赵岳. 一种新型多局域世界网络模型分析[J]. 计算机应用研究, 2013, 30(3):869-872. TIAN Si, LI Huijia, ZHAO Yue. Analysis of novel multi-local world network model[J]. Application Research of Computers, 2013, 30(3):869-872. |
| [9] | NEWMAN M E J. The structure of scientific collaboration networks[C]. Proceedings of National Academy Sciences, 2001, 98(2):404-409. |
| [10] | MYERS C R. Software systems as complex networks:structure, function, and evolvability of software collaboration graphs[J]. Physical Review E, 2003, 68(4Pt2):046116. |
| [11] | JEONG H, MASON S P, BARABASI A L, et al. Lethality and centrality in protein networks[J]. Nature, 2001, 411(6833):41-42. |
| [12] | 王亚奇, 王静, 杨海滨. 基于复杂网络理论的微博用户关系网络演化模型研究[J]. 物理学报, 2014, 63(20):208902. WANG Yaqi, WANG Jing, YANG Haibin. An evolution model of microblog user relationship networks based on complex network theory[J]. Acta Physica Sinica, 2014, 63(20):208902. |
| [13] | 刘浩然, 尹文晓, 董明如, 等. 一种强容侵能力的无线传感器网络无标度拓扑模型研究[J]. 物理学报, 2014, 63(9):090503. LIU Haoran, YIN Wenxiao, DONG Mingru, et al. Study on the scale-free topology model with strong intrusion-tolerance ability in wireless sensor networks[J]. Acta Physica Sinica, 2014, 63(9):090503. |
| [14] | SOLE R V, PASTOR-SATORRAS R, SMITH E, et al. A model of large-scale proteome evolution[J]. Advances in Complex Systems, 2002, 5(1):43-54. |
| [15] | 维基选举社交网络..http://www.linkprediction.org/index.php/link/resource/data. |
| [16] | 汪培庄. 因素空间与因素库[J]. 辽宁工程技术大学学报:自然科学版, 2013, 32(10):1297-1304. WANG Peizhuang. Factor spaces and factor data-bases[J]. Journal of Liaoning Technical University:Natural Science, 2013, 32(10):1297-1304. |
| [17] | 汪培庄. 因素空间与数据科学[J]. 辽宁工程技术大学学报:自然科学版, 2015, 34(2):273-280. WANG Peizhuang. Factor spaces and data science[J]. Journal of Liaoning Technical University:Natural Science, 2015, 34(2):273-280. |