自1965年Zadeh首次提出模糊集[1]的概念以来,Zadeh本人以及其他一些学者相继给出了模糊集的一些推广形式。其中Atanassov将模糊集推广到了直觉模糊集[2]以及区间直觉模糊集[3],Zadeh等将普通模糊集推广到二型模糊集[4, 5]。随着信息技术的发展,Pawlak于1982年提出了粗糙集[6]的概念,由于模糊集和粗糙集理论在处理不确定性和不精确性问题方面都推广了经典集合论,因此将2个理论相融合,建立模糊粗糙集成为信息领域研究的主要方向之一。许多学者致力于这方面的研究,分别给出了模糊粗糙集[7]、直觉模糊粗糙集[8, 9]等概念。目前,一型广义模糊粗糙集理论的发展已达到了一个相对完善的状态。近年来,人们开始着手将模糊粗糙集理论进一步推广到二型模糊粗糙集[10],与此同时,二型模糊集的概念也被扩展到了二型直觉模糊集[11]。然而,关于二型直觉模糊集和粗糙集理论相融合的研究目前尚未见到,基于此,本文在二型模糊粗糙集理论的基础上,利用二型直觉模糊集和二型直觉模糊关系,将文献[10]中给出的二型模糊粗糙集模型进一步推广到二型直觉模糊粗糙集模型,同时还讨论了一些相关的性质。
1 二型直觉模糊集的基本理论定义1[11] 二型直觉模糊集。设U为论域,称A={〈x,μA(x),vA(x)〉|x∈U}为U上的一个二型直觉模糊集。其中
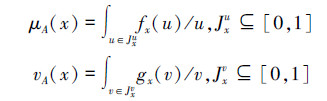
且对∀x∈U满足

μA(x)表示x对A的隶属程度,vA(x)表示x对A的非隶属程度。
为叙述方便,将μA(x)和vA(x)分别称为二型直觉模糊集的主隶属度和主非隶属度。
定义2[11] 二型直觉模糊集的基本运算。设A、B是论域U上的2个二型直觉模糊集,令

其中
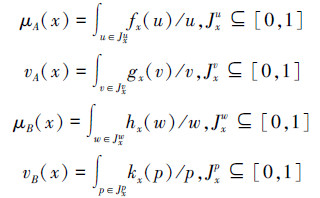
定义运算如下:
1)A∩B={〈x,μA∩B(x),vA∩B(x)〉|x∈U},
其中
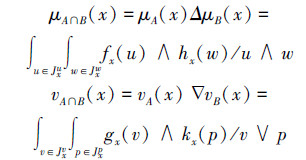
2)A∪B={〈x,μA∪B(x),vA∪B(x)〉|x∈U},
其中
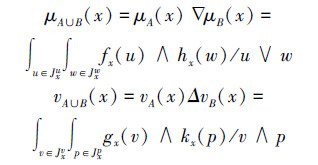
3)Ac={〈x,vA(x),μA(x)〉|x∈U}。
定理1 [11] 设A,B,C是论域U上的3个二型直觉模糊集,则下列各式成立:
1)交换律,A∪B=B∪A,A∩B=B∩A;
2)结合律,A∪(B∪C)=(A∪B)∪C,A∩(B∩C)=(A∩B)∩C;
3)幂等律,A∪A=A,A∩A=A;
4)对合律,(Ac)c=A;
5)德摩根律,(A∪B)c=Ac∩Bc,(A∩B)c=Ac∪Bc。
一般地,分配律和吸收律不成立。如果限定所有二型直觉模糊集的主隶属度和主非隶属度均为标准的凸一型模糊集,那么,分配律和吸收律便成立[10]。
定义3[11] 二型直觉模糊关系。设U和W是有限非空论域,定义在直积空间U×W上的二型直觉模糊子集称为从U到W的二型直觉模糊关系。记为
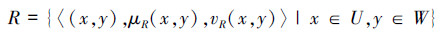
其中

且对∀(x,y)∈U×W,满足
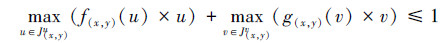
特别地,当U=W时,二型直觉模糊关系R称为U×U上的二型直觉模糊关系。
2 二型直觉模糊粗糙集及其性质定义4 设R是U×U上的二型直觉模糊关系,称(U,R)是二型直觉模糊近似空间,A是论域U上的一个二型直觉模糊集,A关于近似空间(U,R)的上近似和下近似分别是定义在U上的二型直觉模糊集,具体形式如下

其中
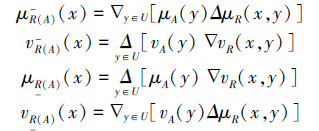
称(R(A)、R(A))为A关于(U,R)的二型直觉模糊粗糙集。
下面讨论特殊情况下的模型形式。
1)当R退化为U×U上的普通二型模糊关系,A退化为U上的普通二型模糊集时,定义4中的二型直觉模糊粗糙集退化为文献[10]中的二型模糊粗糙集。
这是因为,对∀x,y∈U,此时有
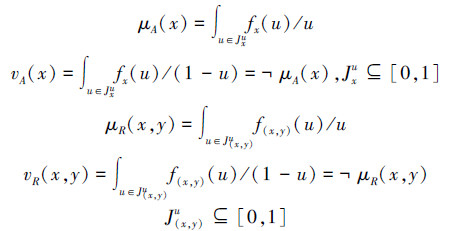
且由文献[12]可知下式成立:
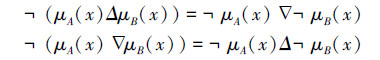
从而有
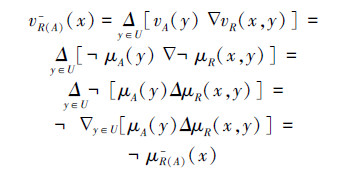
即
 为普通二型模糊集。
为普通二型模糊集。
同理可得
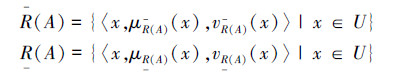 为普通二型模糊集。
为普通二型模糊集。
于是(R(A),R(A))为A关于(U,R)的普通二型模糊粗糙集。由此可见,本文给出的二型直觉模糊粗糙集是文献[10]中的二型模糊粗糙集的推广。
2)当R退化为U×U上的等价关系,A为U上的二型直觉模糊集时,定义4中的二型直觉模糊粗糙集退化为如下形式:
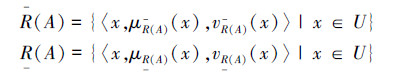
其中
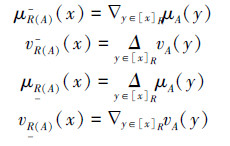
称(R(A),R(A))为A关于(U,R)的粗糙二型直觉模糊集。
下面讨论定义4中的二型直觉模糊粗糙近似算子的性质。为此先将文献[12, 13]中有关普通二型模糊集之间包含关系的定义推广到二型直觉模糊集。
定义5 设A、B是论域U上的2个二型直觉模糊集,规定
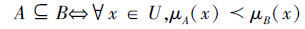
且vA(x) vB(x),其中序关系
vB(x),其中序关系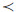 ,
, 定义为
定义为
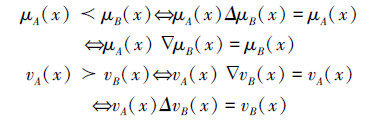
定义5中的的序关系具有如下性质。
定理2 设A,B,C是论域U上的3个二型直觉模糊集,若A⊆B,即∀x∈U,μA(x)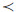 μB(x)且vA(x)
μB(x)且vA(x) vB(x)。则有下式成立:
vB(x)。则有下式成立:

证明 由定义5可直接验证。
定理3 设R和R是定义4中的上、下近似算子,A、B是论域U上的2个二型直觉模糊集,则有下列性质:
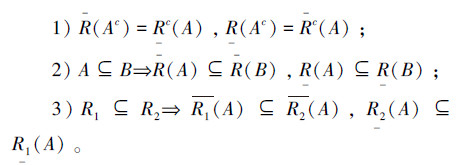
证明 1)因为
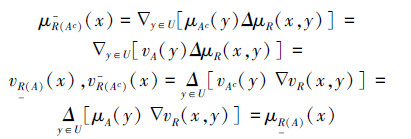
所以

同理可得:R(Ac)=Rc(A)。
2)若A⊆B,即 ∀x∈U,μA(x)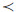 μB(x)且vA(x)
μB(x)且vA(x) vB(x),则有
vB(x),则有
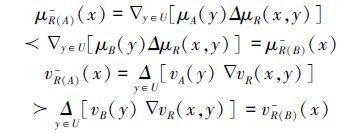
所以,R(A)⊆R(B)。同理可得:R(A)⊆R(B)。
3)若R1⊆R2,即 ∀ x∈U,
μR1(x,y)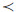 μR2(x,y)且vR1(x,y)
μR2(x,y)且vR1(x,y) vR2(x,y),那么有
vR2(x,y),那么有
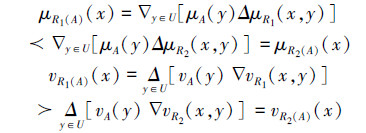
所以,R1(A)⊆R2(A)。
同理可得:R2(A)R1(A)。
需要指出的是,由于上文中研究的二型直觉模糊集的运算不满足分配律和吸收律,导致二型直觉模糊近似算子的一些性质不成立。例如
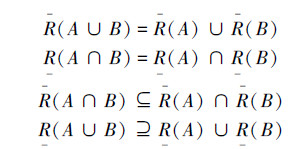
都不成立。如果限定所有二型直觉模糊集的主隶属度和主非隶属度均为标准的凸一型模糊集,那么上述性质便成立,其原因是:上述性质的证明过程需要使用分配律和吸收律。
为了便于研究和计算,假设下文中讨论的所有二型直觉模糊集都满足如下条件:主隶属度和主非隶属度都是标准的凸一型模糊集。
定理4 设R和R是定义4中的上、下近似算子,A、B是论域U上的2个二型直觉模糊集,则有下列性质:
1)R(A∪B)=R(A)∪R(B),
R(A∩B)=R(A)∩R(B);
2)R(A∩B)R(A)∩R(B),
R(A∪B)R(A)∪R(B)。
证明 1)对于 ∀x∈U,有
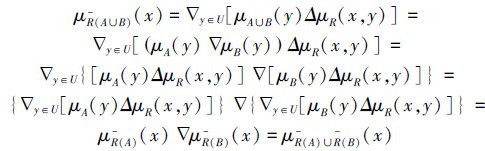
类似地,有

所以,R(A∪B)=R(A)∪R(B)。
同理可得:R(A∩B)=R(A)∩R(B)。
4)因为A∩B⊆A,B,由定理3的性质(2)有

所以,R(A∩B)R(A)∩R(B)。
同理可得:R(A∪B)R(A)∪R(B)。
3 二型直觉模糊关系与近似算子的特征联系定义6 设R是论域U×U上的二型直觉模糊关系,规定
1)R是自反的⇔x∈U,μR(x,x)=1/1且vR(x,x)=1/0。2)R是对称的⇔x,y∈U,μR(x,y)=μR(y,x)且vR(x,y)=vR(y,x)。
3)R是传递的⇔ ∀x,y,z∈U,∇y∈U[μR(x,y)ΔμRy,z)]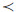 μR(x,z)
μR(x,z)
且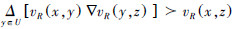 。
。
定义7 对于 ∀y∈U,二型单值直觉模糊集1y和其补集1U-{y}分别定义如下:
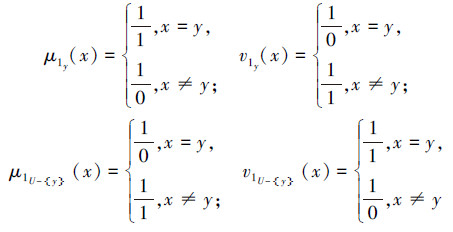
定理5 设(U,R)是一个二型直觉模糊近似空间,A是论域U上的一个二型直觉模糊集,则下列性质成立:
1)若R是自反的,则R(A)⊆A⊆R(A)。
2)若R是对称的,则 ∀x,y∈U,μR(1x)(y)=μR(1y)(x),vR(1x)(y)=vR(1y)(x),μR(1U-y)(x)=μR(1U-x)(y),vR(1U-y)(x)=vR(1X-x)(y)。
3)若R是传递的,则R(R(A))⊆R(A),R(A)⊆R(R(A))。
证明 1)若R是自反的,则 ∀x∈U,μR(x,x)=1/1且vR(x,x)=1/0。
那么有

并且

所以,R(A)⊆A。同理可得:A⊆R(A)。
即R(A)⊆A⊆R(A)。
2)若R是对称的,则 ∀x,y∈U,μR(x,y)=μR(y,x)且vR(x,y)=vR(y,x)。
那么有

类似地,有μR(1y)(x)=∇t∈U[μ1y(t)ΔμR(x,t)]=μR(x,y),所以,μR(1x)(y)=μR(1y)(x)。
同理可得
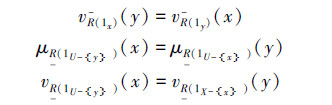
3)若R是传递的,则 ∀x,y,z∈U,∇y∈U[μR(x,y)ΔμR(y,z)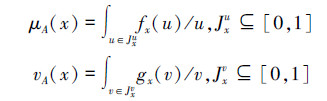 μR(x,z)。
μR(x,z)。
且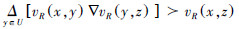 。
。
那么有
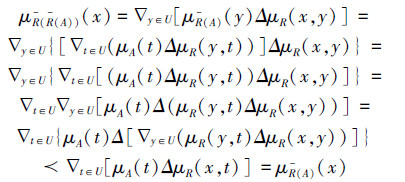
类似地,有

所以,R(R(A))⊆R(A)。
同理可得:R(A)⊆R(R(A))
4 结束语由于二型模糊系统具有较强的鲁棒性,在鲁棒控制、信号处理和系统辨识领域具有广泛的应用前景,因此将二型模糊集与粗糙集融合建模无疑具有理论意义和实际价值。直觉模糊集因其在对问题的描述上比模糊集更细腻,成为模糊集的自然推广,因此二型直觉模糊集与粗糙集的融合在实际应用中将会有更好地效果。本文将二型直觉模糊集和粗糙集相融合,建立二型直觉模糊粗糙集模型,同时给出了上、下近似算子的一些性质,为二型直觉模糊信息系统的约简奠定了基础,也为二型直觉模糊信息系统的应用提供了理论保障。
| [1] | ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3):338-353. |
| [2] | ATANASSOV K T. Intuitionstic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1):87-96. |
| [3] | ATANASSOV K T, GARGOV G. Interval valued intuitionstic fuzzy sets[J]. Fuzzy Sets and Systems, 1989, 31(3):343-349. |
| [4] | ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning[J]. Information Science, 1975, 8(3):199-249. |
| [5] | MENDEL J M, JOHN R I B. Type-2 fuzzy sets made simple[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(2):117-127. |
| [6] | PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5):341-356. |
| [7] | DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International Journal of General Systems, 1990, 17(2-3):191-209. |
| [8] | CORNELIS C, DE COCK M, KERRE E E. Intuitionistic fuzzy rough sets:at the crossroads of imperfect knowledge[J]. Expert Systems, 2003, 20(5):260-270. |
| [9] | ZHOU Lei, WU Weizhi. On generalized intuitionistic fuzzy rough approximation operators[J]. Information Sciences, 2008, 178(11):2448-2465. |
| [10] | 赵涛, 肖建. 二型模糊粗糙集[J]. 控制与决策, 2013, 28(3):385-390. ZHAO Tao, XIAO Jian. Type-2 fuzzy rough sets[J]. Control and Decision, 2013, 28(3):385-390. |
| [11] | 赵涛, 肖建. 二型直觉模糊集[J]. 控制理论与应用, 2012, 29(9):1215-1222. ZHAO Tao, XIAO Jian. Type-2 intuitionistic fuzzy sets[J]. Control Theory & Applications, 2012, 29(9):1215-1222. |
| [12] | KARNIK N N, MENDEL J M. Operations on type-2 fuzzy sets[J]. Fuzzy Sets and Systems, 2001, 122(2):327-348. |
| [13] | MIZUMOTO M, TANAKA K. Some properties of fuzzy sets of type2[J]. Information and Control, 1976, 31(4):312-340. |
| [14] | 邓廷权, 王占江, 汪培培, 等. 二型模糊集的模糊熵研究[J]. 控制与决策, 2012, 27(3):408-412. DENG Tingquan, WANG Zhanjiang, WANG Peipei, et al. Study on fuzzy entropy of type-2 fuzzy sets[J]. Control and Decision, 2012, 27(3):408-412. |



