遥感图像分类是遥感图像处理系统的核心功能之一,它实现了将图像中每个像元根据其在不同波段的光谱亮度、空间结构特征或者其他信息,按照某种规则或算法划分为不同的类别[1],是遥感 研究领域里的一项重要内容[2],遥感图像分类方法主要有监督和非监督分类法[3, 4]。随着遥感图像分类方法的发展,最大似然法、光谱角填图、支持向量机、匹配滤波、神经网络等方法已经在遥感图像分类及湿地信息提取中得到应用[5]。
国内外很多学者研究了利用粒子群优化算法对遥感图像进行分类。文献[1] 利用混合PSO-FCM算法和非监督学习动态聚类算法分别对湖南东洞庭湖3个主成分合成图像,进行湿地分类实验。文献[4]提出了一种基于粒子群算法和最近邻原则的高光谱图像半监督分类方法。文献[6]提出了基于自适应最优神经网络拓扑结构的多目标PSO算法的多光谱卫星图像的分类。基于量子粒子群优化算法的遥感图像分类的文献几乎没有。
Sun等[7]提出了QPSO算法,提高了粒子群的全局收敛能力。QPSO算法的思想来源于量子力学和PSO模型。它能保证算法的全局收敛并且在优化模型中只有位置向量,没有速度向量,控制参数少、寻优能力强。因此本文使用QPSO算法进行遥感图像的分类。但是QPSO算法像其他进化算法一样,也会遇到早熟收敛的问题,并且在收敛的后期粒子的多样性减少了,因此出现了许多改进的QPSO算法。Coelho[8] 介绍了基于Gaussian 概率分布的QPSO算法,在此算法中引入了变异算子;在QPSO算法中引入多精英模型来提高算法的收敛速度[9]。
因此在下面的分类过程中将使用一种多样性变异的机制防止QPSO算法的早熟收敛。本文结合QPSO算法和多样性变异对遥感图像进行分类。
2 研究方法 2.1 QPSO算法在一个D维的目标搜索空间中,QPSO算法有M个代表优化问题的一个可行解,即M为种群的粒子数,对于第i个粒子,在搜索空间的当前位置记为Xi=[xi1 xi2 … xiD],粒子没有速度向量。在算法的每一次迭代过程中,每个粒子当前经历的个体最好位置表示为pbesti=[pbesti1 pbesti2 … pbestiD]群体全局最好的位置表示为gbest=[gbest1 gbest2 … gbestD。
Clerc 和Kennedy对粒子轨道的分析中证明了这样一个事实:假如每一个粒子收敛到它的局部吸引点Ai=Ai1 Ai2 … AiD]并且满足条件(1),那么PSO算法是收敛的。
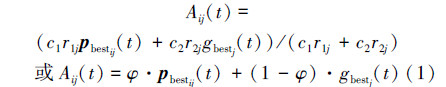
式中:j=1,2,…,D,φ=c1r1/(c1r1+c2r2),r1和r2为2个在(0,1)内均匀分布的随机数序列,c1和c2为PSO算法的加速因此,在通常情况下c1=c2。因此φj为一个在(0,1)内均匀分布的随机数序列。并且,从式(1)中可以看出局部吸引点Ai 是一个位于超矩形中的随机点。
下面介绍QPSO算法:
假如粒子在以吸引点为中心的一维δ势阱中运动,解一维δ势阱的Schrdinger 方程,得到概率分布函数为

式中:L为Delta势阱的特征长度,它决定了粒子的搜索范围。使用Monte Carlo方法,可得到粒子位置的进化公式为
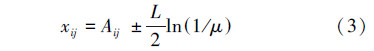
式中:μ为(0,1)内均匀分布的随机数,由于L的控制方法对QPSO算法的收敛速度和性能有关键性的影响,Sun在QPSO算法中引入了平均最好位置Cbest[6, 7],Cbest定义为所有粒子个体最好位置的平均值,即

L的值用式(5)计算,采用xij和Cbestj之间的间隔:
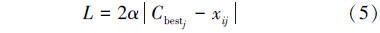
则式(3)的粒子位置更新方程为
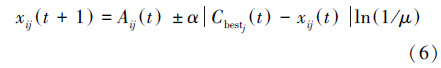
式中:参数∞为收缩-扩张系数,它是QPSO收敛的一个重要的参数,可以通过调节α的值来控制算法的收敛速度,其中α必定小于1.782来保证粒子的收敛[10],可取α=(1.0-0.5)× +0.5,可以达到比较好的效果。其中MAXITER为算法迭代的次数。
+0.5,可以达到比较好的效果。其中MAXITER为算法迭代的次数。
QPSO算法在搜索开始时,由于粒子群的初始化,多样性相对性比较高,在搜索的过程中,由于粒子的逐渐收敛,群体的多样性不断下降,在搜索的后期,由于粒子都聚集到一个相对较小的区间,粒子群的多样性已经很低,全局搜索能力已经变得很弱,进行大范围的搜索的能力已经很小,此时算法就会发生早熟现象。为了进一步改善QPSO算法的性能,本文受Ursem[11]和Right[12]的启发,在QPSO算法中引入多样性控制的方法(diversity-mutaion QPSO,DMQPSO),粒子群的多样性也采用粒子到中心点的平均欧几里德几何距离来度量,在QPSO算法中,存在粒子的个体最好位置组成的群体,因此QPSO算法的多样性度量采用如式(7)的形式:

式中: ,丨A丨为搜索空间中最长对角的长度。如果dt减小到dl之下,则执行变异操作:
,丨A丨为搜索空间中最长对角的长度。如果dt减小到dl之下,则执行变异操作:
对于每一个j,使
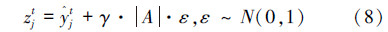
然后使ŷjt=zjt ,yg,jt =zjt 。这里yg,jt 表示全局最优位置的粒子的个体最优位置;N(0,1)代表标准正态分布;γ为用户指定的参数,必须大于dl,所以在变异之后dt才能及时增加到dl之上,假设γ≥10dl;zt是一个临时向量。当执行突变操作时,全局最优位置的粒子的偏移使丨ŷtj-yi,jt 丨的值增大并且把平均最优位置C拉离它原始的位置,使粒子的搜索范围扩大,并且每一次都导致dt值的增大。
2.3 基于DMQPSO的分类算法DMQPSO分类算法用于多光谱遥感图像分类是根据图像中的像素到每个聚类中心的距离,对目标函数进行迭代优化以确定最佳聚类。多光谱遥感对象象素组成M个样本集合X=(x1,x2,…,xM),用向量W=(w1,w2,…,wc)表示聚类中心的集合,c为聚类中心的个数,作为DMQPSO算法中的一个粒子。并且Xi和Wi的维度相同。数据向量到中心向量的距离用式(9)来计算:
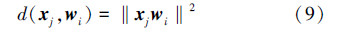
在DMQPSO算法分类过程中用到的目标函数为

分类算法的具体过程如下:
1)初始化粒子群W1,W2,…,Wc,作为第1代粒子群;
2)设置聚类类别数,多光谱遥感图像的波段数,终止条件的最大迭代次数;
3)根据式(10)计算多光谱遥感图像像素的适应度函数值;
4)根据式(4)计算平均最好位置Cbest
5)根据式(7)计算dt。IF dt<dl,则执行6),否则执行10);
6)根据式(8)对ŷjt和yg,jt执行变异操作
7)更新局部最优pbest;
8)更新全局最优gbest;
9)根据式(1)计算随机点;
10)根据式(6)更新粒子位置,产生下一代粒子群;
重复计算3)~10),直到满足迭代的次数。
3 仿真结果及分析 3.1 仿真数据实验平台为Intel Core(TM) i5-2450M 2.5 GHz处理器,4GB内存,Windows 7 操作系统,在MATLAB环境下编制DMQPSO的遥感图像分类程序。仿真数据来自ALOS多光谱遥感图像,其有8种主要地物类型:草地、林地、耕地、水体、居民区、裸土地、机场、道路。
3.2 参数设置在QPSO和DMQPSO算法的实现过程中,粒子数为30,最大迭代次数MAXITER 取值为200,收缩-扩张系α=(1.0-0.5)*(MAXITER-T)/MAXITER+0.5,聚类类别数为8,多光谱遥感图像波段数为3。在K-Means、QPSO和DMQPSO算法中聚类中心的个数为30。
3.3 遥感图像分类结果图本文分别使用DMQPSO、QPSO算法以及利用ENVI遥感图像处理软件的无监督分类模块的K-Means,对实验数据进行分类,得到分类结果如图 1。
 |
| 图 1 3种算法的遥感图像分类图Fig. 1 Sensing image classification produced by three algorithms |
从分类结果中可以看出:K-Means算法的分类结果中,草地和林地的混分现象比较明显,耕地、裸土地和道路也存在一定的混分现象,草地和水体也存在一些分类错误。QPSO算法在草地和林地上存在着混分现象,草地面积增大,水体和草地也有少量的混分。相对而言,DMQPSO算法能得到较好的分类,与原始遥感图像的视觉效果大概一致,但是草地和林地也存在少量的混分现象。
3.4 遥感图像的精度评价本文采用2种方法对分类结果进行精度评价:
1)像素级的评价
以分类后的混淆矩阵为基础,分别计算总体分类精度、Kappa系数、制图精度和用户精度。混淆矩阵是通过将每个地表真实像元的位置和分类与分类图像中相应位置和分类图像比较计算,混淆矩阵的每一列代表了一个地表真实分类,每一列中的数值等于地表真实像元在分类图像中对应于相应类别的数量。在实验过程中,树林、草地、房屋、道路、湖泊、土地的感兴趣区都随机选取800个数据。表 1给出了DMQPSO算法的混淆矩阵,QPSO和K-Means算法的感兴趣区与DMQPSO算法相同。
| 类别 | 草地 | 林地 | 耕地 | 水体 | 居民 区 | 裸土 地 | 机场 | 道路 | 行总 数 |
| 草地 | 620 | 121 | 50 | 65 | 35 | 58 | 29 | 15 | 993 |
| 林地 | 70 | 561 | 65 | 58 | 25 | 35 | 33 | 28 | 875 |
| 耕地 | 20 | 25 | 496 | 30 | 20 | 22 | 27 | 51 | 691 |
| 水体 | 5 | 33 | 28 | 480 | 18 | 20 | 32 | 34 | 650 |
| 居民区 | 26 | 26 | 22 | 32 | 625 | 15 | 38 | 88 | 872 |
| 裸土地 | 42 | 17 | 90 | 60 | 35 | 380 | 147 | 96 | 867 |
| 机场 | 12 | 10 | 24 | 45 | 30 | 20 | 358 | 156 | 655 |
| 道路 | 5 | 7 | 25 | 30 | 12 | 250 | 136 | 332 | 797 |
| 列总数 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 |
表 2给出了3种算法的像素级评价结果。从总体分类精度和Kappa系数来说,DMQPSO分类结果精度最高;从用户精度和制图精度来说,DMQPSO算法和QPSO算法的分类精度都比K-Means算法的分类精度高,总体上来说DMQPSO算法的分类精度稍高于QPSO算法。
| 样本 类别 | DMQPSO | QPSO | K-Means | |||||||||
| 用户 精度 | 制图 精度 | 总体分 类精度 | Kappa 系数 | 用户 精度 | 制图 精度 | 总体分 类精度 | Kappa 系数 | 用户 精度 | 制图 精度 | 总体分 类精度 | Kappa 系数 | |
| 草地 | 95 | 92 | 88.52 | 80.94 | 94 | 88 | 82.37 | 73.68 | 86 | 85 | 77.52 | 68.49 |
| 林地 | 93 | 90 | 88.52 | 80.94 | 90 | 82 | 82.37 | 73.68 | 77 | 81 | 77.52 | 68.49 |
| 耕地 | 91 | 88 | 88.52 | 80.94 | 91 | 87 | 82.37 | 73.68 | 87 | 78 | 77.52 | 68.49 |
| 水体 | 90 | 90 | 88.52 | 80.94 | 90 | 84 | 82.37 | 73.68 | 78 | 71 | 77.52 | 68.49 |
| 居民区 | 88 | 82 | 88.52 | 80.94 | 85 | 75 | 82.37 | 73.68 | 80 | 70 | 77.52 | 68.49 |
| 裸土地 | 85 | 79 | 88.52 | 80.94 | 81 | 81 | 82.37 | 73.68 | 72 | 71 | 77.52 | 68.49 |
| 机场 | 83 | 80 | 88.52 | 80.94 | 79 | 77 | 82.37 | 73.68 | 70 | 74 | 77.52 | 68.49 |
| 道路 | 82 | 77 | 88.52 | 80.94 | 77 | 74 | 82.37 | 73.68 | 74 | 69 | 77.52 | 68.49 |
2)基于特征级的精度评价
通过特征的属性差异,计算目标函数的适应度、类内距、类间距、运行时间、算法收敛时的迭代次数进行精度评价。其适应度函数即式(10),类内距和类间距函数为式(11)、(12)所示。
类内距函数:聚类内部的距离,即一个聚类中所有特征向量到聚类中心的距离。
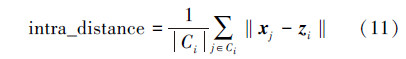
类间距函数:聚类之间的距离,即聚类的中心向量之间的距离。

评价结果的平均值如表 3所示,本文算法中,适应度值越小,说明分类精度越好,聚类之间的距离越大越好,保证了不同聚类之间的相似性较小。聚类内部的距离(8)越小越好,保证了聚类内部的样本与中心的偏离较小,聚类内部相似性较大。
| 分类算法 | 适应度 | 类内距 | 类间距 | 迭代次数 | 运行时间/min |
| DMQPSO | 5.842 9×105 | 2 753 | 4 267 | 292 | 81 |
| QPSO | 8.464 9×105 | 3 805 | 2 546 | 205 | 61 |
| K-Means | 2.992 3×106 | 4 157 | 1 563 | 53 | 0.4 |
从表 3可以看出,DMQPSO算法的适应度、类内距和类间距都优于其他2种算法,所以DMQPSO算法的分类精度最高。但是,其收敛速度和运行时间相对较慢,所以此算法有待改进。
5 结束语本文将QPSO算法进行改进,在QPSO算法中加入多样性变异机制,提出了一种新的遥感图像分类算法,由实验结果可以看出,在分类过程中,采用DMQPSO算法得到的图像的分类精度更高,并且QPSO算法相比K-Means 算法能找到更优的聚类中心,为研究人员进一步研究遥感图像分类提供了理论和实际参考价值。 但是其缺点是分类时间较长,需要对算法进一步改进。
| [1] | 蒋卫国, 陈强, 郭骥, 等. 基于HPSO和FCM的多光谱遥感图像湿地分类[J]. 光谱学与光谱分析, 2010, 30(12):3329-3333. JIANG Weiguo, CHEN Qiang, GUO Ji, et al. Classification of wetlands in multispectral remote sensing image based on HPSO and FCM[J]. Spectroscopy and Spectral Analysis, 2010, 30(12):3329-3333. |
| [2] | SHANKAR B U, MEHER S K, GHOSH A. Wavelet-fuzzy hybridization:feature-extraction and land-cover classification of remote sensing images[J]. Applied Soft Computing, 2011, 11(3):2999-3011. |
| [3] | 董杰, 沈国杰. 一种基于模糊关联分类的遥感图像分类方法[J]. 计算机研究与发展, 2012, 49(7):1500-1506. DONG Jie, SHEN Guojie. Remote sensing image classification based on fuzzy associative classification[J]. Journal of Computer Research and Development, 2012, 49(7):1500-1506. |
| [4] | 袁永福. 基于粒子群和互信息的高光谱图像波段选择和分类[D]. 西安:西安电子科技大学, 2014:61-73. YUAN Yongfu. Band selection and classification for hyperspectral image based on particle swarm optimization and mutual information[D]. Xi'an:Xidian University, 2014:61-73. |
| [5] | UIA D, MUNOZ-MARI J, CAMPS-VALLS G. Remote sensing image segmentation by active queries[J]. Pattern Recognition, 2012, 45(6):2180-2192. |
| [6] | AGRAWAL R K, BAWANE N G. Multiobjective PSO based adaption of neural network topology for pixel classification in satellite imagery[J]. Applied Soft Computing, 2015, 28:217-225. |
| [7] | SUN Jun, FENG Bin, XU Wenbo. Particle swarm optimization with particles having quantum behavior[C]//Congress on Evolutionary Computation. Portland:IEEE, 2004:325-331. |
| [8] | COELHO L S. Novel gaussian quantum-behaved particle swarm optimiser applied to electromagnetic design[J]. IET Science, Measurement & Technology, 2007, 1(5):290-294. |
| [9] | SUN Jun, CHEN Wei, FANG Wei, et al. Gene expression data analysis with the clustering method based on an improved quantum-behaved Particle Swarm Optimization[J]. Engineering Applications of ArtificialIntelligence, 2012, 25(2):376-391. |
| [10] | SUN Jun, WU Xiaojun, PALADE V, et al. Convergence analysis and improvements of quantum-behaved particle swarm optimization[J]. Information Sciences, 2012, 193:81-103. |
| [11] | URSEM R K. Diversity-guided Evolutionary Algorithm[M]// GUERVÓS J J M, ADAMIDIS P, BEYER H G, et al. Parallel Problem Solving from Nature-PPSN VII.Berlin Heidelberg:Springer, 2002, 2439:462-471. |
| [12] | RIGET J, VESTERSTROEM J S. A Diversity-guided particle swarm optimizer-the ARPSO[R]. Aarhus:Department of Computer Science, University of Aarhus, 2002. |



