2. 石家庄经济学院信息工程学院, 河北石家庄 050031
2. College of Information and Engineering, Shijiazhuang University of Economics, Shijiazhuang 050031, China
形式概念分析[1]是由德国的数学家R.Wille教授在1982年首次提出来的,作为一种进行数据分析和知识发现的有效的数学工具,用于概念的发现、排序和显示,所有概念连同它们之间的泛化和特化关系构成了概念格,也称为Galois格。从数据集中生成概念格的过程实际上是一种概念聚类的过程[2]。作为形式概念分析理论中的一种核心的数据结构,概念格逐渐成为数据分析和规则提取的一种有效工具。不确定性知识表示及推理是人工智能领域中的一个重要的课题。近年来,不确定性推理已发展为知识发现的一个新的分支,它包括定性推理和定量推理。定量不确定性推理方法通过对命题的数值计算提供了因果关系的数值趋势。它首先需要表示和测量不确定信息。不同的信息表示方法和不同的测量方法决定了不同的不确定性推理[7, 8, 9, 10]。所有方法的共同点是使用一个度量来衡量假设。在本文中,通过定义比形式概念更广泛的命题,基于一些基本概念如必然命题和充分命题,以及命题的确定度,讨论了命题的一些相关性质以及获得新命题的一些可行方法。探讨了基于决策形式背景中的命题推理方法。
1 基本概念以下给出有关形式概念分析的一些基本概念和性质,有关细节的描述在文献[1, 2, 3]。
定义1 设 (P,≤) 和 (Q, ) 是2个偏序集,若存在映射f:P→Q 与 g:Q→P,对于∀p1,p2∈P 和 ∀q1,q2∈Q,满足以下3个条件:
) 是2个偏序集,若存在映射f:P→Q 与 g:Q→P,对于∀p1,p2∈P 和 ∀q1,q2∈Q,满足以下3个条件:
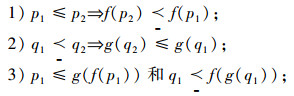
 )之间的Galois连接。
)之间的Galois连接。
在文献[2]中,给出了(f,g)是(P,≤)和(Q, )之间的Galois连接的充要条件为对于任意p∈P,q∈Q,有
)之间的Galois连接的充要条件为对于任意p∈P,q∈Q,有 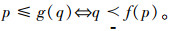 。
。
定义2 设 U 为非空有限对象集合,A 为非空有限属性集合,I 为 U 到A 之间的一个二元关系,即 I⊆U×A,则称三元组K=(U,A,I) 为一个形式背景。∀x∈U,a∈A,x 具有属性 a 表示为 (x,a)∈I,x 不具有属性 a 表示为(x,a)∉I。
设 K=(U,A,I) 为一个形式背景,对于B⊆A,X⊆U,可定义一组对偶算子如下:
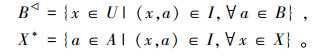
易证 (*, ) 形成偏序集(P(U),⊆)和(P(A),⊆) 之间的 Galois 连接。B
) 形成偏序集(P(U),⊆)和(P(A),⊆) 之间的 Galois 连接。B 表示具有B中全部属性的对象的集合,X* 表示X中全部对象具有的共同属性的集合。
表示具有B中全部属性的对象的集合,X* 表示X中全部对象具有的共同属性的集合。
∀x∈U,记x*为x*,∀a∈A,记a 为a
为a 。若∀x∈U,x*≠∅且x*≠A;∀a∈A,a
。若∀x∈U,x*≠∅且x*≠A;∀a∈A,a ≠∅且a
≠∅且a ≠U,则形势背景为正则的。若无特别说明,所提到的形势背景都是正则的。
≠U,则形势背景为正则的。若无特别说明,所提到的形势背景都是正则的。
定义3 若X*=B且B =X,就称(X,B)为形式背景K的一个概念[6]。其中X称为概念的外延,B称为概念的内涵。
=X,就称(X,B)为形式背景K的一个概念[6]。其中X称为概念的外延,B称为概念的内涵。
用 L(U,A,I) 表示形式背景 K=(U,A,I) 的全体概念,记 (X1,B1)≤(X2,B2) 当且仅当X1⊆X2(B1⊇B2),则“≤”是 L(U,A,I) 上的偏序关系。
性质 1[1] 假设K=(U,A,I)是一个形式背景,如果X,X1,X2⊆U,并且B,B1,B2⊆A,则

 1∪B
1∪B 2。
在形式背景(U,A,I)下,∀B⊆A,记IB=I∩(U×B),那么(U,B,IB)也是一个形式背景,对于运算X*(X⊆U),在(U,A,I)下用X*A表示,在(U,B,IB)下用X*B表示。显然,IA=I,X*A=X*,X*B=X*A∩B=X*∩B,X*B⊆X*。
2。
在形式背景(U,A,I)下,∀B⊆A,记IB=I∩(U×B),那么(U,B,IB)也是一个形式背景,对于运算X*(X⊆U),在(U,A,I)下用X*A表示,在(U,B,IB)下用X*B表示。显然,IA=I,X*A=X*,X*B=X*A∩B=X*∩B,X*B⊆X*。
定义4 称五元组 K=(U,A,D,I,J) 为一个决策形式背景,其中 (U,A,I) 和 (U,D,J) 为形式背景,U 为非空有限对象集,A 为非空有限条件属性集,D为非空有限决策属性集,且A∩D≠∅。
2 命题及性质本节主要给出通过属性关系定义的各种命题及其性质。
定义5 设K=(U,A,D,I,J)为一个决策形式背景,B⊆A,C⊆D,X⊆U,若B⊆X*A,则称 B 为 X 的必要条件属性,若X*A⊆B,则称B为X的充分条件属性;若C⊆X*D,则称C为X的必要决策属性,若X*D⊆C,则称C为X的的充分决策属性。
定理 1 设K=(U,A,D,I,J)为一个决策形式背景,X⊆U,B1,B2⊆A,C1,C2⊆D,则有性质:
1) X*A是X的必要条件属性,X*D是X的必要决策属性;
2) B为B A的必要条件属性,C为C
A的必要条件属性,C为C D的必要决策属性;
D的必要决策属性;
3) B1∪B2为B A1∩B
A1∩B A2的必要条件属性,C1∪C2为C
A2的必要条件属性,C1∪C2为C D1∩C
D1∩C D2的必要决策属性;
D2的必要决策属性;
4) B1∩B2为B A1∪B
A1∪B A2的必要条件属性,C1∩C2为C
A2的必要条件属性,C1∩C2为C D1∪C
D1∪C D2的必要决策属性。
D2的必要决策属性。
证明 由性质1中2) 易证定理1中1)、2)成立,由性质1中2) 和性质1中5)易证定理1中3)成立,由性质1中2) 和性质1中6)易证定理1中4)成立。
定义6 设K=(U,A,D,I,J)为一个决策形式背景,X⊆U,B⊆A,C⊆D,称(X,B)为条件命题,(X,C)为决策命题。若B⊆X*A,则称(X,B)为必然条件命题,表示“X具有条件属性B”,否则称为不确定条件命题;若C⊆X*D,则称(X,C)为必然决策命题,表示“X具有决策属性C”否则称为不确定决策命题。
定义7 设K=(U,A,D,I,J)为一个决策形式背景,X⊆U,B⊆A,C⊆D,若B⊆X*A,且C⊆X*D,则称 (X,B)→(X,C) 为必然蕴含命题,简记为(X,〈B,C〉)。
为了统一,将所有特殊命题统称为命题。
定义8 设(X1,B1)和(X2,B2)为两命题,若X1⊆X2且B1⊆B2,则称(X1,B1)为(X2,B2)的子命题,(X2,B2)为(X1,B1)的拓命题。
定理 2 设(X,B)为一个命题,则有
1)(X,B) 是 (X* ,B) 的子命题;
,B) 的子命题;
2)(X,B *) 是 (X,B) 的拓命题;
*) 是 (X,B) 的拓命题;
3)(X∪B ,B) 是 (X,B) 的拓命题;
,B) 是 (X,B) 的拓命题;
4)(X,B∪X*) 是 (X,B) 的拓命题;
5)(X* ,B∩X*) 不是 (X,B) 的子命题,也不是 (X,B) 拓命题。
,B∩X*) 不是 (X,B) 的子命题,也不是 (X,B) 拓命题。
证明 由性质1和定义8易证。
3 命题的确定度定义 9 设 (X,B) 为一个命题,称
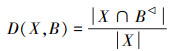
定理 3 命题(X,B)的确定度具有以下性质:
1)0≤D(X,B)≤1;
2)(X,B)为必然命题当且仅当有D(X,B)=1;
3)若B ⊆X1⊆X2,则D(X2,B)≤D(X1,B)。
⊆X1⊆X2,则D(X2,B)≤D(X1,B)。
证明 由定义9 易证(1),(3)。下证(2)成立。
若(X,B)为必然命题,则有B⊆X*,由性质1可知X* ⊆B
⊆B ,又X⊆X*
,又X⊆X* ,故有X⊆B
,故有X⊆B ,
则X∩B
,
则X∩B =X,由定义9有D(X,B)=1。
=X,由定义9有D(X,B)=1。
若D(X,B)=1,则X∩B =X,所以X⊆B
=X,所以X⊆B ,由性质1可知B
,由性质1可知B *⊆X*,又B⊆B
*⊆X*,又B⊆B *,所以有B⊆X*,由定义6可知(X,B)为必然命题。
*,所以有B⊆X*,由定义6可知(X,B)为必然命题。
定理 4 设(X,B)为一个命题,则有
1)D(X* ,B)≤D(X,B),若(X*
,B)≤D(X,B),若(X* ,B)为必然命题,则(X,B)也为必然命题;
,B)为必然命题,则(X,B)也为必然命题;
2)D(X,B *)=D(X,B),若(X,B)为必然命题,则(X,B
*)=D(X,B),若(X,B)为必然命题,则(X,B *)也为必然命题。
*)也为必然命题。
证明 1)由X⊆X* 与命题确定度定义,有
与命题确定度定义,有
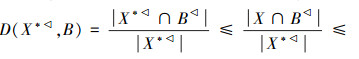
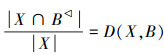 若(X*
若(X* ,B) 为必然命题,则B⊆X*
,B) 为必然命题,则B⊆X* *,又X*=X*
*,又X*=X* *,所以B⊆X*,即(X,B)为必然命题。
*,所以B⊆X*,即(X,B)为必然命题。
2)由性质B =B
=B *
* 与命题确定度定义,有
与命题确定度定义,有 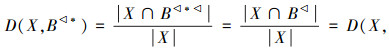 B)。若(X,B) 为必然命题,则有B⊆X*,故有X*
B)。若(X,B) 为必然命题,则有B⊆X*,故有X* ⊆B
⊆B ,有 B
,有 B *⊆X*
*⊆X* *=X*,即 (X,B
*=X*,即 (X,B *) 也为必然命题。
*) 也为必然命题。
定理 5 设(X,B)为一个不确定命题,则有
1)D(X∪B ,B)≥D(X,B);
,B)≥D(X,B);
2)D(X,B∪X*)≥ωD(X,B);
3)D(X∪B ,B∪X*)≥ωD(X,B)。
,B∪X*)≥ωD(X,B)。
其中 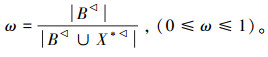
证明 
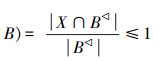 故D(X∪B
故D(X∪B ,B)≥D(X,B)。
,B)≥D(X,B)。
2)由性质 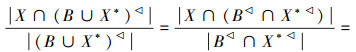
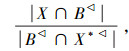 而
而 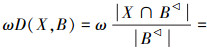
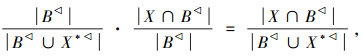 ,又
,又  ,故有 D(X,B∪X*)≥ωD(X,B)。
,故有 D(X,B∪X*)≥ωD(X,B)。
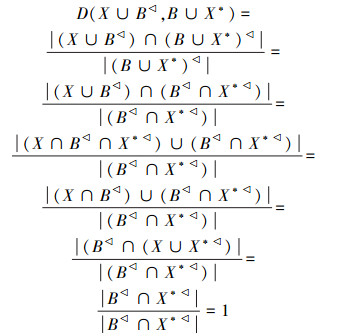
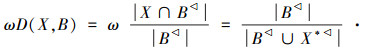
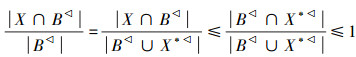 ,所以有 D(X∪B
,所以有 D(X∪B ,B∪X*)≥ωD(X,B)。
,B∪X*)≥ωD(X,B)。
定理 6 D((X1∪X2)*,B)=D(X1*,B)+D(X2*,B)-D(X1*∪X2*,B)。
证明 D((X1∪X2)*,B)=
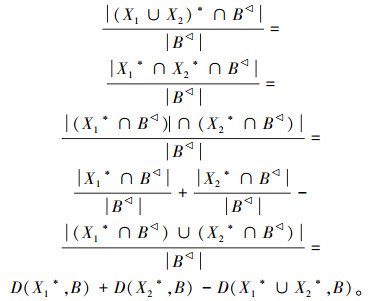
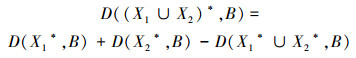
定理 7 D((X1∩X2)*,B)≥D(X1*,B)+D(X2*,B)-D(X1*∩X2*,B)。
证明
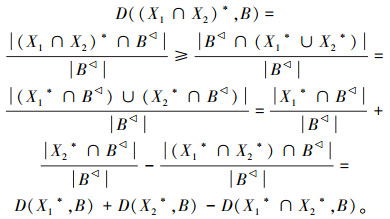
定理 8 设K=(U,A,D,I,J)为一个决策形式背景,X⊆U,B⊆A,C⊆D,若(X,B)为必然命题,且D(B ,C)≤ε,则D(X,C)≤ε。
(此处0≤ε≤1)。
,C)≤ε,则D(X,C)≤ε。
(此处0≤ε≤1)。
证明 若(X,B)为必然命题,则由定义6有B⊆X*,所以有 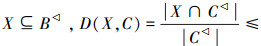
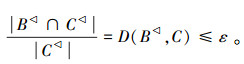 。
。
4 结束语
本文通过弱化形式概念构成的条件,定义了比概念更广泛的命题,基于一些基本概念如必然命题和充分命题,确定了一个命题的程度即确定度,并讨论了命题的一些相关性质以及获得一些新命题的有效方法。 探讨了基于决策形式背景中的命题推理方法,为命题之间的不确定推理提供了一种新的框架。 在后续的研究中,会讨论更广泛的、 更复杂的如不完备的形式背景及模糊形式背景的命题推理。本文的讨论还是一个尝试,相关研究还有待进一步深入。
| [1] | GANTER B, WILLE R. Formal concept analysis:mathematical foundations[M]. Berlin:Springer, 1999. |
| [2] | WILLE R. Restruturing lattice theory:an approh based on hierarhies of conepts[M]//RIVAL I. Ordered Sets. Netherlands:Springer, 1982:445-470. |
| [3] | BELOHLAVEK R. Fuzzy Galois connections[J]. Mathematical Logic Quarlerly, 1999, 45(4):497-504. |
| [4] | WEI Ling, QI Jianjun, ZHANG Wenxiu. Attribute reduction theory of concept lattice based on decision formal contexts[J]. Science in China Series F:Information Sciences, 2008, 51(7):910-923. |
| [5] | WANG Hong, ZHANG Wenxiu. Approaches to knowledge reduction in generalized consistent decision formal context[J]. Mathematical and Computer Modelling, 2008, 48(11/12):1677-1684. |
| [6] | LI Jinhai, MEI Changlin, LYU Yuejin. Knowledge reduction in decision formal contexts[J]. Knowledge-Based Systems, 2011, 24(5):709-715. |
| [7] | CHEN Shuwei, XU Yang, MA Jun. A linguistic truth-valued uncertainty reasoning model based on lattice-valued logic[M]//WANG Lipo, JIN Yaochu. Fuzzy Systems and Knowledge Discovery. Berlin Heidelberg:Springer-Verlag, 2005, 3613:276-284. |
| [8] | BELLAMN R E, ZADEH L A. Decision-making in a fuzzy enviroment[J]. Management Science, 1970, 17(4):B-141-B-164. |
| [9] | BOBILLO F, STRACCIA U. Generalized fuzzy rough description logics[J]. Information Sciences, 2012, 189:43-62. |
| [10] | KANEIWA K, KAMIDE N. Paraconsistent computation tree logic[J]. New Generation Computing, 2011, 29(4):391-408. |



