传统的二值逻辑中,命题的真值只有2种可能,是与非,而事实上对事物的描述从来没有如此确定。对于同一命题,不同的人有不同的看法,不同的环境中有不同的特性,没有绝对的对与错、是与非。1965年,L.A.Zadeh提出了模糊数学的理论与方法,为解决这个问题提供了一个工具,进而模糊逻辑[1]将模糊命题映射到闭区间[0, 1]上,扩充了命题真值的范围,更客观地反映了事物特征。基于模糊逻辑的模糊推理方法目前已在众多领域取得了显著的成效[2, 3, 4]。1983 年,考虑模糊隶属函数的对立方面——非隶属度,K.T.Atanassov 提出了直觉模糊集的概念[5]。直觉模糊集及其推理方法已成为目前研究的热点之一[6, 7, 8]。1996年,史开泉教授提出双枝模糊集理论[9, 10],将隶属函数扩展为模糊接吻函数S(x)∈[-1,1],进一步扩大了模糊集的研究领域。通过分解定理说明了双枝模糊集与普通集的转化关系。刘刚等[11, 12]在双枝模糊集基础上,建立了双枝模糊逻辑的框架,对单枝模糊逻辑进行了合理的扩充。作者认为,在很多情况下,不易判断命题是否为真或假,事物本身带有极大的不确定性。命题的真度、伪度和不确定度三者同时存在,并形成一个相互作用、相互转化的系统。为了更为客观、全面、系统地刻画事物,作者以集对分析理论[13, 14]中的联系数为基本工具,提出了集对逻辑的定义,并证明了其主要运算律[15]。本文以集对逻辑的基本方法为主要工具,提出一种新的近似推理模式与方法。
1 集对逻辑 1.1 基本概念对于一个命题A,如果得到其为真、假、不确定的程度分别为a、b、c,则可将A的真值表示为联系数的形式,记作:μ=a+bi+cj。具有该种形式真值的命题成为集对命题。
定义1 设集对命题的集合S,若映射μ:S→{μμ=a+bi+cj}满足:

则称映射μ为S上的真值函数,μ(A)称为集对命题A的真值。当给定集对命题A以具体的真值时,称为给集对命题A赋值。
定义2 对于集对公式A和B,当且仅当对A、B中所含集对命题的一切赋值都有μ(A)≡μ(B)时,称A、B为等值公式,并记作A=B。
定义3 如果集对命题A的真值为μ(A)=1,则称A为S-真命题。
定义4 如果集对命题A的真值为μ(A)=i,则称A为S-不确定命题。
定义5 如果集对命题A的真值为μ(A)=j,则称A为S-假命题。
定义6 对于集对命题A,如果其真度为a(A),伪度为c(A)j,则其不确定度为b(A)=1-a(A)-c(A),且命题A的真值为
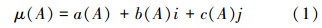
设A,B∈S,μ(A)=a(A)+b(A)i+c(A)j和μ(B)=a(B)+b(B)i+c(B)j,针对集对真值的真度和伪度分别进行双枝模糊逻辑的演算规则,则:析取式、合取式和否定式的真值如下:
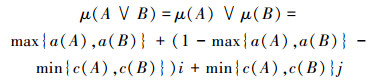

约定:A,B,C∈S
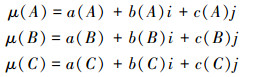
定律1 幂等律
μ(A∧A)=μ(A),μ(A∨A)=μ(A)
定律2 交换律
μ(A∧B)=μ(B∧A),μ(A∨B)=μ(B∨A)
定律3 吸收律
μ(A∨(A∧B))=μ(A),μ(A∧(A∨B))=μ(A)
定律4 结合律
μ((A∧B)∧C)=μ(A∧(B∧C))
μ((A∨B)∨C)=μ(A∨(B∨C))
定律5 分配律
μ(A∨(B∧C))=μ((A∨B)∧(A∨C))
μ(A∧(B∨C))=μ((A∧B)∨(A∧C))
定律6 在分配格(S,∨,∧)中有最大元1和最小元j,且满足
μ(A)∨j=μ(A),μ(A)∧j=j
μ(A)∨1=1,μ(A)∧1=μ(A)
定律7 对合律,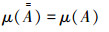
定律8 摩根律

形如“A:x是a”的陈述句称为判断句,x称为语言变元,是论域X中的任一特定对象。若A所表示的概念是集对的,即其真值可用联系数来表示,则称判断句A为集对判断句,其真值记为
μ(A)=a(A)+b(A)i+c(A)j
定义7 对于判断句“A:x是a”和“B:x是b”,称“若A,则B”为推理句,记作A→B。若A、B均为集对判断句,则称为集对推理。
定义8 集对判断句的蕴含关系为
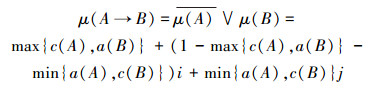
集对判断句分别从肯定、否定、不确定3个方面描述了命题的特征,是一种更为客观的推理形式,是对模糊推理及双枝模糊推理的补充与完善。
2.2 单论域集对推理设μ(A)=a(A)+b(A)i+c(A)j, μ(B)=a(B)+b(B)i+c(B)j 则对于以上给出的集对蕴含式,有:
定义9 如果A→B的真值为μ(A→B)=1,则称A→B对x集对真,简记为S-真。
定义10 如果A→B的真值为μ(A→B)=i,则称A→B对x集对不确定,简记为S-不确定。
定义11 如果A→B的真值为μ(A→B)=j,则称A→B对x集对假,简记为S-假。
定律9 若对于集对命题A,B,其真值分别为
μ(A)=a(A)+b(A)i+c(A)j
μ(B)=a(B)+b(B)i+c(B)j
则有以下性质成立:1)若A对x为S-真命题,则A→B与B等值;
2)若A对x为S-假命题,则A→B对x必为S-真;
3)若B对x为S-真命题,则A→B对x必为S-真;
4)若B对x为S-假命题,则A→B与A互逆。
证明 根据定义知,
1)若A对x为S-真命题,即μ(A)=1,则
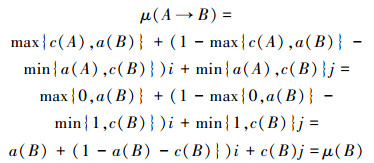
2)若A对x为S-假命题,即μ(A)=j,则
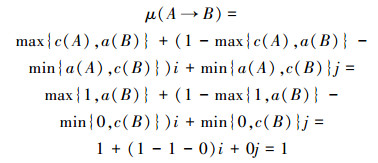
3)若B对x为S-真命题,即μ(B)=1,则


4)若B对x为S-假命题,即μ(B)=j,则
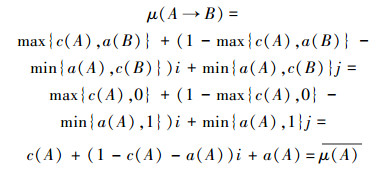
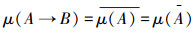 因此A→B与A互逆。
因此A→B与A互逆。
定律10 若μ(A)=a(A)+b(A)i+c(A)j,μ(B)=a(B)+b(B)i+c(B)j,且A对x为S-不确定命题,则有:
1)若B对x为S-真命题,则A→B为S-真;
2)若B对x为S-假命题,则A→B为S-不确定。
3)若B对x为S-不确定命题,则A→B为S-不确定。
证明:由题意μ(A)=i,根据定义知,
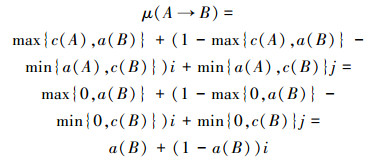
当a(B)=0,μ(A→B)=i,A→B为S-不确定。得证。
定律11 复合蕴含规则。设A,B,C∈S,且
μ(A)=a(A)+b(A)i+c(A)j
μ(B)=a(B)+b(B)i+c(B)j
μ(C)=a(C)+b(C)i+c(C)j
若A→B对x为S-真,B→C对x为S-真,则A→C对x为S-真。
证明 由蕴含式A→B对x为S-真,知:  ,则
,则 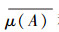 和μ(B)必定至少有一个为1。若μ(B)=1,则由定律9知μ(C)=1,于是得到μ(A→C)=1,即A→C对x为S-真。若
和μ(B)必定至少有一个为1。若μ(B)=1,则由定律9知μ(C)=1,于是得到μ(A→C)=1,即A→C对x为S-真。若 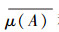 =1,又有B→C对x为S-真,则必有μ(C)=1,即得A→C对x为S-真。证毕。
=1,又有B→C对x为S-真,则必有μ(C)=1,即得A→C对x为S-真。证毕。
对于集对蕴含式推理的一般情况,见表 1。
| 序号 | 划分 | 等级 | 集对势 | a,b,c大小关系 | 集对推理 |
| 1 | 均势 | 一级 | 微均势 | a=c,b>a | S-微均 |
| 2 | 均势 | 二级 | 弱均势 | a=c,b=a | S-弱均 |
| 3 | 均势 | 三级 | 强均势 | a=c,a>b>0 | S-强均 |
| 4 | 均势 | 四级 | 准均势 | a=c,b=0 | S-准均 |
| 5 | 同势 | 一级 | 准同势 | a>c,b=0 | S-准同 |
| 6 | 同势 | 二级 | 强同势 | a>c,c>b | S-强同 |
| 7 | 同势 | 三级 | 弱同势 | a>c,a>b>c | S-弱同 |
| 8 | 同势 | 四级 | 微同势 | a>c,b>a | S-微同 |
| 9 | 反势 | 一级 | 准反势 | a | S-准反 |
| 10 | 反势 | 二级 | 强反势 | a | S-强反 |
| 11 | 反势 | 三级 | 弱反势 | a | S-弱反 |
| 12 | 反势 | 四级 | 微反势 | a | S-微反 |
| 13 | 不确定同一势 | c=0,a>b | S-不确定同 | ||
| 14 | 不确定不确定势 | c=0,a≤b | S-不确定不确定 | ||
| 注:序号1~12是在a≠0,c≠0条件下形成的集对势;当c=0,b≠0,a≠0时为集对的不确定势。集对推理与集对势形成了一一对应关系。 | |||||
基于集对命题逻辑的推理将传统推理的结果细分为更多可能的结果,更加客观地反映了事物的不确定性。
2.3 双论域集对推理上节给出的推理规则是在同一个论域中展开的,而在现实生活中往往会见到形如“x是a,则y是b”的集对推理句,涉及2个变元x和y,它们分别属于X与Y这2个不同论域。若描述为“Ax:x是a,By:y是b”,则可记作Ax→By。此时,以上推理规则便不再适用。为了解决这个问题,这里给出集对关系和联系域的概念。
定义12 给定2个不同的论域X与Y,对于任意x∈X,y∈Y,在X∪Y的某个问题背景下得到它们的联系度为μ(x,y)=a+bi+cj,若a+b≥0.5,则称x和y具有集对关系;如果对于∀x∈X,∀y∈Y都具有集对关系,则称X与Y具有集对关系。
集对关系具有自反性和对称性。
定义13 由X×Y中所有具有集对关系的元素(x,y)组成的论域称为X与Y的联系域,记作 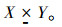 。
。
双论域集对推理在联系域 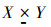 中展开。
中展开。
定义14 在 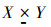 中,若Ax和By的真值为
中,若Ax和By的真值为

则双论域集对蕴含句Ax→By的真值定义为
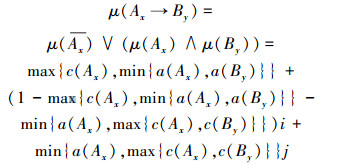
定义15 如果集对蕴含式Ax→By的真值为μ(Ax→By)=1,则称Ax→By为集对真,简记为S-真。
定义16 如果集对蕴含式Ax→By的真值为μ(Ax→By)=i,则称Ax→By为集对不确定,简记为S-不确定。
定义17 如果集对蕴含式Ax→By的真值为μ(Ax→By)=j,则称Ax→By为集对假,简记为S-假。
定律12 若μ(Ax)=a(Ax)+b(Ax)i+c(Ax)j和μ(Ay)=a(By)+b(By)i+c(By)j,则以下性质成立:
1)若Ax对x为S-真命题,则集对蕴含式Ax→By与By等值;
2)若Ax对x为S-假命题,则集对蕴含式Ax→By必为S-真;
3)若Ax对x为S-不确定命题,则集对蕴含式Ax→By必为S-不确定;
4)若By对x为S-真命题,则集对蕴含式Ax→By与Ax等值或互逆;
5)若By对x为S-假命题,则集对蕴含式Ax→By与Ax互逆。
证明 根据定义
1)若Ax对x为S-真命题,即μ(Ax)=1,则

即μ(Ax→By)=μ(By),因此集对蕴含式Ax→By与By等值。
2)若Ax对x为S-假命题,即μ(Ax)=j,则
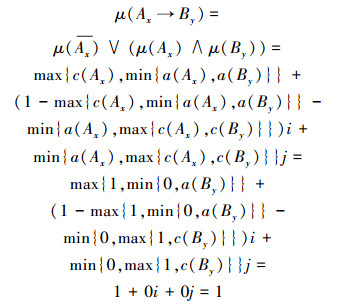
即μ(Ax→By)=1,因此集对蕴含式Ax→By为S-真。
3)若Ax对x为S-不确定命题,μ(Ax)=i,则

即μ(Ax→By)=i,因此集对蕴含式Ax→By必为S-不确定。
4)若By对x为S-真命题,即μ(By)=1,则
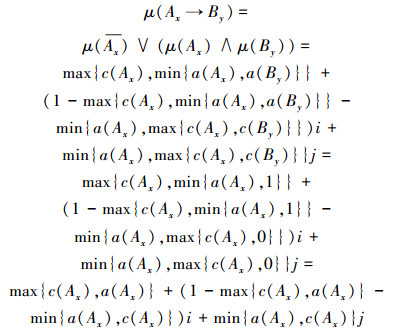

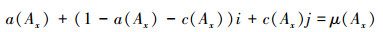

5)若By对x为S-假命题,即μ(By)=j,则
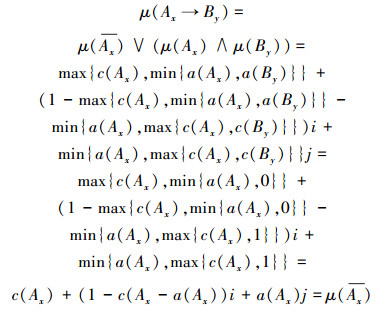
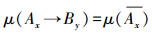 ,则集对蕴含式Ax→By与Ax互逆。
3 结束语
,则集对蕴含式Ax→By与Ax互逆。
3 结束语
本文基于集对逻辑的基本方法,给出了集对蕴含式的定义,以此建立了的单论域的集对推理形式;然后定义了一种集对关系,以及集对关系形成的论域——联系域,给出了联系域上的双论域集对推理形式。集对推理模式的建立对于集对分析理论的逐步完善及其在各领域中的应用提供了一个新的思路与工具,是对经典逻辑和模糊逻辑的一种补充和完善。集对逻辑及其推理方法针对不确定性问题展开研究,从肯定、犹豫和否定3个方面描述人们对事物的复杂认知。用三维联系数刻画命题的真值,更具一般性。集对逻辑及其推理方法的研究仍处于初步阶段,仍需要进一步研究。
| [1] | ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3):338-353. |
| [2] | 张胜礼. 带有矛盾否定、对立否定和中介否定的模糊推理[J]. 模式识别与人工智能, 2014, 27(7):599-610. ZHANG Shengli. Fuzzy reasoning with contradictory, opposite and medium negation[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(7):599-610. |
| [3] | 王国俊, 段景瑶. 适宜于展开模糊推理的两类模糊度量空间[J]. 中国科学:信息科学, 2014, 44(5):623-632. WANG Guojun, DUAN Jingyao. Two types of fuzzy metric spaces suitable for fuzzy reasoning[J]. Scientia Sinica:Informations, 2014, 44(5):623-632. |
| [4] | 申蔓蔓, 乐晓波, 周凯卿. 一种基于新的直觉模糊Petri网的模糊推理算法[J]. 计算机工程与科学, 2015, 37(2):354-358. SHEN Manman, LE Xiaobo, ZHOU Kaiqing. A novel fuzzy reasoning algorithm based on intuitionistic fuzzy petri nets[J]. Computer Engineering & Science, 2015, 37(2):354-358. |
| [5] | ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1):87-96 |
| [6] | 李弼程, 王瑾, 林琛. 基于直觉模糊推理的网络舆情预警方法[J]. 计算机应用研究, 2010, 27(9):3312-3315. LI Bicheng, WANG Jin, LIN Chen. Method of online public opinions pre-warning based on intuitionistic fuzzy reasoning[J]. Application Research of Computers, 2010, 27(9):3312-3315. |
| [7] | 李晓冰, 徐扬. 基于直觉模糊推理的多属性群决策方法研究[J]. 计算机应用研究, 2012, 29(2):533-535, 541. LI Xiaobing, XU Yang. Method of multiple attribute group decision making based on intutionistic reasoning[J]. Application Research of Computers, 2012, 29(2):533-535, 541. |
| [8] | 雷阳, 雷英杰, 冯有前, 等. 基于直觉模糊推理的目标识别方法[J]. 控制与决策, 2011, 26(8):1163-1168. LEI Yang, LEI Yingjie, FENG Youqian, et al. Techniques for target recognition based on intuitionistic fuzzy reasoning[J]. Control and Decision, 2011, 26(8):1163-1168. |
| [9] | 史开泉. 双枝模糊集(I)[J]. 山东工业大学学报, 1998, 28(2):127-134. SHI Kaiquan. Both-branch fuzzy sets(I)[J]. Journal of Shandong University of Technology, 1998, 28(2):127-134. |
| [10] | 刘纪芹, 史开泉. 双枝模糊集模糊性度量[J]. 系统工程与电子技术, 2007, 29(5):732-736. LIU Jiqin, SHI Kaiquan. Measures of fuzziness in both-branch fuzzy sets[J]. Systems Engineering and Electronics, 2007, 29(5):732-736. |
| [11] | 刘刚, 徐衍亮, 赵建辉, 等. 双枝模糊逻辑[J]. 计算机工程与应用, 2003, 39(30):96-98. LIU Gang, XU Yanliang, Zhao Jianhui, et al. Both-branch fuzzy logic[J]. Computer Engineering and Applications, 2003, 39(30):96-98. |
| [12] | 刘刚, 刘强. 双枝模糊推理框架[J]. 计算机工程与应用, 2004, 40(32):102-105. LIU Gang, LIU Liang. Frame of both-branch fuzzy inference[J]. Computer Engineering and Applications, 2004, 40(32):102-105. |
| [13] | 赵克勤. 集对分析及其初步应用[M]. 杭州:浙江科学技术出版社, 2000:9-41. |
| [14] | 赵玉铃, 张廉. 集对分析联系数在黑启动vague集决策中的应用研究[J]. 智能系统学报, 2014, 9(5):632-640. ZHAO Yuling, ZHANG Lian. Application of the set-pair analysis connection number in decision-making of black-start vague set[J]. CAAI Transactions on Intelligent Systems, 2014, 9(5):632-640. |
| [15] | 杨亚锋. 集对逻辑及其运算定律[J]. 辽宁工程技术大学学报:自然科学版, 2013, 32(2):249-252. YANG Yafeng. Set pair logic and its operation theorems[J]. Journal of Liaoning Technical University:Natural Science, 2013, 32(2):249-252. |



