聚类分析是一种广泛使用的数据分析方法,一直被应用于多个领域,特别是在数据挖掘、模式识别、图像处理等领域应用十分广泛。K-means[1]是最经典且使用最为广泛的聚类算法,其过程简单快捷,容易实现。为了克服K-means对初始聚类中心敏感的缺陷,Zhang等[2]于1999年提出一种K-调和均值(K-harmonic means,KHM)算法,具有较高的稳定性、收敛速度快,但由于其与K-means同样基于划分的原理,仍存在易陷于局部最优的问题。
目前,对于KHM算法的研究主要是结合智能优化算法进行改进,以充分利用其全局搜索能力,如融合粒子群[3]、变邻域搜索[4]、改进候选组搜索[5]等混合聚类算法。此外,将模糊概念引入KHM中也得到了一定的关注[6, 7]。目前,各种群智能优化算法已被广泛地应用于各个领域中[8, 9, 10, 11],并且依据没有免费的午餐定律,本文提出新的混合聚类算法。萤火虫算法(firefly algorithm,FA)是由剑桥学者Yang等[12, 13]在2008年提出的一种新颖的群智能算法,具有结构简单、可调参数少、宜于并行处理等特点,可以有效解决各种优化问题,并能够成功应用到聚类问题中提高算法的准确性和鲁棒性[14]。很多学者已经对它开展了不少研究工作,引入混沌原理改进的FA具有一定的优势,Fister等[15]对现有的混沌萤火虫算法(chaos-based firefly algorithm,CFA)进行了总结,它们的主要思想都是基于算法参数的改进,其中Gandomi等[16]采用各种混沌映射模型进行了比较全面的对比分析。然而,仅对参数的调整无法更全面有效地利用混沌优化的优点,混沌局部搜索(chaotic local search,CLS)[9, 10]是一种能够有效提高算法优化性能的策略。
本文从进一步提高FA的优化性能出发,提出一种新颖的CFA,并将其融入到KHM以获得一种更有效的混合聚类方法。在FA中引入一种并行混沌局部搜索策略,将CLS与并行混沌优化(parallel chaotic optimization,PCO)[17, 18]相结合,提高FA的局部搜索能力,具有更高的搜索效率,并能够有效避免局部最优。将这种改进的CFA融入到KHM中优化其目标函数,通过对实际数据集的实验可以看出本文所提的聚类算法能够获得更好的性能指标,有效抑制了陷入局部最优的问题。
1 算法概念与定义 1.1 K-调和均值算法K-调和均值算法的原理基本上与K-means是相似的,不同的是其使用调和均值(harmonic means,HM)代替算术均值来计算目标函数,能够有效解决对初始类中心点选取的敏感性问题。假定数据集X=[x1 x2 … xn]包含n个数据,它们被划分到k个聚类簇,每个簇的中心用cj(j=1,2,…,k)表示,KHM的目标函数为[3]
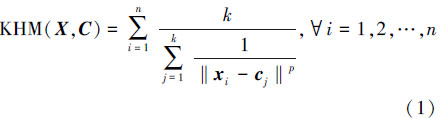
这里采用欧式距离计算样本到聚类中心的距离,参数p对算法的性能具有重要的影响,且当p≥2时聚类的效果比较好[2]。算法通过不断地迭代使目标函数值不断减小并保持稳定,每次迭代过程中,各个簇的中心点cj(j=1,2,…,k)的更新如下[3]。
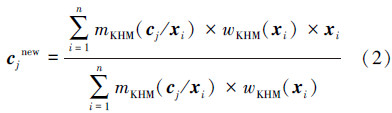
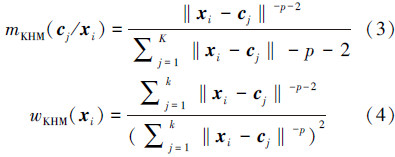
在FA中萤火虫彼此吸引主要取决于2个因素:亮度和吸引度。亮度决定了个体所处位置的好坏及其移动方向,吸引度决定了移动的距离,通过亮度和吸引度的不断更新,实现目标优化。通常直接利用目标函数值的大小表示萤火虫i的亮度Ii,即Ii=f(xi),xi=[xi1 xi2 … xid]。FA的相关定义如下[12, 13]:
定义1 萤火虫i与j之间的吸引度为

定义2 萤火虫i被更亮的萤火虫j吸引而移动的位置为
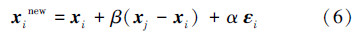
基本的FA缺乏变异机制,当处于局部极值时难以摆脱,且当前最优解xpg周围是搜索到更优解的最有利的区域,而FA在优化过程中采用对其随机扰动的方式,搜索效率不高。混沌优化方法能够有效地跳出局部最优并搜索到全局最优解,现有文献对混沌模型的研究非常广泛,如logistic映射、Sinusoidal映射、Gaussian映射等[16, 19]。文献[9, 10]中采取一种改进logistic映射分别与粒子群(particle swarm optimization,PSO)算法和差分进化算法融合提出2种有效的基于CLS的混合优化算法,成功用于短期梯级水电系统调度问题,并且在文献[19]中验证了这种混沌映射的优势,它具有较大的李雅普诺夫指数。logistic映射模型为[19]
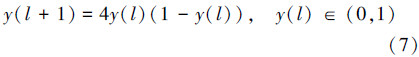
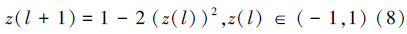
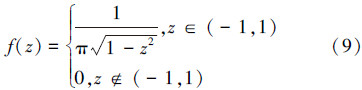
由式(9)可以看出改进logistic映射可以将混沌变量的搜索空间拓展到(-1,1),在接近边界-1和1处具有较大的概率密度值,因此具有更好的遍历性、随机性。因此,本文利用改进logistic映射在当前最优解附近直接搜索,其本质上属于一种混沌干扰法,即产生许多局部最优解的邻域点,以增强搜索到全局最优解的概率。与此同时,适应度值仅次于最优解xpg的次优解xps同样对搜索到更优解具有一定的价值,文献[20]中以最优点和次优点为基础进行反射、延伸、收缩等步骤的单纯形法也为本文提供一定的启发。为了更直观地分析,在图 1中分别给出二维的单峰和多峰搜索空间的2种特殊情况的次优解与最优解局部搜索区域,它们的局部搜索半径均相等,并且假定越往内适应度值越好。从图 1(a)、(b)中可见2种特殊情况下次优解相对于最优解均具有更好的搜索潜力。
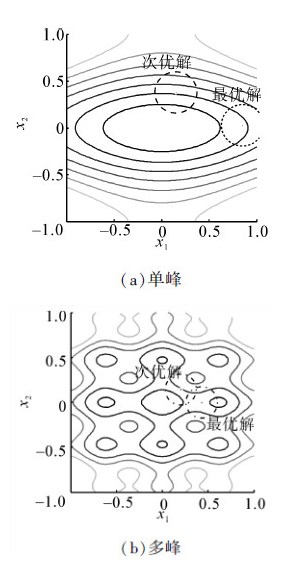 |
| 图 1 2种特殊情况的最优解与次优解局部搜索区域Fig. 1 Two particular types of local search region around the best and second best solutions |
为了进一步提高搜索效率,提出一种并行混沌局部搜索(parallel chaotic local search,PCLS)策略,采用并行混沌优化的思想产生N个混沌局部变量对次优解和最优解并行扰动,不但克服传统CLS的串行机制搜索精确解效率不高、收敛稳定性不强等缺点[9, 10],还能够有效地兼顾最优解与次优解。当最优解和次优解接近时可将它们的作用视为相等,不接近时则能够有效地拓展局部搜索空间。每次迭代后取N个并行变量与xpg和xps综合排序获得新的最优解和次优解,有效地提高算法搜索能力。
考虑到文献[17, 18]中PCO结合了粗搜索与细搜索的策略以平衡算法的探索与开发性能,为了使并行混沌局部搜索萤火虫算法(parallel chaotic local search firefly algorithm,PCLSFA)在前期进行一定的粗搜索,可在前Tmax1次迭代直接执行FA,PCLSFA的具体过程为:
1)初始化萤火虫个体的位置并计算其对应的目标函数值Ii作为亮度,初始化迭代次数t=0,最大迭代次数设为Tmax1,粗搜索迭代次数Tmax11。
2)执行FA不断更新亮度,最亮的个体即为当前最优解xpg,并且次优解为xps,若t>Tmax11,则采用PCLS在它们附近寻优作为细搜索。
3)设置当前混沌搜索次数l=0,在上文几个断点外的区域初始化混沌变量-1 < zij(0) < 1 (i=1,2,…,N; j=1,2,…,m),N为并行变量数,m为单变量维数,则zij表示第i个并行变量的第j维。此外,中间变量矩阵为Y,PCLS最大迭代次数为Cmax。
①考虑到大多数情况下xpg具有更好的搜索潜力,令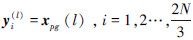 ,且
,且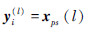 ,
,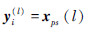 ,…,N,使用式(8)确定第l+1次迭代的混沌扰动变量zij(l+1)。
,…,N,使用式(8)确定第l+1次迭代的混沌扰动变量zij(l+1)。
②混沌变量与收缩因子βt成比例,通过混沌扰动产生N个新变量如式(10)所示。


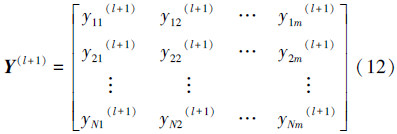
③计算每个新变量所对应的目标函数值为f(yi(l+1)),并将Y(l+1)与xpg(l+1)、xps(l+1)合并,对这N+2个变量的适应度值进行排序,得到第l+1次迭代中的最优解xpg(l+1)和次优解xps(l+1)。
④l=l+1,若l < Cmax,转向①;否则转向4)。
4)t=t+1,若t < Tmax,转向2),且随机选取一个萤火虫个体用3)中获得的xpg替换并更新其亮度;否则停止迭代,输出全局最优解。
2.2 提高种群多样性的策略由于FA缺乏保持种群多样性的操作,降低了算法探索到全局最优解的能力,因此需要采取一定的措施来解决这一问题。本文中算法每迭代Np次时,找出适应度值最差的nc%的个体并采用混沌重构法生成新的个体替代它们。对于各维尺度相等的优化问题,直接计算出当前种群所有维空间的最大值xmax和最小值xmin作为各维的统一边界。对于各维尺度不相等的优化问题,对边界向量不断地收缩,初始时第j维的边界等于定义域[aj,bj],当达到第Np次迭代的最优个体为x*,根据式(13)收缩边界。
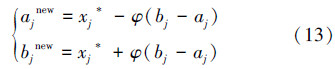
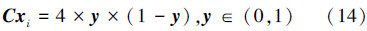
最后再将其转换到当前种群变量的取值空间如式(15)所示,获得替换种群并更新其适应度值。
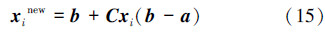
这里随着迭代次数的增加对边界范围不断收缩,在各个不同阶段生成不同尺度的混沌变量,能够避免直接根据初始的定义域随机生成替代个体时效率不高的问题,且同样能够改善种群多样性。
2.3 改进FA的收敛性分析及复杂度分析目前,FA还没有很完备的数学理论基础[12, 13],但已有的仿真实验结果表明FA具有较高的寻优精度和收敛速度,是一种有效的优化方法。本文改进算法与基本FA的不同之处为迭代Tmax11次后增加了PCLS过程,故只需证明3)过程的收敛性,即可证明PCLSFA的收敛性优于FA。从测度论上进行分析,由于PCLS属于下降算法,并且它具有很好的遍历性,因而设Rg表示全局最优点x*的可行域。总迭代次数为t时(t>Tmax11),在执行2)后的当前最优解xpg和次优解xps落入Rg的事件集合为A0,P(A0)≤1,PCLS每次迭代后产生的序列矩阵y(l)且与xpg(l)、xps(l) (l=1,2,…,Cmax)合并后落入Rg的事件集合为Al,因此A1⊂A2⊂…⊂ACmax,概率测度单调不减,故P(ACmax)≥…≥P(A2)≥P(A1)。可知执行3)之后具有更高的概率落入全局最优点x*的可行域,故PCLSFA的收敛性优于FA,接下来通过对基准函数的仿真实验能够进一步验证其收敛性。此外,当忽略对目标函数的计算时,FA的时间复杂度为O(Tmax1•Npop2),且PCLSFA的时间复杂度为O(Tmax•Npop2+Tmax2•Cmax•N),(Tmax2=Tmax1-Tmax1)。
2.4 KHM-PCLSFA算法流程本文采用K-调和均值的目标函数KHM(X,C)作为萤火虫i的亮度Ii,并以此确定其移动方向,其本质上是将聚类问题转化为一种优化问题。若k为聚类的数量,m为数据的维数,则用一个k×m列的一维向量x=(x11,x12,…,x1m,…,xk1,xk2,…,xkm)来表示一个聚类中心,即一个萤火虫个体。由于算法对初始值不敏感,可从数据集中随机选择k个不同的点并对其进行较小的扰动以构成一个中心向量x,确定Psize个这样的向量作为种群初始位置。由于本文算法的总迭代次数Itermax较小,不需要执行粗搜索。
综上所述,本文算法KHM-PCLSFA的流程为:
1)初始化算法的基本参数γ、 α、β、Cmax、 N、l并随机初始化萤火虫种群的位置。
2)根据萤火虫的位置计算其目标函数值作为亮度,初始化当前迭代次数gen=0。
3)执行PCLSFA进行搜索,迭代运行gen1次,求出当前的最优个体Gbest以及对应的最优目标函数值Fg,进入下一步操作。并且,选出占种群比例为nc%的最差个体并采用混沌重构法将其替换。
4)以Gbest为聚类中心执行KHM操作,迭代运行gen2次,得到目标函数值KHM(X,C)和聚类中心并将其转化为一维向量xKHM,若KHM(X,C) < Fg,则用xKHM代替Gbest,并以xKHM随机替换一个萤火虫。
5)gen=gen+1,若gen < Itermax,则转到3)继续执行,否则停止迭代得出聚类结果。
若数据集中有n个数据,则KHM每次迭代的时间复杂度为O(knm),本文聚类算法FA部分采用的是同步的适应度更新方式[15],故3)中PCLSFA的时间复杂度为O(gen1•(Psize•(Psize+knm)+Cmax•N•knm)),4)中KHM的时间复杂度为O(gen2•knm),并且Psize < knm,gen2 < gen1•Psize,因此本文算法的时间复杂度为O(Itermax•gen1•(Psize+Cmax•N)•knm)。
3 实验数据与分析 3.1 PCLSFA的性能测试Ackley(xi∈[-30, 30])、Rosenbrock(xi∈[-2.048,2.048])、Rastrigin(xi∈[-5.12,5.12])、Griewank(xi∈[-600, 600]) 进行仿真测试,它们的最优解都是0。通过FA、采用串行CLS分别改进PSO和FA算法的CLSPSO[9]和CLSFA进行对比分析,以验证PCLSFA的收敛性能及寻优能力。各算法种群规模都为Npop=40,最大迭代数Tmax1=2 000,3种具有CLS机制的算法中取Cmax=10,C=5。考虑FA对不同函数的收敛性能不同,在CLSFA和PCLSFA前期执行粗搜索的迭代数也不相同,对f1和f4取Tmax11=500,对f2取Tmax11=0,对f3取Tmax11=200。CLSPSO中采用线性递减的惯性权重w[9],且wmax=0.9,wmin=0.4,学习因子为c1=c2=1.496。FA型算法中统一设置γ=1,随机步长α随着迭代次数t的增加不断减小为
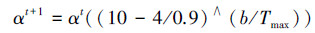
仿真实验基于MATLAB2010b平台,计算机的硬件配置为:Intel Core i5-4 200 M CPU 2.5 GHz、4 GB RAM。各函数的维数均为30,每种算法独立运行30次,计算各自的最大值、最小值、平均值和标准差,记录至表 1。对各函数的收敛曲线为30次运行的平均结果,分别如图 2所示,为了更明显的比较,图中纵坐标是对最优解求lg(f )后的平均值。
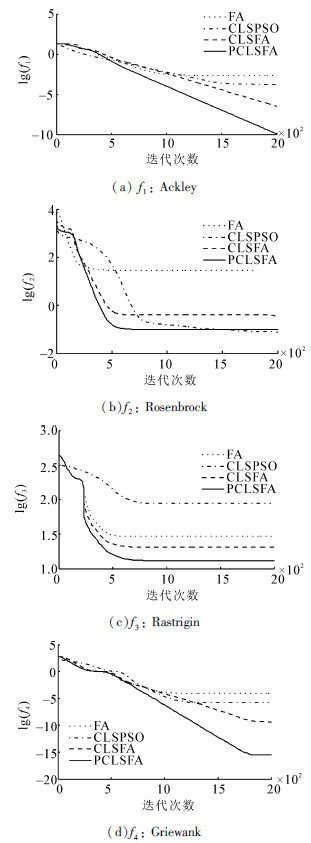 |
| 图 2 各函数的收敛曲线Fig. 2 The convergence curves for test functions |
根据表 1可见,PCLSFA对各函数求出的最优解的平均值及标准差均为最小,表明算法具有较高的寻优精度与稳定性。虽然对f1和f2,CLSPSO能搜索到更佳的最小值,但相应的概率较小,从其偏大的平均值和标准差可以看出。并且,CLSFA对于f1和f4能够获得的最小值与PCLSFA接近,但其很不稳定使其平均值相对较差,有效验证了并行CLS相对于串行CLS的优势。由图 2可见PCLSFA对f1和f4的收敛性均取得了显著的提高,对于相对较难寻优的f2和f3也取得了一定的提高。因此,表 1和图 2中的实验结果有效验证了本文算法的收敛性。尽管PCLSFA对复杂函数的寻优精度方面还有待改进,但是本文中其拥有最好的寻优能力,表明了PCLS机制的引入是有效的。
| 函数 | 算法 | 最小值 | 最大值 | 平均值 | 标准差 |
| f 1 | FA CLSPSO CLSFA PCLSFA |
3.763×10
-4 7.994×10 -15 1.139×10 -10 1.052×10 -10 |
6.981×10
-3 2.660 5 0.052 2 1.496×10 -10 |
3.084×10
-3 1.291 6 0.020 1 1.259×10 -10 |
1.962×10
-3 0.934 4 0.026 0 1.212×10 -11 |
| f 2 | FA CLSPSO CLSFA PCLSFA |
26.575 0 7.919×10 -4 0.030 2 2.208×10 -3 |
29.210 0 4.222 1 32.154 2 0.213 5 |
28.306 0 0.265 1 4.076 0 0.130 8 |
0.804 6 0.717 8 9.609 3 0.066 9 |
| f 3 | FA CLSPSO CLSFA PCLSFA |
20.895 0 59.697 0 10.861 7 6.574 8 |
47.820 0 112.431 0 38.601 4 22.109 1 |
30.911 6 88.551 7 21.039 2 13.212 9 |
7.167 8 12.532 2 5.803 0 4.387 2 |
| f 4 | FA CLSPSO CLSFA PCLSFA |
3.089×10
-5 7.116×10 -14 1.112×10 -16 1.110×10 -16 |
3.441×10
-4 0.048 9 3.296×10 -4 5.541×10 -16 |
1.030×10
-4 9.674×10 -3 9.873×10 -5 3.331×10 -16 |
7.068×10
-5 0.011 7 1.508×10 -4 1.655×10 -16 |
为了验证本文算法的聚类性能,选取了UCI数据库中的6个常用的数据集Iris、Ionosphere、Wine、Image Segmentation(本文简称为Image)、CMC和Satellite进行测试,它们的特性如表 2所示。
| 数据集 | 类数 | 维数 | 数据个数 |
| Iris | 3 | 4 | 150 |
| Ionosphere | 2 | 33 | 351 |
| Wine | 3 | 13 | 178 |
| Image | 7 | 19 | 210 |
| CMC | 3 | 9 | 1473 |
| Satellite | 6 | 33 | 6435 |
本文以目标函数值KHM(X,C)作为聚类的内部评价指标,其值越小则聚类结果越好;F-measure作为聚类的外部评价指标,其值越大则聚类效果越好。若已知类i中的样本数目ni,簇j中的样本数目nj,以及簇j中属于已知类i的样本数目nij,则判准率为p(i,j)=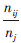 ,查全率为r(i,j)=
,查全率为r(i,j)=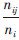 ,样本数为n的数据集的总体F-measure值为
,样本数为n的数据集的总体F-measure值为
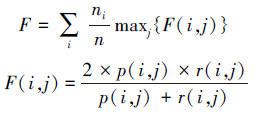
分别采用KHM、KHM-FA、KHM-PSO[3]和本文的KHM-PCLSFA对几种数据集进行实验,其中KHM-FA与文本算法的不同体现在2.1节的3)中执行的是FA。各算法参数设置为:种群规模与文献[3]保持一致Psize=18;KHM的最大迭代次数Maxgen=100,且在迭代过程中若目标函数值不再变化则停止;3种混合聚类算法各部分迭代次数统一设置为Itermax=5,gen1=8,gen2=10。KHM-PSO中PSO的相关参数为w=0.729 8,c1=c2=1.496,FA及PCLSFA的相关参数为γ=1,α=0.1,β同式(17)。这里为了控制PCLS的执行时间,取Cmax=4,N=6,C=3,lPCLS=0.1l。本文分别取p=2.5、3、3.5时对聚类结果进行比较,每种算法独立运行20次,计算各自的KHM(X,C)、F-measure和运行时间的平均值,并分别记录在表 3~表 5中,需注意其中数据集Ionosphere用Sphere表示。从表 3~5可以看出对不同特性的数据集,3种混合聚类算法所得的KHM(X,C)和F-measure值相对于KHM算法均得到了一定的改善。从KHM(X,C)值的降低看出,Iris和Ionosphere在p=3.5时最大程度均降低了0.56%;Wine在p=3.5时最大程度降低了47.77%;Image在p=3.5时最大程度降低了78.91%;CMC在p=3时最大程度降低了0.13%;Satellite在p=3.5时最大程度降低了0.28%。从F-measure值的提升可以看出,Wine在p=3时最大程度提高了5.79%;Image在p=3时最大程度提高了1.63%;CMC在p=3.5时最大程度提高了1.10%;Satellite在p=3时最大程度提高了2.23%。对于Iris和Ionosphere,3种混合算法的F-measure难以获得提高,这里主要通过KHM(X,C)值的降低看出3种混合聚类算法的性能改善,其中本文算法能够获得最小的值,表现出更好的寻优能力。对于Wine和Satellite,几种混合聚类算法的F-measure均取得比较明显的提高。虽然对于CMC和Image的F-measure提高有时比较有限,但是对KHM(X,C)的降低取得了不错的效果,尤其是对于Image,比如在p=2.5时发现KHM算法总是会早熟收敛于KHM(X,C)=9.636 4×107左右的状态,而实验中算法可获得的实际最优值在2.232 6×107左右,这时使得其最终的均值较大,而3种混合算法能够有效减少陷入局部最优的次数,可以看出其均值都有较大程度的降低。
| 数据集 | 算法 | KHM(X,C) | F-measure | 时间/s |
| Iris | KHM KHM-FA KHM-PSO 本文算法 |
148.91 148.84 148.89 148.83 |
0.885 0.885 0.885 0.886 |
0.176 1.322 1.227 2.236 |
| Sphere | KHM KHM-FA KHM-PSO 本文算法 |
2 805.6 2 804.8 2 805.2 2 803.7 |
0.706 0.706 0.706 0.706 |
0.691 5.108 5.105 9.668 |
| Wine | KHM KHM-FAK HM-PSO 本文算法 |
75 338 585.3 75 336 750.4 75 336 842.8 75 335 247.3 |
0.689 0.704 0.701 0.707 |
0.272 2.185 2.216 3.854 |
| Image | KHM KHM-FA KHM-PSO 本文算法 |
54 906 284.3 40 937 350.7 40 178 361.8 29 926 352.6 |
0.595 0.597 0.597 0.599 |
0.921 6.658 6.883 12.034 |
| CMC | KHM KHM-FA KHM-PSO 本文算法 |
96 201.47 96 165.23 96 185.28 96 160.39 |
0.465 0.465 0.464 0.465 |
1.987 14.814 14.924 26.683 |
| Satellite | KHM KHM-FA KHM-PSO 本文算法 |
1.954 3×10
8 1.953 6×10 8 1.953 7×10 8 1.953 3×10 8 |
0.762 0.775 0.771 0.772 |
12.462 92.112 99.459 175.71 |
| 数据集 | 算法 | KHM(X,C) | F-measure | 时间/s |
| Iris | KHM KHM-FA KHM-PSO 本文算法 |
126.08 125.86 125.99 125.81 |
0.892 0.892 0.892 0.893 |
0.181 1.296 1.198 2.195 |
| Sphere | KHM KHM-FA KHM-PSO 本文算法 |
2648.0 2643.5 2646.5 2642.3 |
0.700 0.700 0.700 0.700 |
0.693 5.087 5.067 9.630 |
| Wine | KHM KHM-FA KHM-PSO 本文算法 |
1.049 1×10
9 1.049 1×10 9 1.049 0×10 9 1.049 1×10 9 |
0.622 0.656 0.632 0.658 |
0.262 2.193 2.136 3.831 |
| Image | KHM KHM-FA KHM-PSO 本文算法 |
1.790 6×10
8 1.783 5×10 8 1.788 4×10 8 1.771 3×10 8 |
0.551 0.560 0.559 0.560 |
0.876 6.592 6.703 12.210 |
| CMC | KHM KHM-FA KHM-PSO 本文算法 |
187 018.21 186 824.39 186 943.89 186 778.24 |
0.458 0.461 0.460 0.464 |
1.937 14.885 14.869 26.389 |
| Satellite | KHM KHM-FA KHM-PSO 本文算法 |
8.805 4×10
8 8.802 7×10 8 8.802 8×10 8 8.796 5×10 8 |
0.763 0.776 0.774 0.780 |
12.428 91.250 99.784 175.18 |
| 数据集 | 算法 | KHM(X,C) | F-measure | 时间/s |
| Iris | KHM KHM-FA KHM-PSO 本文算法 |
109.84 109.53 109.61 109.22 |
0.892 0.892 0.892 0.892 |
0.178 1.304 1.235 2.311 |
| Sphere | KHM KHM-FA KHM-PSO 本文算法 |
2 567.9 2 558.9 2 564.4 2 553.5 |
0.700 0.700 0.700 0.700 |
0.684 5.096 5.088 9.662 |
| Wine | KHM KHM-FA KHM-PSO 本文算法 |
2.717 5×10
10 1.420 4×10 10 1.441 9×10 10 1.419 3×10 10 |
0.630 0.655 0.636 0.661 |
0.273 2.201 2.140 3.945 |
| Image | KHM KHM-FA KHM-PSO 本文算法 |
7.089 9×10
9 2.324 2×10 9 1.668 5×10 9 1.494 6×10 9 |
0.535 0.537 0.538 0.540 |
0.928 6.667 6.843 12.162 |
| CMC | KHM KHM-FA KHM-PSO 本文算法 |
380 733.23 380 013.07 380 381.58 379 782.74 |
0.455 0.458 0.458 0.460 |
1.966 14.892 14.855 26.632 |
| Satellite | KHM KHM-FA KHM-PSO 本文算法 |
4.171 4×10
9 4.163 0×10 9 4.150 6×10 9 4.159 7×10 9 |
0.715 0.721 0.709 0.724 |
12.437 92.174 97.873 175.75 |
此外,对于Satellite在p=3.5时,KHMPSO的目标函数值为最小,而其Fmeasure值却低于其他聚类算法,其中的原因值得进一步研究。经过综合对比分析,比较不同p值下的聚类结果可以看出,本文算法在总体上具有最佳的聚类准确性和稳定性,并且对于较复杂数据的改进效果更明显,能够有效避免陷入局部最优解。3种混合聚类算法中都引入了群智能算法的搜索过程,因此它们的运行时间大于KHM,并且本文算法中又引入了PCLS策略,使得其运行时间更长一些,这无法满足于数据规模非常大的聚类问题。在时间效率要求不是很高时适当增加PCLSFA的搜索次数能够进一步获得更佳的结果,并且在很多情况下算法精度方面的要求也显得更为重要。
4 结束语由于传统的KHM算法具有易陷于局部最优解的问题,本文基于一种高效的群智能优化算法提出了一种混合的聚类算法,在KHM中融合了混沌优化改进的萤火虫算法,不断优化其聚类中心。实验结果表明,本文算法的综合性能优于KHM以及2种混合聚类算法KHM-FA和KHM-PSO,具有更高的聚类准确性和稳定性,能够有效地避免陷入局部最优。但是本文算法的运行时间相对比较长,在数据量较大的情况下具有较大的计算开销而影响了算法的效率,接下来可以针对算法效率的改善开展进一步研究工作。此外,可以尝试将PCLSFA应用于其他的优化问题中。
| [1] | JAIN A K. Data clustering:50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8):651-666. |
| [2] | ZHANG Bin, HSU M, DAYAL U. K-harmonic means-a data clustering algorithm. Technical Report HPL-1999-124[R]. Hewlett-Packard Laboratories, 1999. |
| [3] | YANG Fengqin, SUN Tieli, ZHANG Changhai. An efficient hybrid data clustering method based on K-harmonic means and particle swarm optimization[J]. Expert Systems with Applications, 2009, 36(6):9847-9852. |
| [4] | ALGUWAIZANI A, HANSEN P, MLADENOVIC N, et al. Variable neighborhood search for harmonic means clustering[J]. Applied Mathematical Modelling, 2011, 35(6):2688-2694. |
| [5] | HUNG C H, CHIOU H M, YANG Weining. Candidate groups search for K-harmonic means data clustering[J]. Applied Mathematical Modelling, 2013, 37(24):10123-10128. |
| [6] | 汪中, 刘贵全, 陈恩红. 基于模糊K-harmonic means的谱聚类算法[J]. 智能系统学报, 2009, 4(2):95-99. WANG Zhong, LIU Guiquan, CHEN Enhong. A spectral clustering algorithm based on fuzzy K-harmonic means[J]. CAAI Transactions on Intelligent Systems, 2009, 4(2):95-99. |
| [7] | WU Xiaohong, WU Bin, SUN Jun, et al. A hybrid fuzzy K-harmonic means clustering algorithm[J]. Applied Mathematical Modelling, 2015, 39(12):3398-3409. |
| [8] | 王建峰, 孙超, 姜守达. 基于粒子群优化的组合测试数据生成算法[J]. 哈尔滨工程大学学报, 2013, 34(4):477-482.WANG Jianfeng, SUN Chao, JIANG Shouda. Improved algorithm for combinatorial test data generation based on particle swarm optimization[J]. Journal of Harbin Engineering University, 2013, 34(4):477-482. |
| [9] | HE Yaoyao, YANG Shanlin, XU Qifa. Short-term cascaded hydroelectric system scheduling based on chaotic particle swarm optimization using improved logistic map[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7):1746-1756. |
| [10] | HE Yaoyao, XU Qifa, YANG Shanlin, et al. A novel chaotic differential evolution algorithm for short-term cascaded hydroelectric system scheduling[J]. International Journal of Electrical Power & Energy Systems, 2014, 61:455-462. |
| [11] | 廖煜雷, 刘鹏, 王建, 等. 基于改进人工鱼群算法的无人艇控制参数优化[J]. 哈尔滨工程大学学报, 2014, 35(7):800-806.LIAO Yulei, LIU Peng, WANG Jian, et al. Control parameter optimization for the unmanned surface vehicle with the improved artificial fish swarm algorithm[J]. Journal of Harbin Engineering University, 2014, 35(7):800-806. |
| [12] | YANG Xinshe. Firefly algorithm, stochastic test functions and design optimisation[J]. International Journal of Bio-Inspired Computation, 2010, 2(2):78-84. |
| [13] | 赵玉新, YANG X S, 刘利强. 新兴元启发式优化方法[M]. 北京:科学出版社, 2013:148-157. |
| [14] | SENTHILNATH J, OMKAR S N, MANI V. Clustering using firefly algorithm:performance study[J]. Swarm and Evolutionary Computation, 2011, 1(3):164-171. |
| [15] | FISTER Jr I, PERC M, KAMAL S M. A review of chaos-based firefly algorithms:perspectives and research challenges[J]. Applied Mathematics and Computation, 2015, 252:155-165. |
| [16] | GANDOMI A H, YANG X S, TALATAHARI S, et al. Firefly algorithm with chaos[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(1):89-98. |
| [17] | YUAN Xiaofang, ZHAO Jingyi, YANG Yimin, et al. Hybrid parallel chaos optimization algorithm with harmony search algorithm[J]. Applied Soft Computing, 2014, 17:12-22. |
| [18] | YUAN Xiaofang, ZHANG Ting, XIANG Yongzhong, et al. Parallel chaos optimization algorithm with migration and merging operation[J]. Applied Soft Computing, 2015, 35:591-604. |
| [19] | YANG Dixiong, LIU Zhenjun, ZHOU Jilei. Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(4):1229-1246. |
| [20] | 莫愿斌, 马彦追, 郑巧燕, 等. 单纯形法的改进萤火虫算法及其在非线性方程组求解中的应用[J]. 智能系统学报, 2014, 9(6):747-755. MO Yuanbin, MA Yanzhui, ZHENG Qiaoyan, et al. Improved firefly algorithm based on simplex method and its application in solving non-linear equation groups[J]. CAAI Transactions on Intelligent Systems, 2014, 9(6):747-755. |



