,
,
,
2. 江南大学智能系统与网络计算研究所, 江苏无锡 214122
,
,
,
2. Institute of Intelligence System & Network Computing, Jiangnan University, Wuxi 214122, China
Molodtsov等[1]于1999年提出了软集的概念，从参数化的角度研究不确定性问题。由于软集理论参数设置的无约束性以及它与模糊集[2]、粗糙集[3]、直觉模糊集[4]很强的互补性，因此受到学术界的广泛关注，其研究工作也得到迅速开展，并且软集理论已成功运用到信息等诸多领域。2003年，P.K.Maji等先给出详细的软集的软集理论[5]，之后又给出了软集在决策中的应用[6]，2009年，Ali等[7]提出软集一些新的运算。 近年来，软集与代数结构的交融也取得重大进展。 2007年，AktaŞ等[8]给出了软群的新概念，并且刻画出其相关性质，开创了软集代数研究的新领域。 2008年，Jun等[9]将软集运用到BCI/BCK代数中，提出软BCI/BCK代数和软BCI/BCK子代数的概念。2010年，Acar等[10]给出了软环的定义，并对软环的软理想和软同态等相关性质进行了研究；Feng等[11]将软集理论运用到半环上，给出了软半环、软半环的软理想等概念；伏文清等[12]研究了BCK-代数，并给出软BCK-代数的广义交和广义并运算，2012年廖祖华等[14]给出了软坡的概念，并研究了它的一些相关性质。这些工作丰富了软集代数的成果。
域的理论追溯到欧拉、费尔马和高斯。域的一般理论的工作主要从伽罗瓦开始。 1881年，Kronecker提出了有理域的概念。1893年，Heinrich 给出了抽象域的概念。1910年，Steinitz给出域的代数理论。域论在信息加密和编码等计算机领域有广泛的应用。
2008年，温永川[13]将参数集赋予群的代数结构，提出新型软群的概念，并且获得一系列性质。廖祖华的团队在这方面的研究中已得出一系列结果，他们研究了软坡、软群、新型软子群、软子半群、半群的软理想和软完全素理想以及软完全正则子半群，并得到了它们的相关性质[14, 15, 16, 17, 18, 19, 20, 21]。利用这种思想方法将参数集赋予域的代数结构给出新型软域的概念，并研究其相关性质。
1 预备知识定义1[22] 设F是一些元素组成的集合，它有一个乘法运算和一个加法运算。如果F满足下列条件，则F叫做一个域：
1)①加法结合律：(a+b)+c=a+(b+c)；
②加法交换律：a+b=b+a；
③零元素存在：在F中存在一个零元素0，对于任意元素a，a+0=a；
④负元素存在：对于F的任意元素a，在F中存在a的一个负元素-a满足a+(-a)=0。
2)F至少含有2个元素。
3)①乘法结合律(a·b)·c=a·(b·c)；
②乘法交换律a·b=b·a；
③单位元素存在，在F中存在一个单位元素1且1≠0 对于任意元素a，a·1=a；
④逆元素存在，对于F的任意非零元素a，在F中存在a的一个逆元素a-1满足a·a-1=1。
4)乘法对加法的分配律 a·(b+c)=a·b+a·c。
定义2[22] 设F是一个域，F1⊆F。如果F1对F的加法和乘法仍然构成一个域，那么F1叫做F的一个子域。
定理1 设F是一个域，F1⊆F且F1≥2 (F1表示F1中的元素个数)，则F1为F的子域的充要条件是∀x,y∈F1，若满足下列条件：
1)x-y∈F1；
2)当y≠0，xy-1∈F1。
定义3[1] 软集。设U是一个初始集合，E是一个参数集，A⊆E，P(U)表示U的幂集(此后不再说明P(U)的意义)，若F为A到P(U)的映射，则称(F,A)为U上的软集，也称F为A的软集。
定义4[5] 软集的限制交。(F,A)、(G,B)是U上的软集，若软集(H,C)满足：
1)C=A∩B；
2)∀x∈C有H(x)=F(x)∩G(x)。
则称(H,C)是软集(F,A)和(G,B)的限制交，记作(H,C)=(F,A)∩R(G,B)。
定义5[13] 软集的对偶。设H:E→P(X)，g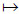
H(g)为一个软集，则称AH:X→P(E),x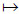AH(x)={g|x∈H(g)}为H的对偶软集。
若A:X→P(E)为一个软集，则HA:E→P(X),g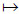HA(g)={x|g∈A(x)}为A的对偶软集。
定义6[23] 设φ是域F到F′的映射。如果映射φ满足：
φ(a+b)=φ(a)+φ(b)
φ(ab)=φ(a)φ(b)
式中：a,b∈F，则称φ是域F到F′的同态映射。当φ为单、满、双射时，分别称为单同态、满同态、同构。同构时记为F=F′，当φ是零映射时，为零同态。 2 新型软域本节将参数集赋予域的代数结构，得到新型软域的概念，并具体探讨它的一系列基本性质。
定义7 设F为一个域，H:F→P(U)为一个软集，若满足
∀x,y∈F，有：
1)H(xy)⊇H(x)∩H(y)；
2)当x≠0时，H(x-1)⊇H(x)；
3)H(x+y)⊇H(x)∩H(y)；
4)H(-x)⊇H(x)。
则称H为F的新型软域，记为(H,F)。在不引起混淆的情况下，简称为软域。
下面的例子说明了新型软域的存在性。
例1 取U=F为剩余类环(Z3,+,·)构成的域，令H([0])=U，H([1])={[1],[2]}，H([2])={[2]}。则由定义知H为F上的新型软子域。但H([1])={[1],[2]}及H([2])={[2]}均不是F的子域。所以它不是通常的软域，因此这是一个新的代数结构。
定理2 设F为一个域，H:F→P(U)为一个软集，H为F的软域的充要条件
∀x,y∈F下列条件成立：
1)当y≠0，H(xy-1)⊇H(x)∩H(y)；
2)H(x-y)⊇H(x)∩H(y)。
证明 1)必要性： ∀x,y∈F。
当y≠0，由定义7中的1)和2)得，H(xy-1)⊇H(x)∩H(y-1)⊇H(x)∩H(y)；由定义7中的3)和4)得，H(x-y)=H[x+(-y)]⊇H(x)∩H(-y)⊇H(x)∩H(y)。
2)充分性：
∀x∈F且x≠0，则H(1)=H(xx-1)⊇H(x)∩H(x)=H(x)。
∀x∈F，则H(0)=H(x-x)⊇H(x)∩H(x)=H(x)。
∀x≠0∈F，由H(x-1)=H(1x-1)⊇H(1)∩H(x)=H(x)，因此定义7的2)成立。
∀x,y∈F，当y≠0时，H(xy)=H[x(y-1)-1]⊇H(x)∩H(y-1)⊇H(x)∩H(y)；当y=0时，H(xy)=H(0)⊇H(x)∩H(y)。因此定义7的1)成立。
∀x∈F，由H(-x)=H(0-x)⊇H(0)∩H(x)⊇H(x)，因此定义7的3)成立。
∀x,y∈F，由H(x+y)=H[x-(-y)]⊇H(x)∩H(-y)⊇H(x)∩H(y)，因此定义7的4) 成立。
综上所述，H为F的软域。
定理3 设F1、F2是域F上的2个子域，H1、H2分别是F1、F2的软域，F1∩F2≠∅，(H,F1∩F2)=(H1,F1)∩R(H2,F2)，则H是F1∩F2的软域。
证明 F1、F2域F的2个子域，则F1∩F2也是域。又∀x,y∈F1∩F2，当y≠0时，H(xy-1)=H1(xy-1)∩H2(xy-1)⊇[H1(x)∩H1(y)]∩[H2(x)∩H2(y)]=[H1(x)∩H2(x)]∩[H1(y)∩H2(y)]=H(x)∩H(y)；
H(x-y)=H1(x-y)∩H2(x-y)⊇[H1(x)∩H1(y)]∩[H2(x)∩H2(y)]=[H1(x)∩H2(x)]∩[H1(y)∩H2(y)]=H(x)∩H(y)。综上所述，H是F1∩F2的软域。
定理4 设F为域，则
1)H为F的一个软域的充要条件是：∀u∈U，当|AH(u)|=1时，AH(u)={0}；当|AH(u)|≥2时，AH(u)为F的子域。
2)A:U→P(F)，HA为F的一个软域的充要条件是：∀u∈U，当|A(u)|=1时，A(u)={0}；当|A(u)|≥2时，A(u)为F的一个子域。
证明 先证明定理4的1)成立。
必要性：若H为F的一个软域，∀u∈U。
1)当|AH(u)|=1时，若x∈AH(u)，则u∈H(x)。由H为F的一个软域，所以H(x2)=H(xx)⊇H(x)∩H(x)=H(x)，因此u∈H(x2)，则x2∈AH(u)。因|AH(u)|=1，所以x2=x。又因为F是一个域，所以x=0或者x=1。若x=1，由H为F的一个软域，则H(1+1)⊇H(1)∩H(1)=H(1)。所以u∈H(1+1)。因此1+1∈AH(u)。因为|AH(u)|=1，所以1+1=1。得到1=0。此为矛盾。因此x≠1。故x=0，因此AH(u)={0}。
2)当|AH(u)|≥2时，∀x,y∈AH(u)，得到u∈H(x)且u∈H(y)，所以u∈H(x)∩H(y)。由H为F的一个软域，则u∈H(x)∩H(y)⊆H(x-y)，所以u∈H(x-y)，因此x-y∈AH(u)；当y≠0时，又由H为F的一个软域，从而u∈H(x)∩H(y)⊆H(xy-1)，故u∈H(xy-1)，因此xy-1∈AH(u)。综上所述，根据定理1知AH(u)为F的子域。
充分性：
1)∀x,y∈F，∀u∈H(x)∩H(y)，则u∈H(x)且u∈H(y)，因此x∈AH(u)且y∈AH(u)。当|AH(u)|=1时，由已知AH(u)={0}，因此x=y=0，所以H(xy)=H(00)=H(0)⊇H(0)=H(x)∩H(y)；当|AH(u)|≥2时，由AH(u)为F的子域，则xy∈AH(u)，所以u∈H(xy)，因此H(xy)⊇H(x)∩H(y)。综上所述，H(xy)⊇H(x)∩H(y)。
2)∀x∈F且x≠0，∀u∈H(x)，因此x∈AH(u)。若|AH(u)|=1，由已知AH(u)={0}，所以x=0与x≠0矛盾。 因此|AH(u)|≥2，由已知AH(u)为F的子域，则x-1∈AH(u)，所以u∈H(x-1)，因此H(x-1)⊇H(x)。综上所述，H(x-1)⊇H(x)。
3)∀x,y∈F，∀u∈H(x)∩H(y)，则u∈H(x)且u∈H(y)，因此x∈AH(u)且y∈AH(u)。当|AH(u)|=1时，由已知AH(u)={0}，因此x=y=0，所以H(x+y)=H(0+0)=H(0)⊇H(0)=H(x)∩H(y)；当|AH(u)|≥2时，由已知AH(u)为F的子域，则x+y∈AH(u)，所以u∈H(x+y)，因此H(x+y)⊇H(x)∩H(y)。综上所述，H(x+y)⊇H(x)∩H(y)。
4)∀x∈F，∀u∈H(x)，则x∈AH(u)。当|AH(u)|=1时，由已知AH(u)={0}，所以H(-x)=H(-0)=H(0)⊇H(0)=H(x)。当|AH(u)|2时，由已知AH(u)为F的子域，则-x∈AH(u)，所以u∈H(-x)，因此H(-x)⊇H(x)。综上所述，H(-x)⊇H(x)。
综合1)~4)，由定义7知H为F的一个软域。
其次证明定理4的2)成立。
必要性：若HA为F的一个软域，∀u∈U
1)当A(u)=1时，若x∈A(u)，则u∈HA(x)。
由HA为F的一个软域，所以HA(x2)=HA(xx)⊇HA(x)∩HA(x)=HA(x)，因此u∈HA(x2)，则x2∈A(u)。因|A(u)|=1，所以x2=x。又因为F是一个域，所以x=0或者x=1。若x=1，由HA为F的一个软域，则HA(1+1)⊇HA(1)∩HA(1)=HA(1)。所以u∈HA(1+1)。因此1+1∈A(u)。因|A(u)|=1，所以1+1=1。得到1=0。此为矛盾。因此x≠1。故x=0，因此A(u)={0}。
2)当|A(u)|≥2时，∀x,y∈A(u)得到u∈HA(x),且u∈HA(y)，所以u∈HA(x)∩HA(y)。由HA为F的一个软域，则u∈HA(x)∩HA(y)⊆HA(x-y)，所以u∈HA(x-y)，因此x-y∈A(u)；当y≠0时，又由HA为F的一个软域，从而u∈HA(x)∩HA(y)⊆HA(xy-1) ，故u∈HA(xy-1)，即xy-1∈A(u)。综上所述，根据定理1知A(u)为F的子域。
充分性：
1)∀x,y∈F，∀u∈HA(x)∩HA(y)，则u∈HA(x)且u∈HA(y)，因此x∈A(u)且y∈A(u)。当A(u)=1时，由已知A(u)={0}，因此x=y=0，所以HA(xy)=HA(00)=HA(0)⊇HA(0)=HA(x)∩HA(y)；当A(u)≥2时，由已知A(u)为F的一个子域，则xy∈A(u)，所以u∈HA(xy)，因此HA(xy)⊇HA(x)∩HA(y)。综上所述，HA(xy)⊇HA(x)∩HA(y)。
2)∀x∈F且x≠0，∀u∈HA(x)，因此x∈A(u)。若A(u)=1，由已知A(u)={0}，所以x=0与x≠0矛盾。因此A(u)≥2，由已知A(u)为F的一个子域，则x-1∈A(u)，所以u∈HA(x-1)。因此HA(x-1)⊇HA(x)。综上所述，HA(x-1)⊇HA(x)。
3)∀x,y∈F，∀u∈HA(x)∩HA(y)，则u∈HA(x)且u∈HA(y)，因此x∈A(u)且y∈A(u)。当A(u)=1时，由已知A(u)={0}，因此x=y=0，所以HA(x+y)=HA(0+0)=HA(0)⊇HA(0)=HA(x)∩HA(y)；当A(u)≥2 时，由已知A(u)为F的一个子域，则x+y∈A(u)，所以u∈HA(x+y)，因此HA(x+y)⊇HA(x)∩HA(y)。综上所述，HA(x+y)⊇HA(x)∩HA(y)。
4)∀x∈F，∀u∈HA(x)，则 x∈A(u)。当A(u)=1时，由已知A(u)={0}，所以HA(-x)=HA(-0)=HA(0)⊇HA(0)=HA(x)；当A(u)≥2时，由已知A(u)为F的一个子域，则-x∈A(u)，所以u∈HA(-x)。因此HA(-x)⊇HA(x)。综上所述，HA(-x)⊇HA(x)。
综合1)~4)，由定义7知HA为F的一个软域。
3 新型软域的像与原像本节给出新型软域像与原像的基本概念及相关性质。
定义8 设F1、F2为2个域，U是初始集合。
f:F1→F2为一个映射，H1:F1→P(u)和H2:
F2→P(u)是2个软集，∀x1∈F1,x2∈F2，
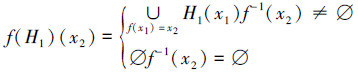
定理5 设f是域F1到F2的同态映射。则
1)f(0)=0；∀x∈F，f(-x)=-f(x)。
2)f不是零同态，则f(1)=1；∀x∈F且x≠0，则f(x-1)=(f(x))-1。
定理6 设F1、F2为域，U是初始集合，f:F1→F2为一个同态映射，H1:F1→P(u)，H2:
F2→P(u)是2个软集：
1)若H1为F1的软域，则f(H1)为F2的软域。
2)若H2为F2的软域，则f-1(H2)为F1的软域。
证明 先证明定理6的1)成立。
当f是零同态时，
①∀h1,H2∈F2且H2≠0，那么f(H1)(H2)=∅，所以f(H1)(h1)∩f(H1)(H2)=∅⊆f(H1)(h1H2-1)。
②∀h1,H2∈F2，若h1≠0或H2≠0，则f(H1)(h1)=∅或f(H1)(H2)=∅，所以f(H1)(h1)∩f(H1)(H2)=∅⊆f(H1)(h1-H2)；若h1=0且H2=0，则f(H1)(h1)∩f(H1)(H2)=f(H1)(0)∩f(H1)(0)⊆f(H1)(0)=f(H1)(h1-H2)。综合① 、②知f(H1)为F2的软域。
当f不是零同态时
③∀h1,H2∈F2且H2≠0，若f(H1)(h1)=∅或f(H1)(H2)=∅，则f(H1)(h1)∩f(H1)(H2)=∅⊆f(H1)(h1H2-1)；若f(H1)(h1)≠∅且f(H1)(H2)≠∅，则∀u∈f(H1)(h1)∩f(H1)(H2)，有u∈∪f(x)=h1H1(x)且u∈∪f(x)=H2H1(x)，所以∃x1∈F1，使u∈H1(x1)且h1=f(x1)；∃x2∈F1，使u∈H1(x2)且H2=f(x2)，所以u∈H1(x1)∩H1(x2)。 由H1为F1的软域，所以 H1(x1)∩H1(x2)⊆H1(x1x2-1)，所以u∈H1(x1x2-1)。由定理5中2)得，f(x2-1)=(f(x2))-1=H2-1。又因为f为同态映射，所以f(x1x2-1)=f(x1)f(x2-1)=h1H2-1，其中x1x-12∈F1，得u∈∪f(x)=h1H2-1H1(x)=f(H1)(h1H2-1)。所以f(H1)(h1)∩f(H1)(h2)⊆f(H1)(h1h2-1)。
④ ∀h1,H2∈F2，若f(H1)(h1)=∅或f(H1)(H2)=∅，则f(H1)(h1)∩f(H1)(H2)=∅⊆f(H1)(h1-H2)；若f(H1)(h1)≠∅且f(H1)(H2)≠∅，则∀u∈f(H1)(h1)∩f(H1)(H2)，有u∈∪f(x)=h1H1(x)且u∈∪f(x)=H2H1(x)，所以∃x1∈F1，使u∈H1(x1)且h1=f(x1)；∃x2∈F1，使u∈H1(x2)且H2=f(x2)，所以u∈H1(x1)∩H1(x2)。由H1为F1的软域，则H1(x1)∩H1(x2)⊆H1(x1-x2)，所以u∈H1(x1-x2)。因为f为同态映射，再由定理3.1(1)知f(-x2)=-f(x2)=-H2，f(x1-x2)=f(x1+(-x2))=f(x1)+f(-x2)=f(x1)-f(x2)=h1-H2，所以u∈∪f(x)=h1-H2H1(x)=f(H1)(h1-H2)。则f(H1)(h1)∩f(H1)(h2)⊆f(H1)(h1-h2)。
综合③ 、④知f(H1)为F2的软域。
其次证明定理6的(2)成立。
当f是零同态时
①∀g1,g2∈F1且g2≠0，那么f-1(H1)(g2)=∅，所以f-1(H2)(g1)∩f-1(H2)(g2)=H2(f(g1))∩H2(f(g2))=H2(0)∩H2(0)⊆H2(0)=H2(f(g1g2-1))=f-1(H2)(g1g2-1)。
②∀g1,g2∈F1，若g1≠0或g2≠0，则f-1(H2)(g1)=∅或f-1(H2)(g2)=∅，则f-1(H2)(g1)∩f-1(H2)(g2)=∅⊆f-1(H2)(g1-g2)；若g1=0且g2=0，则f-1(H2)(g1)∩f-1(H2)(g2)=H2(f(g1))∩H2(f(g2))=H2(0)∩H2(0)⊆H2(0)=H2(f(g1-g2))=f-1(H2)(g1-g2)。
综合① 、②知f-1(H2)为F1的软域。
当f不是零同态时
③∀g1,g2∈F1且g2≠0，因H2为F2的软域且f为同态映射，所以f-1(H2)(g1)∩f-1(H2)(g2)=H2(f(g1))∩H2(f(g2))⊆H2(f(g1)(f(g2))-1)=H2(f(g1)f(g2-1))=H2(f(g1g2-1))=f-1(H2)(g1g2-1)。
④∀g1,g2∈F1，因H2为F2的软域且f为同态映射，所以f-1(H2)(g1)∩f-1(H2)(g2)=H2(f(g1))∩H2(f(g2))⊆H2(f(g1)-f(g2))=H2(f(g1)+f(-g2))=H2(f(g1-g2))=f-1(H2)(g1-g2)。
综合③ ④知f-1(H2)为F1的软域。
定义9设F1,F2是2个域，f:F1→F2是映射，H1是F1的软域。∀x,y∈F1，f(x)=f(y)，则
H1x=H1y，则称H1是f-不变的。
定理7 设F1、F2是2个域，U是初始集合，f:F1→F2为一个非零同态映射，H1:F1→P(u)为F1上的软集且H1是关于f-不变的。则H1为F1的软域充要条件是f(H1)是F2的软域。
证明 必要性：由定理6(1)可得结论。
充分性：
①∀g1,g2∈F1且g2≠0，令f(g1)=H1，f(g2)=H2所以h1,H2∈F2且H2≠0(由f为非零同态)。若H1(g1)∩H1(g2)=∅，则H1(g1)∩H1(g2)=∅⊆H1(g1)∩H1(g2)=∅⊆H1(g1g2-1)；若H1(g1)∩H1(g2)≠∅，∀x∈H1(g1)∩H1(g2)，则x∈H1(g1)且x∈H1(g2)，x∈∪f(g)=H1H1(g)=f(H1)(H1)且x∈∪f(g)=H2H1(g)=f(H1)(H2)，即x∈f(H1)(H1)∩f(H1)(H2)。由f(H1)是F2的软域，则f(H1)(H1)∩f(H1)(H2)⊆f(H1)(H1H2-1)，故x∈∪f(g)=H1H2-1H1(g)。因为f为非零同态映射，所以 f(g1g2-1)=f(g1)f(g2-1)=f(g1)(f(g2))-1=H1H2-1。因H1是关于f-不变的，则∪f(g)=H1H2-1H1(g)=H1(g1g2-1)，从而x∈H1(g1g2-1)，故H1(g1)∩H1(g2)⊆H1(g1g2-1)。
②∀g1,g2∈F1，令f(g1)=H1，f(g2)=H2，所以H1,H2∈F2。若H1(g1)∩H1(g2)=∅，则H1(g1)∩H1(g2)=∅⊆H1(g1-g2)；若H1(g1)∩H1(g2)≠∅，∀x∈H1(g1)∩H1(g2)，则x∈H1(g1)且x∈H1(g2)，x∈∪f(g)=H1H1(g)=f(H1)(H1)且x∈∪f(g)=H2H1(g)=f(H1)(H2)，即x∈f(H1)(H1)∩f(H1)(H2)。由f(H1)是F2的软域，则f(H1)(H1)∩f(H1)(H2)⊆f(H1)(H1-H2)故x∈∪f(g)=H1-H2H1(g)，因为f为同态映射，所以f(g1-g2)=f(g1)-f(g2)=H1-H2。因H1是关于f-不变的，则∪f(g)=H1-H2H1(g)=H1(g1-g2)，从而x∈H1(g1-g2)，故H1(g1)∩H1(g2)⊆H1(g1-g2)。
综合① 、②知H1为F1的软域。
定理8 设F1与F2是2个域，f:F1→F2为域的满同态映射，H2:F2→P(u)为F2上的软集。则H2为F2的软域的充要条件是f-1(H2)是F1的软域。
证明 必要性 由定理6中的2)可得结论。
充分性：
①∀H1,H2∈F2且H2≠0，因为f是满射，所以存在g1,g2∈F1且g2≠0，使得H1=f(g1)，H2=f(g2)。
又因f-1(H2)是F1的软域且f是同态映射，所以H2(H1)∩H2(H2)=H2(f(g1))∩H2(f(g2))=f-1(g1)∩f-1(H2)(g2)⊆f-1(H2)(g1g2-1)=H2(f(g1g2-1))=H2(f(g1)f(g2-1))=H2(H1h2-1)，即H2(H1)∩H2(h2)⊆H2(H1h2-1)。
②∀H1,H2∈F2，因为f是满射，所以存在g1,g2∈F1，使得H1=f(g1)，H2=f(g2)，因为f-1(H2)是F1的软域且f是同态映射，所以H2(H1)∩H2(H2)=H2(f(g1))∩H2(f(g2))=f-1(H2)(g1)∩f-1(H2)(g2)⊆f-1(H2)(g1-g2)=H2(f(g1-g2))=H2(f(g1)-f(g2))=H2(H1-h2)，即H2(H1)∩H2(h2)⊆H2(H1-h2)。
综合① 、②知H2为F2的软域。
4 结束语软集是国内外众多学者关注的研究课题。本文将参数集赋予域代数结构，给出了新型软域的代数结构，并讨论了它的一系列代数性质。进一步的工作将新型软域与模糊集理论相结合，提出新型模糊软域的代数结构，探讨它们的相关性质。
| [1] | MOLODTSOV D. Soft set theory-first results[J]. Computers & Mathematics with Applications, 1999, 37(4/5):19-31. |
| [2] | ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3):338-353. |
| [3] | PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5):341-356. |
| [4] | ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1):87-96. |
| [5] | MAJI P K, BISWAS R, ROY A R. Soft set theory[J]. Computers & Mathematics with Applications, 2003, 45(4-5):555-562. |
| [6] | MAJI P K, ROY A R. An application of soft sets in a decision making problem[J]. Computers & Mathematics with Applications, 2002, 44(8/9):1077-1083. |
| [7] | ALI M I, FENG Feng, LIU Xiaoyan, et al. On some new operations in soft set theory[J]. Computers & Mathematics with Applications, 2009, 57(9):1547-1553. |
| [8] | AKTAş H, çAĜMAN N. Soft sets and soft groups[J]. Information Sciences, 2007, 177(13):2726-2735. |
| [9] | JUN Y B. Soft BCK/BCI-algebras[J]. Computers & Mathematics with Applications, 2008, 56(5):1408-1413. |
| [10] | ACAR U, KOYUNCU F, TANAY B. Soft sets and soft rings[J]. Computers & Mathematics with Applications, 2010, 59(11):3458-3463. |
| [11] | FENG Feng, JUN Y B, ZHAO Xianzhong. Soft semirings[J]. Computers & Mathematics with Applications, 2008, 56(10):2621-2628. |
| [12] | 伏文清, 李生刚. 软BCK代数[J]. 计算机工程与应用, 2010, 46(10):5-6. FU Wenqing, LI Shenggang. Soft BCK algebra[J]. Computer Engineering and Applications, 2010, 46(10):5-6. |
| [13] | 温永川. 关于软集的研究[D]. 大连:辽宁师范大学, 2008:18-19. WEN Yongchuan. The study on soft set[D]. Dalian:Liaoning Normal University, 2008:18-19. |
| [14] | 廖祖华, 芮眀力. 软坡[J]. 计算机工程与应用, 2012, 48(2):30-32. LIAO Zuhua, RUI Mingli. Soft inclines[J]. Computer Engineering and Applications, 2012, 48(2), 30-32. |
| [15] | 殷霞, 廖祖华, 朱晓英, 等. 软集与新型软子群[J]. 计算机工程与应用, 2012, 48(33):40-43, 62. YIN Xia, LIAO Zuhua, ZHU Xiaoying, et al. Soft sets and new soft subgroups[J]. Computer Engineering and Applications, 2012, 48(33):40-43, 62. |
| [16] | YIN Xia, LIAO Zuhua. Study on soft groups[J]. Journal of Computers, 2013, 8(4):960-967. |
| [17] | ZHENG Gaoping, LIAO Zuhua, WANG Nini, et al. Soft lattice implication subalgebras[J]. Applied Mathematics and Information Sciences, 2013, 7(3):1181-1186. |
| [18] | 关贝贝, 廖祖华, 朱晓英, 等. 软子半群[J]. 模糊系统与数学, 2014, 28(4):39-44. GUAN Beibei, LIAO Zuhua, ZHU Xiaoying, et al. Soft subsemigroups[J]. Fuzzy Systems and Mathematics, 2014, 28(4):39-44. |
| [19] | 赵迪, 廖祖华, 朱晓英, 等. 半群的软理想[J]. 模糊系统与数学, 2014, 28(4):45-50. ZHAO Di, LIAO Zuhua, ZHU Xiaoying, et al. Soft ideals of semigroups[J]. Fuzzy Systems and Mathematics, 2014, 28(4):45-50. |
| [20] | 叶婷, 廖祖华, 朱晓英, 等. 半群的软完全素理想[J]. 模糊系统与数学, 2014, 28(3):27-31. YE Ting, LIAO Zihua, ZHU Xiaoying, et al. Soft completely prime ideals of semigroups[J]. Fuzzy Systems and Mathematics, 2014, 28(3):27-31. |
| [21] | 叶灵军, 廖祖华, 朱晓英, 等. 软完全正则子半群[J]. 工程数学学报, 2014, 31(3):341-346. YE Lingjun, LIAO Zuhua, ZHU Xiaoying, et al. Soft completely regular sub-semigroups[J]. Chinese Journal of Engineering Mathematics, 2014, 31(3):341-346. |
| [22] | 林东岱. 代数基础与有限域[M]. 北京:高等教育出版社, 2006. |
| [23] | 南基洙. 域和Galois理论[M]. 北京:科学出版社, 2009. |